基于状态变换法的车辆悬架系统时滞反馈控制

闫 盖，方明霞，董天夫，纪仁杰

（同济大学航空航天与力学学院，上海 200092）

0 引 言

车辆乘坐舒适性的提高一直是业内专家学者致力研究的问题，从外部条件分析对车辆振动的影响，到对悬架刚度阻尼参数的最优匹配设计，一定程度上提高了悬架的减振性能[1-5]。近年来，车辆主动/半主动悬架是研究的热点，它主要是根据车辆行驶状况，通过作动器对系统施加控制力，实现车辆行驶平顺性和安全性提高的目的[6-13]，而车辆悬架主动/半主动控制系统中，由于信号采集、传输、控制器计算、作动器作动等因素，固有时滞不可避免，且研究发现时滞对系统控制的影响极大，甚至导致系统失稳发散[14-16]。为了提高控制精度，出现了大量时滞消除补偿技术，文献[17]采用随机预瞄控制策略对车辆主动悬架进行研究，发现即使很小的时滞也可能导致系统控制效率降低，甚至使系统出现不稳定现象；文献[18]采用平均法对含时滞的汽车半主动悬架进行研究，得到系统出现不稳定运动的条件和临界时滞，发现系统稳定性随着时滞会发生周期性变化；文献[19]采用时滞天棚开关控制策略，研究半主动悬架时滞渐进稳定性机理，获得时滞对半主动悬架系统动特性及动态稳定性的影响规律；文献[20]研究了磁流变减振器半主动悬架，测量了磁流变阻尼器的响应时间，以常微分方程理论求得系统临界时滞，并应用Smith预估控制设计时滞补偿控制器，改善了车辆半主动悬架性能；文献[21]通过数值方法研究了时滞对铁道车辆平顺性、稳定性和安全性的影响。文献[22-23]采用离散最优控制和离散变结构控制方法研究多时滞问题，理论和试验结果均表明采用时滞控制律可以有效抑制梁和板的振动。文献[24]发现时滞可以改变饱和控制的有效频带范围，将其作为控制参数可有效抑制系统振动。

由于控制过程中时滞量非常小，对时滞控制系统进行试验验证有较大难度，因此目前时滞消除补偿技术主要采用数值方法进行研究，难以从根本上解决系统稳定性问题，且对于处理大时滞问题具有一定的局限性。为此，本文采用理论与试验相结合的方法对含时滞的半主动悬架系统动力学特性进行研究，分析时滞参数对悬架系统控制稳定性及响应特性的影响，采用状态变换方法设计时滞反馈最优控制器，最后利用试验方法对研究结果的有效性进行验证。

1 车辆悬架系统时滞动力学模型建立及响应分析

1.1 悬架系统时滞动力学模型

车身垂直振动是影响车辆行驶平顺性的主要因素，由于车辆结构复杂，本文研究中忽略车身的俯仰运动和侧倾运动，以赛欧轿车悬架系统为基础，以磁流变阻尼器作为作动器，将系统简化为考虑时滞的 2自由度四分之一悬架半主动控制模型，其简化模型如图1所示。

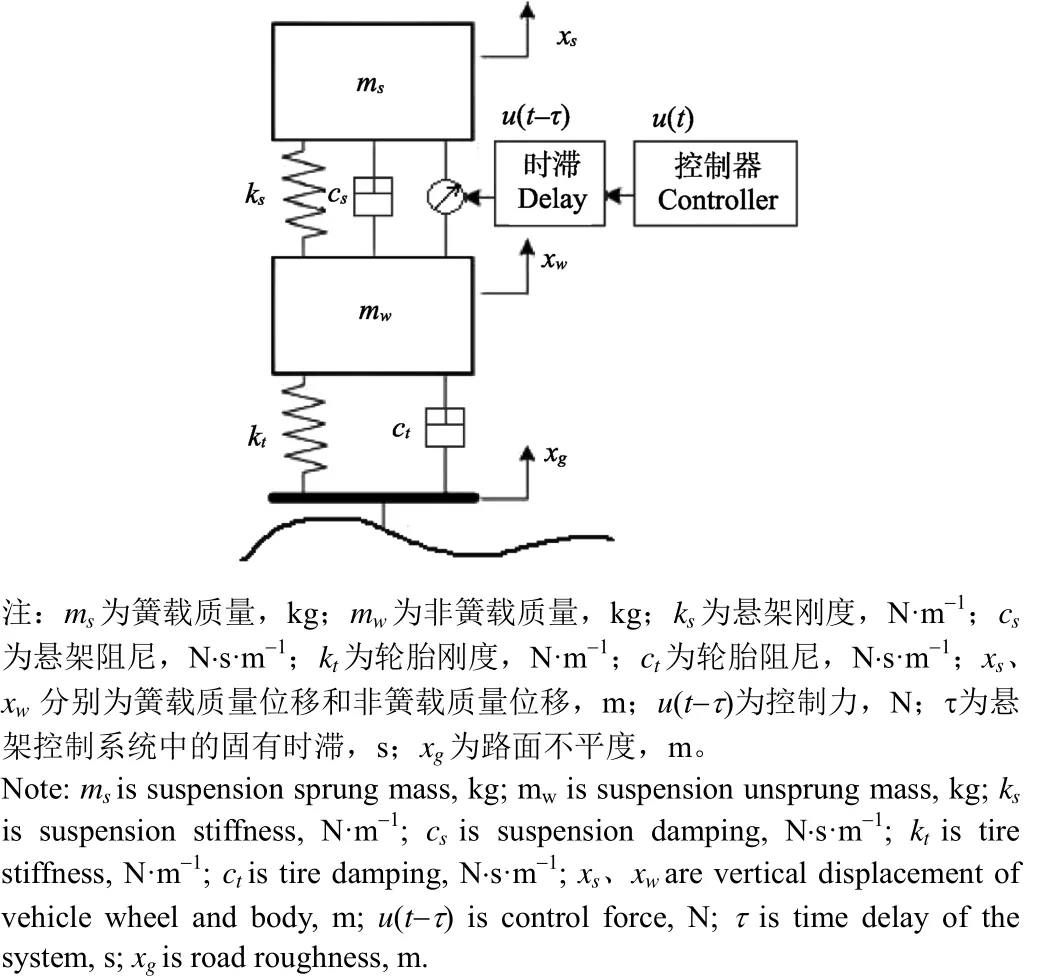
图1 悬架控制系统模型图Fig.1 Suspension control system model

利用第二类拉氏方程，得到悬架系统的动力学方程如下：

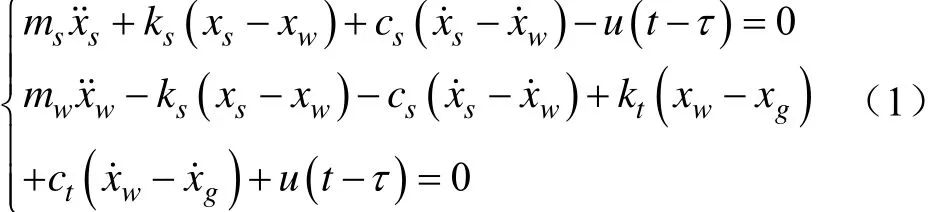
式中 ms为簧载质量； mw为非簧载质量； ks、 cs分别为悬架刚度和阻尼；kt、ct分别为轮胎刚度和阻尼；xs、xw分别为簧载质量位移和非簧载质量位移； u（ t- τ ）为控制力；τ为悬架控制系统中的固有时滞； xg为路面不平度。

选取状态向量为 x = []T，输出量为y=，得到系统的状态方程为:

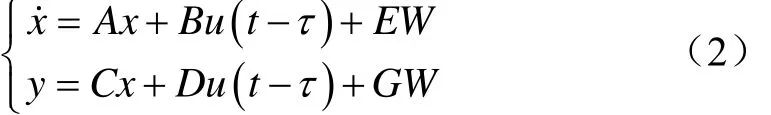
式中

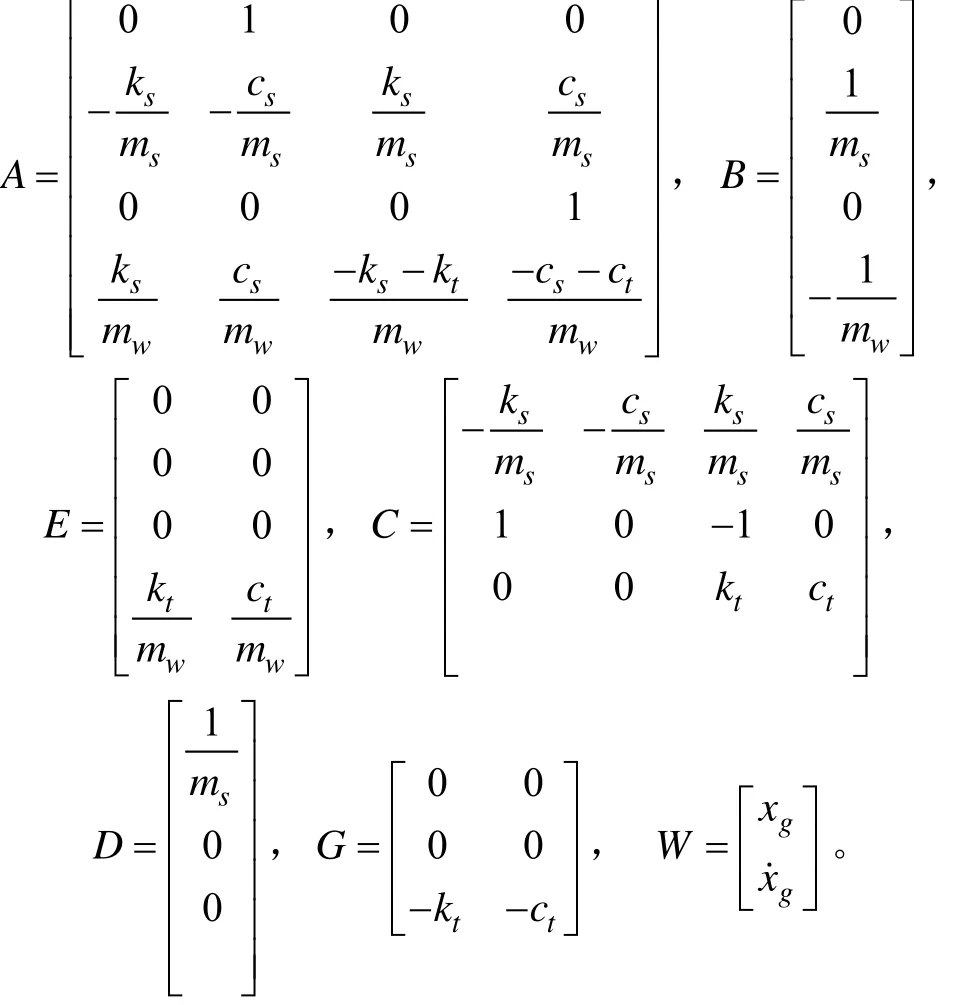
1.2 含时滞悬架系统时域响应分析

悬架系统的控制目标是提高车辆行驶平顺性和操纵稳定性，即尽可能地降低车身垂向振动加速度、轮胎动载荷和悬架动行程性能指标，同时要求实现控制目标的能量最小。因此，根据二次型最优控制方法，取目标函数为：

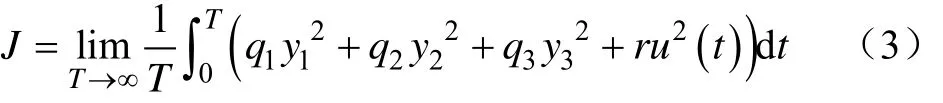
式中 q1、 q2、 q3和r分别为车身垂向振动加速度m/s2、悬架动行程m、轮胎动载荷N和控制力N的加权系数。加权系数的大小表示性能指标在悬架设计中的重要程度，选取时需综合考虑悬架的安全性和舒适性。

在传统二次型最优控制下可得 u（ t） = - K x（ t），参照赛欧轿车悬架系统参数，仿真计算时取悬架系统及控制参数为 ms= 1 36.05kg， mw= 2 4.288kg， ks= 1 0 200N/m，ks= 9 8 000 N/ m ，ct=15 N·s/m， cs=153.11 N· s/m，q1=1000 000,q2=800，q3=70，r= 0 .3，利用matlab/ simulink建立悬架系统仿真模型，在确定性激励 xg= 0 .004sin（2π ft ） 、f= 5 Hz下进行仿真计算。

由于控制过程中时滞量相对较小，本文在0.2 s内任意选取多个时滞量进行仿真计算。为了便于与无控制及后文的试验结果相比较，图2给出了无控制及τ=0、0.010、0.014 3、0.065s时系统的响应结果。为便于观察，图中纵坐标没有取到最大值。

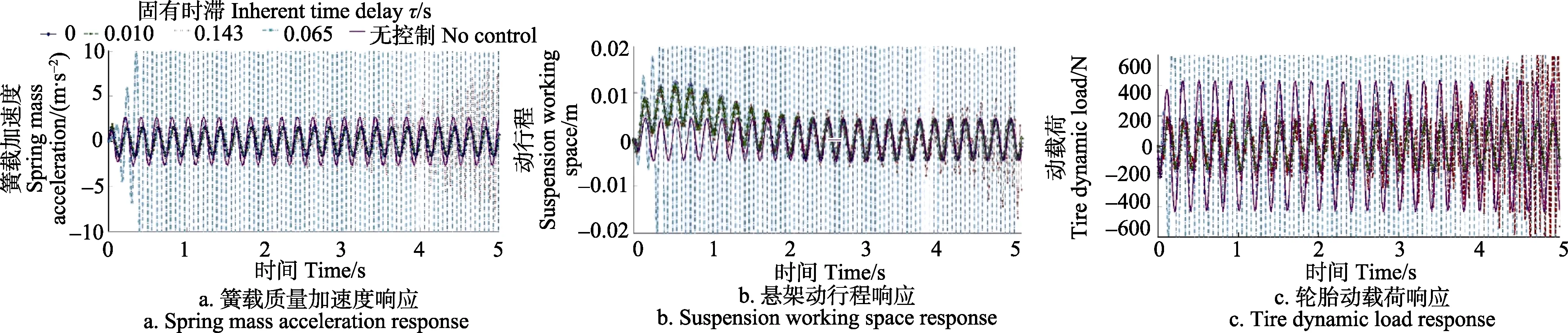
图2 传统二次型最优控制下系统时域响应Fig.2 Response of system under traditional two degree optimal control

从图2可以看出，当τ=0、0.01 s时，簧载质量加速度幅值稳定，分别为1.56、1.92 m/s2，因此传统二次型最优控制可以保持控制系统稳定，相比无控制时簧载质量加速度幅值2.70 m/s2亦有减振效果；但当 τ = 0 .0143s时，簧载质量加速度随时间逐渐增大，5 s时可增加至10 m/s2，而且随着时间增大，加速度继续增大，当τ = 0 .065s时，簧载质量加速度在很短时间内超过了 10 m/s2，5 s可达1017，因此传统二次型最优控制无法保证系统稳定性，导致控制后系统发散，这对系统结构具有极大的损害。因此，在系统控制中必须考虑时滞因素的影响。

2 车辆悬架系统控制稳定性分析

在控制中，信号采集传输、控制计算及作动器作动延迟，时滞因素必然存在，从1.2节仿真结果可知当系统时滞较小时，传统二次型最优控制可以满足控制要求，但当系统时滞较大时，系统可能会失稳发散。事实上，系统时滞稳定性可以通过常微分方程理论进行求解。

2.1 系统时滞稳定区间的理论分析

根据常微分方程理论[25]，方程（1）的特征值为λ时，方程解的形式可表示为

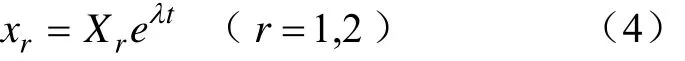
令反馈增益 K =[g1, g2, g3, g4]，则：

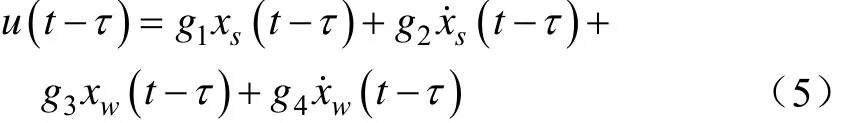
将式（4）、（5）代入式（1），并根据非零解条件可得系统特征方程为：

式中

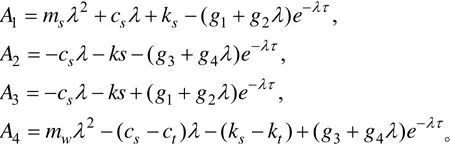
根据李雅普诺夫稳定性判据[26]，系统实现稳定的条件是式（6）所有根均有负实部，因此系统失稳的临界条件是式（6）仅有纯虚根iwλ=，其中w是系统自激振动下的基频。将λ代入式（6），运用欧拉公式分离方程实部和虚部，得到系统仅有纯虚根的条件为：

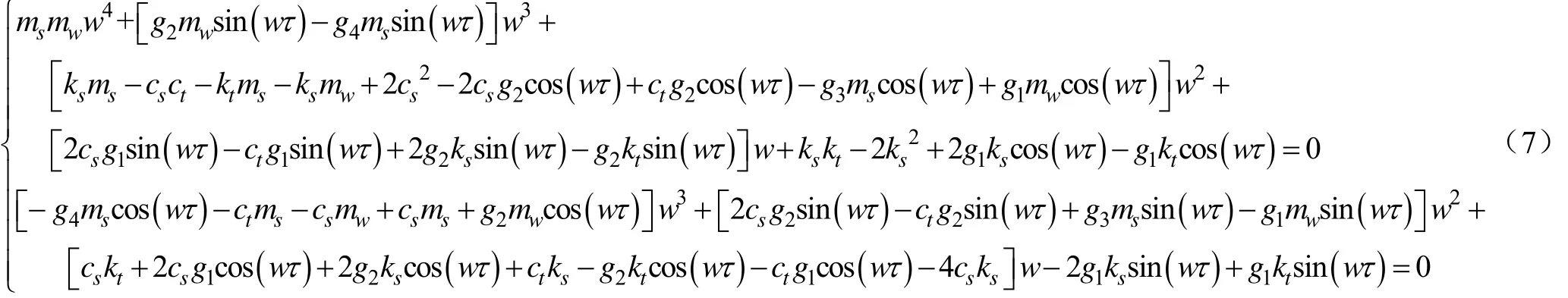
由 s in2（wτ ） + c o s2（wτ）= 1可得到关于w的方程如下：

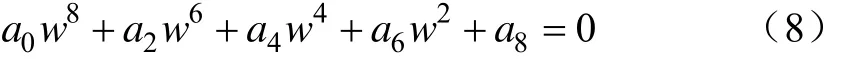
式中0a、2a、4a、6a、8a分别是与悬架系统参数相关的多项式系数。

在matlab平台上求解，可得精确解cw，将其代入到方程（7）可获得悬架系统失稳的临界时滞量cτ。

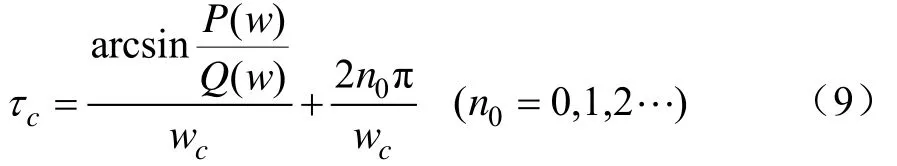
式中

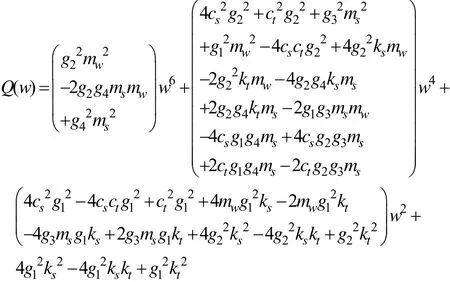
现用0l表示方程正实根的个数，当反馈增益1K取一定值时， l0的大小取决于方程系数 ai( i = 0 ,2,4,6,8)。当l0= 0，方程无正实根，系统不发生稳定性切换。当 l0≠ 0 ，方程正实根为{wc1, wc2,......,wcl}，每个 wcm(m = 1 ,...,l)对应着无限多个 τcn(n =1,2,… ∞)。当τc从τcn-ε增加到τcn+ ε （0 ＜ ε≪ 1 ,n =1,2,… ∞ ），方程特征根的变化趋势由下式确定：

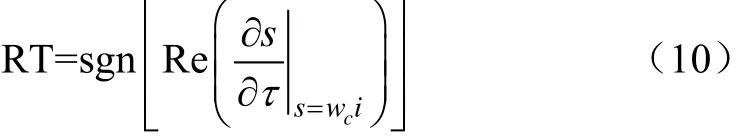
RT=+1表示τc从左至右穿过临界值τcn时，特征方程不稳定特征根的数量增加2个，RT=-1 表示τc从左至右穿过临界值τcn时，特征方程不稳定特征根的数量减少两个。基于以上的特征值分析，可以得到系统在一定反馈增益下时滞稳定和不稳定区间[27-28]。

利用2.1节中所取参数，在传统二次型最优控制律下，得到4个w值，分别为 wc1= 1 .784 7 r ad/s， wc2= 1 6.600 4 r a d/s，wc3= 3 1.3055rad/s， wc4= 9 7.697 3rad/s，每个w值对应于无数个临界时滞量，分别为 τc1= 0 .0558+3.520 6n1，τc2= 0 .014 3+0.3785n1， τc3=0.024 2+0.200 7n1，τc4=0.019 9+0.064 3n1（n1=1,2,…∞，单位为s）。依据特征值分析方法获得在反馈增益 K1下系统的时滞稳定区间为（0，0.014 3 s），时域响应仿真结果也说明了该稳定区间的正确性，为了进一步说明结果的正确性，下文从系统频域特性进行分析。

2.2 含时滞车辆悬架系统频响特性

根据频域响应求解过程，对悬架系统进行求解，通过对方程（1）进行傅里叶变换可得

式中

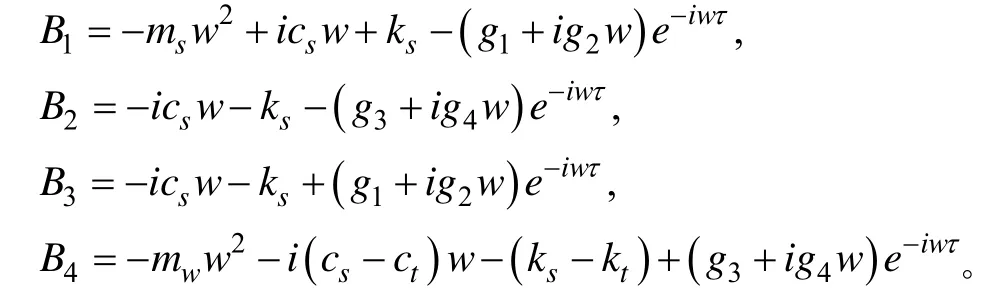
由式（11）可得路面激励对簧载质量位移的幅频特性为：

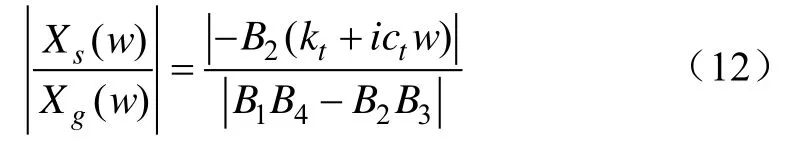
取1.2节中系统参数，根据式（12）仿真可得不同时滞量对系统幅频特性影响的曲线，如图3所示。

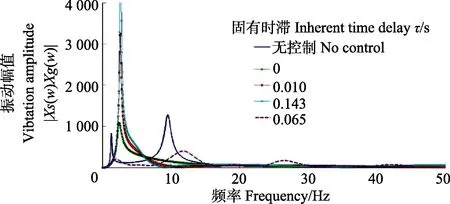
图3 时滞对系统幅频特性的影响Fig.3 Influence of time delay on amplitude frequency characteristics of system

从图3可以看出，与控制中无时滞（τ=0）相比，当控制时滞τ=0.01、0.0143s时，一阶主振型振幅随着时滞的增大而增大；当时滞 τ = 0 .065s时，系统的一阶振型振幅虽有所减少，但幅频特性曲线出现多个峰值，说明系统实际控制力与理想控制力不同步，系统出现“轮跳”现象，影响车辆行驶安全性。因此时滞对系统的控制效果影响极大，设计控制器时必须考虑时滞因素的影响。

3 车辆悬架系统时滞反馈控制

3.1 时滞反馈控制律设计

本文采用状态变换方法[29-31]对含时滞的半主动悬架进行变换，再利用最优控制理论设计系统时滞反馈最优控制律，以保证含时滞悬架系统的稳定性。针对含时滞的状态方程（2），进行如下积分变换，令

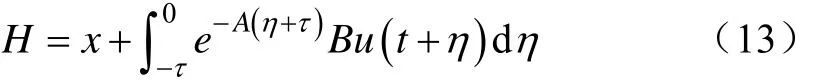
式（13）左右两边对时间t求导可得

将式（14）其代入方程（2）可得：

式中 B = e-AτB，从式（15）可以看出，变换后系统为不1显含时滞的状态方程，控制目标函数不变，利用二次型最优控制方法可获得其时滞最优控制律为：

式中= R-1(+ NT)，其中P~为下式Riccati方程的解。

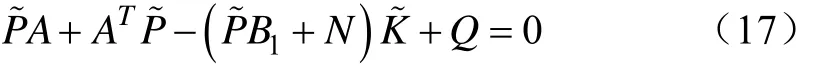
由式（13）和（16）可以看出，控制律中包含时滞τ和积分项，控制时积分项要通过计算获得。设采样周期为T，将时滞量表示为τ= l T - m ，其中l为大于0的正整数，m为小于T的非负 数 ， 采 用 零 阶 保 持 器 ， 即 当kT ≤t ＜ （ k + 1）T 时 ，u（ t） = u （ kT），所以当t = k T时，积分项可变换为

采用m= 0 进行分析，此时时滞量是采样周期的整数倍，式（19）可表示为：

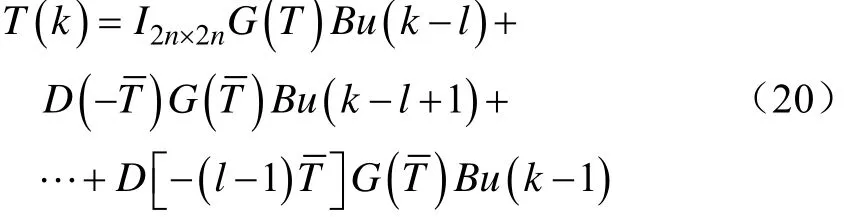
式中 G （ t）可通过下式进行迭代计算：

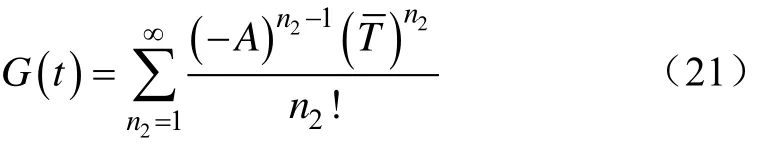
当t给定时， G （ t）将于有限步趋于常数矩阵[32]。

3.2 车辆悬架系统时滞反馈控制仿真

通过matlab/simulink平台，取1.2节中系统参数，在确定性激励 xg=0.004sin(2πft)、 f = 5 Hz下进行仿真计算，当系统时滞量为τ=0s时，时滞反馈控制退化为传统二次型控制，系统控制响应结果同图 2中固有时滞为0 s时结果；当 τ = 0 .010、0.0143、0.065s情况下，系统时滞反馈控制时域响应结果如图4所示。

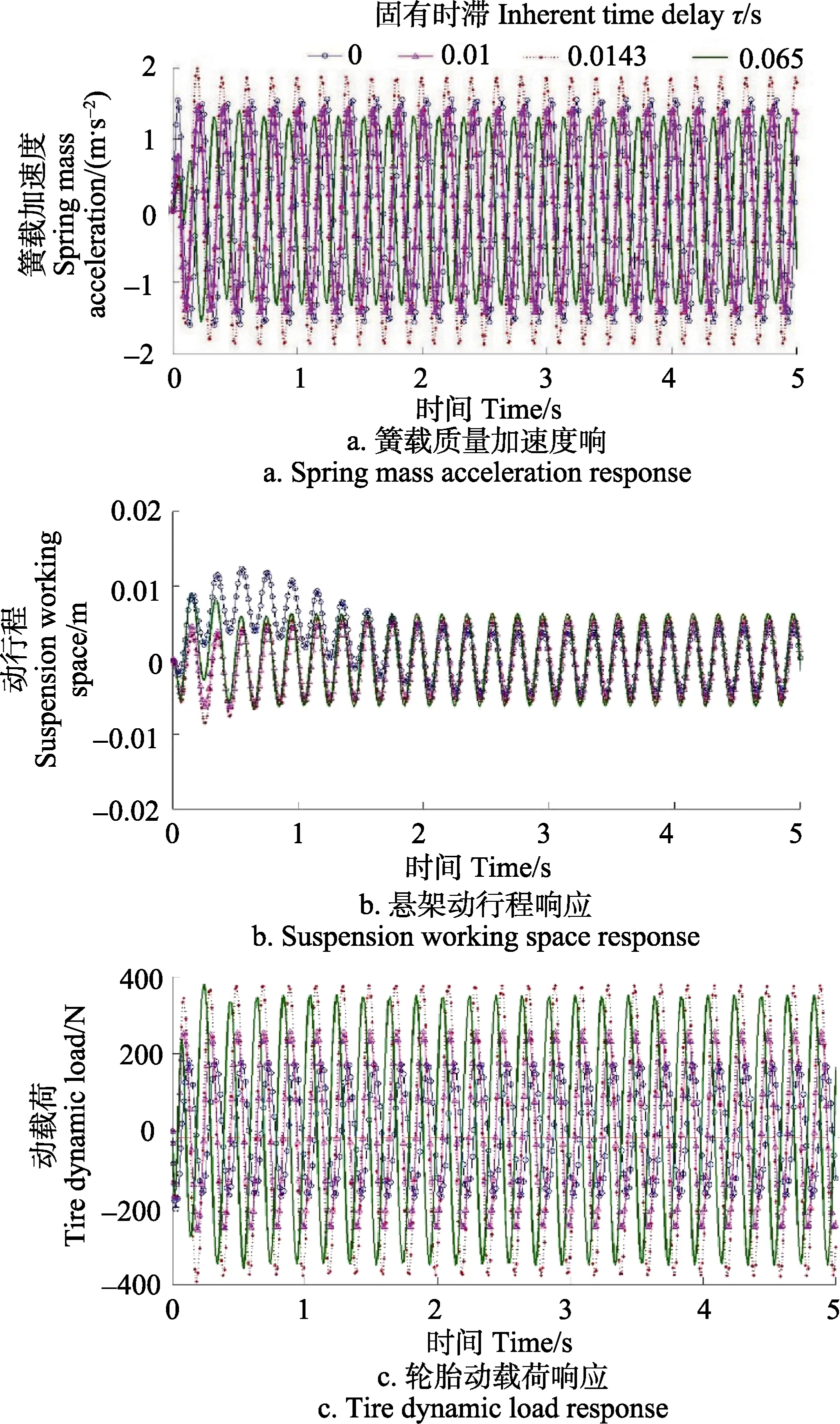
图4 时滞反馈控制系统时域响应Fig.4 Response of system with time delay feedback control

从图 4看出，在时滞反馈控制下，在 τ = 0 .010、0.0143、0.065s情况下，簧载质量加速度幅值稳定，分别为1.46、1.98、1.40 m/s2，因此，时滞大小不影响系统的稳定性，系统均保持稳定，克服了传统二次型最优控制无法保证时滞系统稳定性的问题，且与图 2中无控制情况下相比亦有减振效果，降幅最大为48.15%。

4 试验验证

4.1 试验系统参数

以 Lord公司磁流变阻尼器 RD-1005-3为控制作动器，采用加速度信号反馈搭建了悬架时滞试验平台，试验系统如图 5所示。振动控制器产生激励通过功率放大器、振动台作用于悬架模拟装置，采集卡采集 3个加速度传感器信号，传输至 PXI8196工控机，通过前文中控制算法程序计算获得控制力，并由输出卡、接线盒将其传输至磁流变阻尼器控制装置，进而实现系统减振。

悬架试验系统簧载质量及非簧载质量通过称量获得，刚度参数通过厂家定制，由厂家通过专业测量仪器测量获得，阻尼参数通过利用传递函数法对参数识别获得，主要参数如下：ms= 1 36.05kg，mw= 2 4.288kg，ks=10200 N/m，kt= 9 8000 N/m，ct= 1 5N·s/m，cs=153.11 N·s/m τ= 0 .065s，其中，时滞τ通过基于时域信号方法进行辨识，结合文献[4]中磁流变阻尼器响应时滞辨识结果最终确定。

图5 悬架时滞试验系统Fig.5 Suspension time delay test system

4.2 试验结果与分析

为了验证时滞反馈最优控制律设计的有效性，对含时滞 τ = 0 .065s悬架系统进行试验与仿真。试验时由振动控制器产生确定性激励 xg=0.004sin(2πft)、 f = 5 Hz作用于悬架模拟装置，通过采集、计算获得系统输出响应信号，并将其导入至Matlab平台中作图；仿真时采用与试验相同的工况和参数。试验和仿真所得系统输出响应时程曲线如图6所示。

对比图2和图6可以发现试验与仿真均有较好的减振效果，簧载质量加速度从无控制的2.70 m/s2约下降到1.50 m/s2，降幅为44.44%，且系统均保持稳定。试验所得簧载质量加速度幅值约为1.58 m/s2，比仿真结果1.40 m/s2略大，误差为12.56%，悬架动行程和动载荷误差分别为3.28%、12.39%，但误差在15%以内，一般工程计算误差可以取到 20%，甚至更高[33-35]，所以本文误差满足工程要求，说明试验结果与仿真结果具有较好的一致性。

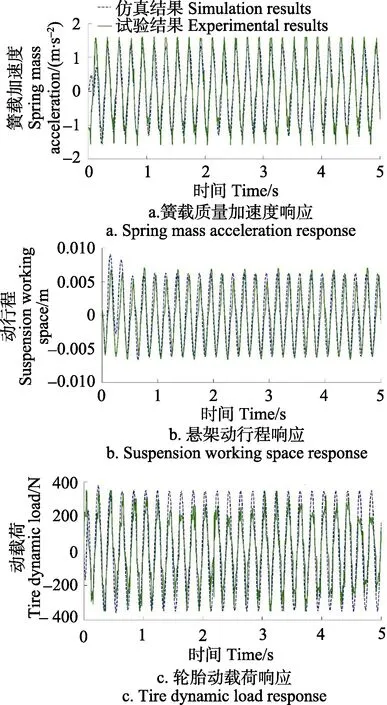
图6 时滞反馈控制下系统试验与仿真响应Fig.6 Experiment and simulation results of the system with time delay feedback control

5 结 论

本文以 2自由度含时滞悬架系统为研究对象，利用试验、理论和数值相结合的方法，研究了基于状态变换的悬架系统时滞反馈控制特性，获得以下主要结论：

1）建立了含时滞车辆2自由度悬架动力学模型，仿真和理论分析均表明采用传统二次型最优控制律对系统进行控制，可能会使系统定性特性发生改变，当系统固有时滞较大时，系统甚至会失稳发散，根据文中所取悬架和控制参数，在固有时滞为0.0143 s时系统就开始控制失稳发散。

2）通过积分变换思想和最优控制理论设计了车辆悬架时滞反馈最优控制律，仿真和试验结果均表明该控制律始终可以保证系统稳定，与无控制系统相比，簧载质量加速度从2.70 m/s2约下降到1.5 m/s2，降幅为44.44%，减振效果明显。

3）以磁流变阻尼器为作动器搭建了悬架时滞控制试验平台，采用基于时域信号辨识的方法获得了系统时滞约为 0.065 s，相同工况下试验与仿真结果具有较好的一致性，簧载质量加速度、悬架动行程、轮胎动载荷试验与仿真误差分别为12.56%、3.28%、12.39%，误差在15%以内，验证了研究结论的有效性与正确性，为悬架减振提供了有效的控制方法，具有重要的工程应用价值。

[1] 薛金林，汪珍珍，李毅念，等. 轮胎胎压和车速对无悬架拖拉机横向乘坐振动特性的影响[J]. 农业工程学报，2017，33(19)：94－101.Xue Jinlin, Wang Zhenzhen, Li Yinian, et al. Influence of tire pressure and forward speed on lateral ride vibration characteristics for unsuspended tractor[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(19): 94－101. (in Chinese with English abstract)

[2] 陆建辉，周孔亢，侯永涛，等. 基于遗传算法的厢式货车平顺性优化[J]. 机械工程学报，2017，53(20)：121－130.Lu Jianhui, Zhou Kongkang, Hou Yongtao, et al. Ride optimization of van truck based on genetic algorithm[J].Journal of Mechanical Engineering, 2017, 53(20): 121－130.(in Chinese with English abstract)

[3] 周长城，潘礼军，于曰伟，等.车辆钢板弹簧悬架系统减振器最佳阻尼匹配[J]. 农业工程学报，2016，32(07)：106－113.Zhou Changcheng, Pan Lijun, Yu Yuewei, et al. Optimal damping matching for shock absorber of vehicle leaf spring suspension system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016,32(7): 106－113. (in Chinese with English abstract)

[4] 聂佳梅，张孝良. 车辆被动天棚阻尼悬架系统台架试验[J].农业工程学报，2015，31(07)：66－71.Nie Jiamei, Zhang Xiaoliang. Experiment of vehicle passive skyhook damping suspension system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(07): 66－71. (in Chinese with English abstract)

[5] 易晨阳，张瑞亮，陈澔利，等. 重型商用车钢板弹簧悬架硬点优化设计[J]. 汽车技术，2017(03)：33－37.Yi Chenyang, Zhang Ruiliang, Chen Haoli, et al. Optimal design of leaf-spring suspension hard-points for a heavy commercial vehicle[J]. Automobile Technology, 2017(03):33－37. (in Chinese with English abstract)

[6] Crolla D，喻凡.车辆动力学及其控制[M]. 北京:人民交通出版社，2004.

[7] 汪若尘，陈龙，张孝良，等.车辆半主动空气悬架系统设计与试验[J]．农业机械学报，2012，43(4)：6－9.Wang Ruochen, Chen Long, Zhang Xiaoliang, et al．Design and test of semi-active air suspension system of vehicle[J].Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(4): 6－9. (in Chinese with English abstract)

[8] Spentzas K, Kanarachos S A. Design of a non-linear hybrid car suspension system using neural networks[J]．Mathematics and Computers in Simulation, 2002, 60(3－5): 369－378.

[9] Song X B, Ahmadian M, Southward S, et al. An adaptive semi-active control algorithm for magneto rheological suspension systems[J]．Journal of Vibration and Acoustics,2005, 127(5): 493－502．

[10] 张晗，过学迅，胡三宝，等. 液电式馈能半主动悬架控制特性仿真分析与能量回收验证[J]. 农业工程学报，2017，33(16)：64－71.Zhang Han, Guo Xuexun, Hu Sanbao, et al. Simulation analysis on hydraulic-electrical energy regenerative semiactive suspension control characteristic and energy recovery validation test[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017,33(16): 64－71. (in Chinese with English abstract)

[11] 陈杰平，冯武堂，郭万山，等. 整车磁流变减振器半主动悬架变论域模糊控制策略[J]. 农业机械学报，2011，42(5)：8－13．Chen Jieping, Feng Wutang, Guo Wanshan, et al. Whole vehicle magneto rheological fluid damper semi-active suspension variable universe fuzzy control simulation and test[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(5): 8－13. (in Chinese with English abstract)

[12] Yoshimura T, Kume A, Kurimoto M, et al. Construction of an active suspension system of a quarter car model using the concept of sliding mode control[J]. Journal of Sound and Vibration, 2001, 239( 2): 187－199．

[13] 孙会来，金纯，张文明，等. 考虑驱动电机激振的电动车油气悬架系统振动分析[J]. 农业工程学报，2014，30(12)：41－49.Sun Huilai, Jin Chun, Zhang Wenming, et al. Vibration analysis of hydro-pneumatic suspension system based on drive motor excitation force[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(12): 41－49. (in Chinese with English abstract)

[14] 赵彩虹，陈士安，王骏骋.刚度和阻尼系数对LQG控制主动悬架控制的影响分析[J]. 农业机械学报，2015，46(12)：301－308+354.Zhao Caihong, Chen Shian, Wang Juncheng. Influences of stiffness and damping parameters on control of active suspension based on LQG[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(12): 301－308+354. (in Chinese with English abstract)

[15] I Mihai, F Andronic. Behavior of a semi-active suspension system versus a passive suspension system on an uneven road surface[J]. Mechanics, 2014, 20(1): 64－69．

[16] 王刚，陈长征，于慎波. 含路面预瞄信息的车辆主动悬架有限频域多目标控制[J]. 农业机械学报，2015，46(12)：294－300.Wang Gang, Chen Changzheng, Yu Shenbo. Finite frequency multi-objective control of vehicle active suspension with road preview information[J].Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(12): 294－300. (in Chinese with English abstract)

[17] 宋刚，许长城. 考虑控制时滞的车辆主动悬架随机预瞄控制[J]. 农业机械学报，2013，44(6)：1－7.Song Gang, Xu Changcheng. Stochastic optimal preview control of active vehicle suspension with time-delay consideration[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(6): 1－7. (in Chinese with English abstract)

[18] 申永军，祁玉玲，杨绍普，等. 含时滞的单自由度半主动悬架系统的动力学分析[J]. 振动与冲击，2012，31(24)：38－40.Shen Yongjun, Qi Yuling, Yang Shaopu, et al. Dynamic analysis of a SDOF semi-active suspension system with time-delay[J]. Journal of Vibration and Shock, 2012, 31(24):38－40. (in Chinese with English abstract)

[19] 付文强，庞辉，刘凯. 含时滞天棚阻尼半主动悬架建模及稳定性分析[J]. 机械科学与技术，2017，36(2)：213－218.Fu Wenqiang, Pang Hui, Liu Kai. Modeling and stability analysis of semi-active suspension with sky-hook damper coefficients considering time delay[J]. Mechanical Science and Technology for Aerospace Engineering, 2017, 36(2): 213－218. (in Chinese with English abstract)

[20] 赵剡水，周孔亢，李仲兴，等. 磁流变减振器半主动悬架的系统时滞[J]. 机械工程学报，2009，45(7)：221－227.Zhao Yanshui, Zhou Kongkang, Li Zhongxing, et al. Time lag of magneto rheological damper semi-active suspensions[J].Journal of Mechanical Engineering, 2009, 45(7): 221－227.(in Chinese with English abstract)

[21] 廖英英，刘金喜，刘永强，等. 半主动控制与时滞对高速铁道车辆平稳性、稳定性及安全性的影响[J]. 振动与冲击，2011，30(06)：53－57.Liao Yingying, Liu Jinxi, Liu Yongqiang, et al. Effects of semi-active control and time delay on riding quality, running stability and safety of high-speed railway vehicle[J]. Journal of Vibration and Shock, 2011, 30(06): 53－57. (in Chinese with English abstract)

[22] Chen L X, Cai G P, Optimal control of a flexible beam with multiple time[J]. Journal of Vibration and Control, 2009,15(10): 1493－1512.

[23] Chen L X, Cai G P, Experimental study of delayed feedback control for a flexible plate[J]. Journal of Sound and Vibration,2009, 322(4－5): 629－651.

[24] Xu J, Chung K W, Zhao Y Y, Delayed saturation controller for vibration suppression in a stainless-steel beam[J].Nonlinear Dynamics, 2010, 62(1－2): 177－193.

[25] 申永军，田佳雨，赵永香. 含时滞半主动天棚悬架系统的解析研究[J]. 振动、测试与诊断，2014，34(6)：1110－1114．Shen Yongjun, Tian Jiayu, Zhao Yongxiang, et al. Analytical study on semi-active skyhook suspension with time delay[J].Journal of Vibration, Measurement & Diagnosis, 2014, 34(6):1110－1114. (in Chinese with English abstract)

[26] Ogata K．现代控制工程[M]. 北京: 电子工业出版社，2003.

[27] Wang Z H, Hu H Y, Delay-independent stability of retarded dynamic systems of multiple degrees of freedom[J]. Journal of Sound and Vibration, 1999, 226(1), 57－81.

[28] Wang Z H, Stability switches of dynamic systems with unknown parameters[J]. Journal of Sound and Vibration,2000, 233(2): 215－233.

[29] J N Yang, Z Li. Aseismic hybrid control of nonlinear and hysteretic structures II[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 1992, 118(7): 1441－1456.

[30] Kwon W H, Pearson A E. Feedback stabilization of linear systems with delayed control[J]. IEEE Trans-actions on Automatic Control, 1980, AC-25(2): 266－269.

[31] 蔡国平，黄金枝. 时滞线性系统振动主动控制的最优化方法[J]. 上海交通大学学报，2002，36(11)：1596－1599.Cai Guoping, Huang Jinzhi. Optimal control method for linear vibration systems with time delay in control[J], Journal of Shanghai Jiaotong University, 2002, 36(11): 1596－1599.(in Chinese with English abstract)

[32] 孙增圻. 计算机控制理论与应用[M]. 北京：清华大学出版社，1989.

[33] 张贵万，高发华，蒋兵，等. 麦弗逊悬架操稳性能优化与试验研究[J]. 汽车零部件，2016(11)：8－12.Zhang Guiwan, Gao Fahua, Jiang Bing, et al. Improvement and experiment on performance of vehicle handling stability for mac pherson suspension[J]. Automobile Parts, 2016 (11):8－12. (in Chinese with English abstract)

[34] 杨俊，王隽，王刚伟. 船舶推进轴系校中对轴系振动影响分析[J]. 动力学与控制学报，2016，15(2)：157－164.Yang Jun, Wang Jun, Wang Gangwei. Analysis on the effect of marine propulsion shafting alignment on its vibration [J].Journal of dynamics and control, 2016, 15(2): 157－164 (in Chinese with English abstract)

[35] 庞敬礼. 电磁主动悬架控制策略设计与试验研究[J]. 机械设计与制造，2017(11)：142－145, 148.

Pang Jingli. Control strategy design and experimental research on electromagnetic active suspension[J]. Machinery Design & Manufacture, 2017(11): 142-145+148. (in Chinese with English abstract)