基于Copula函数耦合性建模的二元加速退化数据统计分析方法
周 源,吕卫民,王少蕾,孙 媛
(1.海军航空大学, 山东 烟台 264001; 2.海军工程大学, 武汉 430000)
加速退化试验是一种高效评估产品可靠性的可行手段,已经普遍应用于产品研制、定寿、交付验收、延寿等多个阶段[1-3]。传统的加速退化试验只是测量产品某一个性能参数的退化数据,据此对产品可靠性进行建模与评估。然而一些产品存在多种退化失效过程,并且各退化失效过程之间可能存在耦合性,产品失效是各退化失效过程之间竞争的结果[4-6],因此,基于单性能参数加速退化数据的可靠性建模与评估方法已经不适用于多参数退化产品。
为了利用加速退化试验准确、高效地评估出多参数退化产品的可靠性,基于多元加速退化数据的统计分析方法逐渐受到关注[7-11]。文献[7]采用多元正态分布函数拟合多元性能退化数据,在假定均值与加速应力相关而协方差与加速应力无关的基础上建立了加速退化模型,然而,由于多元正态分布函数的适用性有限,此类方法的应用范围较小。文献[8]采用Gamma过程与Copula函数对多元加速退化数据统计分析,基于多元B-S分布建立了产品在额定应力下的可靠度函数。文献[9]利用基于退化量分布的方法对各性能退化过程建模,假定各相同测量时刻的退化量之间具有相关性并且亦采用Copula函数进行相关性建模。
继电器广泛用于国防工业的多种设备,主要功能是可靠地完成电信号传递、电路隔离、继电保护等,继电器的可靠性对整个设备能否正常工作非常重要[12-13]。对于很多用于军工、航天的继电器产品,会有一段比较长的贮存期,继电器在长期贮存过程中的某些性能指标不可避免会产生退化[13-15]。因此,如何对继电器的性能参数退化量进行合理统计分析,从而掌握继电器的质量变化规律是非常必要的。目前的性能退化数据统计分析方法大都是针对一种性能退化参数,然而工程经验表明继电器具有明显退化趋势的退化参数包括接触电阻值、释放电压。此外,由于继电器内部的结构相关性,接触电阻值、释放电压之间具有一定的耦合性,即任一种性能参数的退化过程会受到其他性能参数退化过程的影响。本文提出一种基于Copula函数耦合性建模的二元加速退化数据统计分析方法,结合加速退化试验评估某型继电器产品的可靠性。
1 二元加速退化数据建模
某型继电器存在两种性能退化过程,令Xp,k(t)表示产品在温度应力水平Tk下的第p个性能退化过程,其中p=1,2,任一性能退化过程首次达到失效阈值Dp时产品发生退化失效。根据前期的研究结论,Xp,k(t)服从Wiener随机过程,并且X1,k(t)与X2,k(t)之间具有耦合性。Tk代表第k个加速温度应力水平,ti代表第i次测量时间,xpjk(ti)表示Tk下第j个样品的第p个性能退化过程Xp,k(t)在时间ti的退化测量值,其中k=1,2,3;j=1,2,…,Nk;p=1,2;i=1,2,…,Mk。Tk下所有样品的性能退化测量值利用如下的数据结构描述:
(1)
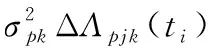
(2)
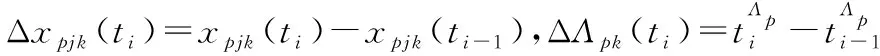
(3)
(4)
式(4)中,Φ(·)为标准正态分布的累积分布函数。根据文献[2]中的研究结论,Wiener过程的漂移参数值与扩散参数值都与环境应力水平相关,并且可利用加速模型定量表示它们的关系,如果环境应力为绝对温度Tk,可采用阿伦尼斯加速模型表示为
μpk=exp(ap-bp/Tk)
(5)
(6)
式(5)、式(6)中,ap,bp,cp为第p个性能参数对应的加速模型待估参数。
设G(x1),G(x2)分别为变量X1,X2的累积分布函数,根据Sklar’s理论,如果H(x1,x2)为G(x1),G(x2)的联合分布函数,则存在一个满足下式的Copula函数C(·),
H(x1,x2)=C(G(x1),G(x2);θ)
(7)
式(7)中,θ为Copula参数。目前应用较广的Copula函数为Gaussian,Frank,Gumbel,Clayton等,这4种Copula函数具有不同的耦合效果[16-18],表1给出了这4种Copula的分布函数及密度函数。
H(x1,x2)的概率密度函数为
c(G(x1),G(x2))g(x1)g(x2)
(8)
将式(4),式(5),式(6)代入式(7),得
H(Δx1jk(ti),Δx2jk(ti))=
C(Φ(U1jk(ti)),Φ(U2jk(ti));θk)
(9)

将式(3),式(9)代入式(7),得
h(Δx1jk(ti),Δx2jk(ti))=
c(Φ(U1jk(ti)),Φ(U2jk(ti));θk)g(Δx1jk(ti))g(Δx2jk(ti))

(10)
2 参数估计
参数估计的任务是提出有效的方法估计出二元加速退化模型的各待估参数值,包括以下10个参数:ap,bp,cp,Λp,e,f,其中p=1,2。根据式(10)建立如下极大似然方程:
g(Δx1jk(ti))g(Δx2jk(ti))}
(11)
然而由于待估参数过多,难以通过传统的极大似然估计法直接极大化式(11),无法一体化获取参数估计值。因此考虑采用Bayesian MCMC的思路[19],设计如下的参数估计算法一体化估计出各参数值,主要步骤为:
1) 令logLijk=log{c(Φ(U1jk(ti)),Φ(U2jk(ti));θk)g(Δx1jk(ti))g(Δx2jk(ti))};
2) 构建服从Poisson分布的伪随机变量Yijk,设Yijk的所有观测值为0并且Poisson分布的均值参数为-logLijk+R,如Yijk~Poi(0;-logLijk+R),R为一个满足-logLijk+R>0的实数;
3) 由Yijk的概率密度函数fP(0;-logLijk+R)建立如下极大似然方程,
(12)
4) 根据以下关系式将Poisson分布参数估计问题等效为二元加速退化模型参数估计问题
(13)
5) 在OPENBUGS软件中建立基于Poisson分布Yijk~Poi(0;-logLijk+R)的贝叶斯模型,将ap,bp,cp,Λp,e,f分别表示为服从无信息先验分布的随机参数,并设定各待估参数的初值;
6) 利用基于Gibbs抽样的马尔科夫链蒙特卡洛方法经过足够多步的迭代,获得ap,bp,cp,Λp,e的后验均值;
7) 判断各随机参数的后验分布是否收敛,如果收敛则将后验均值作为参数估计值,否则调整各随机参数的先验分布、待估参数初值、迭代步数,直到各随机参数的后验分布都达到收敛。
3 可靠性预计
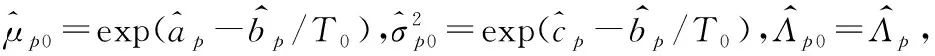
(14)
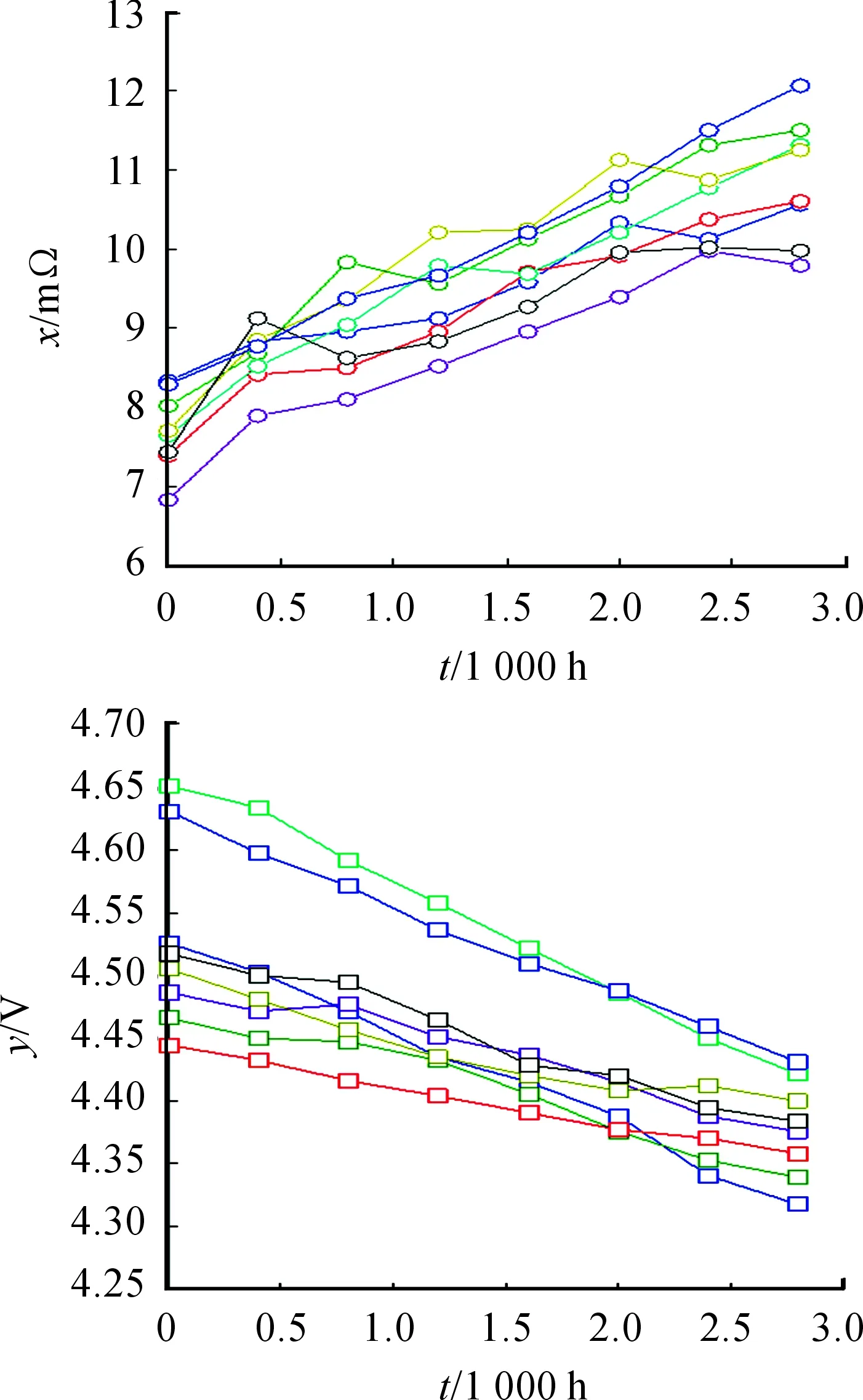
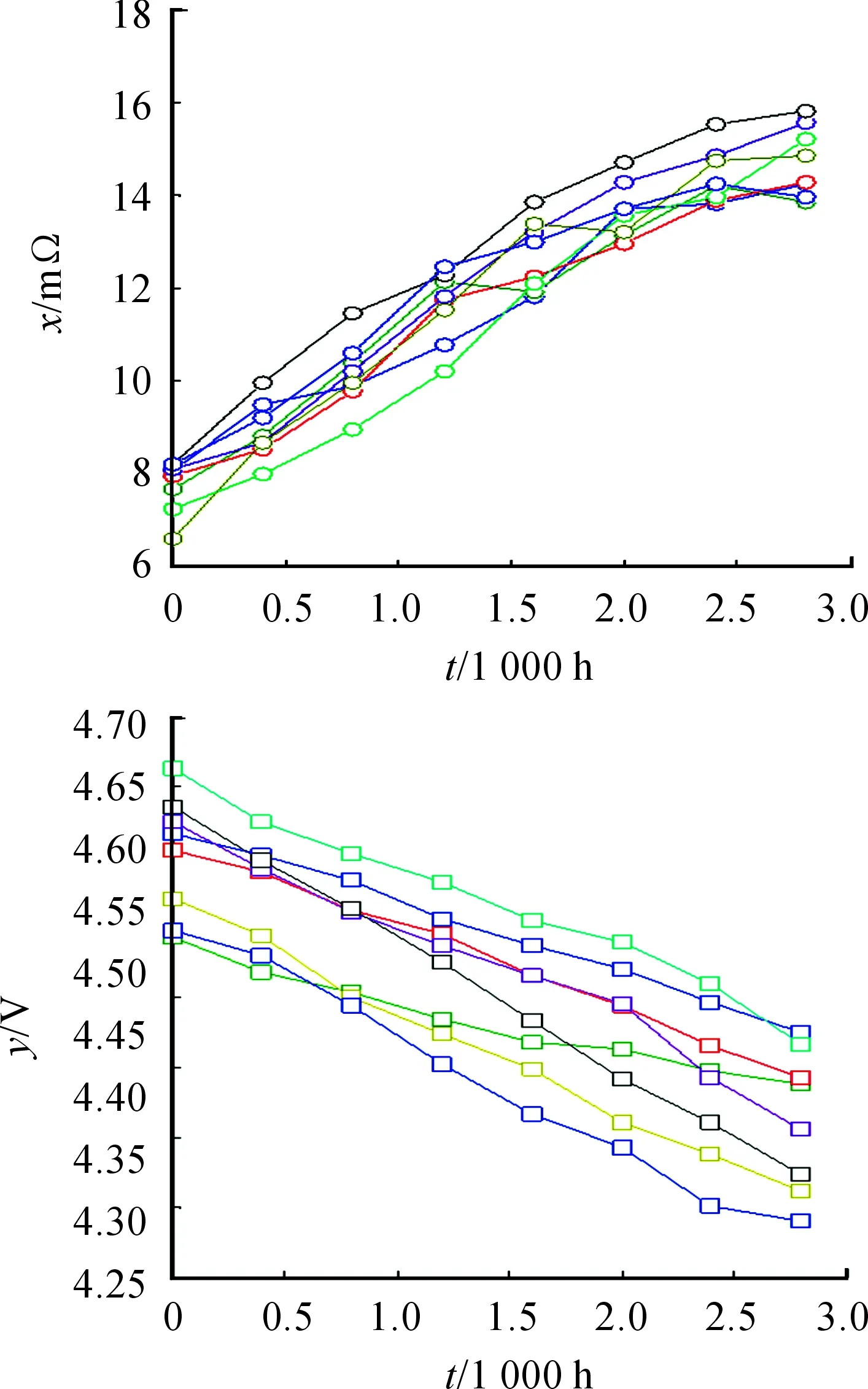
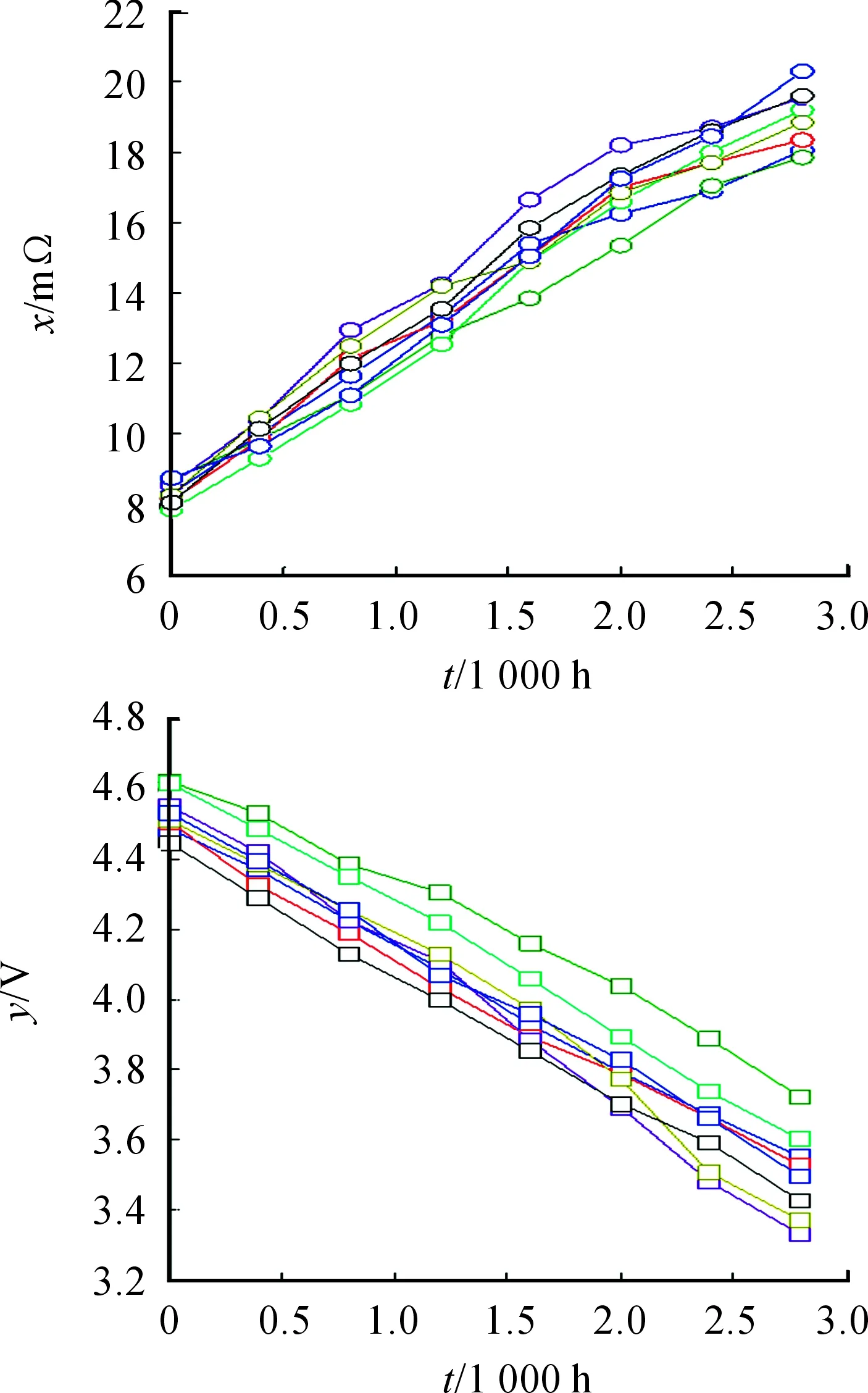
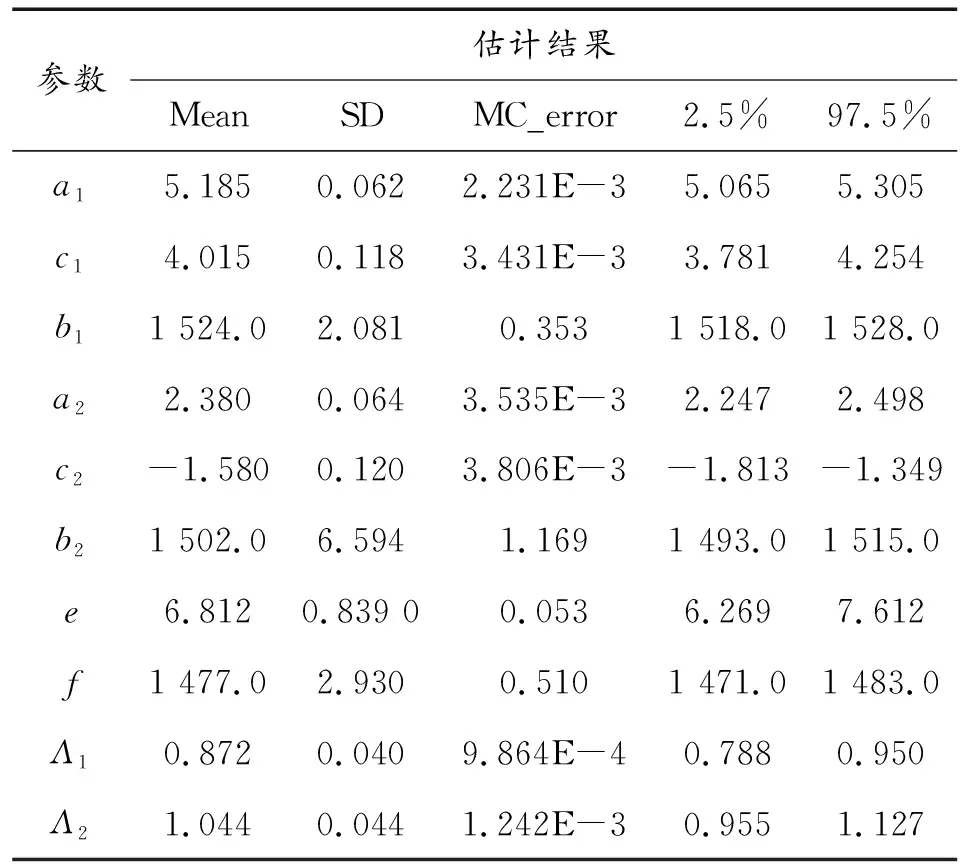
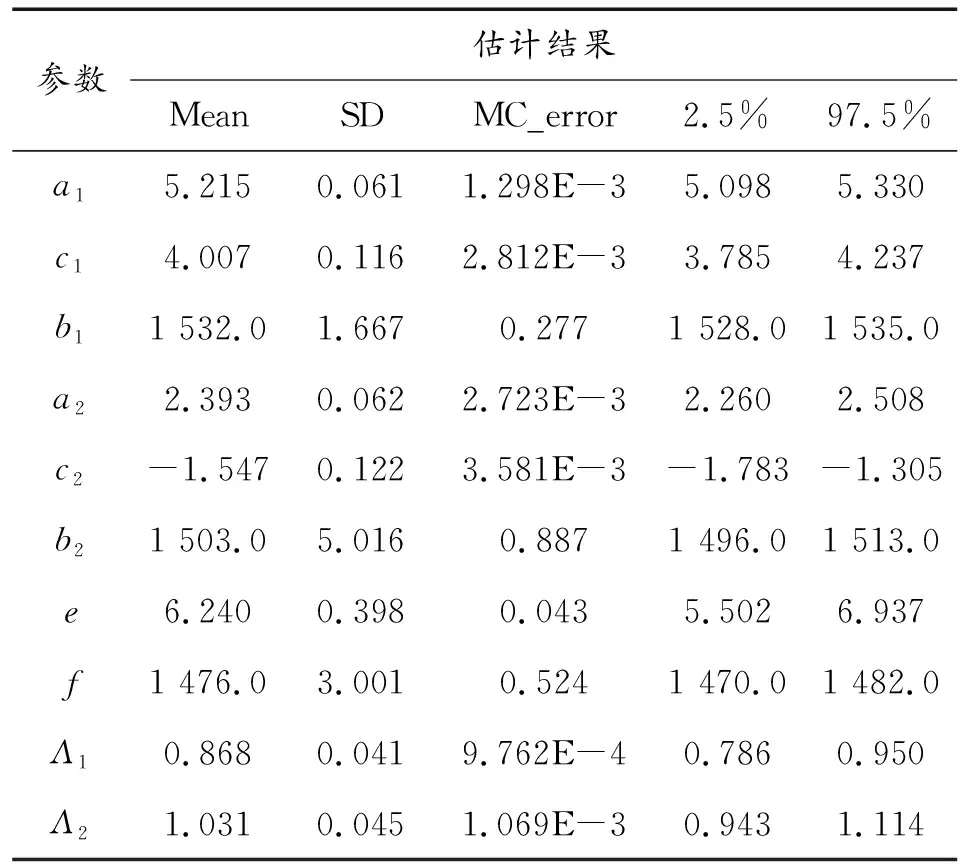
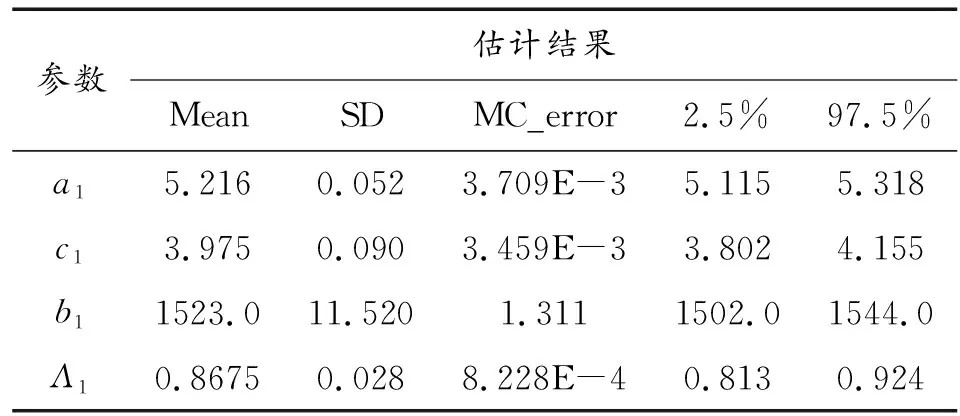
R0(t)=P(X1,0(t) (15) 式(15)中, (16) 如果X1,k(t)与X2,k(t)之间没有耦合性,则继电器的可靠度函数为 (17) 为了掌握某型继电器在长期贮存过程中的可靠性变化规律,首先结合以往的工程经验分析了此型继电器产品的失效模式与失效机理,得出:接触电阻增大、释放电压降低是产品在贮存过程中最主要的两种退化失效模式;接触电阻增大与释放电压降低两种失效过程存在某种程度的耦合性;温度是产品接触电阻增大、释放电压降低的敏感环境应力。然后,随机选取了24个样品开展了高温加速退化试验。具体试验信息为:在正常贮存温度25 ℃(298.16 K)下分别测量每个样品的接触电阻初值x0、释放电压初值y0;24个样品被平均分配到3个老化试验箱内,箱内的温度分别设为60 ℃(333.16 K),90 ℃(363.16 K),120 ℃(393.16 K);试验过程中每隔0.4×103h测量一次所有样品的接触电阻值x与释放电压值y,试验截止时间为2.8×103h。 图1、图2、图3展示了样品在3个温度应力水平下的接触电阻值与释放电压值的变化曲线。当接触电阻测量值相对于初值的变化量首次达到20 mΩ时或当释放电压测量值相对于初值的变化量首次达到2 V时,产品会发生退化失效。以下利用本文所提方法对二元加速退化数据进行统计分析,预测此型继电器产品在正常贮存温度下的贮存可靠度变化规律。 图1 继电器在333.16 K下的接触电阻及释放电压退化数据 图2 继电器在363.16 K下的接触电阻及释放电压退化数据 图3 继电器在393.16 K下的接触电阻及释放电压退化数据 首先,利用第1节中所提方法对此型继电器产品建立二元耦合加速退化模型,如式(9)所示,其中Copula函数类型分别选用Clayton Copula、Frank Copula。然后,利用第2节中所提方法进行参数估计。当选用Clayton Copula时,估计出各参数值如表2所示,当选用Frank Copula时,估计出各参数值如表3所示,其中Mean为随机参数的后验估计均值,SD为后验估计标准差,MC_error为MCMC参数估计的误差,2.5%表示后验估计值的2.5%分位数,97.5%表示后验估计值的97.5%分位数。比较表2与表3中的参数估计结果,各参数的后验均值虽然相差不大但均有一定变化,说明选用不同的Copula函数会影响最终的参数估计结果。通过比较AIC(Akaike Information Criterion)值,选用Clayton Copula的二元加速退化模型能够与试验数据拟合得更优。 表2 选用Clayton Copula时的参数估计 表3 选用Frank Copula时的参数估计 上式中, 表4 接触电阻加速退化模型的参数估计 表5 释放电压加速退化模型的参数估计 图4 可靠度评估结果 1) 针对某型继电器产品,提出了一种可行的二元加速退化数据建模方法,包括利用Wiener过程建立性能参数的退化模型;结合阿伦尼斯方程建立模型参数的加速退化模型;采用Copula函数建立二元加速退化过程之间的耦合性模型。 2) 提出了一种基于Bayesian MCMC的参数估计,有效解决了因为二元加速退化模型中待估参数过多,传统估计方法不适用的难题。 3) Copula函数能够描述两种退化过程之间的耦合性,但也给可靠性建模与参数估计增加了难度。 4) 通过所提方法评估了某型继电器的可靠性,与工程实际中的认识相符,但评估结果还需产品的真实贮存失效数据做进一步验证。 [1] LI J X,WANG Z H,LIU X,et al.A Wiener process model for accelerated degradation analysis considering measurement errors[J].Microelectronics Reliability,2016,65(10):8-15. [2] 滕飞,王浩伟,陈瑜,等.加速度计加速退化数据统计分析方法[J].中国惯性技术学报,2017,25(2):275-280. [3] WANG H W,XU T X,MI Q L.Lifetime prediction based on Gamma processes from accelerated degradation data[J].Chinese Journal of Aeronautics,2015,28(1):172-179. [4] 王浩伟,奚文骏,冯玉光.基于退化失效与突发失效竞争的导弹剩余寿命预测[J].航空学报,2016,37(4):1240-1248. [5] 王浩伟,滕克难,李军亮.随机环境应力冲击下基于多参数相关退化的导弹部件寿命预测[J].航空学报,2016,37(11):3404-3412. [6] WANG Y P,PHAM H.Modeling the dependent competing risks with multiple degradation processes and random shock using time-varying Copulas[J].IEEE Transactions on Reliability,2012,61(1):13-22. [7] 潘骏,王小云,陈文华,等.基于多元性能参数的加速退化试验方案优化设计研究[J].机械工程学报,2012,48(2):30-35. [8] PAN Z Q,BALAKRISHNAN N.Reliability modeling of degradation of products with multiple performance characteristics based on gamma process[J].Reliability Engineering and System Safety,2011,96(8):949-957. [9] 王孟.基于Copula函数的多元加速退化试验方法研究[D].杭州:浙江理工大学,2013. [10] TSAI T R,SUNG W Y,LIO Y L,et al.Optimal two-variable accelerated degradation test plan for Gamma degradation processes[J].IEEE Transactions on Reliability,2016,65(1):459-468. [11] ZHANG X P,SHANG J Z,CHEN X,et al.Statistical inference of accelerated life testing with dependent competing failures based on Copula theory[J].IEEE Transactions on Reliability,2014,63(3):764-780. [12] 李文华,马思宁,沈培根,等.振动条件下铁路继电器寿命预测研究[J].电气工程学报,2017,12(7):8-15. [13] 叶雪荣,林义刚,黄晓毅,等.航天继电器贮存过程吸合时间退化机理研究[J].电工技术学报,2017,32(11):173-179. [14] 孟彦辰.基于性能参数退化的航天继电器可靠性建模与评估研究[D].哈尔滨:哈尔滨工业大学,2015. [15] 王浩伟,滕克难.基于加速退化数据的可靠性评估技术综述[J].系统工程与电子技术,2017,39(12):2877-2885. [16] FAN M F,ZENG Z G,ZIO E,et al.Modeling dependent competing failure processes with degradation-shock dependence[J].Reliability Engineering and System Safety,2017,165(7):422-430. [17] 潘正强.加速应力下二元退化可靠性建模及其试验设计方法[D].长沙:国防科学技术大学,2011. [18] PENG W W,LI Y F,YANG Y J,et al.Bivariate analysis of incomplete degradation observations based on inverse Gaussian processes and Copulas[J].IEEE Transactions on Reliability,2016,65(2):624-639. [19] NTZOUFRAS I.Bayesian Modeling Using WinBUGS[M].Hoboken,New Jersey,John Wiley & Sons,2009. [20] PAN Z Q,BALAKRISHNAN N,SUN Q.Bivariate constant-stress accelerated degradation model and inference[J].Communications in Statistics-Simulation and Computation,2011,40(2):247-257.4 案例应用

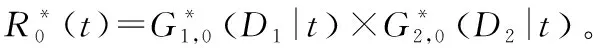

5 结论

