无起爆药雷管燃烧转爆轰的二维两相流数学模型

李梦娇，王雨时，闻 泉

(南京理工大学 机械工程学院, 南京 210094)

炸药燃烧和爆轰是由化学反应和流体运动相耦合形成，在一定的条件下燃烧可以转变为爆轰。但是，它们有着本质的区别：燃烧主要通过扩散燃烧气体与热传导辐射的传播这两种途径达到的，而爆轰是沿炸药传播的爆轰波对未爆轰炸药的冲击压缩引起化学反应实现的。但燃烧和爆轰又是相互联系的，当炸药燃烧的稳定性受到破坏以后，就有可能形成爆轰。这是由于炸药的燃烧产物进入未燃炸药孔隙中和炸药的孔壁，灼热的气体燃烧产物点燃未反应多孔炸药，点燃速度大于逐层燃烧速度。稳定燃烧被破坏的充分必要条件是气体相对于孔隙壁的平均流入速度必须大于装药逐层燃烧的线速度。

火药燃烧过程是一个伴随强烈化学反应，具有多维效应的高温、高压、瞬态燃烧过程，加上影响火药燃烧的因素很多，难以比较全面地了解火药燃烧各项参数，给人们研究火药燃烧状况带来了许多困难。这种高温、高压的情况下，只通过实验来获取信息显然已经不够，必须借助于数值模型以便获取更多的信息研究火药安全性、压力波动、燃烧不稳定性等问题。

如今火工品的安全性越来越受到重视，人们开始对安全性较高的雷管加以研究，在1973年，美国研制出了两种无起爆药燃烧转爆轰雷管，它们所用主装药均为太安。俄罗斯和日本也相继研制出了高安全性雷管。我国在20世纪80年代中期，正式研制出第一款无起爆药雷管，至今已研制出多种可靠性高、安全性好的无起爆药雷管。

本研究针对某无起爆药雷管内火药的燃烧转爆轰问题，建立二维两相流模型，给出了控制方程及定解条件，并基于数值方法求解，对进一步研究雷管内火药的燃烧和爆轰过程有关参数有重要意义。

1 物理模型

图1为某无起爆药燃烧转爆轰雷管结构模型，其中点火药装药为硼硝酸钾，中间药装药为六硝基芪。电点火具点火后，就会点燃其附近的点火药，其周身温度也会快速提升，四周火药的表面温度也会在对流热交换的影响下有所提升，当温度提升至一定高度时便会点燃火药，在火焰峰的推动下，所有的火药将会陆续燃烧起来，药室内压强不断上升，继而发生燃烧转爆轰反应,最后向底火药输出能量。

1.电热桥丝点火点; 2.点火药装药区; 3.中间药装药区; 4.底火药装药区; 5.能量输出端

图1 物理模型结构示意图

根据该雷管结构，可以确定数值计算模型的边界，有：

点火药装药区L0=5.5 mmR=2 mm

中间药装药区L0=10.5 mmR=2 mm

两个装药区均为规则的圆柱空间，因此二维计算区域均为规则的矩形。

计算过程中做以下假设:

a)药室内流动为轴对称二维两相流动；

b)高温瞬态表面加热情况下，加热层很薄，固体内部温度基本不变，故不考虑固相能量方程；

c)不考虑雷管壁的热散失和形变；

d)火药燃烧反应过程中的颗粒力学性能(颗粒屈服强度和颗粒剪切模量)视为不变。

2 数学模型

2.1 守恒方程

基于以上假设，根据气固两相流体力学理论，可以得到以下基本方程：

1) 气相质量守恒方程

2) 气相动量守恒方程

r方向(径向)

z方向(轴向)

3) 气相能量守恒方程

4) 固相质量守恒方程

5) 固相动量守恒方程

r方向

z方向

2.2 辅助方程

1) 气体状态方程

当压力超过600 MPa之后，如当考虑燃烧向爆轰的转变时，压力可能在0.1 ms时间内迅速上升到20 GPa甚至更高。这时应采用余容修正的状态方程:

其中

z1=A+Bρ+Cρ2+Dρ3+…

式中：α为余容；cv为等容比热；γ比热比；z1为压缩因子；z是气体密度ρ的函数；ρ的范围为0.1～5.0g/cm3，即气体从稀疏状态变化到类固体状态都是适用的；A，B，C，D……分别为第一、二、三、四……级维里系数。

2) 粒间应力

式中：α=1/ε；G为剪切模量；α0为初始值；Y为材料屈服强度，塑性变形首先在外表处出现，逐渐向颗粒中心传递，式中分段特征量为

3) 相间热交换

根据火药的点火燃烧过程，目前多数人依据流化床条件下的结果，即采用Gelperin和Einstein的关系式：

式中：Pr为普朗特数；Rep为雷诺数。于是热交换系数：

hc=kgNup/dp

气体导热系数用kg表示，单位为W/(m·k)，也代表温度函数，其中：

kg=[131.034+0.262 68(T-400)]×10-3

因此，相间单位面积上的热流量：

q=hc(T-Tps)

式中Tps为颗粒表面温度。

一般条件下，对普朗特数可取常量

式中γ为比热比。

该表达式并不是唯一的，采用与真实火药形状和尺寸相同的试样，用质/热比拟法得到火药燃烧条件下的结果：

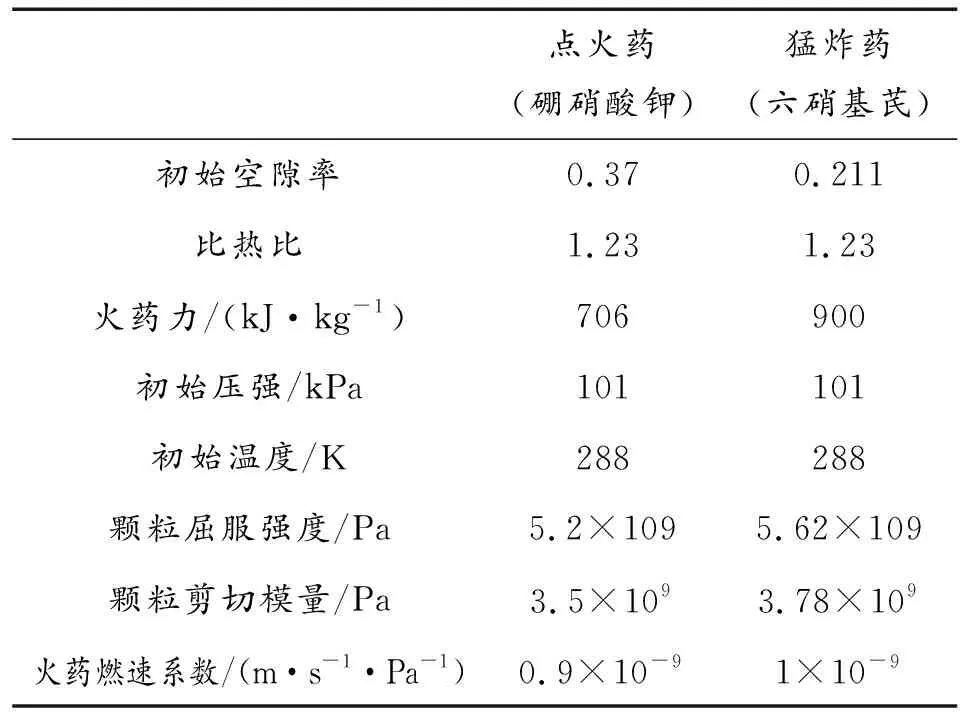
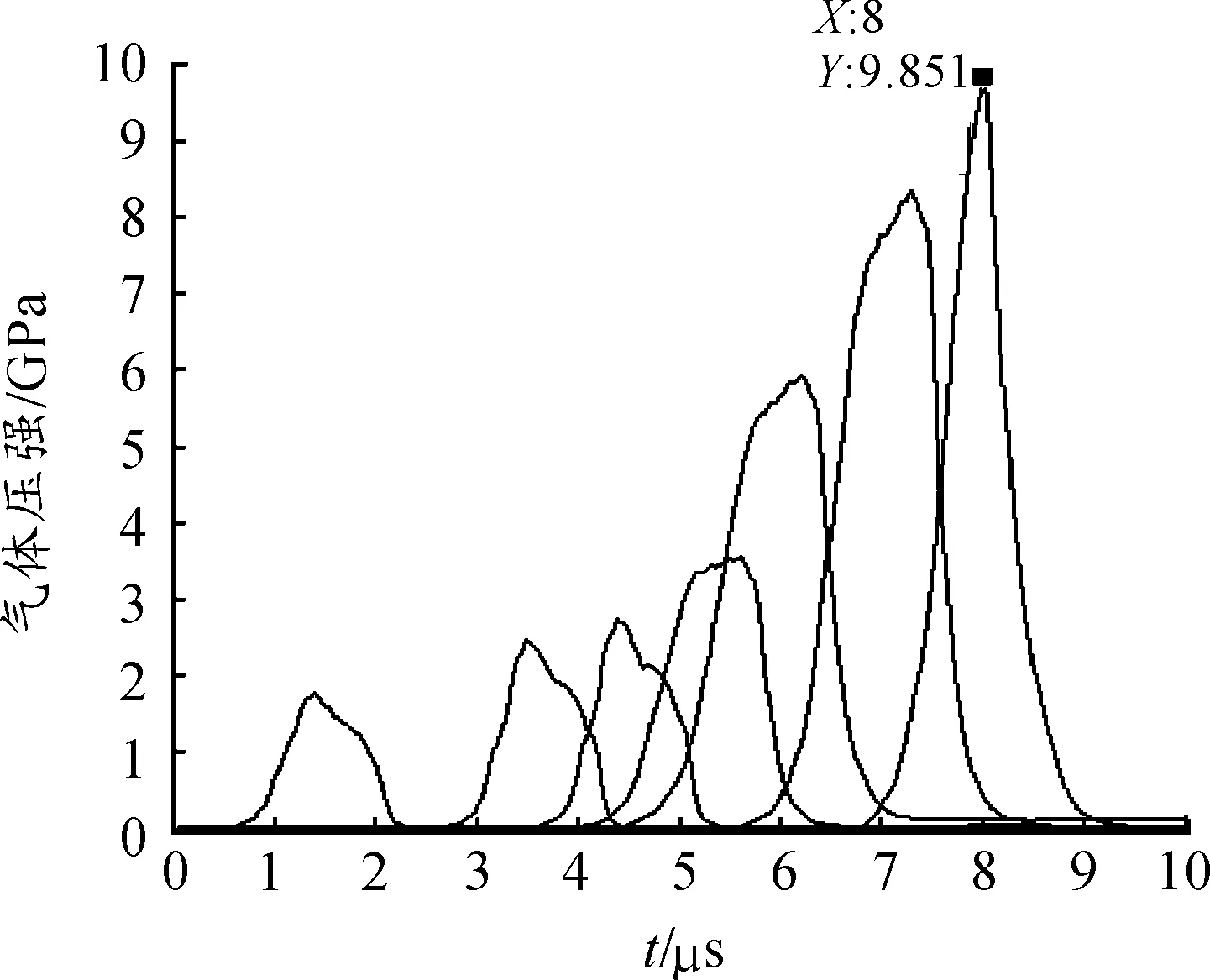
该式适用范围为3 500

此外，膛内的辐射传热是不可忽略的因素。因为气相与颗粒表面之间的温差一般为2 000 K,按斯蒂芬一玻尔兹曼定律估算，即

式中εp为颗粒表面黑度，近似取εp=0.95～1.0。斯蒂芬-玻尔兹曼常量σ=5.656 94×10-8J/(s·m2·K4)。模仿对流换热，则辐射换热可表示为：

qr=hr(T-Tps)

则综合变换可得

估算表明，当Rep=1 850～2 216时，hr≈hc。所以在火药燃烧传热问题中，可以认为

h=hr+hc

即气相与固相表面之间的传热系数是对流系数与辐射系数之和。特别对于火药燃烧转为爆轰后，辐射传热更是不可忽略的因素。

4) 人工黏性项

在流体力学计算过程中，无论初值条件及边值条件给定得如何光滑，都可能产生间断解。因而如何计算解的间断，是流体力学计算中的一个不可忽视的问题。在二维两相流计算中，点火过程的猛烈程度及装药床的透气性决定了在整个燃烧转爆轰过程中，燃烧场空问压强梯度的大小。当压强梯度非常陡峭时，常常使计算难以进行。所以在二维两相流数值计算中，除了格式本身应具有一定的耗散性之外，一般还要加入一定的人工黏性项，采用的是Pycatob型耗散方法。即对于方程

在两个空间偏导数项中均加入附加项，可变换为

这里υ和u分别为X和Y方向的气相速度，且有

式中，c为当地音速。实践证明，这种黏性项不仅使用方便，而且非常有效，易于程序实现，还能很好地保持流场中各量的原有特征。

除上述提到的基本方程和辅助方程外，还有药形函数、体积燃烧量、当量直径等参数的计算方法，不再一一赘述，可参照文献[1]。

3 燃烧转爆轰数值模拟结果及分析

采用MacCormack差分格式求解偏微分方程组的数值结果。

在某雷管药床内进行燃烧转爆轰数值模拟，计算参数如表1所示，取等间距检测单元，计算得到中轴线上各检测单元气体压强-时间曲线如图2所示。

表1 点火药和中间药数值计算参数

图2 中轴线上各检测单元气体压强-时间曲线

根据燃烧转爆轰机理分析，装药区内的点火药在t=0.22 μs时已经被点燃，发生燃烧反应，开始燃烧产生气体产物，在点火位置的最高压强只有1.774 GPa，这是由于点火药刚被点燃，炸药分解，气体产物较少；随后，靠近点火端的点火药继续发生燃烧反应，燃烧产物增加，压强增大，开始形成压缩波，因为燃烧波具有压缩作用，在其影响下，炸药内部的点火药应力分布出现不均匀现象，导致在未反应的炸药部分过于应力集中，使得其内部的空隙与空穴温度过高，这种现象实际上就是常说的“热点”。若空隙或空穴处的温度处于持续升高，火药便会分解，热点范围也随之扩大，不仅限于空隙或空穴，而是连成一片，燃烧的速度明显加快；之后燃烧波在火药压缩波的推动下使猛炸药燃烧起来，使得气体产物产生速度明显加快，压强也随之增加。炸药燃烧速度随着压强与温度的提升而加快，使对流燃烧的速度提升，所得产物的速度明显提升。炸药的燃烧速度在压缩波的推动下也快速提升。在猛炸药中，高温高压气体和固体形成冲击波向前传播，燃烧产物继续向周围膨胀，最终在t=8 μs时在能量输出端最大压强达到9.851 GPa， 大于六硝基芪的爆轰压强，形成爆轰。

4 结论

数值模拟的结果表明：选取的硼系点火药和猛炸药经过反应燃烧后可以完成燃烧转爆轰，输出能量可以引爆二级火工品。这对于无起爆药雷管燃烧转爆轰的研究与试验具有实际意义。

[1] 王升晨.膛内多相燃烧理论及应用[M].北京：兵器工业出版社,1994.

[2] 金志明，宋明.火药压缩模量及颗粒间应力[J].兵工学报，1990(1)：27-35.

[3] 周彦煌,张明安，王升晨.火炮装药床中气固相间换热系数实验的研究[J].兵工学报，1992(2)：19-23.

[4] 张建忠,侯聪花,胡双启.含能材料装药安全性在力学性能及数值模拟方面的研究进展[J].兵器装备工程学报,2010,31(5):11-13.

[5] YEHIA S,EL-TEMSAHERIK J.Effects of nano-sized zero-valent iron (nZVI) on DDT degradation in soil and its toxicity to collembola and ostracods[J].Chemosphere:Environmental toxicology and risk assessment,2013(1):44-50.

[6] LEONARD E SCHWER．Impact and detonation of Comp-B an example using the LS-DYNA EOS：Ignition and growth of reaction in high explosiVes[C]//12th international LS-DYNA users conference．[S.l.]:[s.n.],2013：1-20．

[7] 李海庆，张小兵，李筱炜，等.激光多点点火二维两相流数值模拟[J].兵工学报，2012(33)：257-260.

[8] 晁李金,吕秉峰.点火药量对发射药燃烧性能的影响[J].兵器装备工程学报，2016(3):126-128.

[9] 张永丽，杨慧群.新型含能材料的研究进展[J].兵器装备工程学报，2012(2):123-125.

[10] BERNECKER R R,PRICE D．Burning to Detonation Transition in Porous Beds of a Highenergy Propellant[J]．Combustion and Flame，2012，48:219-231.

[11] 苏俊，刘玉存，王建华．无起爆药雷管内管装药密度对燃烧转爆轰的影响研究[J]．中国安全科学学报，2012，22(1)：82-87.