无线电调频引信谐波提取改进算法
刘非凡,刘忙龙,曹少珺
(机电动态控制重点实验室, 西安 710065)
在无线电调频引信的定距算法中,谐波提取是整个算法不可或缺的一部分[1],谐波提取的处理精度和实时性直接影响定距算法最终的定距性能,因此对谐波提取算法的设计显得至关重要[2-3]。
目前的研究中,ARM芯片已成功替代传统模拟电路结构,在引信的信号处理、信号采集领域得到了应用[4]。由于ARM芯片自身属于冯诺依曼结构,只能对数据进行串行处理,因此处理时间相对较长[5]。文献[6]通过短时傅里叶变换对信号时域进行分段谐波提取,又利用重叠采样的方法减小的采样间隔,保证了谐波提取的处理精度。由于采样样本的重叠,大大增加了需要处理的数据总量,因此降低了谐波提取算法的实时性。为了解决实时性不足的问题,文献[7]采取了简便算法,即只对信号的频率进行大致的估算,以此来推导引信与目标的相对距离。该方法有效提升了实时性,但算法的简化却降低了处理精度。若能在保证处理精度的前提下提升实时性,会使谐波提取算法的处理能力明显提升。本文针对ARM芯片在无线电引信高处理精度的定距算法中处理速度不足的问题,提出了谐波快速提取改进算法。
1 谐波提取算法及重叠采样方法
1.1 基于短时傅里叶变换的谐波提取算法
根据无线电调频引信的原理,炮弹与目标的相对距离与发射信号和回波信号的差频频率有关[8]。但由于差频信号不规则区的存在,导致差频频率无法直接反应距离的变化。要想得到炮弹与目标的相对距离,需对差频信号进行时频域转换,在频域得到其各次谐波的幅值,并通过对谐波的幅值进行连续的观察,最终得到弹目相对距离随时间的变化关系[9]。为得到谐波幅值随时间的连续变化关系,通常采用短时傅里叶变换对差频信号进行处理。即利用相同的窗函数在时域上连续对采样信号进行截取,将采样信号分为若干个采样段,再对各采样段分别进行傅里叶变换得到其各自的频域波形。
但短时傅里叶变换的采样方法自身存在缺陷,每个短时变换的窗函数过窄,窗内的信号采样点数量不够,会导致频率分析不够精准,频率分辨率差。窗函数过宽,时域上又不够精细,时间分辨率低[10]。
1.2 重叠采样方法
如前文所述,传统采样方法中各次傅里叶变换之间时间间隔较大,由此造成了信号处理的精度较低,现有的改进方法中,保持采样点数为 1 024点不变,每组傅里叶变换的起始点之间间隔32个采样点,而非之前间隔 1 024点进行采样(如图1所示)。此种采样方法中的采样点会在不同的傅里叶变换中重复利用,各采样段的窗函数会在时域上发生重叠,增加运算量。但因为减小了起始点与起始点之间的采样间隔,提高了短时傅里叶变换的等效采样频率。等效采样频率由之前的1 kHz提升到了32 kHz,随着等效采样频率的提高,处理精度也得到了提升。
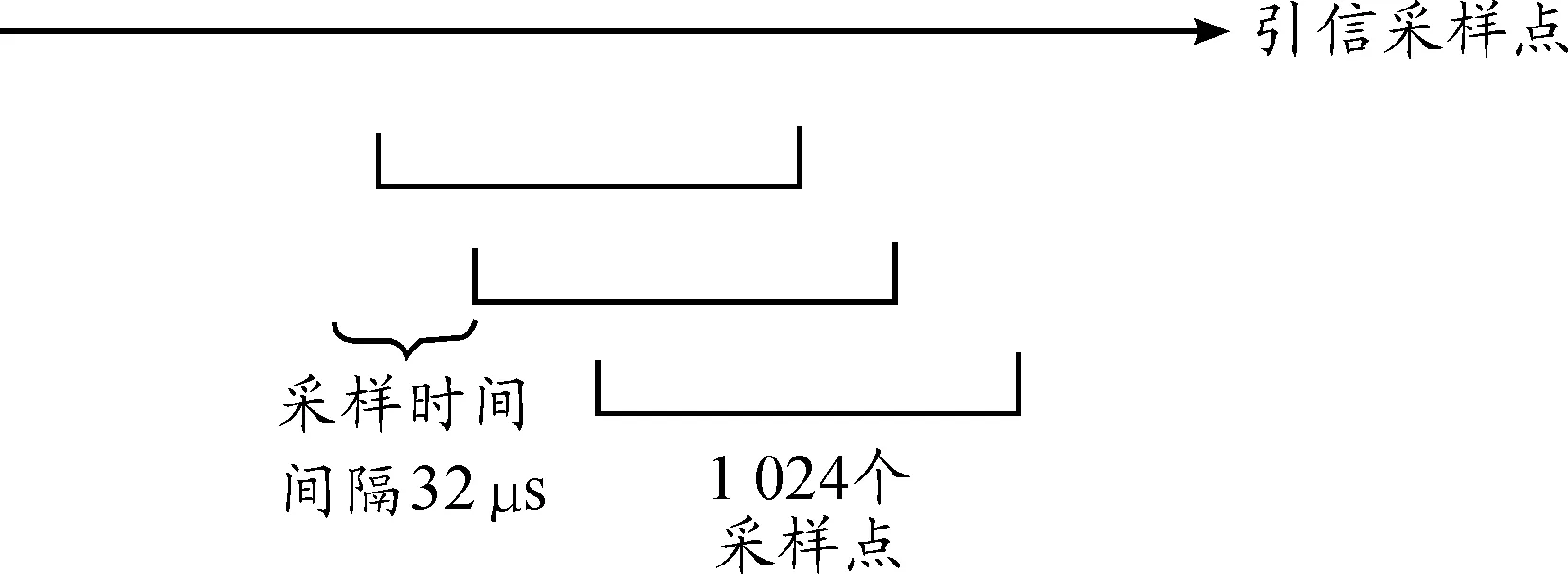
图1 重叠采样方法示意图
1.3 重叠采样对实时性的影响
通常情况下,处理短时傅里叶变换各段数据最有效的手段是对其分别进行快速傅里叶变换(FFT)。但快速傅里叶变换耗费系统资源较多,加之重叠采样方法数据量过大,若按重叠采样方法进行采样,虽然处理精度得到了满足,但处理实时性严重降低。以本文选用的STM32F407芯片为例,该芯片以ARM cortex M4作为内核,并自带DSP模块。STM32F407芯片可以使用自身DSP库中的快速傅里叶变换函数进行1 024点的快速傅里叶变换。该函数由芯片生产厂家提供,内部程序已经过反复优化。因此可以认为该函数处理时间为STM32F407芯片快速傅里叶变换所能达到的最快速度。该函数进行一次快速傅里叶变换平均需耗时0.58 ms。若按前文所述的重叠采样的方法进行采样,一秒钟的采样时间内共获得了31 969个采样段,每个采样段都包含 1 024个采样点。对每个采样段分别进行快速傅里叶变换提取谐波,共需处理时间18 542.02 s。此处理时间远大于采样时间一秒钟,完全不能满足信号实时处理的需要。因此,需要对快速傅里叶变换算法进行进一步的改进。
2 无线电调频引信谐波快速提取改进算法
前文提到的重叠采样算法已可以满足谐波提取算法的精度要求,为了在不降低处理精度的前提下提高实时性,需要从理论层面对算法运用的公式进行等效代换,削减不必要的计算量。本文利用离散傅里叶变换(DFT)和复数运算的性质对原有算法进行改进。
离散傅里叶变换的公式为:
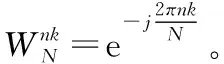
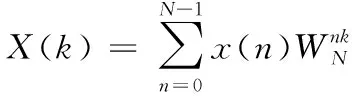
(1)
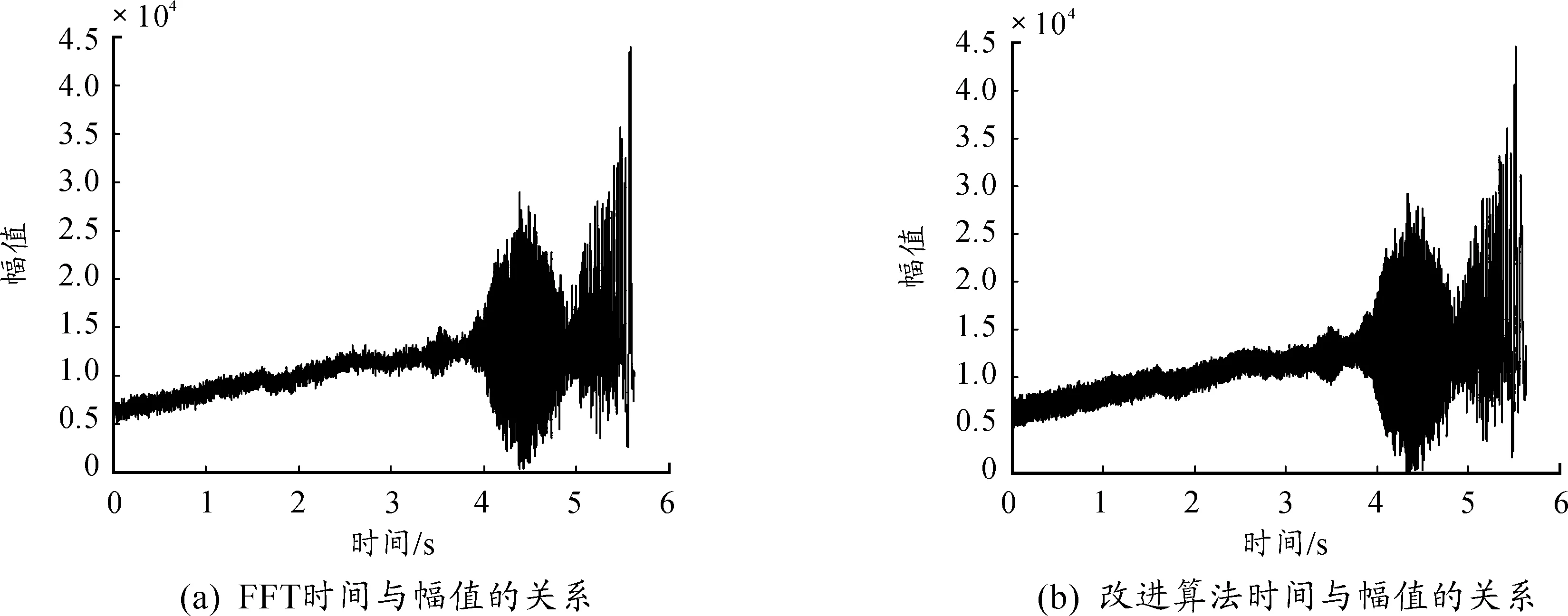
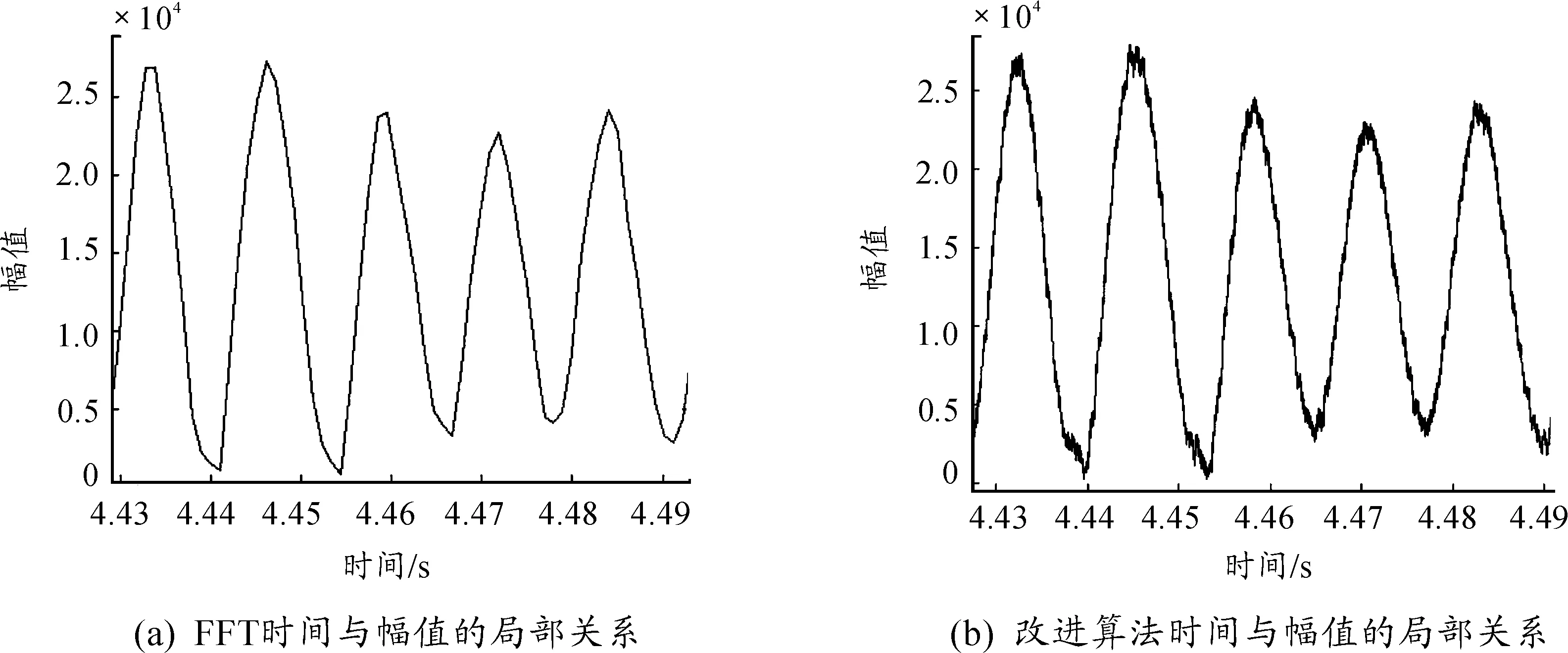
根据前文所述的采样方案,需后移M个点(M (2) 现保留式(1)中第M项到第N项的复数乘法运算结果,用x(N+1)—x(N+M)替换掉式(1)中x(1)—x(M-1),得到如下等式: (3) 对式(3)进行进一步整理,得: (4) 因为最终求得的是对应点的幅值,因此要对X(k)进行取模运算。对向量相加后的和向量求模时,运算结果只与相加前各向量的长度以及向量之间的相对夹角度数有关,而与向量自身的角度无关。式(2)与式(4)中各项复数的模值均相等,各项间的夹角亦为定值且相等,因此对式(2)与式(4)整体取模后|X2(k)|=|X3(k)|。 而式(4)中,x(M+1)—x(N)对应项的值均与式(1)中的对应项相等,需要进行复数乘法计算的只有x(N+1)—x(N+M)的对应项,即只需进行M次复数乘法就可完成新一轮DFT运算。因此应用式(4)计算方法代替式(2)后,可大大减小程序整体的运算量,提高运算速度。 综上,该算法利用离散傅里叶变换和复数运算的性质,对重叠采样中重复元素的计算结果进行反复利用,即不再对未处理采样段中重复元素进行二次计算,而是直接使用已处理采样段中重复元素的计算,避免了重复计算,以此提升谐波提取算法的运算速度。 第一节介绍的基于重叠采样的短时傅里叶变换已可以满足谐波提取的精度要求。利用Matlab软件进行仿真,分别运行改进前的谐波提取算法和改进后的算法,若改进后的算法对谐波的提取结果与改进前一致,则可以说明改进后的算法能够满足谐波提取算法处理精度的要求。 本仿真实验选取采样频率为1 MHz的无线电调频引信推板实验数据,数据共5 632 000个采样点。两种算法均采用短时傅里叶变换进行信号四次谐波的提取,改进前的算法采用快速傅里叶变换对各采样段进行处理,改进后的算法利用第二节所述的方法对各采样段进行处理,每个采样段均为1 024个点。实验结果如图2、图3所示。 从图2及图3可以看出,两种算法计算出的差频信号四次谐波的宏观走势完全一致,改进算法的细节分辨率也不低于改进前的算法,两组实验对信号的处理结果相同,说明改进算法确实不会降低谐波提取的处理精度。 使用C语言编写改进算法,利用以ARM为内核的STM32F407芯片运行该程序。统计程序运行时间,并与Matlab的处理结果进行比较。STM32F407芯片利用DSP库中自带的基4快速傅里叶变换函数arm_cfft_radix4_f32(),对上述数据进行一次1 024点的快速傅里叶变换共需耗时 0.58 ms,而改进算法的单次傅里叶变换仅耗时0.019 ms,完成全部176 000次傅里叶变换共耗时3.283 s。按前文所述,数字信号处理芯片在一秒中的时间内最少需要完成 31 969次运算才能满足实时性的最低需求,而改进算法平均一秒钟可完成53 610次运算,完全符合实时性的要求。 将STM32F407芯片的处理结果导入Matlab,生成与时间的关系图,处理结果如图4所示。将图4与图2及图3对比可以看出,在使用相同算法的情况下,STM32芯片的处理结果与Matlab的处理结果完全一致,数据实际处理结果与理论仿真结果相符。改进算法在保证了处理精度前提下有效提升了信号处理的实时性。 图2 FFT与改进算法的时间与幅值关系 图3 FFT与改进算法的时间与幅值局部关系 图4 STM32处理结果 本文提出的无线电调频引信谐波快速提取改进算法,是指利用离散傅里叶变换和复数的运算性质,对重叠采样中重复元素的计算结果进行反复利用,即不在未处理的采样段中对重复元素进行二次计算,而是直接使用已处理采样段中重复元素的计算结果,在不改变信号最终处理结果的前提下削减了计算量,减少了短时傅里叶变换即谐波提取算法的运算量。通过仿真及实验验证表明:进行一次1 024点的快速傅里叶变换处理耗时0.58 ms,而改进算法的单次傅里叶变换仅耗时0.019 ms。改进算法的实际性能与理论分析结果一致,与以前的算法相比运算效率得到了提升,可在不降低信号处理精度的前提下缩短信号处理所需的时间,解决了在处理精度过高时,以ARM为信号处理芯片的引信谐波提取算法实时性不足的问题。 [1] 彭业凌.线性调频引信信号的分选和识别[D].北京:北京理工大学,2015. [2] 卢新栋,李艳萍.调频引信信号处理器模块化改进[J].制导与引信,2014,35(2):14-17. [3] 张伟.基于ARM的雷达信号处理系统的研究[D].南京:南京理工大学,2008. [4] 张晨.基于ARM微处理器的引信数据采集系统设计[D].南京:南京理工大学,2014. [5] STM32F40x和STM32F41x产品手册[Z].意法半导体,2012. [6] 高磊.宽带雷达中频回波长脉冲压缩采样重构中的分段重叠处理及其机理分析[J].信号处理,2011,27(7):967-974. [7] 巩艳华.基于STM32的连续波线性调频引信系统设计与实现[J].科技信息,2014(9):71. [8] 崔占忠,宋世和.近炸引信原理[M].北京:北京理工大学出版社,2009. [9] 赵慧昌.无线电引信设计原理与方法[M].北京:国防工业出版社,2012. [10] 卢广阔.基于短时分数阶傅里叶变换的谱分割算法[J].电波科学学报,2017,32(4):474-481.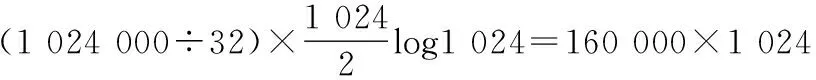
3 实验验证
3.1 Matlab仿真验证
3.2 引信芯片实测
4 结论

