二自由度冗余驱动并联机器人的动力学研究

宋 婷，宋 拓，张小力

(1.陕西铁路工程职业技术学院， 陕西 渭南 714000; 2.西安理工大学， 西安 710048)

二自由度冗余驱动并联机器人区别于传统机器人，它有许多连杆和关节，并且结构复杂、封闭，系非线性动力学系统，它的复杂在于具有很多个输入、输出，耦合关系十分复杂，在系统中存在冗余驱动，这使得并联机器人的动力学分析和建模非常复杂。并联机器人的动力学分析建模是一项非常重要的课题，动力学模型的准确性直接影响着并联机器人的动态性能、结构优化和结构设计及动力学仿真等研究工作。要使并联机器人在运动学方面达到速度高和精度高，就要有一套适用于动力学效果显著的控制算法。所以，要研究机器人控制，首先要进行动力学分析研究。

1 拉格朗日法(Lagrange)

拉格朗日方程是最常用的并联机器人建模方法，采用此方法建立的动力学模型能够描述各构件之间的耦合关系。其通式如下：

(1)

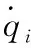
选取并联机器人3个主动关节角度变量为广义坐标，构造Lagrange动力学模型：

(2)

(3)

(4)

将式(2)、式(3)、式(4)代入式(1)，可得

(5)

合并后得

(6)

有如下性质[7]：

1)M(q)是对称正定矩阵，即：

MT=M

uTMu>0, ∀u∈Rn,u=0

2 拉格朗日—达朗伯法

达朗伯原理将复杂的动力学问题转化为静力学问题求解。在分析力学领域，把这种变换了形式的求解方法与虚功原理相结合，产生了拉格朗日——达朗伯方程，该类方程已成为分析和求解动力学问题行之有效的方程之一[8]。通常将机器人的并联结构化简为开链结构再进行动力学分析。从该闭链结构中选择任意一个非驱动关节，采用虚拟切割法将其切割成开链结构，该开链结构满足拉格朗日—达朗伯方程：

(7)

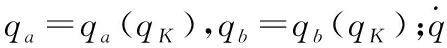
当并联机构在奇异位形外且正常驱动，则：

(8)

其中：W是q相对于qa的雅可比矩阵；I为单位矩阵。树形开链结构的动力学方程为：

(9)

若树形开链结构Lagrange函数L等于闭链结构Lagrange函数Lv，则L=Lv，由此便得到闭链关节驱动力矩τa和树形开链关节驱动力矩τ的关系，即WTτ=STτa。因而该并联机构的动力学方程为：

(10)

3 应用拉格朗日—达朗伯方程建立二自由度冗余驱动并联机器人动力学模型

以固高GPM系列二自由度冗余驱动并联机器人实验平台为对象，采用拉格朗日—达朗伯方程建立该系统的动力学数学模型，对其进行动力学分析，其结构简图如图1，各关节位置参数如表1。

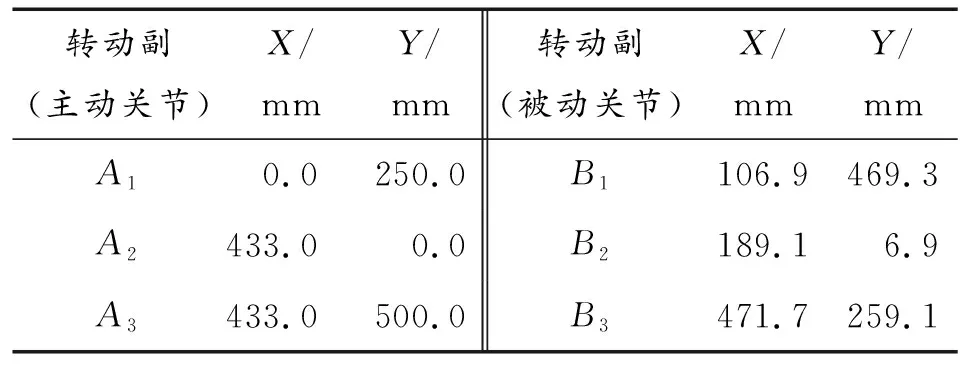
转动副(主动关节)X/mmY/mm 转动副(被动关节)X/mmY/mm A10.0250.0B1106.9469.3A2433.00.0B2189.16.9A3433.0500.0 B3471.7259.1

以固定转动副的转轴方向为Z轴，Z轴与机器人运动平面垂直，以水平向右的射线为x轴、竖直向上的射线为y轴，建立坐标系，x轴和y轴的交点即为坐标原点。由于此机器人不仅结构对称而且具有三组同样的运动分支，所以研究其动力学方程只需要取其中一个分支进行分析即可，如图2所示，建立参考坐标系oxy，坐标系的原点位于该并联机器人结构简图中正三角形A1A2A3的中心。

令该机器人第i((i=1,2,3))个分支中两均质细直杆的长度分别是l1和l2，其质量分别是mi1和mi2，质心坐标为(xi1,yi1)和(xi2,yi2)，质心即为杆件的中心点，两杆的质心距离杆端部的距离分别为r1和r2，与x轴正方向的夹角分别为αi和βi，由图2可知两杆质心沿x轴和沿y轴的方程：

(11)

(12)

对式(11)、式(12)求导，可获得速度方程：

(13)

(14)

1) 该分支在水平面上的运动动能为：

(15)

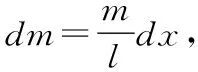
(16)

同理：均质细直杆l2绕质心B(xi2,yi2)旋转得到的转动惯量为：

(17)

由动能定理可知：

则：E即为连杆做旋转运动的动能。

l1和l2绕质心旋转的动能为：

(18)

由上可知，该分支的总动能为：

(19)

若设该机器人运动平面为基准面，不考虑关节间的摩擦，则系统势能为零，用Pi表示，则Pi=0。拉格朗日算子L=E-P，可知：Li=Ei-Pi=Ei。

根据式(1)，可得出用关节坐标αi和βi来表述该分支的动力学方程：

(21)

(22)

由式(21)、式(22)可得：

(23)

(24)

K3=m2l1r2

将式(23)与式(24)结合后，可表示成如下形式：

(25)

式中：

合并这3个运动分支的动力学方程，可获得闭链系统的动力学通式：

(26)

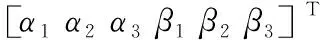
文献[11]可知该机器人的速度方程，即：

(27)

式中：di=l1[(x-xi0)sinαi-(y-yi0)cosαi]

ei=x-xi0-l1cosαi

fi=y-yi0-l1sinαi

同理：

(28)

式中：λi=li[-(x-xi0)sinβi+(y-yi0)cosβi]

μi=x-x01-l2cosβi

γi=y-y01-l2sinβi

该机器人速度方程式(27)与式(28)结合，可写成如下形式：

(29)

(30)

即：

其中：S和Q是一个η1=η2=η3=0的矩阵

则：将式(29)和式(30)合并后，可得该机器人的速度雅可比矩阵，用J表示，J是一个6×2的矩阵：

由于用质心坐标表示二自由度冗余驱动并联机器人系统中相互独立的广义坐标矢量，且由式(10)可得其动力学方程：

(31)

式中：

u=[xy]T

由式(31)可知，采用拉格朗日—达朗伯方程建立的动力学数学模型，可以直接求得逆动力学方程，采用此方法建立的动力学模型和采用达朗伯法或拉格朗日法等方法所建立的动力学模型相比，具有一致性[12]，说明拉格朗日—达朗伯法在求解机器人动力学方程和建立模型中具有明显的优越性及可行性。

4 二自由度冗余驱动并联机器人驱动力优化

由于该机器人存在冗余驱动，驱动关节力和力矩的分配具有不确定性，在式(31)中，若已知驱动力τa，即机构的运动可以确定；若已知机构的运动，而不能唯一确定τa，此时则要借助优化方法对驱动力τa进行优化分配。通过对τa进行优化可以减小机器人各关节内力，防止驱动力突变，进而使并联机器人的力传递性能得到提高，并且还可改善并联机器人的动态性能。

将驱动力优化问题描述如下：

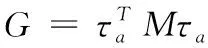
引进Lagrange因子，根据代数方法可得Lagrange函数：

(32)

(33)

(34)

由式(27)和式(28)求得：

(35)

f=Hτa

(36)

将式(29)代入式(30)，得：

(37)

由式(31)可知：

λ=2(H(M-1)THT)-1f

(38)

将式(32)代入式(29)，得：

τa=(M-1)THT(H(M-1)HT)-1f

(39)

若取M为单位矩阵，可求得τa为：

τa=HT(HHT)-1f=JT(JJT)-1f

(40)

式(40)是当机器人末端执行器所受负载已知时，求并联机器人驱动力的最优解。

平面二自由度冗余驱动并联机器人理论上只需两个电机即可满足该机器人的自由度数，才能够确定并联机器人末端执行器的运动情况，而此机器人却给出了三个驱动电机，使驱动构件数目大于机构末端执行器自由度数目，则已知末端执行器输出力时，无法唯一确定机器人的驱动力。分配驱动力理论上会有许多组解，依据机构运动不同的工作状况，选择不同的优化目标及方法对驱动力τa进行优化分配。该并联机器人的优化目标有两种：能耗优化和输入力优化。依据二自由度冗余驱动并联机器人的实际工作情况，本节采用优化输入力的方法[16]对驱动力进行优化分配。

机器人末端执行器所受两个作用力分别为：

1) 并联机器人各分支的轴向驱动力，表示为τa=[τa1,τa2,τa3]；

2) 作用在末端执行器处外负载矢量f，表示为：

f=[fx,fy,fz]

当末端执行器力位于平衡状态时，其所受到合力为零，平衡状态方程为：

(41)

优化目标函数为：

τa=minτai

(42)

将式(41)和式(42)相结合便可获得优化驱动力τa。

5 结论

文章基于二自由度冗余驱动并联机器人的简化模型，针对该机器人系统动力学分析建模的复杂性，采取拉格朗日—达朗伯法对该机器人进行动力学分析建模，通过该方法建立动力学数学模型，不仅可以直接求得逆动力学方程，而且与单独采用拉格朗日法所建立的动力学模型相比具有一致性，说明：

1) 拉格朗日—达朗伯法在机器人动力学模型的求解中具有明显的优越性及可行性；

2) 采用输入力优化法对该机器人驱动力进行优化分配，对改善并联机器人动力学性能提供了充足的理论依据。

[1] 惠记庄，魏芳胜，高凯，等.基于ADAMS的冗余驱动并联机器人动力学仿真研究[J].工程设计学报，2012，19(5):362-365.

[2] 解本铭，赵词海.基于ADAMS的3-P4R并联打磨机器人运动学仿真[J].制造业自动化，2011,33(8):21-25.

[3] 赵景波.MATLAB控制系统仿真与设计[M].北京：机械工业出版社，2010.

[4] 贠远，徐青松，李扬民.并联微操作机器人技术及其应用进展[J].机械工程学报，2008,12:12-23.

[5] TRUNG DO THANH,JENS KOTLARSKI,BODO HEIMANN,et al.Dynamics identification of kinematically redundant parallel robots using the direct search method[J].Mechanism and Machine Theory，2012(52):277-295.

[6] 冯宝奇.LINKS-EXE700R并联机床在制造领域的应用[J].航空制造技术，2009,4:96-97.

[7] 张立杰，刘辛军.平面二自由度驱动冗余并联机器人的机构设计[J].机械工程学报,2002，38(12):49-53.

[8] 侯锦世.分析力学中的达朗伯原理[J].山东轻工业学院学报,1995，9(4)：65-66.

[9] SU Y X,ZHENG C H.Global asymptotic tracking of robot manipulators with a simple decentralized non-linear PD-like controller.[J].Control Theory&Applications,2010,4(9):1605-1611.

[10] SERDAR KUCUK.Energy minimization for 3-RRR fully planar parallel manipulator using particle swarm optimization[J].Mechanism and Machine Theory.2013(62):129-149.

[11] SUN D,MILLS J K.Adaptive synchronized control for coordination of multirobot assembly tasks[J].IEEE Trans.Robot.Autom.,2002,18(4):498-510.

[12] YOUNG B,HO KIM.SHINICHI HIRAI.Modular and Distributed Forward Dynamic Simulation of Constrained Mechanical Systems——A Comparative Study [C].New Orleans,LA,April 2004.

[13] 高天国.并联机床加工中心的研制与应用[J].航空制造技术，2009,5:50-53.

[14] TRUNG DO THANH,JENS KOTLARSKI,BODO HEIMANN,et al.Dynamics identification of kinematically redundant parallel robots using the direct search method[J].Mechanism and Machine Theory.2012(52):277-295.

[15] 赵景山，冯之敬，褚福磊.机器人机构自由度分析理论[M].北京：科学出版社，2009.

[16] 魏立新.6-DOF 并联机器人动力学建模及其控制策略研究[D].秦皇岛：燕山大学，2002：72-86.

[17] 李增刚.ADAMS入门详解与实例[M].北京:国防工业出版社，2009:79-81.

[18] WANG Xuanyin,YIN Ruiduo.Six-axis force/torque sensor based on stewart platform[J].Chinese Journal of Mechanical Engineering,2008,44(12):118-122.

[19] 刘延斌，张宏敏，赵新华.3-RRRT并联机器人鲁棒自适应模糊滑模控制[J].电机与控制学报，2009，(13)：87-91.

[20] 刘金琨.机器人控制系统的设计与MATLAB仿真[M].北京：清华大学出版社，2008.

[21] 贾振元，李映军，张军，等.并联式轴用压电六维力/力矩传感器[J].机械工程学报，2010(6):62-63.

[22] 赵景山，冯之敬，褚福磊.机器人机构自由度分析理论[M].北京：科学出版社，2009.

[23] 王凯正，林棻，张华达，等． 基于Arduino的轮式移动机器人速度控制模式比较[J].重庆理工大学学报(自然科学)，2017(6):70-77.