带有攻击时间控制的修改比例导引法研究

陈永恒，相升海，姜登维，李 嘉，陈升富

(1.沈阳理工大学 装备工程学院，沈阳 110159； 2.辽沈工业集团有限公司 检验中心, 沈阳 110045；3.南京理工大学 能源与动力工程学院， 南京 210094)

随着现代制导理论与技术的发展，攻击时间控制制导问题正越来越受到关注[1-5]。攻击时间控制制导律目前广泛应用于联合攻击、炮火齐射等方面，通过对攻击时间的控制可实现多个导弹同时击中目标，从而提高打击效果。比例导引法因其鲁棒性和简易性而广泛应用于导弹的制导[6-7]，由于传统的比例导引法是以脱靶量为零所进行的制导律设计，并没有考虑飞行时间的约束，因此很难实现攻击时间的控制。为了能够应用比例导引法实现攻击时间的控制，研究人员在一般比例导引法的基础上结合现代控制理论，设计出能够满足控制需求，且带有传统比例导引项的制导方法，这种制导方法称为修改比例导引法。

目前，研究人员针对修改比例导引法的攻击时间控制制导问题开展研究。如文献[3]基于比例导引法中剩余飞行时间的估算和滑模控制理论，提出了修改比例导引法，实现攻击时间控制；文献[4]在研究应用比例导引法实现多个导弹联合攻击问题时，通过运用剩余飞行时间的估算，提出一种能够实现攻击时间控制的联合制导律；文献[5]采用最优控制思想，在非线性条件下提出了基于广义比例导引的攻击时间控制制导律，但并未开展深入研究，未能给出剩余飞行时间估算精度对制导律性能的影响。

本文以文献[5]的思路为基础，对非线性条件下基于修改比例导引的攻击时间控制制导律开展研究。针对基于不同剩余飞行时间估算方法下的攻击时间控制制导律，在不同初始条件和不同控制时间下进行数值仿真，探索内在变化规律及影响因素，并在此基础上分析剩余飞行时间估算精度对攻击时间控制制导律性能的影响，所得研究结果对该类制导律的实际工程应用具有一定的理论指导作用。

1 问题的描述

考虑平面内拦截静止目标的情况，其导弹和目标的运动关系如图1所示。图1中，M表示导弹，T表示目标。γ、θ、R分别表示导弹弹道角、目标视线角以及弹目连线距离。φ表示导弹前置角，aM表示制导指令，(xm,ym)表示导弹的位置，下标0表示初始条件。

假设导弹的速度VM为常值，则导弹与目标之间的相对运动关系满足如下运动学方程：

(1)

(2)

(3)

φ=γ-θ,φ(0)=φ0

(4)

导弹是通过垂直于速度方向的加速度指令进行控制。如式(3)所示，本文的加速度指令由两部分组成：第一项aB为反馈控制指令，用于减少导弹的脱靶量，实现击中目标；第二项aF为附加控制项，用于自适应攻击时间，实现攻击时间控制。

由式(2)和式(3)可得前置角的变化规律

(5)

在整个导弹导引过程中，弹目连线距R应在有限的时间内收敛到零，同时前置角φ也要收敛到零。假设在整个制导过程t∈[0,tf](其中0表示制导初始时间，tf表示制导结束时间)有|φ(t)|<π/2，则由式(1)和式(5)可得到前置角φ关于弹目连线距R的关系式

(6)

式(6)左右两端乘以cosφ，整理得

(7)

(8)

式(8)的边界条件为η(0)=0,η(R0)=η0，其中η0=sinφ0。将式(1)进行微分变换，并代入变量η有：

(9)

其中：t(R0)=0，t(R=0)是所要控制的攻击时间td。需要指出的是，所需要控制的攻击时间td应大于导弹只通过比例导引攻击目标所需的攻击时间tP。

2 攻击时间控制制导律的推导

经分析，通过直接求解非线性方程组式(8)和式(9)获得制导指令aM较为困难。为此，考虑求解一个带边界约束的最优控制问题，假设附加控制指令uF为常值，则满足方程式(8)的最优控制能量为

(10)

通过解这个最优控制问题，得到uB关于uF的方程，然后求得满足边界条件式(9)的附加指令uF。需要指出的是，关于该最优控制问题的解并不能保证实际应用于导弹的加速度指令aM的控制能量最优。

解方程式(8)和方程式(10)所组成的最优控制问题[8-9],得到以下最优解：

(11)

其中常数N定义为N=3+m, (m>-1)。当附加控制项uF为零时，反馈项aB就是比例导引法下的制导指令。

由式(11)可知，一个非零的附加控制项uF，将使导弹形成一条新的弹道轨迹，这条新的弹道轨迹摄动于由比例导引法产生的弹道轨迹，直至uF为零时，两者重合。将方程式(11)带入方程式(9)并积分，有

(12)

若将方程式(12)等号右端的第二项看做弹道轨迹曲率的控制方程，则uF可以看做是该控制方程的比例因子。

对方程式(9)进行泰勒展开并忽略高阶项有

(13)

代入方程(12)并积分有

(14)

令方程式(14)中的uF为零，得到导弹仅在比例导引法下飞行时间的估算公式如下：

(15)

解方程式(15)，可求出附加控制项uF的解析形式为

(16)

其中s(·)为符号函数

(17)

(18)

由方程式(11)和式(16)可以得到制导指令aM的最优解

(19)

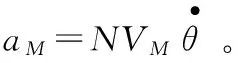
3 数值仿真和验证

3.1 剩余飞行时间估算精度验证

由式(19)可知，剩余飞行时间估算的估算精度决定着附加控制指令uF准确性，从而影响制导律的性能。为了研究剩余飞行时间估算精度对攻击时间控制制导律性能的影响，需要对不同剩余飞行时间算法的估算精度进行比较。

为获得较为精度的剩余飞行时间估算精度，将式(9)进行高阶泰勒展开，代入式(12)并令uF为零进行积分，所得高阶剩余飞行时间估算公式如下：

(20)

为验证式(20)的估算精度，在N=3,R=10 000 m，VM=300 m/s,φ0=90°的条件下，取式(20)的不同阶次解与文献[10]所提出的剩余飞行时间估算方法:

(21)

所得结果如图2所示，图2中，实际值指实际的剩余飞行时间，二阶、四阶分别指式(20)取二阶和四阶的估算值。

由图3可知，随着制导过程中前置角φ的减小，式(20)的二阶、四阶估算精度提高，且阶数越高，精度越好。而文献[10]的估算方法在整个制导过程中估算精度都较好。

3.2 制导律性能分析

为便于研究评价本攻击时间控制制导律，引入以下评价指标：控制能量J；加速度极值AM；前置角极值ΦM。分别用于表征制导过程中控制导弹所需能量，最大过载以及导弹弹道曲率。

在N=3,R=1 000 m,VM=300 m/s,γ=0°的条件下，分别对不同初始前置角φ0和不同控制时间td进行数值仿真，所得结果如表1所示。表中，PNG指比例导引法，二阶、四阶和文献10分别指用式(20)的二阶解、四阶解以及文献[10]的剩余飞行时间估算方法为基础的攻击时间控制导律，tf指导弹的实际飞行时间，无控制导指没有进行攻击时间控制的制导。

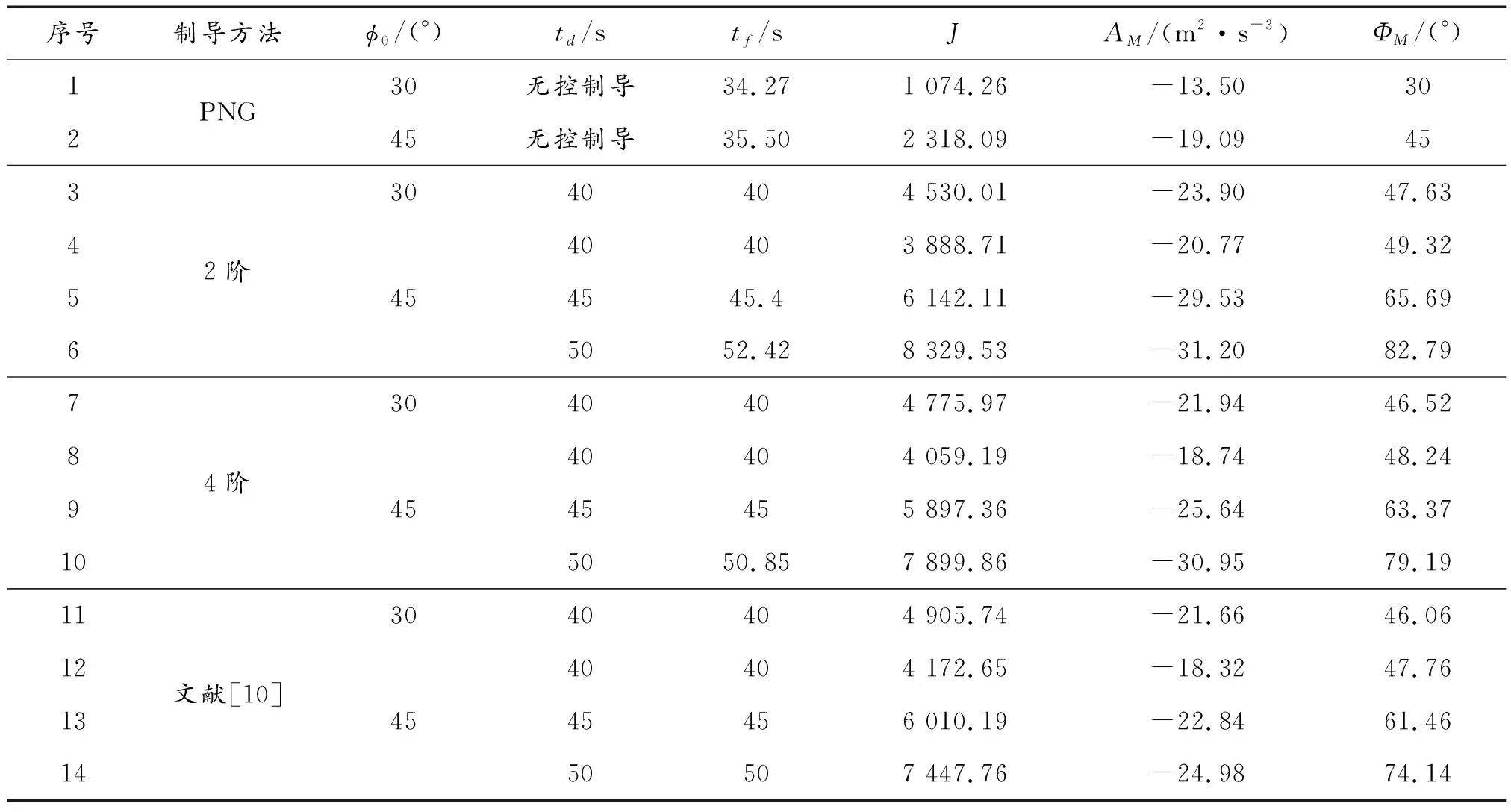
表1 不同条件下制导律的仿真结果

对比表1中的第3和第4、第7和第8以及第11和第12可知，当所需攻击时间td确定之后，初始前置角的增加将减少所需的控制能量以及制导过程中的最大过载。对比第1和第2仅由比例导引法制导的tf可知，这是由于初始前置角的增加使得攻击时间误差减小。对比表中的第4、第5、第6和第8、第9、第10以及第12、第13、第14这3组相同剩余飞行时间估算精度下的攻击时间可控范围，可以发现，剩余飞行时间估算精度越高，攻击时间可控范围越大，当剩余飞行时间估算精度不足时，将导致攻击时间控制失败，即导弹的实际飞行时间与所需控制的攻击时间不等(如第5、第6和第10)。对比表中第3、第7、第11和第4、第8、第12这两组不同剩余飞行时间估算精度下的性能评价指标可以发现，在攻击时间控制制导过程中，较为准确的剩余飞行时间估算精度所需的最大过载较小，导弹弹道曲率较小，但所需的控制能量相对较大。

图4～图7是第3和第11两种不同剩余飞行时间估算精度下的攻击时间控制制导律与相同条件下的比例导引法(第1)的制导过程中弹目连线距离、加速度指令、前置角变化以及攻击时间估算误差对比图。

由图4可知传统的比例导引法无法实现攻击时间的控制，本文所研究的攻击时间控制制导律能够较好的实现攻击时间的控制；对比图5和图6不同剩余飞行时间估算精度下的攻击时间控制制导过程中的前置角以及加速度变化指令可知较好的剩余飞行时间估算精度下，其制导过程中的导引弹道的曲率越小，所需最大过载越小。对比图6和图7可知，在文献[10]估算精度下的攻击时间误差趋向于零的速度比二阶估算精度下的要慢。这是因为较好的剩余飞行时间估算精度下，制导过程的攻击时间误差较为精确，导致制导过程中前期二阶的加速度较文献[10]的要小，而中期比文献[10]的加速度要大，从而攻击时间误差更快的趋向于零。这也是表1中相同控制条件下，剩余飞行时间估算较为准确所需的控制能量较多的原因。

4 结论

1) 攻击时间控制制导律的原理是通过附加一个与攻击时间误差和剩余飞行时间估算精度有关的控制指令uF改变基准弹道的曲率以形成新的弹道轨迹，从而实现攻击时间的控制；

2) 在相同参数条件下，剩余飞行时间的估算精度决定了在攻击时间控制制导律的攻击时间可控范围；

3) 当剩余飞行时间的估算精度越高，制导过程中的加速度极值和前置角极值越小，则所生成导引弹道的性能也越好，所需的控制能量相对较大。

[1] 马国欣,张友安.带有导引头视场限制的攻击时间控制导引律[J].弹道学报,2013,25(2):6-11.

[2] 杨哲,林德福,王辉.带视场角限制的攻击时间控制制导律[J].系统工程与电子技术,2016,38(9):2122-2128.

[3] CHO N,KIM Y.Modified Pure Proportional Navigation Guidance Law for Impact Time Control[J].Journal of Guidance Control & Dynamics,2016,39(4):1-21.

[4] JEON I S,LEE J I,TAHK M J.Homing Guidance Law for Cooperative Attack of Multiple Missiles[J].Journal of Guidance Control & Dynamics,2010,33(1):275-280.

[5] JEON I S，LEE J I，TAHK，M.Impact-Time-Control Guidance with Generalized Proportional Navigation Based on Nonlinear Formulation[J].Journal of Guidance Control & Dynamics，2016，39(8)：1887-1892.

[6] 钱杏芳,赵雅男.导弹飞行力学[M].北京：北京理工大学出版社,2012.

[7] ZARCHAN P.Tactical and strategic missile guidance[M].Progress in Astronautics and Aeronautics,6th ed.AIAA,Reston,VA,2012:13-34.

[8] BRYSON A E,JR,HO Y C,Applied Optimal Control,Hemisphere[M].New York,1975:198-241.

[9] JEON I S,LEE J I.Optimality of Proportional Navigation Based on Nonlinear Formulation[J].IEEE Transactions on Aerospace & Electronic Systems,2010,46(4):2051-2055.

[10] 陈升富,常思江.比例导引法中剩余飞行时间的计算方法[J].弹道学报,2017,29(3):14-19.