新超声速面对称飞行器制导算法仿真方法

程 胜，王 飞，陈颖瑜

(中国兵器工业第五九研究所， 重庆 400039)

超声速面对称飞行器具有快速响应、强突防能力、高机动性和高命中精度等突出优点，受到各航空航天大国的高度重视[1-2]。此类飞行器飞行速度快、飞行空域特殊，飞行过程呈现非线性、强耦合、强不确定性等与传统弹道式飞行器不一样的特性，给飞行器的研制带来巨大困难[3]。超声速面对称飞行器飞行过程中的非线性、强耦合和强不确定性对飞行器气动力(即作用在舵控制面上的控制力)的影响十分明显。气动系数一般由数值仿真或地面上的风洞试验获得，具有很大的不确定性；气动力系数受攻角、马赫数、舵偏角的一次项到高次项影响，具有强非线性，不仅如此，还包括攻角和马赫数，舵偏角和马赫数，舵偏角和攻角，舵偏角、马赫数和攻角组合高次项影响，具有强耦合性。所以，在飞行器的理论论证阶段全面考虑气动力的影响尤为重要。

制导及引导飞行器在特定的飞行条件下按照特定的要求到达目标点，特定飞行条件主要包括动压、过载、热流密度等过程约束和控制量约束，特定的要求一般为终端速度大小、速度倾角和速度方位角等终端约束。在制导算法设计完成后，通过仿真进行验证。目前在运载火箭、导弹和常规飞行器上，较常采用的仿真方法为忽略飞行器绕质心运动的三自由度仿真，该方法中的气动力计算考虑为攻角和马赫数的函数，忽略舵偏角影响。对于超声速面对称飞行器而言，传统的三自由度仿真已不能全面验证制导算法，原因如下：其一，超声速面对称飞行器所处气动环境复杂，舵偏对气动力的影响不容忽视，以美国兰利研究中心公布的超声速飞行器模型GHV[4]为例进行分析，发现舵偏对气动力的影响占30%左右。如以传统三自由度仿真方法进行超声速面对称飞行器制导算法仿真不能完全反映此类飞行器的飞行特性。其二，传统的三自由度仿真没有给出制导指令对应所需舵偏角的大小，对于仅靠舵作为执行机构进行飞行控制的超声速面对称飞行器来说，在制导算法验证时没有考虑到执行机构的承受能力，不符合工程应用要求。

基于上述背景，提出一种在仿真回路引入舵偏角的新三自由度仿真方法，并研究了舵机在回路的制导算法半实物仿真验证方法。仿真算例表明：1)本文所提新仿真方法的仿真精度与传统三自由度仿真相当，但攻角和过载的仿真结果优于传统仿真方法；2)本文给出的舵机在回路的半实物仿真方法合理，满足制导算法仿真要求，更贴近飞行器实际飞行情况，更能考验飞行器制导算法的可行性。

1 制导算法数学仿真

1.1 传统三自由度仿真

考虑地球为旋转椭球，根据文献[5]在半速度系下建立超声速面对称飞行器的质心运动模型：

(1)

式中，V为飞行器相对地球速度，θ为速度倾角，σ为从北向顺时针量起的速度方位角，r为地心距，λ和φ分别为地心经纬度，ρ为大气密度，S为飞行器参考面积，m为飞行器质量，fM为引力常数，J=1.5J2，J2为带谐项系数，ae为地球椭球体长半轴，ωe为地球自转角速度，CD、CL、CN分别为阻力系数、升力系数和侧力系数，三者都与攻角α、马赫数Ma和舵偏角δ等参数有关，该运动方程的控制量α隐含其中。另一控制量为倾侧角υ。

控制量由制导算法输出。

(2)

其中q为动压，式为其计算公式；

q=0.5ρv2

(3)

S为飞行器参考面积；CD、CL、CN分别为气动阻力系数、气动升力系数和气动侧向力系数，三者是攻角、马赫数、舵偏角和高度等参数的函数。

图1的仿真过程为：制导算法根据飞行器的当前状态r,v(位置和速度)，按一定规律解算出能导向目标的制导指令α,υ(攻角和倾侧角)，由攻角、飞行马赫数和高度(较少考虑)通过气动力模型获得飞行器在当前环境下所受的气动力F，然后结合制导算法给出的倾侧角进行飞行器三自由度运动积分计算，解算出飞行器下一时刻的飞行状态(位置和速度)。

图1 传统三自由度仿真原理图

选取合理步长，如此往复，便可仿真出飞行器完整的飞行弹道，从而验证制导算法是否满足总体要求的战术技术指标。该方法是目前各种飞行器理论研究阶段验证制导算法性能普遍采用的方法，对常规飞行器而言，打舵幅度不大，并且飞行速度低，式中气动系数中与舵偏角有关项的量级很小，在仿真时一般将舵偏角的影响忽略。

但超声速面对称飞行器飞行环境复杂，舵偏角对气动力的影响也不能忽视。在该类飞行器的气动表达式中，舵偏角及其耦合项对气动系数的贡献达30%左右。传统仿真方法忽略舵偏角影响的处理方式，导致数学计算出的气动力不能真实反映飞行器实际飞行所受的气动力，仿真结果与实际偏差较大，仿真的可信度大大降低，故传统三自由度仿真对超声速面对称飞行器制导算法的验证存在较大误差，有待改进。

1.2 新三自由度仿真

由上文分析可知，在传统的三自由度仿真中考虑舵偏角对气动力的影响至关重要。在飞行器三自由度仿真中考虑舵偏，不仅能全面模拟飞行器所受气动力，并且能兼顾到飞行器执行机构的承受能力。因此，提出一种在仿真回路中引入舵偏角的三自由度仿真方法。该方法仿真方案如图2所示，由三自由度模型、制导算法、舵偏角解算和气动力计算四部分组成，其仿真工作流程为：根据飞行器的当前状态r,v(位置和速度)，制导算法计算导向目标的制导指令α,υ(攻角和倾侧角)，舵偏角解算模块根据攻角指令计算对应的舵偏角δ，由攻角、舵偏角、飞行马赫数和高度通过气动力模型获得飞行器在当前环境下所受的气动力，然后结合制导系统给出的倾侧角进行飞行器的三自由度运动积分计算，解算飞行器下一时刻的飞行状态r,v(位置和速度)。

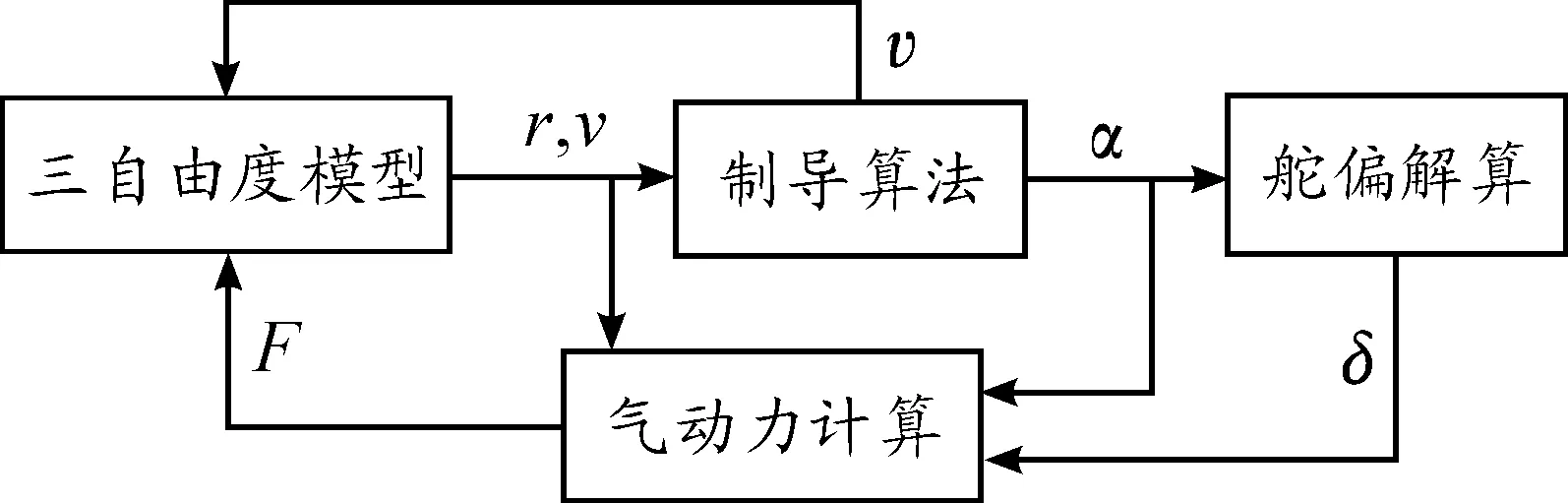
图2 新三自由度仿真方法结构图

合理的选取步长，如此往复，可仿真飞行器完整的飞行弹道，从而验证设计的制导算法是否满足总体要求的战术技术指标。该方法的难点在舵偏解算部分，其他组成部分和传统的三自由度仿真相同。

在制导研究阶段，可根据“瞬时平衡”假设建立飞行器的力矩平衡关系式：

Mst+Mc=0

(4)

式中：Mst为作用在飞行器上的气动力稳定力矩，Mc为作用在飞行器上的控制力矩。由于飞行器由气动舵提供控制力矩，故Mc=0。

将上式投影到体坐标系，展开可得：

(5)

式中Mxb、Myb和Mzb分别为滚转力矩、偏航力矩和俯仰力矩，可采用下式计算。

(6)

式中：b为翼展长度，c为平均气动翼弦，Xcg为质心到参考力矩中心距离，mx、my和mz分别为滚转、偏航和俯仰力矩系数，分别为马赫数、攻角和舵偏角等的函数。

令：

(7)

将式(6)代入式(5)中，得：

(8)

式(7)可写为：

(9)

将上式写为矩阵形式：

Aδ=B

(10)

假设A可逆，则有：

δ=A-1B

(11)

从物理意义上讲，一个攻角必然会对应一个与之配平的舵偏角，矩阵A必然可逆。如要从数学角度进行证明，需要对具体的气动模型进行具体分析。

2 制导算法半实物仿真

为了更可靠的验证制导算法的适应性和工程实用性，设计舵机在回路的半实物仿真方案，进一步验证制导算法。半实物仿真总体方案如图3所示，包括三自由度模型、制导算法、舵偏解算、舵机加载和气动力计算五部分。其仿真过程为：三自由度模型计算出飞行器当前的位置速度信息r,v；制导系统根据飞行器自身的位置、速度，结合目标的位置、速度信息给出将飞行器精确导向目标的制导指令α,υ，即攻角和倾侧角指令；舵偏解算部分解算出制导指令对应的舵偏角δc和舵机所受铰链力矩Mzjl；而后仿真计算机通过实时光纤通信系统将实时计算出的舵偏角和铰链力矩指令发送给舵机模拟器和铰链力矩模拟器，进行铰链力矩加载和舵偏角复现，待舵机加载完成后，高精度传感器对实际舵偏δ进行采集；气动力计算根据马赫数、攻角和实际舵偏角的大小计算飞行器所受气动力F，然后三自由度模型进行下一步仿真计算，直至仿真结束。

图3 制导算法半实物仿真方案图

舵偏加载部分可采用真实舵机或舵机模拟器进行舵偏加载，并适时模拟舵机在飞行中所受的铰链力矩。下面给出铰链力矩的计算模型。

铰链力矩为作用在舵控制面上的控制力(通常为气动力)对舵铰链轴产生的力矩。其大小可通过理论计算、工程估算或实验测试获得。影响铰链力矩的因数很多，为简化研究，主要考虑飞行攻角引起的上洗(攻角变化引起舵面上法向力的变化)和舵偏角引起的面-面干扰[6]，文献[7]将铰链力矩展开为：

(12)

在式(12)的基础上，参考文献[8]，可建立一种与气动力系数计算方法类似的铰链力矩计算模型，通过力矩系数描述为：

(13)

根据上述半实物仿真方法可搭建图4所示的制导算法半实物仿真系统。整个实验系统有四大组成部分，分别为仿真计算机、角度加载控制柜、力矩加载控制柜和舵机系统。仿真计算机、角度加载控制柜和力矩加载控制柜之间通过VMIC光纤反射内存网连接，组成一个环形结构。角度加载控制柜、力矩加载控制柜和舵机系统之间通过传输线连接。

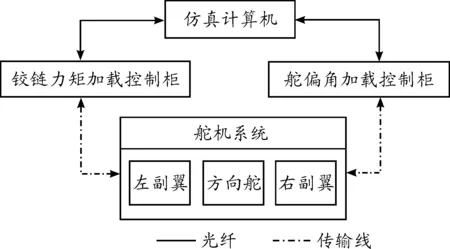
图4 半实物仿真实验系统组成简图

3 仿真算例

仿真采用美国NASA兰利研究中心公布的GHV(Generic Hypersonic Vehicle)总体和气动模型[4]。选取飞行起点：高度25 km，经纬度(1°，1°)，飞行速度2 000 m/s，速度倾角为0°，速度方位角为-40°。取目标点：经纬度(1.4°，1.4°)，终端速度倾角γDF=-70°。整个飞行阶段攻角范围为0≤α≤20°，攻角变化率不超过5 °/s，倾侧角变化率不超过20 °/s，最大过载为20 g。为了验证本文所提仿真方法的可行性，选取经典的最优比例制导律[5]作为制导算法进行仿真验证，与其传统的仿真结果进行对比。

3.1 新仿真方法与传统仿真对比分析

在完全相同的条件下，采用C++编程语言，分别进行两种数学仿真方法的编程计算，仿真结果如图5所示。图中TSM(Traditional Simulation Method)为传统仿真方法，NSM(New Simulation Method)为本文所提新仿真方法。两种方法的仿真步长均为0.001 s。

图5(a)、(b)、(e)表明，新仿真方法和传统三自由度仿真方法一样，都能在满足终端约束下精确命中目标。说明新仿真方法切实可行，能达到检验制导律的目的。

新仿真方法和传统三自由度仿真方法二者的弹道特性却有区别，放大图5(b)可以看出，在俯冲开始段，新方法弹道的曲率半径比传统仿真稍大，但不明显。

在俯冲中段至末端攻击段，新方法弹道的曲率半径明显小于传统仿真。新方法弹道的优点在于随着弹道曲率半径的减小，飞行器飞行所需攻角显著减小，弹道对飞行器的控制能力要求比较低，飞行器容易控制，攻角显著减小，由图5(c)显而易见。

另外，随着弹道后半段曲率半径的减小，飞行器承受的过载显著减小，特别是在攻击末段，过载大幅减小，这从图5(f)可以得到证明。

图5(g)为本文新仿真方法所解算出的舵偏角，可见飞行器的左右副翼舵偏基本一样，方向舵偏为0，不起作用。说明制导算法解算出的舵偏角只包含了攻角作用项，没有体现倾侧角。这与“瞬时平衡假设”相吻合，证明舵偏解算正确。

综上可知，本文提出的高超声速飞行器新仿真方法优于传统仿真方法，具有参考价值。下面通过半实物仿真实验来进行进一步验证。

3.2 半实物仿真与数学仿真对比分析

在上文设计的半实物仿真方案和给出仿真条件下，利用图5搭建的半实物仿真系统开展半实物仿真。半实物仿真的仿真步长为100 ms。将半实物仿真的结果与数学仿真的结果进行对比分析，如图6所示，图中HILS(Hardware-in-the-loop Simulation)为半实物仿真结果，MS(Mathematical Simulation)为数学仿真结果。由图5(g)知数学仿真时，方向舵偏角为0，故在半实物仿真时不考虑方向舵偏角；又左右副翼舵偏角一样大，在实验时选右副翼舵偏角进行仿真研究。

图6(a)-(c)表明半实物仿真结果和数学仿真结果相一致，半实物仿真在接入真实舵偏的情况下依然能精确的命中目标，说明本文设计的半实物仿真方案可行，本文所考核的制导算法能满足制导任务要求。图6(g)(h)给出了右副翼舵偏角的半实物仿真结果和数学结果和其对应的铰链力矩。可以看出，半实物仿真的铰链力矩在较小值时有抖动，这是由于试验设备之间存在误差，造成了相应舵偏的颤振，图6(h)中虚线的前面部分印证了这一点。图6(d)(e)给出了半实物仿真和数学仿真的控制量变化情况，可以看出，两者的控制变化高度一致，这说明即使在仿真开始舵偏角有一定抖动时，制导算法还是能通过自身的鲁棒性进行克服。图5(f)为过载变化，整个半实物仿真过程中，过载大小与数学仿真无差别，满足飞行器结构上的约束。

4 结论

1) 仿真结果表明本文所提新仿真方法仿真得到的攻角和过载结果比传统方法显著减小，利于在飞行器控制系统设计时充分利用其控制能力，可为面对称飞行器的理论研究与型号论证等阶段提供很好的验证途径。

2) 舵机在回路的半实物仿真方法可在仿真回路中充分考虑飞行器控制系统执行结构的实际响应能力，比数学仿真更贴近飞行器真实飞行情况，更能考验飞行器制导算法的可行性，可为理论研究者或者工业部门提供参考。

[1] 韩洪涛,王友利.2013年国外高超声速技术发展回顾 [J].中国航天,2014(3):16-20.

[2] XU MingLiang,CHEN KeJun,LIU LuHua,et al.Quasi-equilibrium glide adaptive guidance for hypersonic vehicles[J].SCIENCE CHINA:Technological Sciences,2012,55(3):856-866.

[3] WANG Peng,TANG Guo-jian,LIU Lu-hua,WU Jie.Nonlinear hierarch-structured predictive control design for a generic hypersonic vehicle[J].Science China Technological Sciences,2013,56(8):2025-2036.

[4] SHAUGHNESSY J D,PINCKNEY S Z,MCMINN J D,et al.Hypersonic vehicle simulation model winged-cone configuration[R].NASA Technical Memorandum 102610,1990.

[5] 赵汉元.飞行器再入动力学和制导[M].长沙:国防科技大学出版社,1997.

[6] 汪令羽.全动控制舵铰链力矩计算方法研究[J].北京理工大学学报,1996,16(4):444-449.

[7] YOONSU NAM,JINYOUNG LEE,SUNG KYUNG HONG.Force Control System Design for Aerodynamic Load Simulator[C]//Proceedings of the American Control Conference.Chicago,2000.

[8] 鲁建,李邦清,刘永远.一种用舵反馈信号计算铰链力矩的方法[J].战术导弹与控制技术,2006,52(1):84-85.