硝酸羟胺基单组元发动机起动过程数值模拟

孙得川，金东洙，于泽游

(大连理工大学航空航天学院，工业装备结构分析国家重点实验室， 辽宁 大连 116024)

单组元液体火箭发动机系统简单、可靠性高，广泛应用在空间飞行器上[1]。我国现有型号的单组元发动机大多采用无水肼作为推进剂，它不仅昂贵、易燃、易爆，而且有剧毒，不利于人员操作，因此新型无毒单组元发动机是当前单组元火箭发动机的主要研制方向之一。无毒单组元推进剂包括过氧化氢、氧化亚氮、硝酸羟胺(HAN)基、二硝酰胺铵(ADN)基、和硝酸烷基酯类(如硝酸异丙酯，IPN)的推进剂等[2-7]。目前对无毒推进剂单组元发动机的研究主要集中在推进剂的催化分解研究和推进剂性能实验研究方面。例如，Amrousse[7-8]、Katsumi[9]、Chang Hwan Hwang[10]等人对AND和HAN基推进剂的热分解和燃烧进行了研究；陈永康[11]、潘玉竹[12]、任晓光[13]分别对HAN基液体推进剂的热分解动力学、高压燃烧特性和催化分解进行了研究。对于无毒单组元发动机工作过程的研究相对较少，其中主要是通过热试车对无毒单组元发动机的比冲、起动特性等做一些宏观的测试[14,15,16]，缺乏对单组元发动机工作的物理过程的理解。单组元发动机的仿真重点在于催化室内的物理和化学过程。虽然针对催化床内的流动和传热的仿真研究不少[17-21]，但是这些研究主要是针对一般工业中的催化床，无法直接将其方法和结论应用于单组元火箭发动机。因此，本文通过对某一HAN基推进剂单组元发动机进行起动过程和稳态工作过程的仿真研究，旨在探讨适用于单组元发动机的仿真方法，并加强对单组元发动机内部流动与传热过程的理解。

1 计算模型

发动机的催化床中堆积了数量众多的催化剂颗粒，直接对颗粒间的流动和传热进行仿真很困难，所以本文将催化床简化为多孔介质进行计算，采用如下假设：

1) 前、后催化床均简化为多孔介质区域，忽略催化床前、后的多孔隔板；

2) 不考虑推进剂的分解过程，认为推进剂在进入催化床后完全分解；

3) 推进剂从喷注器均匀流入催化床；

4) 只考虑催化床内气相的流动及气相和固相间的传热；

5) 催化床的物理性质各向同性；

6) 发动机外壁面只考虑辐射换热。

本文应用FLUENT软件进行计算。仿真求解的气相方程为不带化学反应的多组分N-S方程。气体成分为推进剂催化反应后的冻结组分，其性质(如理论温度、分子量、粘性系数等物性参数)通过化学平衡计算给出。催化床内的流动主要依据多孔介质流动的Ergun方程[22]。多孔介质内的传热采用non-equilibrium模型，即气相和固相的温度不同，两者之间存在换热。催化室前床和后床的孔隙率、惯性阻力系数、粘性阻力系数和对流换热系数根据催化床参数进行计算。

计算采用基于压力的分离算法；压力修正采用SIMPLE方法；其他物理量的空间差分采用二阶精度的迎风格式。湍流模型采用标准k-ε模型。对于起动过程，时间推进采用非定常的隐式二阶精度格式进行求解(双时间法)。

1) 流体控制方程

在流体计算中，连续方程、能量方程和动量方程表示成统一的形式：

(1)

式中：φ为通用变量，Γ为广义扩散系数，S为广义源项。

2) 多孔介质的动量方程

多孔介质对流体的作用通过动量源项在流体动量方程中体现，该源项包括粘性损失项和惯性损失项。第i个动量方程中的源项Si表示为：

(2)

方程右端第一项是粘性损失项，第二项是惯性损失项，D和C是给定的矩阵。对于均匀的多孔介质，

(3)

(4)

式中：Dp为催化剂颗粒的直径，ε为催化床的孔隙率。

3) 多孔介质能量方程

多孔介质模型对能量方程的影响体现在对时间导数和对流项的修正上，时间导数中，引入了固体区域对多孔介质的热惯性效应，能量方程如下：

(5)

4) 多孔介质中流固耦合传热

多孔介质中，气相与固体的交界面处应该满足能量守恒，即

(6)

式中：λ为固体的导热系数，h为流体的对流换热系数(根据文献[23]计算)，T为温度，n为壁面的法向方向，下标f和s分别表示流体和固体。

2 计算条件

2.1 发动机参数

计算对象为某HAN基推进剂单组元试验发动机。试验测得该发动机的稳态工作压强(绝对压力)Pc=0.72 MPa。

发动机推力室结构如图1所示。其中催化室由前床和后床组成；壳体材料为高温合金GH1131。图中T1、T2、T3点为试车时发动机外壁面的测温点。

催化剂颗粒材料为含铝氧化物。表1给出了催化剂颗粒的相关参数，从表1中计算出前床的孔隙率为ε=0.3，后床的孔隙率为ε=0.375。

2.2 计算网格及边界条件

图2所示为对发动机简化后的二维轴对称计算网格，整个计算域网格总数为18 758个单元，其中流场计算域的网格为16 790个单元，固体计算域的网格数1 968个单元。

表1 前、后床颗粒的物性参数

推进剂入口边界条件采用流量入口。根据试验数据，拟合得到流量与时间之间的关系式：

qm=100.97t-6 605.90t2+189 982.62t3-

1 491 000t4+2 650 870t5-0.31 g/s

时间t的值为0～0.154 s，大于0.154 s后发动机的流量为30 g/s。根据上式编写UDF作为流量进口的边界条件。出口边界条件为压力出口，设置为试验时的环境压强值(100 Pa)。发动机的外壁面为辐射边界条件，辐射系数取0.5，环境温度假定为300 K。

在时间推进的双时间法中，时间步长和时间步长内迭代的次数影响计算稳定性和准确性；经过试算验证，本文中时间步长取为1×10-6s，内迭代次数取为30次，保证每个时间步长内残差基本收敛到稳定值。

2.3 热力计算

因为HAN推进剂的催化反应十分的复杂，故本文计算中假设推进剂分解后的气体为化学平衡组分，采用热力计算的方法对燃气成分和发动机理论性能进行计算。

热力计算时，推进剂的配方依据发动机性能和参考文献[24]，假定为63.2%硝酸羟胺(HAN)，20.0%三乙醇胺硝酸盐(TEAN),16.8%水(H2O)。

表2列出了根据化学平衡计算结果得到的燃气组分数据(略去摩尔含量小于1%的组分)：

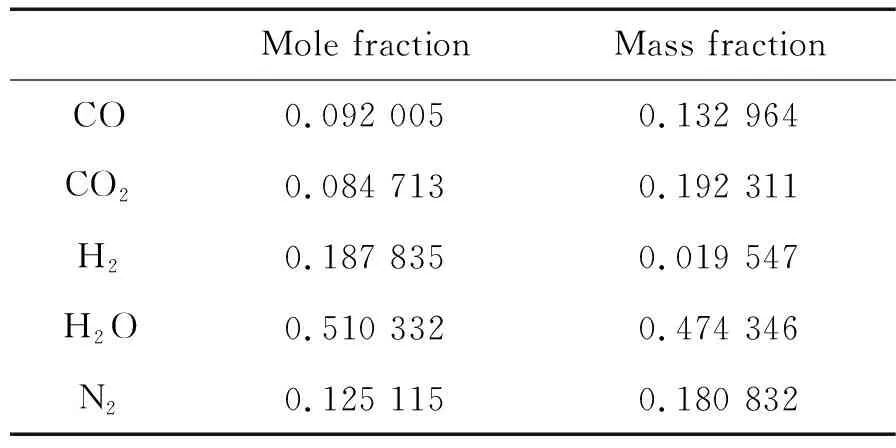
表2 燃气成分

通过热力计算得到了燃气平均分子量为19.382，气体常数为428.979 J/(mol·K)，动力黏性系数为5.397×10-5Pa·s，导热系数为0.209 1 W/(m·K)；燃气温度为1 587 K，发动机的理论比冲为228.1 s。

3 计算结果讨论

本文计算了发动机的起动过程和稳态工作过程，并将计算结果与试验测量结果进行了对比。在发动机试车前，在发动机外壁的不同位置布置3个热电偶用于测量外壁面温度变化(热电偶的位置如图1所示)，同时在电磁阀门上游及催化床下游布置压力传感器用于测量压力变化。

3.1 起动过程

在HAN基推进剂发动机试车时，需要对催化床进行预热，以使推进剂能够顺利分解，催化床的有效预热温度为120 ℃。本文计算中，将计算区域的初始温度统一设置为120 ℃。

图3反映了起动过程中推力室对称面上的温度变化，图4为t=2 s时其内部燃气和催化床的轴向温度曲线。

观察这两图可知，催化床的升温过程包括两个方面：一是催化床整体的温度在高温热解气体的传热作用下逐渐升高；二是高温从催化床上游逐渐向下游传递。从温度分布上看，催化床上游温度高于下游，另外催化床内部靠近轴线位置的温度也高于壁面附近温度，即在催化床内不仅存在轴向温度梯度，也存在径向温度梯度。此外，由于推力室壳体向外界的辐射传热，使得壳体温度显著低于催化室温度。

需要指出，因为本文的计算模型没有考虑液体推进剂分解成为高温燃气的过程，所以计算得到的温度在喷注器处呈现最大值，这与实际情况并不相符。实际状态应该是喷注器处的温度等于或略高于液体推进剂温度，而后在下游液相分解反应时迅速升温。

图5给出了某次试验的发动机外壁温度变化，所示实验值为图1中T1处的温度值。从试验曲线看到，因为热量传递到壁面处需要一定时间，所以0～1 s的温度变化很小；当壁面温度开始上升时，其升温速率基本呈线性。本文计算了外壁面辐射系数为不同值时的外壁面升温曲线，对比试验数据可知当热辐射系数设置为0.4时，计算得到的升温速率和试验值接近。

图6给出了起动过程中推力室的温度变化过程(测点位于催化床下游的燃烧室内，距内壁面0.5 mm)。从图6可知：(1)起动时燃气流过催化床的时间大约为0.094 s；(2)高温燃气在催化床内流动时向催化床颗粒传热，流出催化床时温度较低，起动初期小于200 ℃，而后随着时间推移逐渐升高，说明催化床的温度也在升高，燃气与催化床之间的换热量逐渐减小。

图7给出了起动过程中推力室的压力Pc变化过程(测点位于催化床下游，距内壁面0.5 mm，与图5的温度测点相同)。可见，计算得到的升压过程曲线与试验曲线较为吻合，但计算的稳态值略高于试验值。另外，升压过程存在比较明显的拐点(图7中示出了拐点坐标)，在拐点前压力上升非常快，而后则呈现缓慢爬升。升压过程的这种表现具有单组元发动机的典型特点，与参考文献[25]描述的肼发动机基本一致：即以压力曲线的拐点为界可将升压过程分为两个阶段；前面升压快的部分对应着燃气充填推力室的过程，燃气在这个阶段中迅速充满推力室并使喷管达到壅塞流动状态，但是因为燃气向催化床传热，使燃气热能损失较大，导致拐点压力并不高；而后面升压慢的部分则对应着催化床的升温过程，在这个阶段中随着燃气对催化床的传热，使催化床温度逐渐升高，进而燃气的热损失逐渐减小，压力进一步升高。因为催化颗粒的热容较大，所以催化床温度上升较慢，升压过程的第二阶段时间较长。此外，在升压曲线中没有起动峰值出现，说明催化床的催化效能较好，没有产生推进剂积存现象。

从计算结果来看，升压曲线拐点的出现比试验值早了约0.11 s，这是因为计算没有考虑推进剂的分解过程。计算的拐点压力值与试验值非常接近，且稳态压力的计算值与试验值也比较吻合，这说明采用化学平衡计算得到的燃气参数与实际燃气比较符合。

3.2 稳态工作过程

发动机稳定工作时，流场中的参数基本不再发生变化。图8和图9给出了推力室对称面上的压力分布云图和沿着对称轴的压力分布。由于催化床为多孔介质，其孔隙率影响床内压降，因前床的孔隙率较小所以压降较大，后床的孔隙率较大所以压降较小，这在压力分布图中得到了较好的体现。另外，从计算可得催化床下游的室压计算值约为0.77 MPa，高于试验值(0.72 MPa)约7%。计算值高于试验值的原因，主要由于计算中没有考虑反应效率，认为催化反应处于平衡状态；另一个原因是催化床的压降小于实际压降，这就需要调整流阻系数。

图10给出了温度分布云图，从图10可以看出推力室的最高温度约为1 580 K；收敛段部位的燃气温度为1 300～1 400 K；从推力室下游到喷管出口温度一直下降。由于发动机壳体向外热辐射，所以壳体温度低于燃气温度。此外，壳体在喉部的温度高于其他部位，这一方面是因为喉部壳体与燃气的对流换热系数大，另一方面也是喉部表面积小，向环境辐射的热量少。

图11给出了轴向速度的幅值分布，通过对喷管出口的动量和压差进行积分得到计算的比冲为224 s，与理论计算值(228.1 s)接近。

4 结论

1) 采用本文建立的计算模型和模型参数计算方法，可以对单组元液体发动机进行工作过程仿真，仿真得到的升压曲线和外壁温度与试验结果符合较好。

2) 催化床承载了较大的压降，且压降受孔隙率影响很大；前催化床孔隙率略小，所以前催化床压降明显大于后催化床压降。

3) 单组元发动机起动过程中，室压上升曲线分为两个阶段，第二阶段时间长于第一阶段。

4) 当计算模型中不考虑液体推进剂的反应过程时，计算得到的初期升压速率快于实际情况。

[1] 周汉申.单组元液体火箭发动机设计与研究[M].中国宇航出版社,2009.

[2] 白云峰，林庆国，金盛宇，等.过氧化氢单元催化分解火箭发动机研究[J].火箭推进,2006,32(4):15-20.

[3] 宋长青,徐万武,张家奇,陈健.氧化亚氮推进技术研究进展[J].火箭推进,2014,40(2).

[4] 禹天福，贾月.一氧化二氮催化分解的研究与应用[J].化学推进剂与高分子材料,2006,4(2):6-10.

[5] 周悦,公绪滨,方涛.硝酸羟铵基无毒单组元推进剂应用探讨[J].导弹与航天运载技术,2015(4).

[6] SHUTARO NISHIKIZAWA,TAKEHIRO OHIRA,HIRONORI SAHARA.Development of Mono /Bi-Propellant Propulsion System for Microsatellites and Planning of Space Demonstration[C].49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference,San Jose,CA,2013.

[7] AMROUSSE R,HORI K,FETIMI W,et al.HAN and ADN as liquid ionic monopropellants:Thermal and catalytic decomposition processes[J].Applied Catalysis B:Environmental,2012,127:121-128.

[8] AMROUSSE R,KATSUMI T,AZUMA N,et al.Hydroxylammonium nitrate (HAN)-based green propellant as alternative energy resource for potential hydrazine substitution:From lab scale to pilot plant scale-up[J].Combustion and Flame 2017,176:334-348.

[9] KATSUMI T,INOUE T,NAKATSUKA J,et al.HAN-Based Green Propellant,Application,and Its Combustion Mechanism[J].Combustion,Explosion,and Shock Waves 2012,48(5):536-543.

[10] CHANG HWAN HWANG，SEUNG WOOK BAEK，SUNG JUNE CHO.Experimental investigation of decomposition and evaporation characteristics of HAN-based monopropellants[J].Combustion and Flame,2014,161:1109-1116.

[11] 陈永康,陈也弘,安振涛,等.HAN-基凝胶推进剂的热分解反应动力学[J].火炸药学报,2016,39(4):77-81.

[12] 潘玉竹.HAN基液体推进剂高压燃烧特性的实验研究和数值模拟[D].南京:南京理工大学,2013,4.

[13] 任晓光.硝酸羟胺基推进剂的催化分解研究[D].大连:大连轻工业学院,2006.

[14] CHEN Jun,LI Guoxiu,ZHANG Tao,et al.Experimental investigation of the catalytic decomposition and combustion characteristics of a non-toxic ammonium dinitramide (ADN)-based monopropellant thruster.Acta Astronautica,2016，129:367-373.

[15] ZHANG Tao,LI Guoxiu,YU Yusong,et al.Numerical simulation of ammonium dinitramide (ADN)-based non-toxic aerospace propellant decomposition and combustion in a monopropellant thruster[J].Energy Conversion and Management,2014,(87):965-974.

[16] 李华乐.ADN/甲醇推进剂燃烧反应动力学模型及推力器燃烧过程仿真的研究[D].北京:北京交通大学,2014.

[17] GUARDO A.,COUSSIRAT M.,RECASENS F,et al.CFD studies on particle-to-fluid mass and heat transfer in packed beds:Free convection effects in supercritical fluids[J].Chemical Engineering Science，2007,62：5503-5511.

[18] GUARDO A,COUSSIRAT M,RECASENS F,et al.CFD study on particle-to-fluid heat transfer in fixed bed reactors:Convective heat transfer at lowand high pressure[J].Chemical Engineering Science，2006,61:4341- 4353.

[19] 郭雪岩.CFD方法在固定床反应器传热研究中的应用[J].化工学报,2008,59(8):1914-1922.

[20] KAMIUTO K,SAITOH S.Simultaneous Heat and Mass Transfer in Packed Bed Catalytic Reactors[J].Journal of Thermophysics and Heat Transfer,1995,9(3):524-530.

[21] ZHOU X,HITT D L.Numerical Modeling of Monopropellant Decomposition in a Micro-Catalyst Bed[C].35th AIAA Fluid Dynamics Conference and Exhibit,2005(6):1-10.

[22] ERGUN S.Fluid flow through packed columns [J].Chemical Engineering Progress,1952,48:89-94.

[23] 郑坤灿,侯戎彬,王景甫,等.基于孔喉模型的多孔介质对流换热系数的分形研究[J].科学技术与工程,2014,14(28):44-49.

[24] 王宏伟,王建伟.AF-315液体单元推进剂研究进展[J].化学推进剂与高分子材料,2010,8(5):6-9.

[25] SCHMITZ B W,SMETH W W.Development of Design and Scaling Criteria for Monopropellant Hydrazine Reactors Employing Shell 405 Spontaneous Catalyst[R].RRC Report 66-R-76,1967,11(1).