基于成岩储集相分类的致密储层孔隙度建模

周游, 景成, 李治平, 张志营

(1.中国地质大学(北京)能源学院, 北京 100083; 2.非常规天然气能源地质评价与开发工程北京市重点实验室,北京 100083; 3.西安石油大学石油工程学院, 陕西 西安 710000; 4.中国石化东北石油局, 吉林 长春 130000)

0 引 言

对于低渗透率、特低渗透率等致密砂岩储层,沉积作用是其形成的基础,但复杂的成岩作用最终决定着储层的储集性能[1-2]。以往研究大多数以沉积作用、流动单元、岩石物理相等作为孔隙度的主控因素建模为主[3-5]。这些孔隙度解释模型离散点较多,分类模型中数据点集中趋势不明显。因沉积作用是储层形成的基础,而成岩作用则是在原始沉积的基础上对储层物性产生更大的影响,并最终决定了内部储集空间的特征,直接影响到孔隙空间的形成和演化[6-8]。

本文以苏里格气田东区盒8上致密储层孔隙度为例,通过分析该区储层不同类别成岩储集相基本特征,阐明成岩储集相是孔隙度变化的主控因素,建立起基于成岩储集相分类的孔隙度测井解释模型,精确表征该类储层的孔隙特征。

1 分类成岩储集相综合特征

对于苏里格东区上古生界盒8上期曲流河沉积致密气储层,其沉积物分选差,研究区内储层微观孔隙类型多样且结构异常复杂,孔隙度和渗透率关系复杂多变,具有极强的非均质性[9-10]。

不同成岩作用的强弱决定了孔隙结构和孔隙演化的复杂程度[11-13]。按对储集性能的影响,可以把成岩作用分为建设性和破坏性成岩作用。其中溶蚀作用、广泛发育的破裂缝为建设性成岩作用,有利于成岩储集相的形成。压实与胶结作用则不利于成岩储集相的形成和演化,均为破坏性的成岩作用。通过对研究区孔隙度演化过程进行反演[14],得到不同类型岩相在成岩演化过程中孔隙度演化规律和演化参数变化,据此将该区成岩储集相分为4类。

强烈的压实和胶结作用是形成该区低孔隙度的关键因素。Ⅰ、Ⅱ类成岩储集相成岩过程孔隙参数演化反映了相对较低胶结、压实及相对较强溶蚀作用特征,具有相对较好的储渗条件及孔隙结构特征,溶蚀作用增大孔隙度可达10%以上。Ⅲ、Ⅳ类成岩储集相成岩过程孔隙参数演化表现出相对高压实、胶结和弱溶蚀作用特征,形成了该区复杂多变的孔隙结构,储渗能力较差。不同成岩储集相带其成岩过程中孔隙度演化特征明显不同,而同种类别成岩储集相其孔隙度成岩演化模式趋于一致,进一步验证了分类成岩储集相对该区致密气储层孔隙度变化具有主要的控制作用[15]。

硅质胶结和高岭石胶结是研究区典型的成岩现象。大量研究结果表明,该区硅质胶结岩相的储集性能远好于高岭石胶结岩相。进一步综合孔隙度演化模式图,依据该区成岩储集相形成的地质条件,基于镜下薄片鉴定和物性资料,在研究区划分出Ⅰ类优势型(硅质弱胶结-溶蚀型)、Ⅱ类较好型(硅质胶结型)、Ⅲ类较差型(高岭石胶结型)和Ⅳ类致密型(强压实胶结型)4种类型成岩储集相(见表1),它们是岩石在不同沉积期所经历的各种成岩作用对其进行改造叠加所最终形成的综合产物[16]。

2 成岩储集相测井多参数定量综合评价

成岩储集相的划分要依靠详细的岩心数据信息和分析化验资料,但在油田勘探开发中这些资料十分有限,因此把测井所采集的大量信息系统有序地转化为分类成岩储集相的识别评价方法非常必要。但是,利用任意单一测井参数均不能准确划分类别,为此采用灰色理论的分类原则和处理方法,综合各项测井参数对该区盒8上成岩储集相进行归纳和统计,利用其平均数据列作为成岩储集相的评价划分指标[17]。采用准确率及分辨率联合分析赋予每一个评价指标以不同的权系数[18],以此建立起该区成岩储集相评价划分标准及权系数(见表2)。

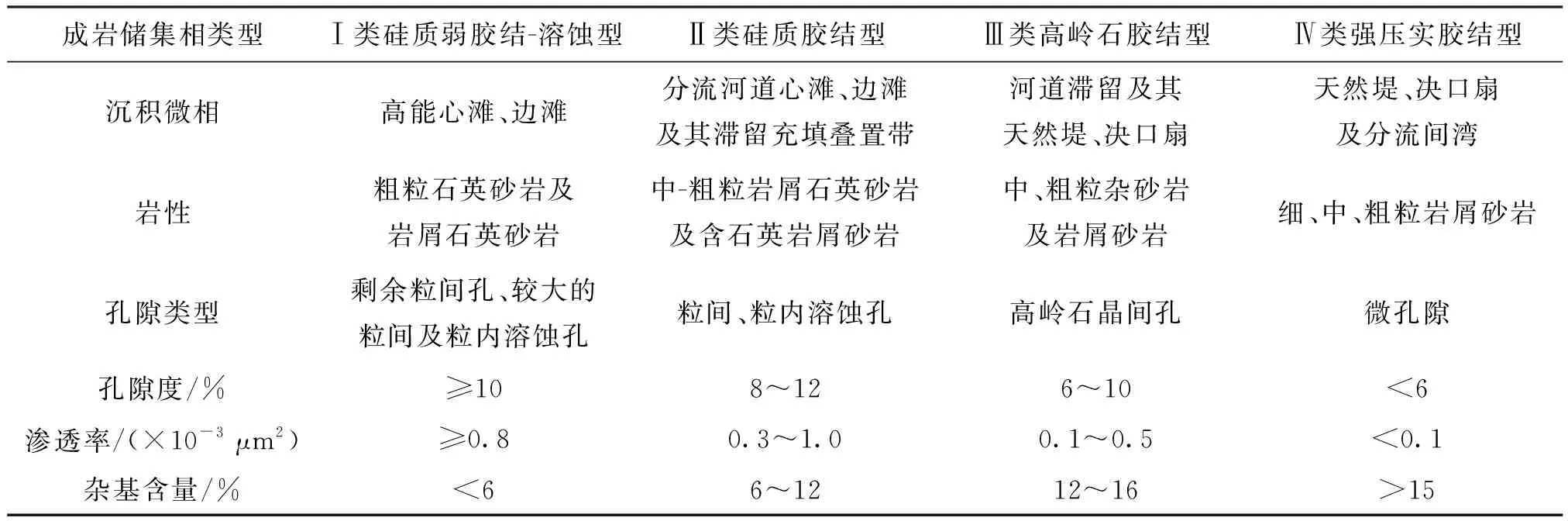
表1 研究区盒8上致密气藏成岩储集相分类特征参数统计表

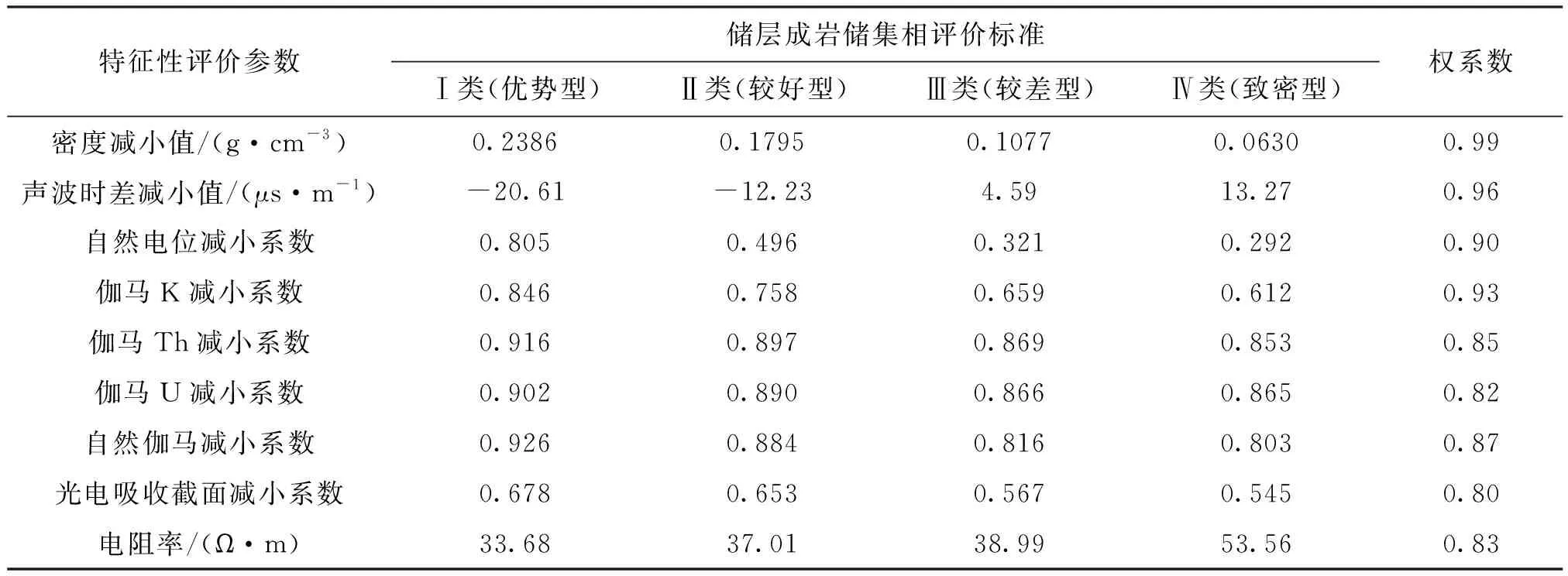
表2 成岩储集相测井多参数综合评价指标体系

为评价表2中各类成岩储集相类型,根据该区未取心层段60多个层点的测井参数统计结果,利用灰色理论综合评价方法,分别对上述9种评价指标进行被评价井点数据的综合分析及处理,采取最大隶属原则作为判别成岩储集相的结论[19]。将此划分法推广应用到非取心层段,实现了全区成岩储集相的综合评价。为验证其准确性,利用该体系对该区未参与测井参数评价标准建立的取心已知样品进行判别,准确率为97%,能取得满意的结果。

3 致密气储层孔隙度多参数联合建模

通过探究不同类型成岩储集相孔隙度系列测井响应参数与其岩心分析孔隙度的关系,发现声波时差和密度与其岩心分析孔隙度拟合效果最好,分类模型数据点具有相对集中的分布趋势及较为明显的线性关系,而中子孔隙度由于致密气储层的挖掘效应致使其拟合效果较以上2种稍为分散。但这3种分类模型所计算出的孔隙度都具有其各自的合理性,同时也反映了各自的成岩储集相特征(见表3和图1至图3)。表3中ρb、Δt、φN分别为密度、声波时差及中子孔隙度的测井值。

图1至图3为分类成岩储集相岩心分析孔隙度与密度、声波时差及中子孔隙度关系图。可以看出经成岩储集相分类后建立的孔隙度模型其对应关系较为吻合,不同程度地反映了各自成岩储集相的分类特征。同时随着成岩储集相类别由优势型变为致密型的过程中,岩心分析孔隙度随密度、声波时差的变化率都有变缓的趋势。这是由于随着储层岩性、物性的变差,储层越来越致密,其测井响应来自于储层孔隙中的信息量变少,故其孔隙度随测井响应参数的变化也相应有所降低。由分类成岩储集相建立的孔隙度模型改善了分类模型数据点的线性关系及其均匀程度,在一定程度上克服了采用统一模型进行计算造成的低分辨率的评价误差。

表3 致密气储层不同成岩储集相测井解释孔隙度模型

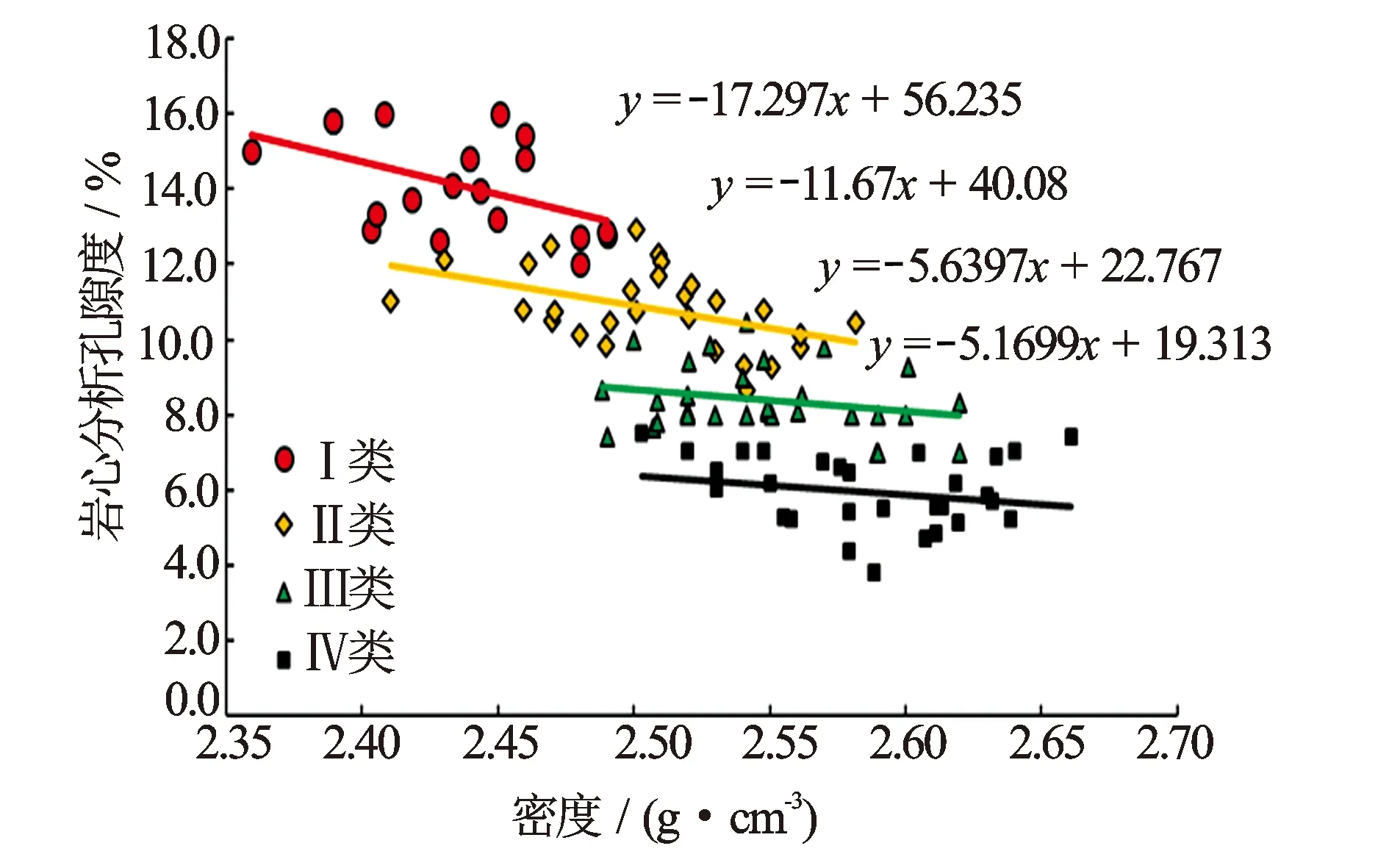
图1 分类成岩储集相岩心分析孔隙度与密度关系图

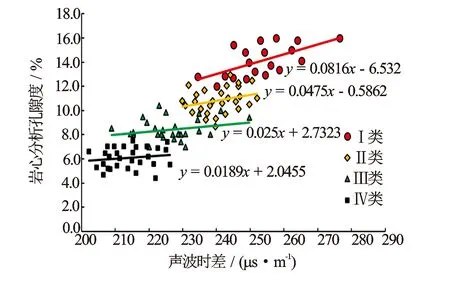
图2 分类成岩储集相岩心分析孔隙度与声波时差关系图

图3 分类成岩储集相岩心分析孔隙度与中子孔隙度关系图

密度、声波时差及中子孔隙度测井曲线都能从不同角度、不同程度反映储层的孔隙结构和特征。为此,采用密度、声波时差及中子孔隙度联合求取孔隙度参数解释模型,可以很好兼顾每个评估值,较大限度地减小偏离量大的数据点对测量结果的影响,能更为准确地综合各类信息来求取不同成岩储集相孔隙度参数值。

将Ⅰ类型成岩储集相岩心分析孔隙度数据列及利用密度、声波时差及中子计算出的与其相对应孔隙度的数据列排列成n×4矩阵为

[A0(k),A1(k),A2(k),A3(k)]

(1)

式中,k=1,2,3,4,为成岩储集相类型;n为岩心分析或计算数据点的个数;A0(k)为岩心分析孔隙度数据列;A1(k)、A2(k)、A3(k)分别为利用密度、声波时差及中子孔隙度计算出的孔隙度数据列。

采用偏差度表示每种孔隙度建模方法的计算结果与真实岩心分析孔隙度值之间的接近程度

(2)

采用离散度表征每种建模方法其计算结果的离散程度

(3)

可知各解释模型与真实岩心分析孔隙度之间的偏差度和其各自离散度越小,表示其计算结果更为接近实际情况。每种解释模型的相关系数Ri(k)也能反映计算结果拟合的相关程度及其合理性,相关度越大,拟合效果越好。

故采用偏差度、离散度和相关度联合建立起评价方法的权系数为

(4)

最后,对评价方法的权系数进行归一化处理

(5)

以此建立起分类成岩储集相测井解释孔隙度模型各种建模方法的4组权系数{qi(1),qi(2),qi(3),qi(4)}(见表4)。

由前可知,密度、声波时差及中子孔隙度求取孔隙度模型可分别写成

φ1=A1ρb+B1

(6)

φ2=A2Δt+B2

(7)

φ3=A3φN+B3

(8)

式中,Ai、Bi为常数。设密度、声波时差及中子孔隙度参数在孔隙度建模中的权系数分别为q1(k)、q2(k)、q3(k),则分类成岩储集相孔隙度解释模型为

φ=(A1ρb+B1)·q1(k)+(A2Δt+B2)·

q2(k)+(A3φN+B3)·q3(k)

(9)

表4为分类成岩储集相密度、声波时差及中子孔隙度联合求取孔隙度解释模型表。可以看出,与密度和声波时差的权系数相比,中子孔隙度的权系数较小,这是由于气藏普遍存在的挖掘效应造成的。随着成岩储集相类型的变差,中子孔隙度权系数有所升高,说明随着储层越来越致密,无效孔隙增多,孔隙度受挖掘效应的影响有变弱的趋势。

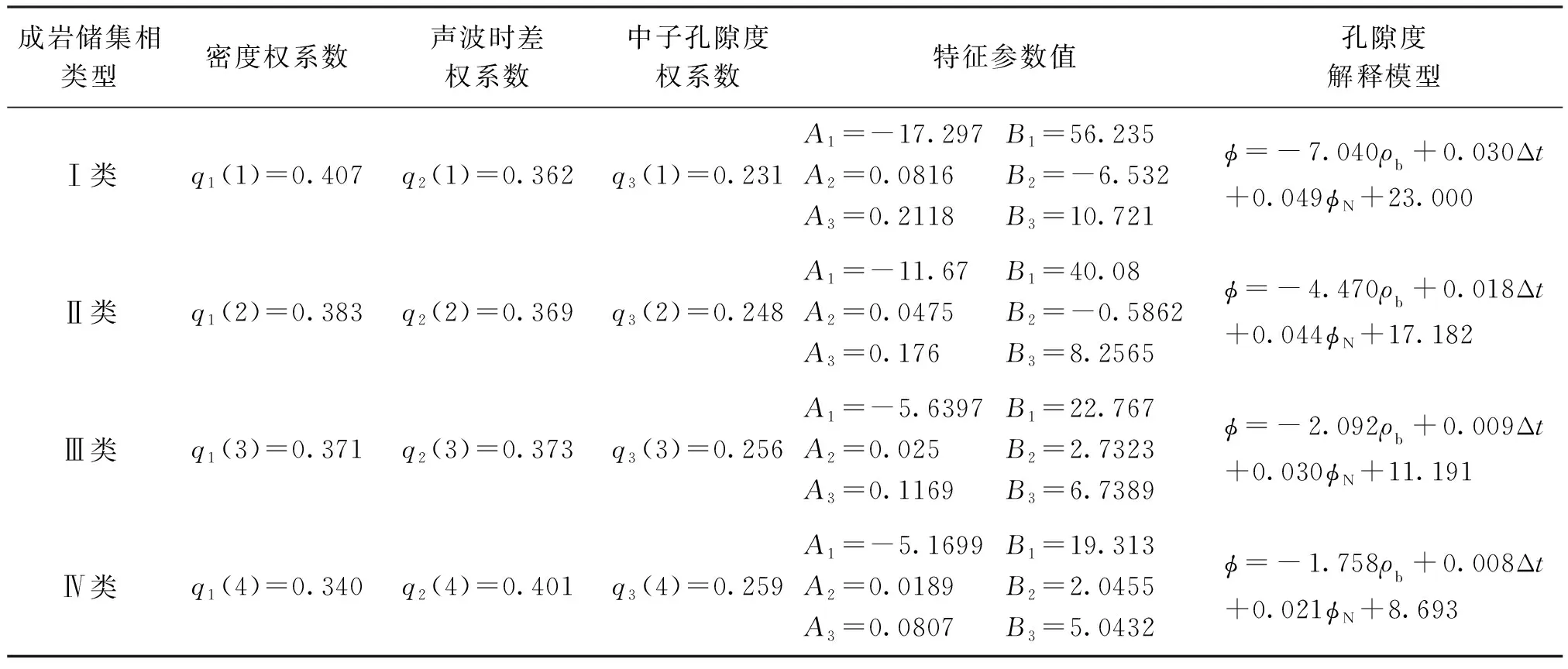
表4 致密储层分类成岩储集相密度、声波时差及中子孔隙度综合拟合计算孔隙度模型表

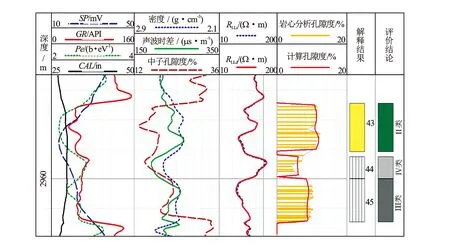
图4 Z18井盒8上段致密气储层分类成岩储集相测井综合评价解释成果图

4 检验结果实例分析

图4为研究区非建模井Z18井盒8上段分类成岩储集相测井综合评价解释成果图。图4中2 954.88～2 958.17 m井段的第43层综合评价为Ⅱ类较好型成岩储集相。根据表4中Ⅱ类成岩储集相测井解释孔隙度模型:φ=-4.470ρb+0.018Δt+0.044φN+17.182,利用密度、声波时差及中子孔隙度综合信息,将该层段密度测井值2.470 g/cm3、声波时差测井值242.319 μs/m、中子孔隙度测井值17.791%代入计算该层段平均孔隙度为11.28%,与岩心分析孔隙度11.23%相对比,相对误差0.4%。同样44、45层分别评价为Ⅳ类、Ⅲ类成岩储集相,分别利用相应分类解释模型求取孔隙度为6.07%和8.80%,其相对误差分别为3.4%和1.5%。经2 955.0～2 957.0 m井段第43号层Ⅱ类成岩储集相储层试气,日产气1.75×104m3,无水,应用效果好。而经统一模型计算,图4中43～45号层位孔隙度分别为12.65%,8.76%和9.88%。孔隙度越低,统一模型的计算结果偏差越大。

根据孔隙度模型的研究成果,将Z18井各取心小层的岩心分析孔隙度、传统测井解释孔隙度和经孔隙度解释模型的计算结果进行统计对比。结果表明孔隙度解释模型与岩心分析化验资料相比,其计算结果相对误差控制在3.75%以内,平均相对误差1.42%,解释精度远高于传统测井解释孔隙度,完全可以满足开发过程中的实际需要。

5 结 论

(1) 不同类别成岩储集相对孔隙度变化起着明显的控制作用,同类成岩储集相具有相似的孔隙结构和测井响应特征。因此,提出基于成岩储集相分类建立孔隙度模型的方法是可行的。

(2) 利用灰色理论集成综合各种测井信息,建立了成岩储集相测井多参数定量评价方法。在此基础上通过建立不同类型成岩储集相孔隙度参数模型,发现分类模型中数据点具有相对集中的分布趋势及较为明显的线性关系,在一定程度上克服了采用其他模型计算造成的低分辨力的评价误差。

(3) 在孔隙度分类模型计算的基础上,利用各分类模型的偏差度、离散度和相关度多参数联合求取孔隙度,兼顾每个评估值,较大限度地减小偏离较大测量结果的影响,也为同类型致密储层的参数建模研究提供了有效方法。

参考文献:

[1] 史彦尧, 宋新民, 郝志海, 等. 基于沉积微相-岩石相建立砾岩油藏测井参数解释模型 [J]. 吉林大学学报(地球科学版), 2010, 40(3): 707-712.

[2] 何辉, 宋新民, 蒋有伟, 等. 砂砾岩储层非均质性及其对剩余油分布的影响——以克拉玛依油田二中西区八道湾组为例 [J]. 岩性油气藏, 2012, 24(2): 117-123.

[3] 孟祥梅, 杨少春. 沉积微相约束下的测井解释模型研究 [J]. 物探化探计算技术, 2010, 32(3): 337-340.

[4] 王月莲, 宋新民. 按流动单元建立测井储集层解释模型 [J]. 石油勘探与开发, 2002, 29(3): 53-55.

[5] 石玉江, 张海涛, 侯雨庭, 等. 基于岩石物理相分类的测井储层参数精细解释建模 [J]. 测井技术, 2005, 29(4): 328-332.

[6] 牛晓燕, 李建明. 中扬子西部地区灯影组白云岩储层控制因素分析 [J]. 石油地质与工程, 2009, 23(5): 32-34.

[7] 郝乐伟, 王琪, 唐俊. 储层岩石微观孔隙结构研究方法与理论综述 [J]. 岩性油气藏, 2013, 25(5): 123-128.

[8] 王伟力, 高海仁. 鄂尔多斯盆地中东部致密砂岩储层地质特征及控制因素 [J]. 岩性油气藏, 2013, 25(6): 71-78.

[9] 付金华, 魏新善, 任军峰, 等. 鄂尔多斯盆地天然气勘探形势与发展前景 [J]. 石油学报, 2006, 27(6): 1-4.

[10] 杨华, 付金华, 魏新善. 鄂尔多斯盆地天然气成藏特征 [J]. 天然气工业, 2005, 25(4): 5-8.

[11] 丁圣, 钟思瑛, 周方喜, 等. 高邮凹陷成岩相约束下的低渗透储层物性参数测井解释模型 [J]. 石油学报, 2013, 33(6): 1012-1017.

[12] 成志刚, 宋子齐, 景成, 等. 苏里格东区致密气储层成岩储集相分类及特征 [J]. 断块油气田, 2012, 19(5): 577-582.

[13] 周游, 李治平, 景成, 等. 基于“岩石物理相-流动单元”测井响应定量评价特低渗透油藏优质储层——以延长油田东部油区长6油层组为例 [J]. 岩性油气藏, 2017, 29(1): 116-123.

[14] 宋子齐, 王瑞飞, 孙颖, 等. 基于成岩储集相定量分类模式确定特低渗透相对优质储层——以AS油田长61特低渗透储层成岩储集相定量评价为例 [J]. 沉积学报, 2011, 29(1): 88-95.

[15] 成志刚, 宋子齐, 景成, 等. 苏里格东区致密气藏成岩储集相分类及其测井响应特征研究 [J]. 测井技术, 2013, 37(2): 154-161.

[16] 刘锐娥, 李文厚, 拜文华, 等. 苏里格庙地区盒8段高渗储层成岩相研究 [J]. 西北大学学报(自然科学版), 2002, 32(6): 667-671.

[17] 景成, 蒲春生, 周游, 等. 基于成岩储集相测井响应特征定量评价致密气藏相对优质储层 [J]. 天然气地球科学, 2014, 25(5): 657-664.

[18] 周游, 李治平, 景成, 等. 基于流动单元控制的油藏宏观剩余油潜力分布 [J]. 特种油气藏, 2016, 23(6): 35-39.

[19] 宋子齐, 王建功. 储层定量评价指标和权系数研究 [J]. 测井技术, 1997, 21(5): 351-355.