非对称六相永磁同步电机的故障容错控制

刘林阴，李 杰

(郑州科技学院，郑州 450064)

非对称六相永磁同步电机的故障容错控制

刘林阴，李 杰

(郑州科技学院，郑州 450064)

摘 要：针对由非对称六相永磁同步电机(PMSM)和T型中点钳位型(T-NPC)三电平变频器构成的电力传动系统的可靠运行问题，提出了一种新型复合容错控制策略。结合简化空间矢量调制(SVM)和直接转矩控制(DTC)形成了非对称六相PMSM的SVM-DTC控制方案，并设计了谐波电流抑制单元，同时获得了较好的电流谐波性能和快速动态响应。通过解析分析开路故障下各相定子磁链与定子电压之间的关系，设计了SVM-DTC方案下的开路故障容错控制策略。通过样机实验，验证了控制方案的效果。

关键词：非对称；六相永磁同步电机；三电平变频器；故障容错控制；直接转矩控制

0 引 言

近年来，多相永磁同步电机(以下简称PMSM)驱动系统在许多工业领域得到应用，特别是大功率推进系统中，如高铁，电动汽车和船舶推进等[1-3]。多相PMSM通常对应使用T型中点钳位型(以下简称T-NPC)三电平变频器，可具有电压谐波少，共模电压小，电磁干扰小，高效，高容错能力等优点[4-5]。对于桥臂故障，两电平变频器和二极管钳位型变频器需完全弃用故障桥臂，而T-NPC变频器则不需要，因而易于容错控制；在开路故障的情况下，故障相可通过电路重构连接至三电平变频器直流中性点，结合中性点电压控制，可容错运行，而两电平变频器则难以实现平衡[6]。

对于六相PMSM，采用非对称绕组形式可以消除6次谐波[7-8]。文献[9]设计一种基于改进空间矢量调制(以下简称SVM)的磁场定向控制策略，可以消除低次谐波，但动态性能欠佳；而文献[10-11]所涉及的基于开关表的直接转矩控制(以下简称DTC)动态响应快，但谐波也较大。文献[12]将两种控制策略结合形成SVM-DTC方案，虽具有两者的优点，但局限于三相电机应用，故本文将SVM-DTC推广至六相电机。多相电机驱动系统中，开路故障较为典型，由功率器件失效或定子绕组问题引起，最为简单的解决方案是切断整个故障绕组[13]，但多相电机相数恶化将导致输出功率降低，且转矩脉动增大。文献[14]研究了五相感应电机的容错控制策略，但局限于磁场定向控制下容错。

本文的目的是构建一个高可靠性的低压大功率电力传动系统。故在前述文献研究基础上，进行了重新设计和推广，研究了一种非对称六相PMSM驱动系统的故障容错控制方案。该方案基于SVM-DTC策略，继承了SVM较好的谐波性能和DTC快速的动态性能，并能应对电机开路故障。最后，通过实验对方案进行验证。

1 六相PMSM驱动系统配置和模型

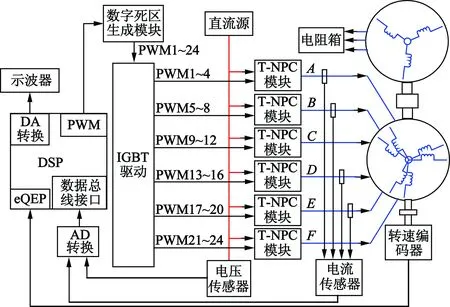
图1为非对称六相PMSM和T-NPC变频器构成的驱动系统配置。六相PMSM两套三相绕组夹角为30°。

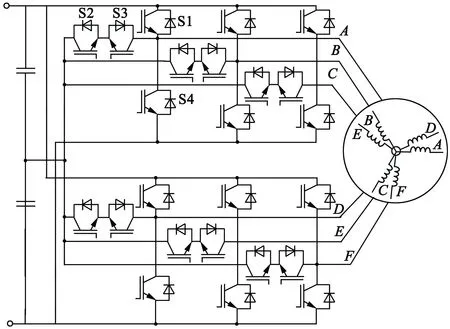
图1 非对称六相PMSM驱动系统

电机的电压和磁链方程：

(1)

式中：us为定子电压矢量;is为定子电流矢量;ψs为定子磁链矢量;ψf为转子磁链矢量;θ为d轴和A相绕组之间的相位角;p为微分算子。F(θ)具体如下：

(2)

电感矩阵Ls可表示：

Ls=LlsI6+LmsA+LmrB

(3)

式中：Lls为漏电感;I6为6维单位矩阵;Lms为定子电感;Lmr为励磁电感。矩阵A和B分别：

(4)

(5)

根据矢量空间分解方法[15]，非对称六相PMSM的电压和电流矢量可分解为3个二维正交子空间：α-β,x-y和o1-o2。下式给出了分解矩阵TVSD：

(6)

2 SVM-DTC控制策略

图2为非对称六相PMSM驱动系统的SVM-DTC控制方案框图。控制器主要包含转速闭环、转矩和磁链估计、电压矢量预测、简化SVM以及谐波电流控制。

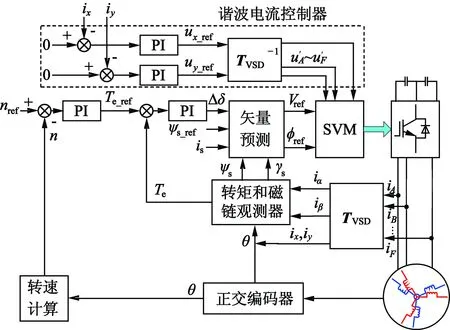
图2 SVM-DTC控制器框图

2.1 转矩和磁链估计

图3为基于电流模型的定子磁链计算流程[16]。不同于基于电压模型的定子磁链估计，基于电流模型的磁链估计受电压信号约束，当发生开路故障时，仍然可以精确计算定子磁链。电机转矩可以通过下式计算：

Te=3p(ψsαisβ-ψsβisα)

(7)

式中：Te为电磁转矩;p为极对数;ψsα和ψsβ为α,β轴定子磁链;isα和isβ为α,β轴定子电流。

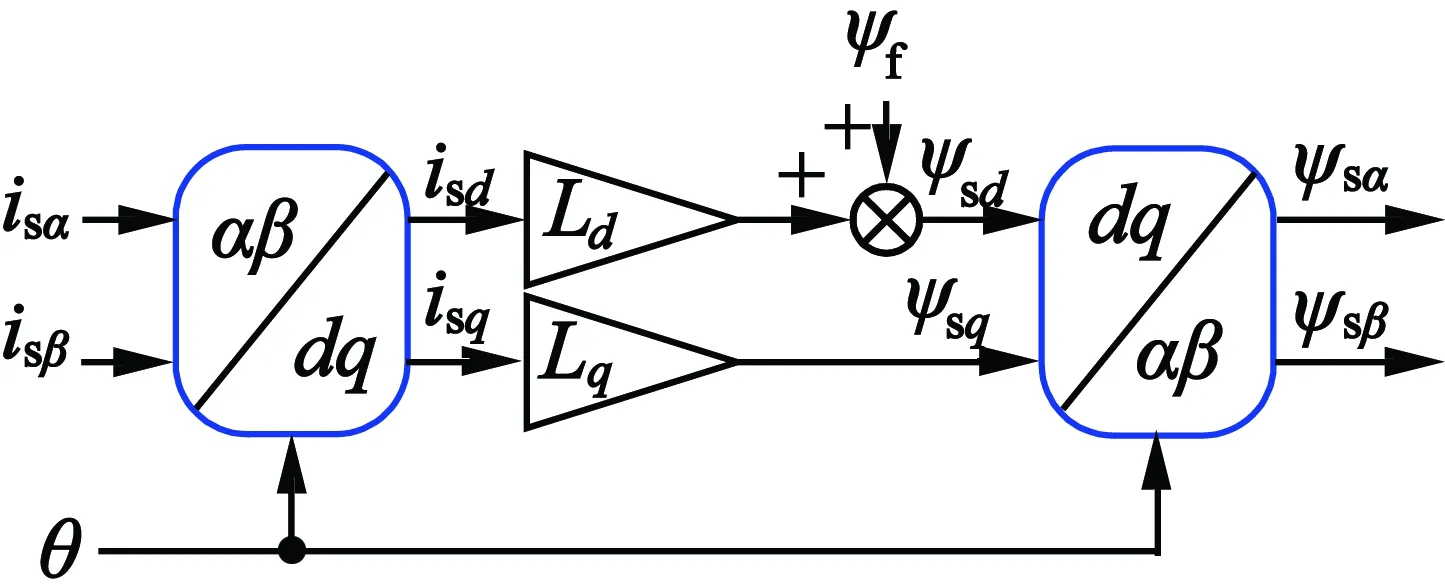
图3 基于电流模型的定子磁链计算

2.2 电压矢量预测

图4为定子磁链控制原理。图4中，γs为定子磁

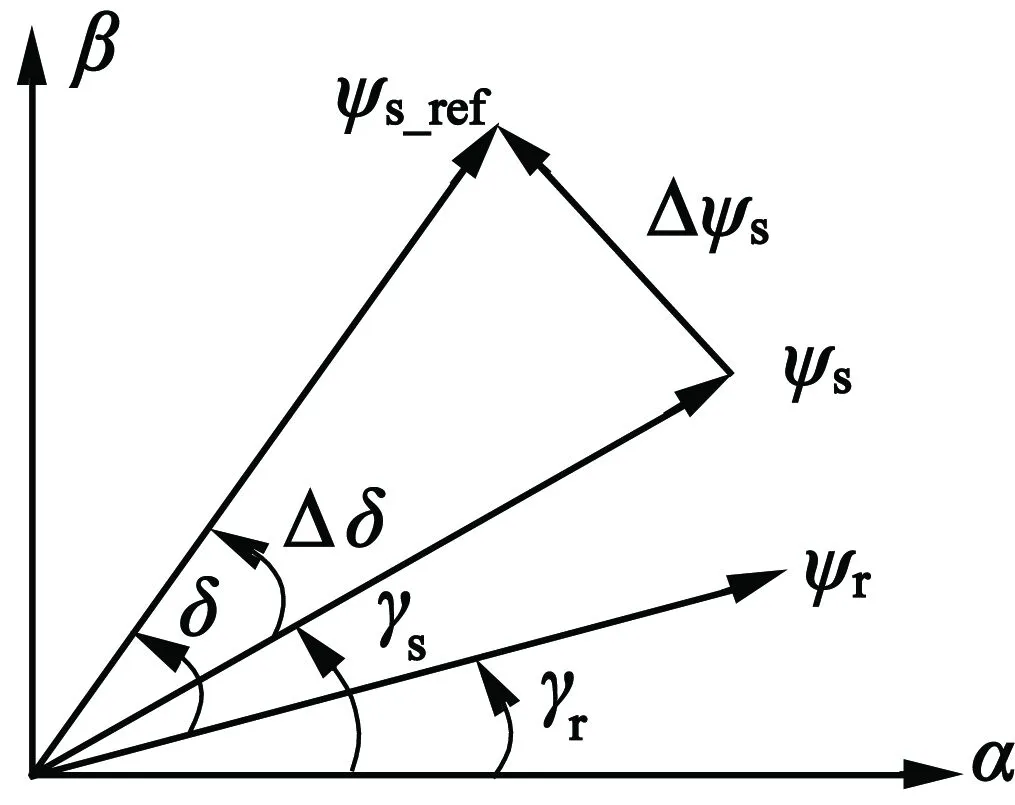
图4 定子磁链控制原理

链角，γr为转子磁链角，定子磁链矢量误差Δψs决定了定子磁链矢量参考ψs_ref与电压矢量参考Vref之间的关系：

Δψs=ψs_ref-ψs=VrefTs

(8)

式中：Ts为开关周期。

2.3 简化SVM

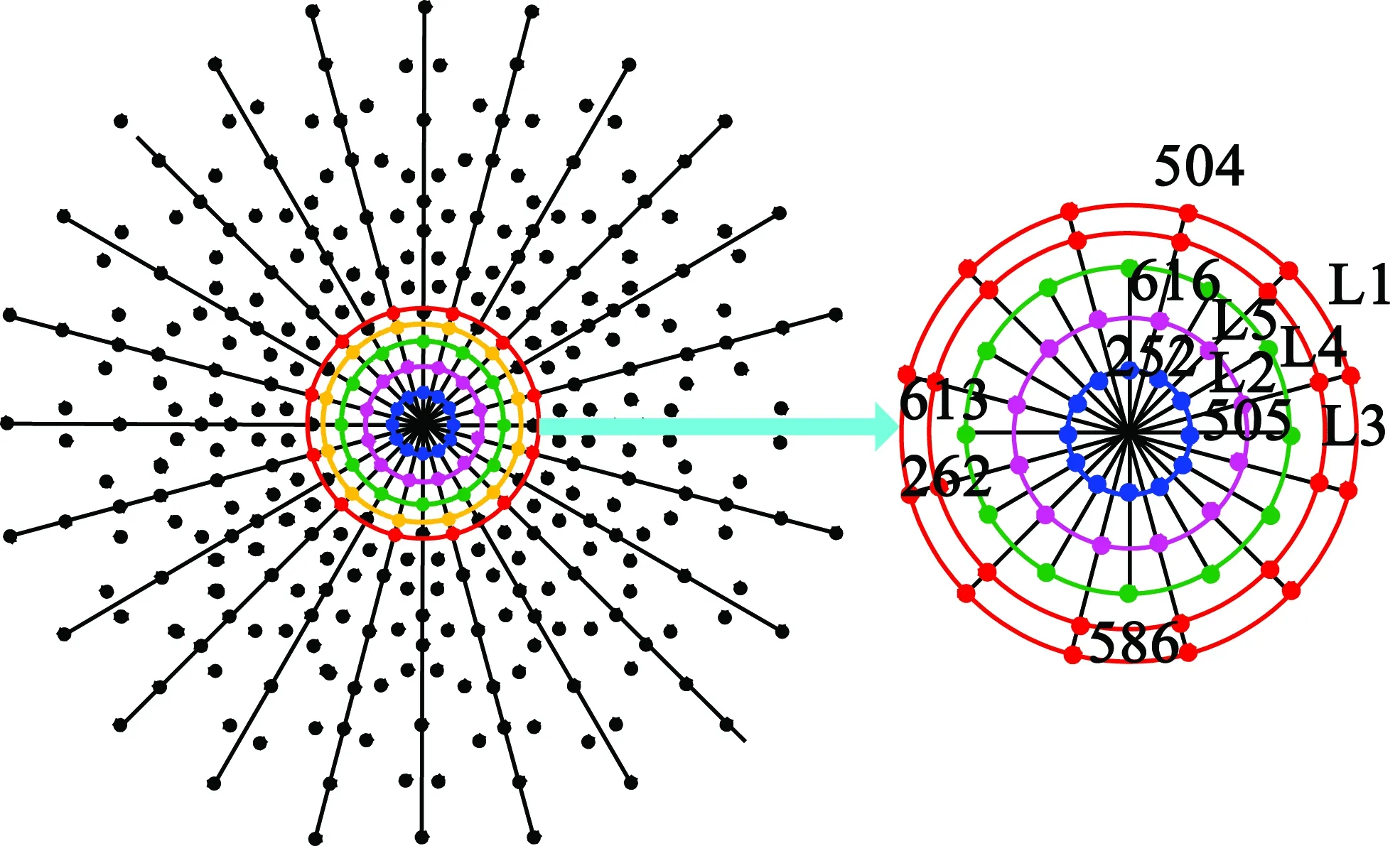
如图5所示，729个基本电压矢量映射到α-β子空间和x-y子空间，以十进制形式描述。例如，矢量210 201可表示为十进制的586。黑色点表示所选择的点，具体根据其在α-β子空间的幅值可分为5组：L1,L2,L3,L4和L5，如表1所示。

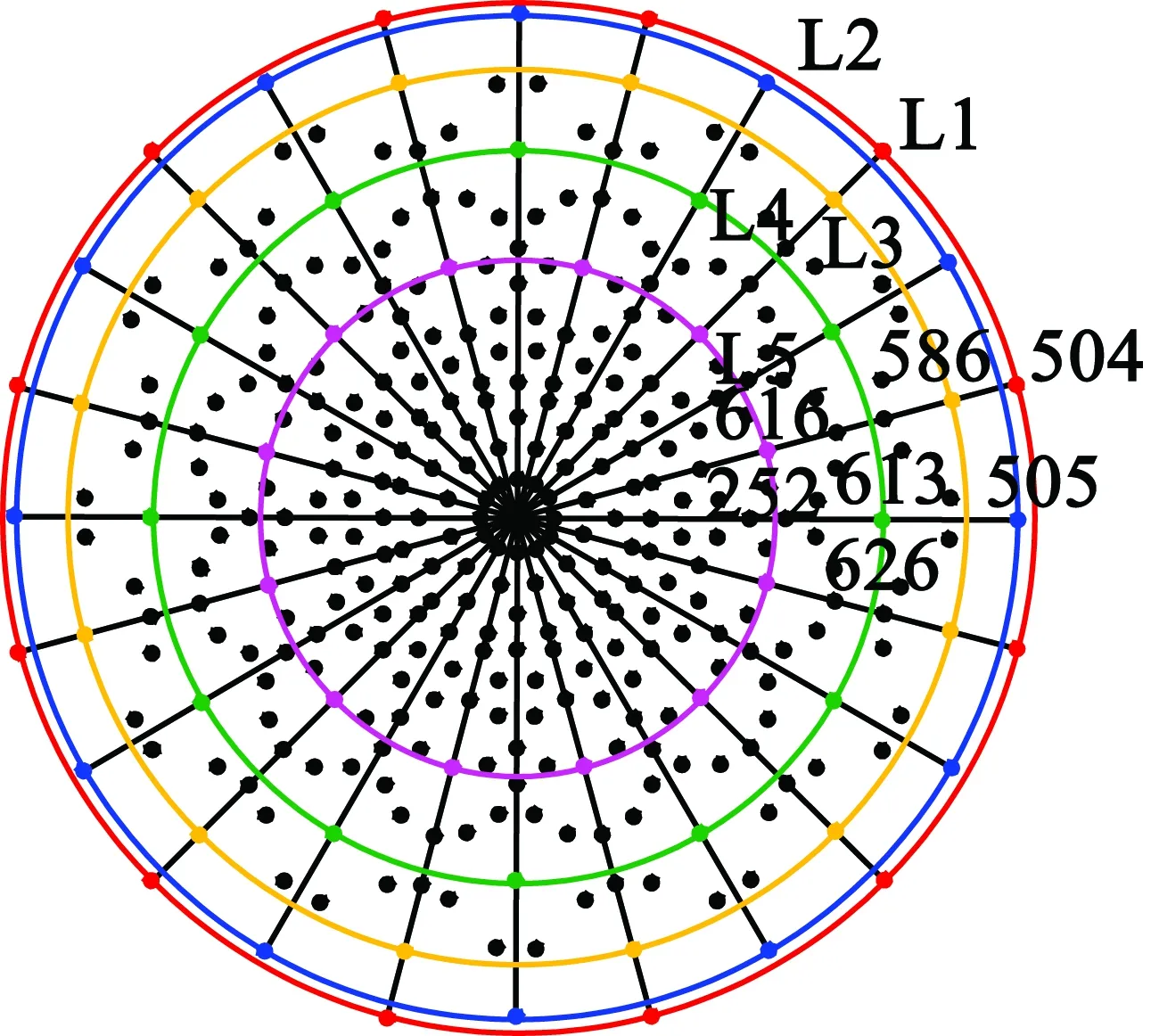
(a) α-β子空间

(b) x-y子空间

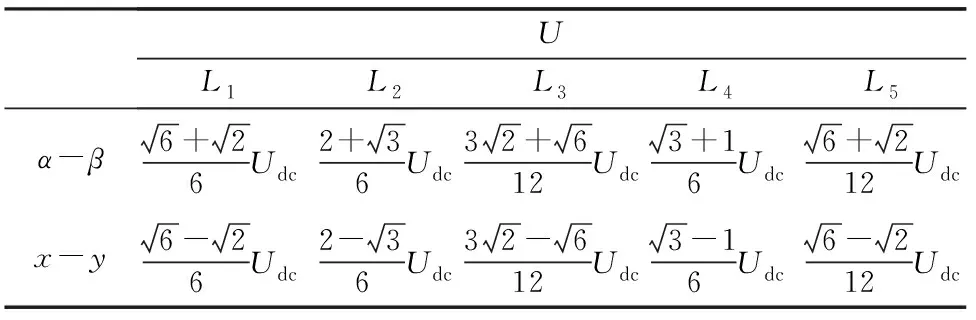
UL1L2L3L4L5α-β6+26Udc2+36Udc32+612Udc3+16Udc6+212Udcx-y6-26Udc2-36Udc32-612Udc3-16Udc6-212Udc

电压矢量合成的第一步，选择α-β子空间上相同矢量方向的L1和L3,L3和L5以及L2和L4组成3组新矢量，即L1-3,L3-5和L2-4，从而可以得到如图6所示的x-y子空间上的无谐波矢量集合。x-y子空间上依然需要约束电压矢量的平均伏秒保持为零，故可计算出如表2所示的持续时间，其中Pi-j(i)和Pi-j(j)为Li和Lj的时间权重系数，两者之和为零，而Li和Lj合成了Li-j。根据表1可计算出L1-3,L3-5和L2-4幅值，如表3所示。

图6 α-β子空间下的无谐波电压矢量

表2 选定矢量的持续时间分布

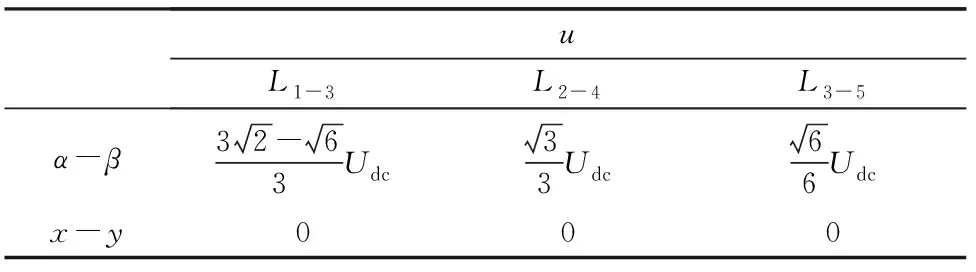
表3 新合成矢量的幅值

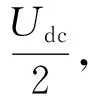
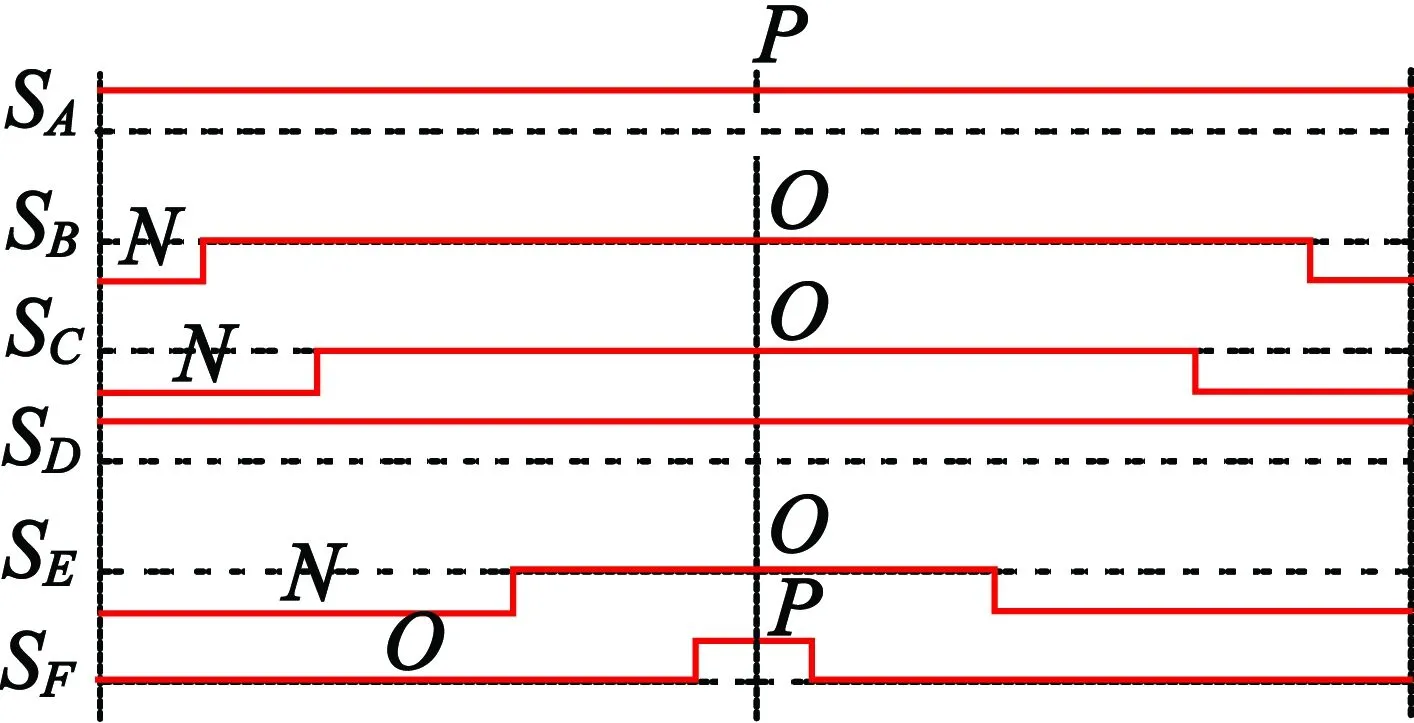
图7 开关序列

2.4 电流谐波抑制

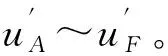
3 开路故障容错方案

为了实现系统开路故障容错控制，首先需要推导正常条件下端电压与开路故障时故障相反电动势之间的电压差,然后，该电压差将由其他非故障相进行补偿。如图8所示，设F相处于开路故障，则正常条件下F相的端电压为uF，故障绕组反电动势为uEMF,两者压差为ΔuF。

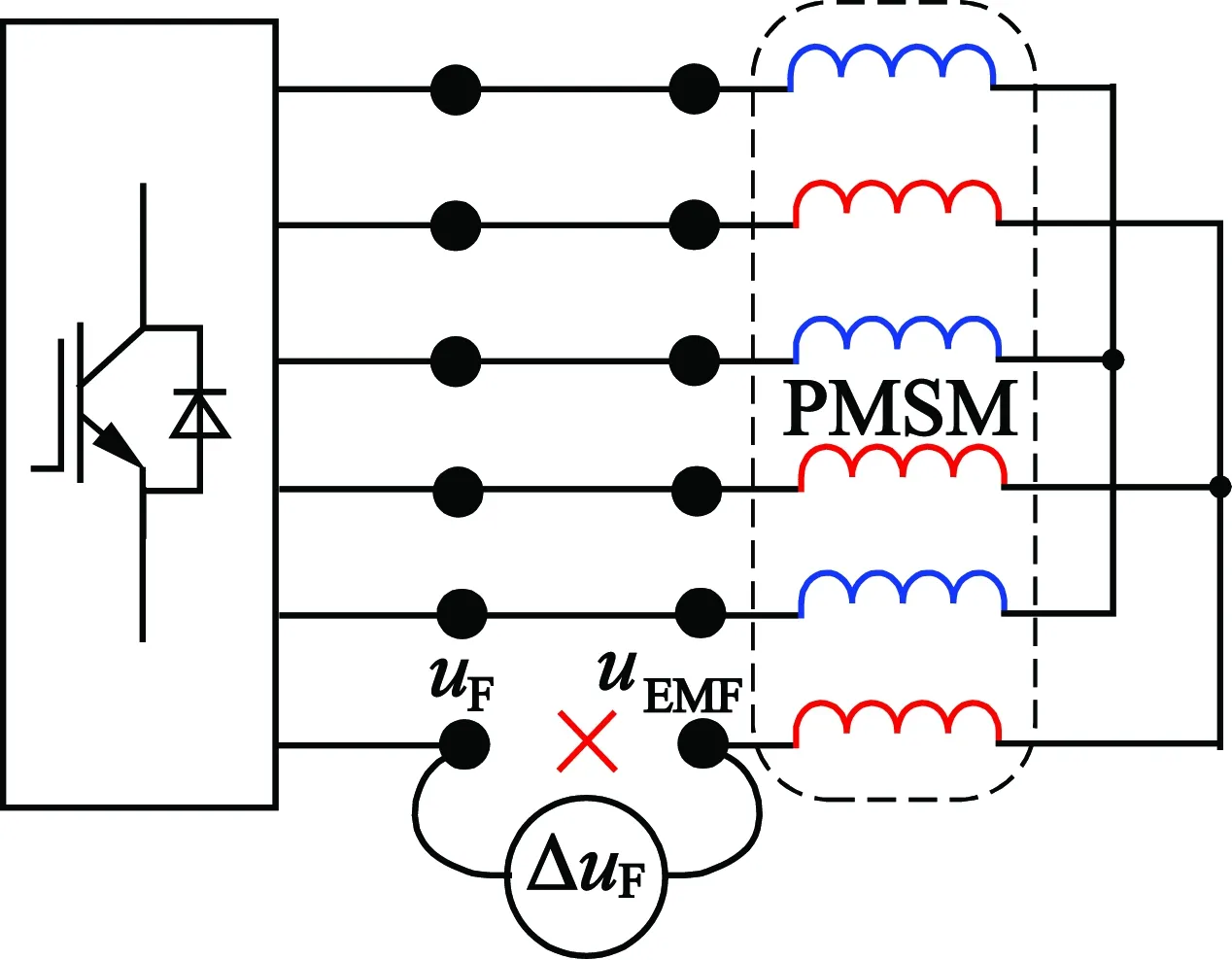
图8 F相开路故障示意图

由于非对称六相PMSM的相电压符合对称约束条件，电机相电压可由线电压表示如下：

(9)

式中：uA～uF为A相至F相的端口电压;uAB～uEF为A相至F相的线电压。在α-β和x-y子空间上的电压可由式(6)和式(9)得到：

(10)

当F相发生开路故障时，线电压uAB，uBC和uDE不变，仅uF发生改变，其值从原来正常下的端电压值变为F相的总反电动势。而且uβ和uy都将受到uF变化的影响。因此，关键是得出ΔuF的解析表达式，uF的表达式：

(11)

我国标准化工作的问题还突出反映在缺乏既具有标准化知识又具有钻井液等专业知识的综合型人才上，虽然最近几年胜利石油管理局加强了对标准制修订人员的技术培训，但是力度还不够。

ψD+ψE=Lls(iD+iE)+

ψmrD+ψmrE

(12)

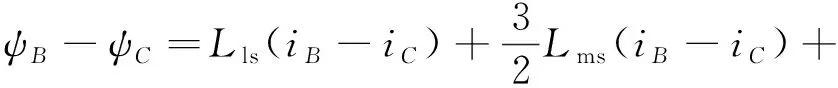
(ψmrB-ψmrC)

(13)

式中：ψmrB，ψmrC，ψmrD和ψmrE为B相,C相,D相和E相的励磁磁链，有ψmr=LmrBis=[ψmrAψmrBψmrCψmrDψmrEψmrF]T。

考虑到iA+iB+iC=0，iD+iE=0和iF=0，式(12)可改写：

ψmrD+ψmrE

(14)

从而，基于式(13)和式(14)进一步推导可得：

(ψmrB-ψmrC)

(15)

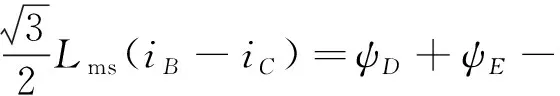
(ψmrD+ψmrE)

(16)

联立式(15)和式(16)，可得：

(17)

将式(17)代入式(11)，得到故障相电压：

(18)

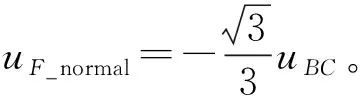
(19)

基于式(10)和式(19)，故障后α-β子空间的定子电压调整：

(20)

为了在开路故障下获取相同的电压矢量输出效应，参考电压uref_α不需要改变，而uref_β应加上Δuβ。由于故障导致谐波子空间发生变化，控制维度从6个维度减少到5个维度，故需通过构造新的5维正交矢量矩阵来导出谐波矢量。将F相从式(6)中移除后有：

(21)

可以计算出对应于α-β子空间和o1-o2子空间的4个矢量彼此正交。剩余的一维谐波矢量z与其他4个矢量正交，即：

(22)

综上，得到了F相开路故障的最终变换矩阵，而图2的容错控制框图中的矩阵需要修改。将式(5)变为新的5维正交矩阵，可推导谐波电压uz：

(23)

对比式(6)和式(23)，可注意到电压ux和uz在F相开路故障下也具有相同的表达式。为了简化，谐波维数仍由x表示，而y维分量忽略。同时，基于式(9)～式(24)的开路故障容错方案可以适用于任意相，而在两相开路故障的情况下，故障相的电压仍然可以通过其他正常相来进行补偿。

4 实验验证

为了验证前述设计控制方案，基于如图9所示

(a) 实验系统图

(b) 实验系统照片

实验平台进行了相关实验研究。实验装置主要包括由6个T-NPC模块构建的变频器，非对称六相PMSM，两者构成驱动系统对拖永磁同步发电机及其电阻负载箱。实验中采用DSP(TMSF28335)执行控制算法，并生成12通道PWM信号，然后添加死区后完成24通道互补PWM信号到IGBT驱动器。实验系统主要参数如表4所示。实验中的电压电流量采用霍尔传感器采集，转速通过转速编码器获取。开路故障采用禁止特定IGBT信号来模拟实现。

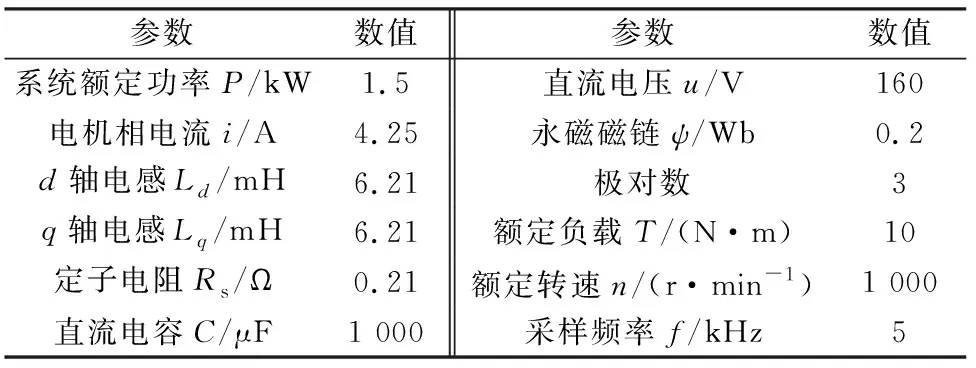
表4 主要实验参数

图10为采用新型SVM-DTC控制策略的系统稳态输出波形。电机转速为1 000 r/min，负载转矩为10 N·m，其中图10(a)为变频器输出相电压波形，图10(b)为电机定子电流波形，图10(c)为谐波电流分量，图10(d)为定子磁链轨迹。从图10中可以看出，电流低频谐波被有效地抑制，磁链轨迹稳定。

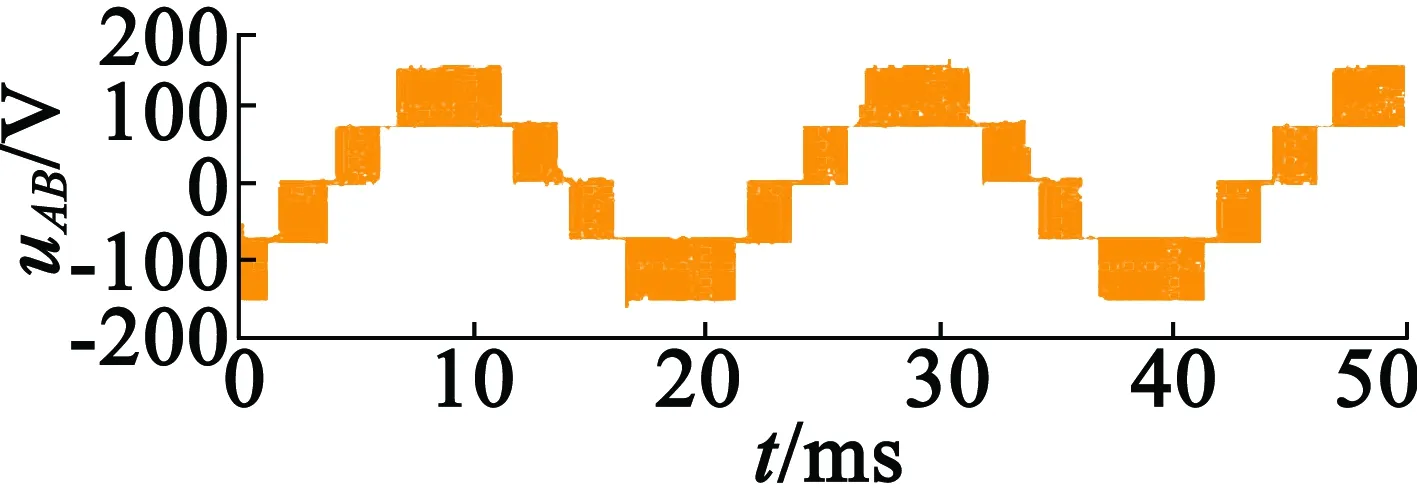
(a) 输出相电压

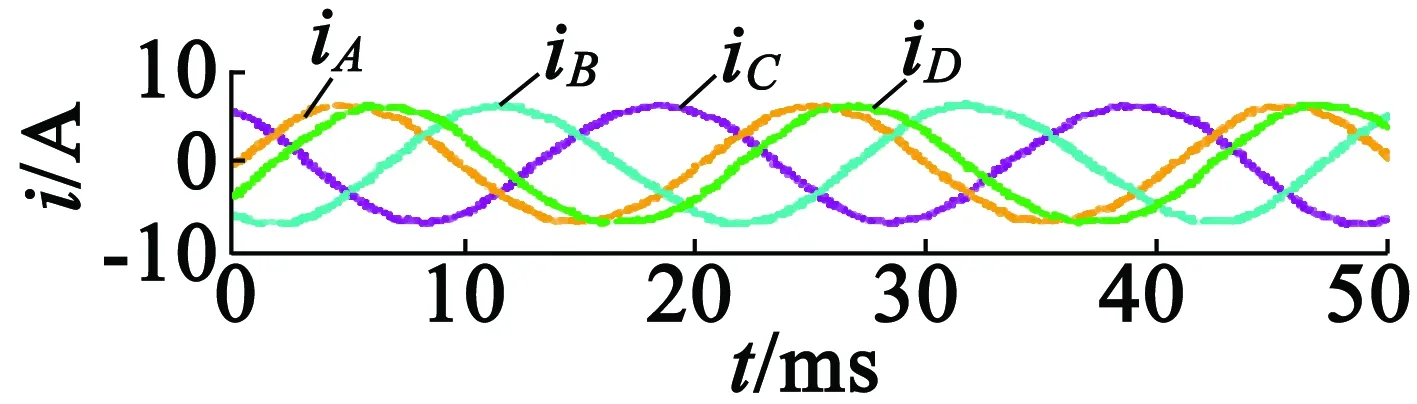
(b) 定子电流

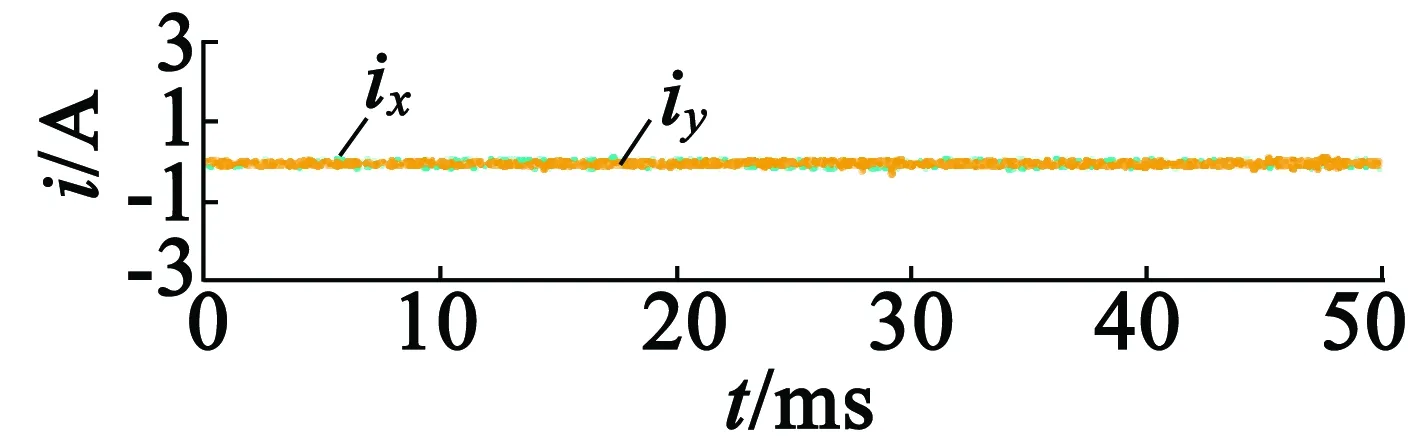
(c) 谐波电流分量

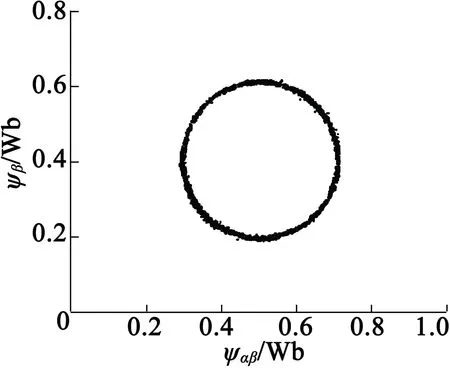
(d) 定子磁链轨迹

图11为不使用容错控制时，F相开路故障后的实验结果。其中故障时间点t=50 ms，图11(a)为电机输出转矩波形，图11(b)和图11(c)为电机定子电流波形。从图11中可以看出，故障发生后，出现了较大的转矩波动，F相的电流为零。

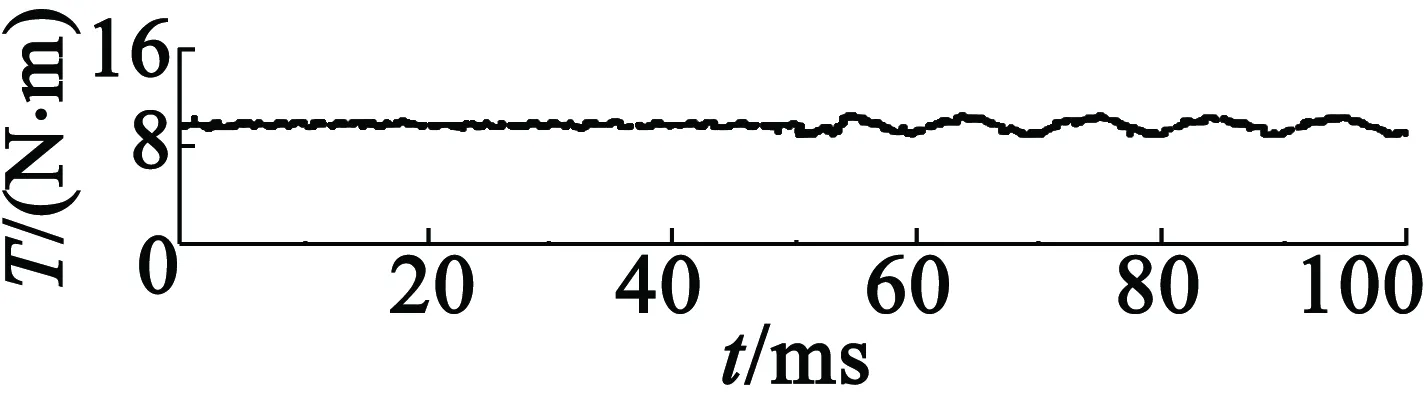
(a) 输出转矩

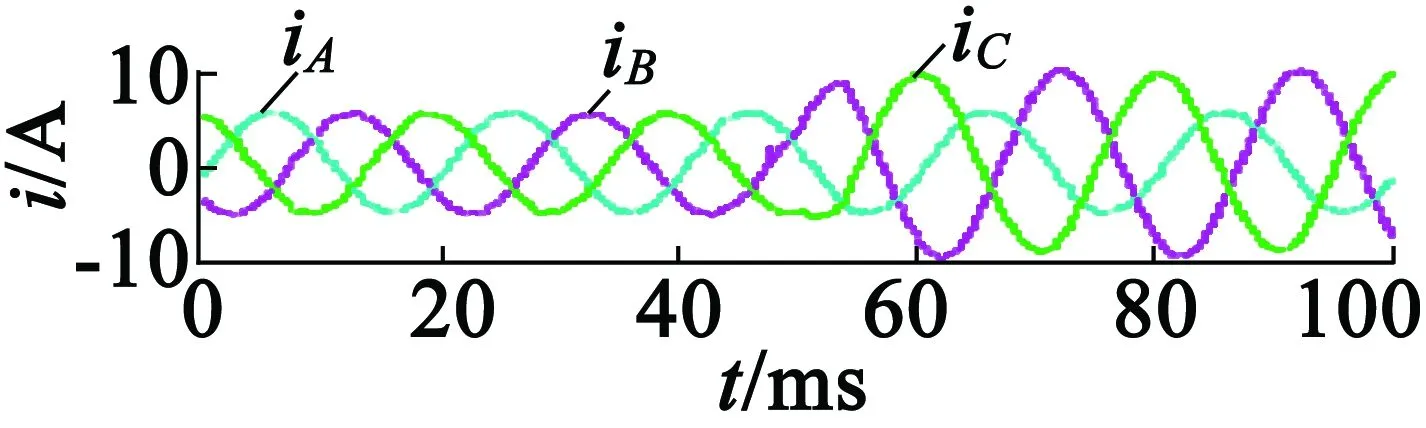
(b) A，B和C相定子电流

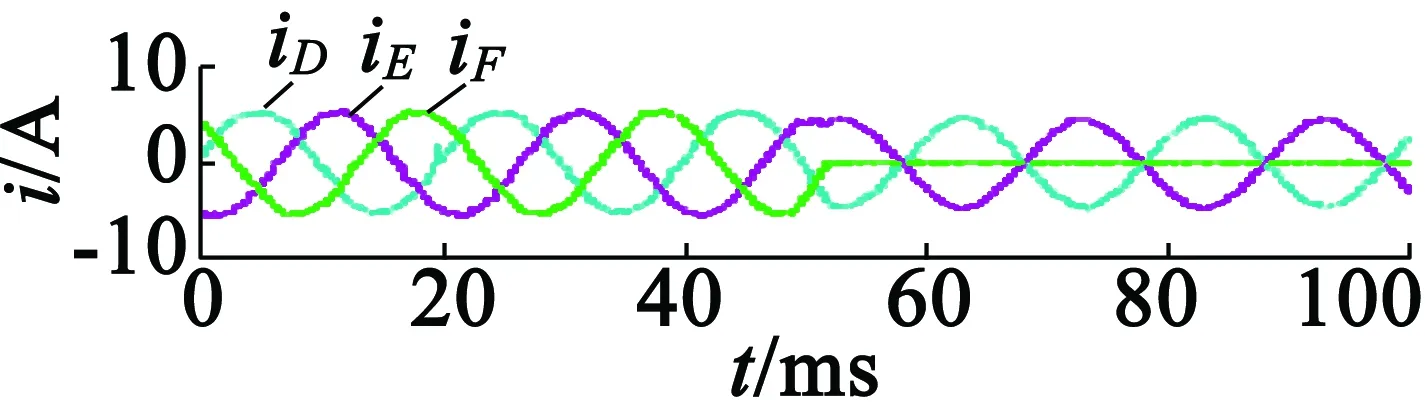
(c) D,E和F相定子电流

图12为F相开路故障后，实施容错控制时的实验结果。具体在t=150 ms后施加了故障容错控制，其中图12(a)为电机输出转矩波形，图12(b)和图12(c)为电机定子电流波形，图12(d)为β轴电压参考和β轴电压参考补偿波形。结合图12(b)和图12(c)可看出，电压补偿施加后获取了更低的电流谐波。从图12中可以看出，故障发生后，由于施加了容错控制，原来较大的转矩波动得到了抑制，趋于平稳，实验结果验证了容错控制的有效性。

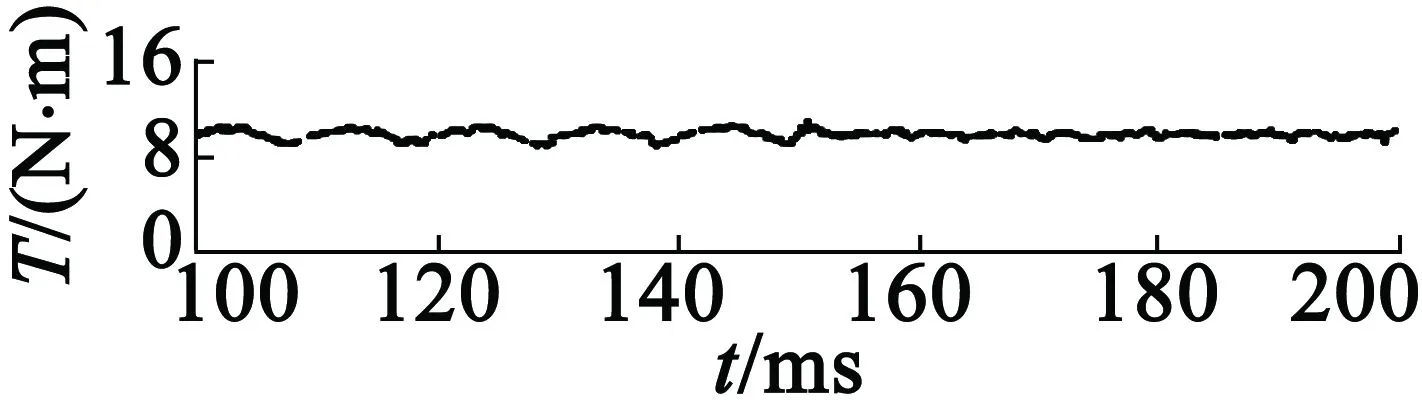
(a) 输出转矩

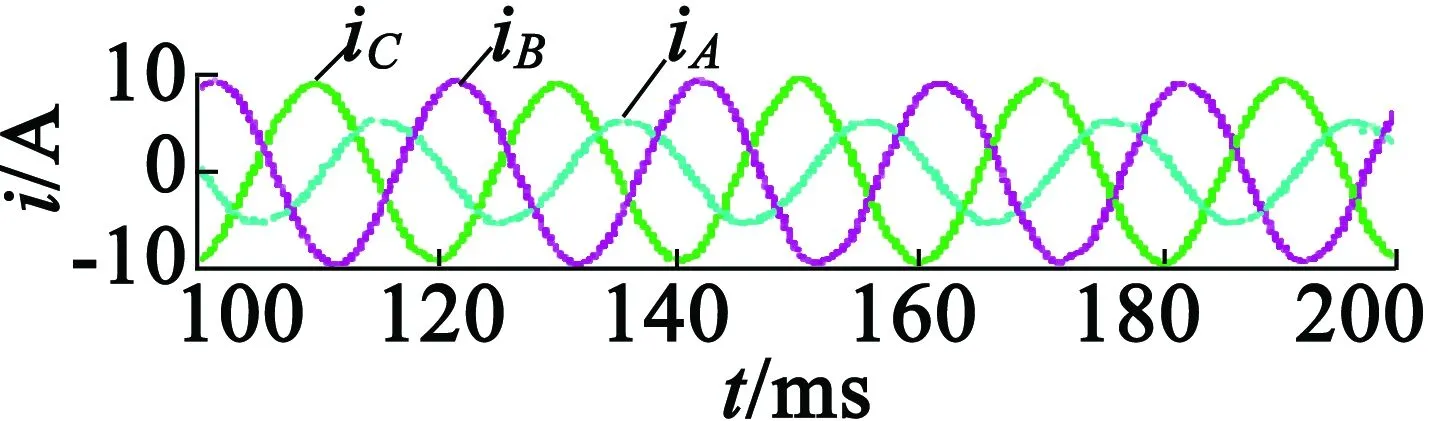
(b) A,B和C相定子电流

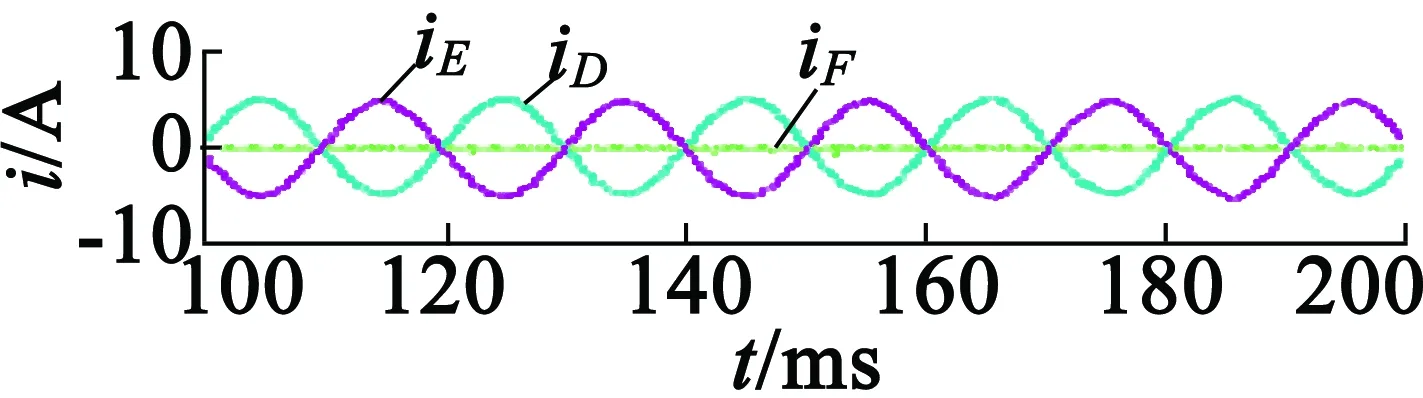
(c) D,E和F相定子电流

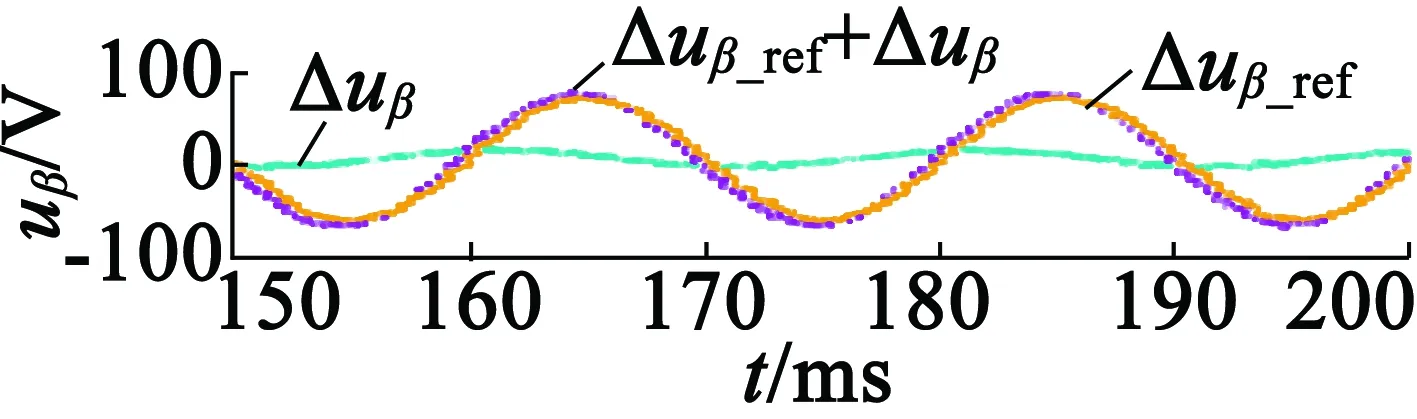
(d) β轴电压参考和电压参考补偿

5 结 语

本文围绕非对称六相永磁同步电机驱动系统可靠运行，研究了一种新型开路故障容错运行策略。现总结主要结论：

1) 在设计简化SVM中利用了x-y子空间上的无谐波矢量集合，有效优化电压矢量合成，并结合谐波电流控制器实施后降低了电机电流谐波，从而降低了转矩波动，并经由实验结果进行了验证，同时控制器无需改变DTC的控制结构；

2) 开路故障容错的关键是导出定子磁链与故障后所有相定子电压之间的关系，再推导出电压扰动后并将其加到电压参考上。进一步研究方向是分析T-NPC逆变器不同位置IGBT故障时的完整容错方案。

[1] 郑萍，雷雨，吴帆，等．电动汽车用六相永磁容错电机的分析和设计[J]．电机与控制学报，2013，17(6)：29-36．

[2] 史贤俊，刘陵顺，王昉．零序谐波驱动六相PMSM双电机串联系统研究[J]．电气传动，2013，43(1)：8-11．

[3] 郭新华，陈银，尚荣艳，等．不同绕组型式双移30°六相永磁同步电机建模与谐波电流优化控制[J].电工技术学报，2016，31(2)：56-63．

[4] 张旭隆，王峰，纪雯，等．基于虚拟磁链矢量的T-NPC逆变器SVPWM控制[J]．电力电子技术，2016，50(7)：12-13．

[5] 姚修远，吴学智，杜宇鹏，等．T型中点钳位三电平逆变器的零电流转换软开关技术[J].电工技术学报，2016，31(23)：179-188．

[6] WANG Z,ZHANG B,WANG Y,et al.Analysis and control of active neutral-point-clamping three-level inverters under fault tolerant operation modes[C]//International Conference on Electrical Machines and Systems.IEEE,2016:2140-2146.

[7] 周扬忠，程明，熊先云．具有零序电流自矫正的六相永磁同步电机直接转矩控制[J].中国电机工程学报，2015，35(10)：2504-2512．

[8] 史友情，陶彩霞．六相永磁同步电机谐波电流抑制技术[J]．电机与控制应用，2017，44(3)：90-95．

[9] HADIOUCHE D,BAGHLI L,REZZOUG A.Space vector PWM techniques for dual three-phase AC machine: analysis,performance evaluation and DSP implementation[J].IEEE Transactions on Industry Applications,2006,42(4):1112-1122.

[10] 秦英，朱熀秋，张丽，等．永磁同步电机直接转矩控制新型建模方法[J]．微特电机，2015，43(7)：89-91．

[11] 孙旭霞，高沁源，孙伟．基于SVPWM的永磁同步电机直接转矩控制系统[J]．电气传动，2016，46(11)：3-6．

[12] 李君，李毓洲．无速度传感器永磁同步电机的SVM-DTC控制[J]. 中国电机工程学报，2007，27(3)：28-34．

[13] 宝金，巩瑞春，李强，等．基于直接转矩控制的永磁容错电机故障补救策略研究[J]．微特电机，2016，44(9)：92-96．

[14] 康敏，孔武斌，黄进．电动汽车用五相感应电机容错控制[J]．电机与控制学报，2014，18(3)：1-6．

[15] ZHAO Y,LIPO T A.Space vector PWM control of dual three-phase induction machine using vector space decomposition[J].IEEE Transactions on Industry Applications,1994,31(5):1100-1109.

[16] 金孟加，邱建琪，史涔溦，等．基于新型定子磁链观测器的直接转矩控制[J].中国电机工程学报，2005，25(24)：139-143．

FaultTolerantControlofAsymmetricSix-PhasePermanentMagnetSynchronousMotor

LIULin-yin,LIJie

(Zhengzhou College of Science & Technology,Zhengzhou 450064,China)

Abstract:Aiming at the reliable operation problem of power transmission system composed of asymmetric six-phase permanent magnet synchronous motor (PMSM) and T-type neutral-point-clamping (T-NPC) three-level inverter, a new composite fault-tolerant control strategy was proposed. SVM-DTC control scheme of asymmetric six-phase PMSM was formed by combining simplified space vector modulation (SVM) and direct torque control (DTC), and a harmonic current suppression unit was designed at the same time, so better current harmonic performance and fast dynamic response are obtained. Based on the analysis of the relationship between the stator flux and the stator voltage in the open-circuit fault, the open-circuit fault-tolerant control method under the SVM-DTC scheme was obtained. The effect of the new control scheme is verified by PMSM drive system prototype tests.

Key words：asymmetrical; six-phase permanent magnet synchronous motor; three-level inverter; fault-tolerant control; direct torque control (DTC)

中图分类号：TM351

A

1004-7018(2018)05-0052-06

2017-07-06

河南省科技厅科技攻关项目(172102210114)

作者简介：刘林阴(1985—)，女，讲师，硕士，主要研究方向为电力电子与电力传动，以及控制理论工程。