基于精英保留策略与爆炸算子的改进遗传算法
罗凤鸣,吕方林,侯宗琰
(东北石油大学电气信息工程学院, 黑龙江 大庆 163318)
遗传算法[1]是一种模拟物种进化的智能算法。它在寻优过程中不需要复杂的微分和积分公式,只须生成大量的随机数在解空间中进行搜索,即可得到较为合理的最优解,因此,受到学者的广泛关注。遗传算法具有较强的优化性和鲁棒性,已经在参数调节、路径规划等领域[2-5]得到了应用;但是随着问题维数的提高和约束条件的增多,标准遗传算法已经无法精确地处理该类问题,寻优过程中存在着收敛缓慢、易早熟和精度低等缺陷[6-7],难以获得正确的全局最优解。
针对标准遗传算法存在的缺陷,研究者提出了很多改进措施[8-13]。陈碧云等[8]提出一种多种群改进遗传算法(poly-population genetic algorithm,PPGA)以求解电力系统多目标优化问题。由于遗传算法收敛性能受变异和交叉概率的影响较大,因此,文献[8]选取不同组的变异和交叉概率进行多种群并行优化;但是由于交叉与变异概率可以形成无数对的组合,以及多种群并行进化势必会增加算法的计算复杂度的缘故,此方法仍无法根本解决问题。杜卓明等[9]在陈碧云等的基础上提出一种基于差分的自适应参数改进遗传算法(differential genetic algorithm,DGA),算法中的交叉和变异概率根据适应值做动态调整,并与差分进化算法结合,有效地解决了控制参数选取的问题;但是由于种群多样性不足,因此仍容易陷入局部收敛。针对标准遗传算法在求解非凸函数时易早熟的不足,程林辉等[10]提出一种基于免疫因子改进遗传算法(immune genetic algorithm,IGA)的混合优化算法,利用免疫算法的抗体浓度抑制原则和免疫记忆库,并通过变异算子降低种群内相似个体的数目,避免算法陷入局部收敛,但是在进化后期会出现停止现象导致收敛缓慢。S.M.H. NABAVI等[11]提出一种改进编码方式的遗传算法(improved genetic algorithm,IGA),使染色体数值精度有所提高,改进编码方式可以避免染色体之间出现“断崖式”跃变,然而,仅起到提高求解精度的作用。K. SHI等[12]提出一种基于最小生成树的改进遗传算法(minimum spanning tree genetic algorithm,MSTGA),通过聚类算法将单种群划分为多种群并行搜索计算,但是分类数目的不同对聚类算法分类效果影响较大。由于分类数目的选择是人为设定的,具有主观性,因此算法的精度不高。瞿颜等[13]提出一种带有引向因子和反向搜索技术的遗传算法(gravitational search genetic algorithm,GSGA),将引向因子融入交叉算子,以加强群体之间的信息共享,但是仍然存在着种群多样性不足的缺点。
大多数研究都围绕交叉和变异运算等控制参数的改进,鲜有在生物进化原理上进行改进。为此,本文提出一种具有爆炸算子的改进遗传算法(FGA),引入爆炸算子在原种群基础上产生新种群,将多个种群结合起来搜索以提高种群的多样性和竞争能力,最后采用精英保留策略以保留搜索过程中的最优个体。
1 FGA算法
1.1 FGA算法
标准遗传算法(SGA)是一种模拟生物界“优胜劣汰”策略的启发式进化算法,是广泛应用于各领域数值寻优的智能算法之一;但是依然存在易陷入局部最优值、全局搜索能力差、鲁棒性不强等缺陷。FGA算法是在SGA算法的基础上引入爆炸算子和精英保留策略,其算法的基本运算步骤包括种群初始化,适应度值计算,选择、交叉和变异运算,爆炸运算,精英保留策略。
1.1.1 种群初始化
初始化通常以均匀分布概率密度函数随机生成种群。计算公式为
(1)
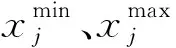
1.1.2 适应度函数
适应度函数是算法的关键,通过适应度函数对繁衍出来的后代进行量化评估,进而选择优秀个体保留至下一代。选取不同适应度函数会影响算法的收敛速度、结果和性能。常用的适应度函数有3种:绝对误差、相对误差和条件判断的适应度函数。由于本文测试函数求取的是最小值,故选用相对误差的适应度函数,计算公式为
fitness=ymax-obj。
(2)
式中:fitness表示所有解集的适应度值;obj表示所有解集的目标函数值;ymax表示解集中目标函数的最大值。
1.1.3 选择算子
本文采用的选择操作是赌转轮盘法[13],这种方法简单有效。
1.1.4 交叉算子
在交叉运算中,决定个体是否进行运算的参数是交叉概率(Pc),其范围设置为0.6~0.9。计算公式为:
(3)
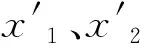
1.1.5 变异算子
同交叉运算类似,决定个体变异的参数是变异概率(Pm),变异概率范围设置为0.02~0.2。计算公式为
x(i,j)=x(i,j)+Δx。
(4)
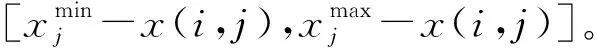
1.1.6 爆炸算子
交叉运算容易导致解集发生跃变。虽然变异运算可以进行局部搜索,但是变异概率较小,导致变异运算执行次数少。又鉴于解集发生变异多为有害的情况,故不能大幅度提高变异概率。当求解非凸函数时,算法的全局搜索能力较差。为此,谭营教授团队提出FA算子以解决全局复合函数最优化的问题[14]。该算子表示一种爆炸搜索进程,从搜索算法的角度看,要想提高算法搜索性能必须在最优解局部进行爆炸搜索,并且爆炸产生的个体数目要多,反之,距离最优解较远的则产生较少个体进行搜索。由于单个解爆炸能产生多个新个体,待爆炸的解选取过多势必会增加计算量,降低算法优化效率。基于上述分析,本文从解集中选取n(n≤10)个解进行爆炸搜索,最后结合上一代解集形成“父子混合解集”进行选择,这有效地提高了算法探索新的解空间的能力。解xi产生爆炸个体数目的计算步骤如下。
step 1,根据种群中个体优劣的不同,通过式(5)生成相应的子群。
(5)
式中:Ci表示第i个解产生的个体数目大小;μ是控制n个解产生个体总数的常量参数;ymax是解集中目标函数的最大值;ε表示最小值常量,用来避免除0错误。
step 2,为避免爆炸生成个体数目过多或过少影响算法的效率和搜索能力,需要对其进行修正。修正函数定义为:
(6)
其中,a和b是固定常量参数。
(7)
式中:Ai表示第i个解爆炸的位移幅度;Amax表示最大爆炸振幅;ymin是解集中目标函数的最小值。
h=Ai·rand(-1,1)
(8)
式中:h表示爆炸的位移距离;rand(-1,1)是区间[-1,1]上的一个随机数。
x′(i,j)=h+x(i,j),
(9)
式中x′(i,j)表示爆炸产生的新个体。若产生的新个体不满足解域空间范围,根据式(9)将其映射回解域
(10)
式中x″(i,j)为转化后满足解域范围的新个体。
1.1.7 精英保留策略
为避免交叉、变异和爆炸运算丢失和破坏上一代种群中的精英个体,故采取精英保留策略存储运算过程中的精英个体。精英保留策略[15]的核心思想是把种群进化过程中出现的精英个体复制到下一代中。精英个体是种群进化中搜索到的最优适应度值的个体,它包含目前最好的基因数据。精英保留策略有效地提高了算法的收敛能力。
1.2 FGA算法伪代码与流程图
本文采用伪代码和流程图2种形式描述FGA算法对测试函数的求解流程。FGA算法主程序伪代码如下。
Procedures of the proposed FGA algorithm
Begin
t= 0;
InitializeP(t);
P(t)={X1(t),X2(t),…,Xn(t)}
EvaluateP(t);
f(P(t))={f(X1(t)),f(X2(t)),…,f(Xn(t))}
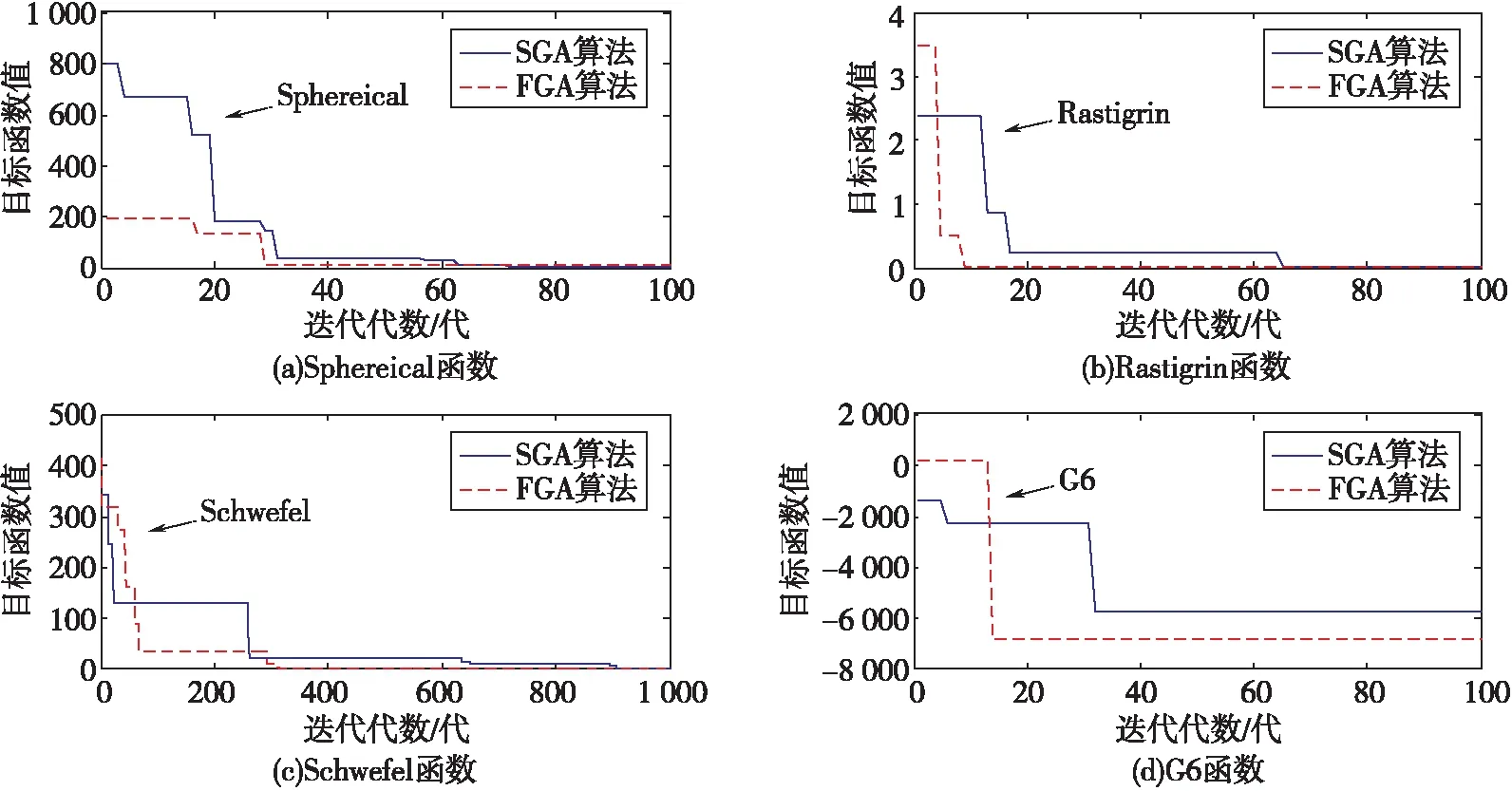
While (t Ps(t)=Selection{P(t)}; Pc(t)=Crossover{Ps(t)}; Pm(t)=Mutation {Pc(t)}; Pf(t)=Fire{Pm(t)}; EvaluatePf(t); Ift<1 then doX=min{Pf(t)}; Else IfX doX=min{pf(t)}; End End t=t+ 1; End PrintfX; End 伪代码呈现了FGA算法的主程序流程,其中t代表算法的迭代次数,tmax表示算法的最大迭代次数;InitializeP(t)表示初始化种群;P(t)表示第t代种群,Xi(t)表示第t代种群中的第i个个体;EvaluateP(t)表示评价种群,其中f(Xi(t))表示第i个个体的适应度值;Selection{P(t)}为遗传算法的选择运算,Ps(t)表示通过比较适应度值而被选中的解集;同理Crossover、Mutation 和Fire分别是交叉、变异和爆炸运算,与之对应的Pc(t)、Pm(t)和Pf(t)分别是经过交叉、变异和爆炸运算产生的新种群;X表示整个进化过程中保留的最优解。 FGA算法的具体步骤如图1所示。 图1 FGA算法流程图 step 1,随机初始化种群和迭代次数t,生成规模大小为N的初代种群Pt。 step 2,判断迭代次数t是否达到最大迭代次数tmax,若没有执行step 3,否则执行step 8。 step 3,计算解集的适应度值,使用赌转轮盘法进行选择操作,复制出N个优秀个体,形成子代种群Qt。 step 4,进行交叉、变异操作对种群进行进化(此时种群仍称为Qt)。 step 5,选取n(n≤10)个局部最优解进行爆炸运算(此时种群仍称为Qt)。 step 6,将Pt和Qt结合形成混合种群Rt,并执行精英保留策略。 step 7,从混合种群Rt生成规模为N的新种群Pt,此时t=t+1,并执行step 2。 step 8,直接输出计算结果,结束。 本文参考文献[13]中应用的测试函数,任选4个函数作为验证案例,各项参数如表1所示。利用本文提出的FGA算法和SGA算法对表1中的4个测试函数进行数值寻优。 遗传算法的参数设置为:种群大小50;测试函数Spherical、Rastigrin和G6最大迭代数为100,由于Schwefel函数较为复杂,因此求解该函数时迭代数设定为1 000;Pc取0.7,Pm取0.1;n=5,m=50,a=0.04,b=0.8,Ai=40。2种算法独立优化20次,计算测试函数所得最优解的平均值、标准差和最优值如表2所示。 表1 各项参数表 表2 规划结果 针对4个测试函数分别采用SGA算法和FGA算法进行求解,其结果如图2所示。可知,引入爆炸算子改进遗传算法后,FGA算法的收敛速度相比于SGA算法更快,搜索得到的最优解精确度更高,FGA算法的种群多样性和全局搜索能力得到了改善。 图2 2种算法收敛曲线 结合表2和图2,可得出以下结论。 1)采用2种算法对无约束的单峰函数Spherical求解。由表2可知,2种算法都可以得到理想值,但是SGA算法求得的解集平均值和标准差值明显劣于FGA算法所得的结果。这说明本文提出的FGA算法相比于SGA算法,不仅有效地提高最优解精度,而且降低了最优解的标准差。 2)采用2种算法对寻优难度大的无约束的多峰函数Rastigrin和Schwefel进行求解。由图2、表2可知,对于函数最优值附近的陡峭区域,2种算法都能精确地求得理想值,然而FGA算法能保证在20次优化过程中,最优解的均值和标准差都为0,并且相较于SGA算法具有更快的收敛速度。这说明本文提出的爆炸算子能有效地改善标准遗传算法的种群多样性和解空间的搜索能力。 3)对于带约束的函数优化,往往很难生成满足条件的初代种群,从而导致后期求解困难,然而引入爆炸算子和精英保留策略后,可以使解的搜索范围扩大,并且保证不丢失符合约束的解集,从而使求解复杂度维数降低。由表2可知,FGA算法求得的最优值能精确到1×10-8数量级,而SGA算法求得的解的标准差近似为90。这说明本文提出的FGA算法在处理高维复杂函数能近似地求得理论值,进一步体现了本文提出的改进算法具有更好的全局搜索能力。 本文在遗传算法原有运算步骤中加入了爆炸算子,爆炸算子能够通过原解集中的个体产生局部种群,增加了算法探索解空间的能力,形成了类似于“多种群”的遗传算法,使种群在进化过程中具有更强的竞争性和全局搜索能力,从而能很好地避免算法早熟;同时引入了精英保留策略与之结合,有效地防止当前群体的最优个体在下一代进化过程中被丢失和破坏,提高了算法的鲁棒性。最后采用FGA算法和SGA算法对经典测试函数进行数值优化实验对比。对比结果分析可知,无论对于单峰函数、多峰函数、无约束条件和有约束条件的函数,本文提出的FGA算法均能快速、稳定地获得全局最优解;但是,作者在实验过程中发现FGA算法耗时相对较长,还有待于进一步改进,以提高其计算效率。 参 考 文 献 [1] GOLDBERG D E. Genetic algorithm in search, optimization, and machine learning[M]. Massachusetts: Addison-Wesley Professional, 1989:2104-2116. [2] WIES R W, CHUKKAPALLI E, MUELLER-STOFFELS M. Improved frequency regulation in mini-grids with high wind contribution using online genetic algorithm for PID tuning[C]//Pes General Meeting Conference & Exposition. National Harbor:IEEE, 2014:1-5. [3] 李晔, 姜言清, 张国成,等. 考虑几何约束的AUV回收路径规划[J]. 机器人, 2015, 37(4):478-485. [4] CHAKRAVARTY S, MITTRA R. Design of microwave filters using a binary-coded genetic algorithm[J]. Microwave & Optical Technology Letters, 2015, 26(3):162-166. [5] 李雪岩, 李雪梅, 李学伟,等. 基于混沌映射的元胞遗传算法[J]. 模式识别与人工智能, 2015,28(1):42-49. [6] 王忠, 柴贺军, 刘浩吾. 关于进化遗传算法的几点改进[J]. 电子科技大学学报, 2002, 31(1):76-79. [7] DING H F, LIU X L, LIU X. An improved genetic algorithm for combinatorial optimization[C]//IEEE International Conference on Computer Science and Automation Engineering. Shanghai: IEEE, 2011:58-61. [8] 陈碧云, 韦杏秋, 陈绍南,等. 基于多种群遗传算法的电力系统多目标优化[J]. 电力系统及其自动化学报, 2015, 27(7):24-29. [9] 杜卓明, 耿国华, 徐鹏,等. 改进遗传算法在差分像运动图像实时处理中的应用[J]. 模式识别与人工智能, 2012, 25(5):879-884. [10] 程林辉, 钟珞. 求解多峰函数优化问题的并行免疫遗传算法[J]. 微电子学与计算机, 2015, 32(5):117-121. [11] NABAVI S M H, HAJFOROOSH S, HAJFOROOSH S, et al. Maximizing the overall satisfaction degree of all participants in the market using real code-based genetic algorithm by optimally locating and sizing the thyristor-controlled series capacitor[J]. Journal of Electrical Engineering & Technology, 2011, 6(4):493-504. [12] SHI K, SONG Q, LIN S, et al. An improved genetic algorithm for degree constrained minimum spanning trees[C]//Control and Decision Conference. Yinchuan: IEEE, 2016:4603-4607. [13] 瞿颜, 袁建涛, 郭陈江,等. 一种基于引向因子和反向搜索的改进遗传算法[J]. 计算机仿真, 2015,32(1):301-305. [14] 谭营, 郑少秋. 烟花算法研究进展[J]. 智能系统学报, 2014,9(5):515-528. [15] 王瑞琪, 李珂, 张承慧,等. 基于多目标混沌量子遗传算法的分布式电源规划[J]. 电网技术, 2011, 35(12):183-189.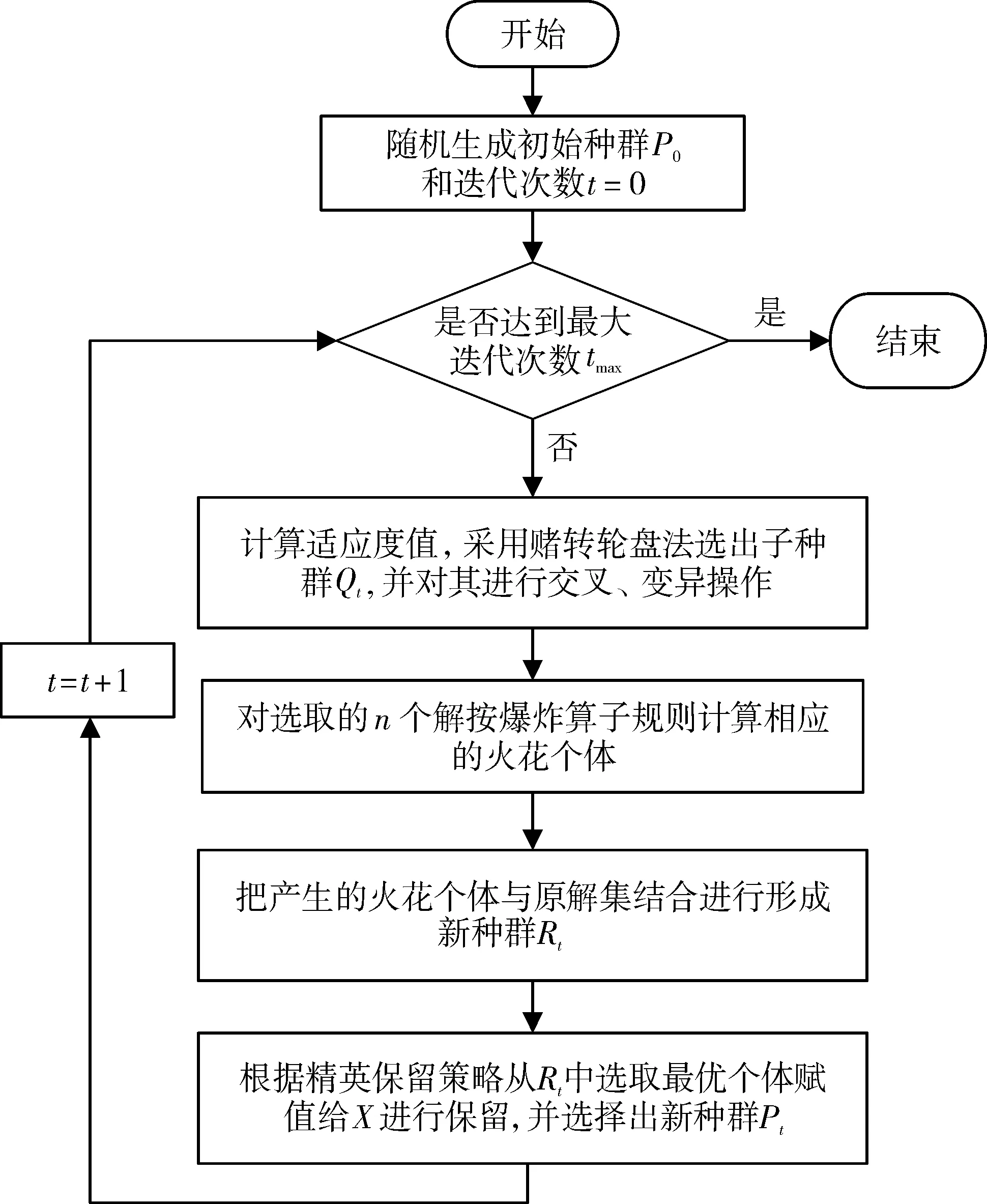
2 仿真验证
2.1 参数设置


2.2 仿真结果与分析
3 结束语

