基于动态符号执行的不透明谓词反混淆算法
宋雪勦,张 俊,何明星
(西华大学计算机与软件工程学院, 四川 成都 610039)
随着信息技术的发展,恶意软件和漏洞利用程序等层出不穷,严重危害着人们的隐私和财产安全。通常这些软件都会经过代码混淆来延长生存周期,加大了专业人员的分析难度。代码混淆方法主要包括控制流混淆、数据混淆、布局混淆和预防混淆。常见的控制流混淆包括不透明谓词混淆、控制流平展化以及指令替换等方法。
为对抗代码混淆,研究人员提出了很多反混淆的方法。马洪亮等[1]通过跟踪抽象语法树上节点的相关变量,利用相关的变量终值进行反混淆。郭军等[2]通过语义相关指令识别对混淆后程序的指令序列优化来进行反混淆。目前针对不透明谓词的反混淆方法主要是通过数据流分析对分支条件的布尔逻辑表达式进行化简来消除不可达路径[3]。当表达式依赖较多无法化简时,这种方法的有效性将大大降低。
针对以上问题,本文提出一种基于动态符号执行的路径不可达性分析来对不透明谓词混淆进行反混淆的算法。不同于数据流的静态分析,该算法通过动态分析的方式执行程序,在路径覆盖率及适应性方面都有明显的优势。
不透明谓词混淆是在原程序中加入了大量的不可达路径,因此,可以通过不可达路径分析,消除不可达路径从而达到反混淆的目的。路径敏感的程序分析是程序分析领域中的一个重要方法,其中不可达路径分析是编译优化等领域的重点研究对象之一。静态程序分析方法可以通过静态符号执行对路径约束条件进行求解,根据约束求解器的结果判断路径是否可达,然而静态符号执行分析代码混淆后的程序会使所要求解的状态空间急剧增加,导致路径爆炸。为此,本文通过动态符号执行来缓解路径爆炸问题。
1 相关工作
1998年Collberg等[4]首先提出用代码混淆的方法来保护程序的知识产权,并指出混淆转换需要依赖于不透明谓词,同时介绍了2种不透明谓词的构造方法:并发性构造和别名构造。2006年Majumdar等[5]提出通过加入大量冗余分支及不可达路径来实现控制流混淆以增加程序复杂度。2007年袁征等[6]提出利用同余方程构造一种混淆Java程序的不透明谓词簇。2013年苏庆等[7]提出了En_Logistic映射,该映射是通过改进Logistic混沌映射而来,将该映射应用到不透明谓词簇的构造过程中形成混沌不透明谓词,并应用于代码的不透明谓词混淆。
2008年Balakrishnan等[3]提出通过数据流分析来消除不可达路径,通过常量传播和可用表达式来判断指定程序点的表达式是否为常量或是否可用已计算出的值替换,以避免表达式的重复计算,对分支条件的布尔逻辑表达式进行化简,来消除不可达路径。这是一种静态程序分析方法,当表达式依赖较多无法化简时,这种方法的有效性将降低。
一方面,代码混淆使得静态程序分析的所要求解的状态空间急剧增加,出现路径爆炸问题;另一方面预防混淆能够对静态程序分析中的反汇编算法进行攻击,使得静态程序分析出错。可见,混淆程序的不可达路径分析仅仅使用静态程序分析方法是很难实现的。本文通过基于动态符号执行的不可达路径分析在一定程度上解决了路径爆炸及预防混淆对静态程序分析的影响。
2 背景知识
2.1 不透明谓词混淆
不透明谓词混淆[5]是指将不透明谓词作为基本块插入到控制流图中。不透明谓词是指在混淆过程中己经确定其输出,但是通过静态程序分析方法很难计算在某个程序点的值的谓词表达式。通过在控制流图中插入不透明谓词并将其作为分支条件的一部分,能够加大控制流混淆的强度,使得静态程序分析很难自动化地计算出输出。Collberg等[4]和袁征等[6]分别在他们的论文中给出了不透明谓词的定义。
定义1(不透明谓词[4,6]) 当程序中的一个谓词O在某个程序点P上的输出δ的一些属性在程序进行混淆时就确定了,则将该谓词O称为不透明谓词。根据其输出的不同,有3类不透明谓词:如果其值始终为true则记为OT;始终为false则记为OF;根据程序输入的不同,一部分为true,一部分为false则记为O?,如图1所示。
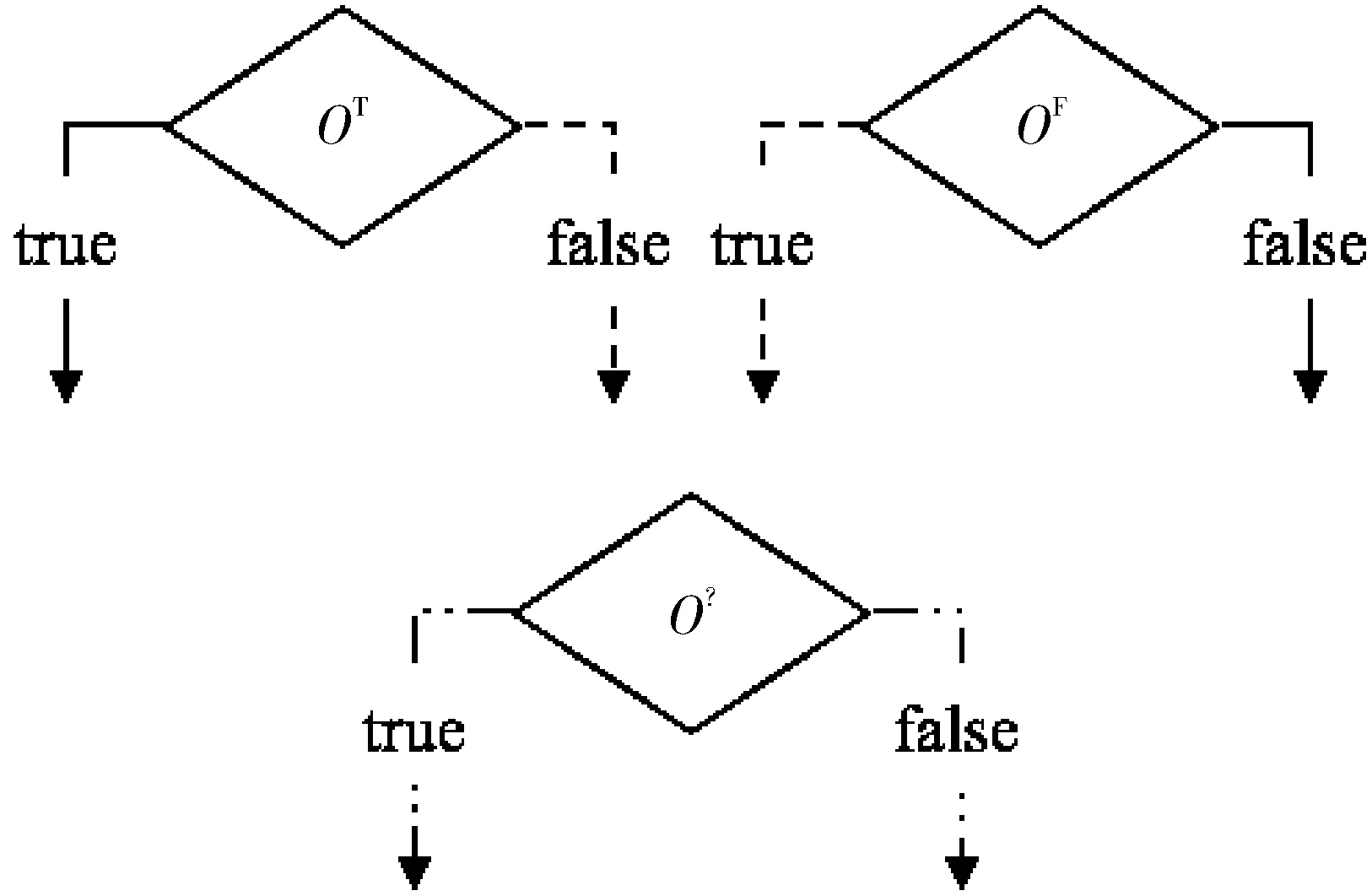
图1 3类不透明谓词
程序经过图中的不透明谓词分支后,始终执行true分支的不透明谓词,如图中的OT,其中虚线表示永远不会执行该路径,实线表示始终会执行该路径,虚实线则表示有可能执行该路径。同理,还存在不透明谓词始终会执行flase分支的OF和无法确定执行分支的O?。在提高控制流混淆强度上,不透明谓词混淆有着显著的效果。
2.2 不可达路径分析
在程序优化和编译优化领域中,消除程序中的不可达路径是一个重要目标。不可达路径分析是静态数据流分析的重要应用方向之一。将控制流图定义为有向图G=〈N,E,start,end〉,其中N表示控制流图中的节点集合,表示程序中的基本块,E表示图中边集合,若程序中有ni跳转到nj的语句,则在G中有一条从ni到nj的有向边,记为e=(ni,nj)∈E,节点start和end表示控制流的起点和终点。假设某程序路径p=〈n1,n2,…,nm〉,其中m为路径长度,ni(1≤i≤m)为程序基本块。该路径上存在k条语句为判断语句,记为集合JD={li|i=1,2,…,k}。集合中的任一语句li都对应一个判断条件ci,判断条件ci通常是由数个原子谓词及逻辑连接词组成的布尔表达式。对于路径p,其路径约束条件表达式为c1∧c2∧…∧ck。如果存在一组输入变量,使得路径条件c1∧c2∧…∧ck值为true,称路径p为可达路径;否则称为不可达路径。
2.3 符号执行
在1975年King[8]最早提出符号执行用于测试软件缺陷,可以自动化地分析程序中是否存在除0错误、空指针引用和后门等。符号执行是一种静态程序分析技术,是把输入进行符号化,基于控制流程图生成一颗符号执行树,把所有路径表示为以输入的符号为变量的约束表达式,对特定路径的约束表达式求解生成具体的输入数据。符号执行被广泛应用于不可达路径分析当中;但由于静态分析并没有实际执行,因此在遇到循环、递归等代码逻辑或者环境交互等这些在静态分析中无法确定的情况时,会出现无法生成约束的问题,导致路径爆炸。
2005年Godefroid等[9]提出动态符号执行用于动态生成测试数据。这是一种典型的结合静态分析和动态分析的混合执行技术,其主要思想是用具体执行来驱动符号执行,用一个具体的输入运行程序,并在运行过程中收集路径的约束条件,再使用约束求解器对这些约束条件取反并求解之后来生成能够执行其他路径的输入。这避免了上面提到的静态符号执行中存在的问题,因为它真实地运行了程序,能够直接执行库函数并能够跟环境交互,循坏次数和递归等都是确定的。其主要过程如图2所示。2011年Avgerinos等[10]提出了AEG符号执行引擎。这是基于符号执行分析程序源代码中潜在的栈破坏漏洞以及return-into-libc攻击方式的自动构建,以漏洞优先为路径搜索策略。2012年Cha等[11]提出了MAYHEM符号执行引擎,它是基于动态符号执行发现二进制程序中潜在的漏洞,不需要获得程序的源代码。
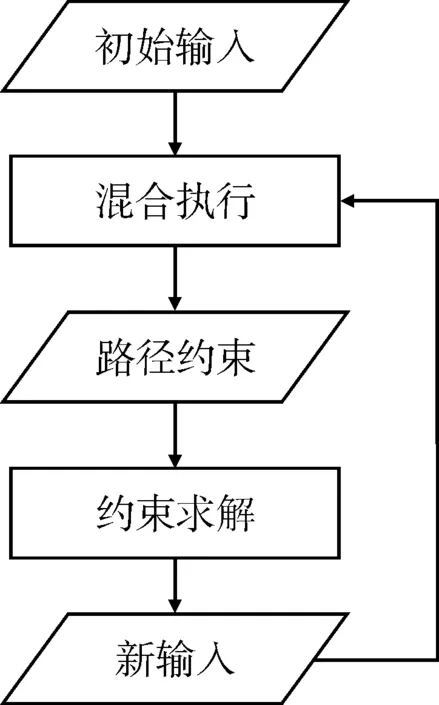
图2 动态符号执行过程
目前动态符号执行[12-15]是软件安全领域的重点研究对象之一,有非常广泛的应用前景,常见的动态符号执行软件如表1所示。由于ANGR使用了状态合并和选择符号执行等多种优化技术[16],因此本文使用此动态符号执行引擎来实现原型系统。
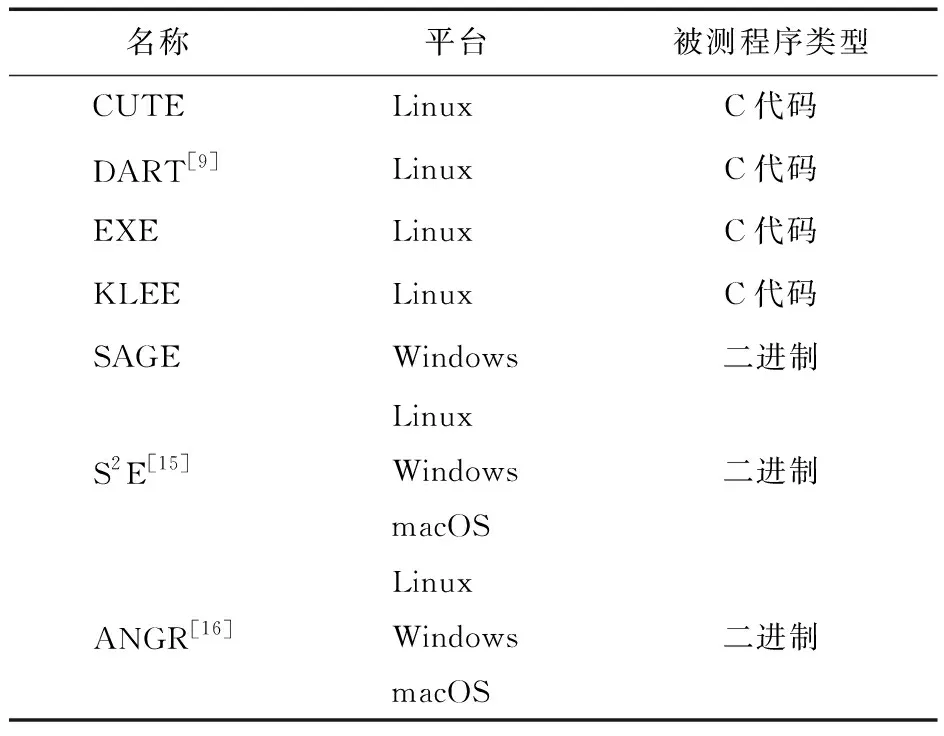
表1 常见动态符号执行软件
3 不透明谓词反混淆算法
本算法通过动态符号执行对原程序混淆后所产生的所有条件分支进行不可达路径分析,其主要思路是通过动态符号执行对不透明谓词混淆后的全部分支做路径不可达性分析,先从函数起始基本块到分支路径做动态符号执行收集路径的约束条件,然后对其进行可满足性求解,如果无解就判定分支不可达,最后把不可达的分支从程序中去除还原出原来的逻辑。如果条件分支中存在一个分支可达,但是另一个分支不可达,在这种情况下就把不可达的分支从控制流图中切除。如果2个分支都不可达或者都可达则不对其进行处理,避免在特殊情况下所带来的负面影响,例如实际代码中某些分支需要满足特定的时间条件才能进入,如果把这种分支切除就会影响原来的代码逻辑。
整个算法首先是通过控制流图分析得到每个函数的基本块,然后对含有分支的基本块进行路径可达性分析,最后进行Patch来去除不可达路径,整体流程如图3所示。
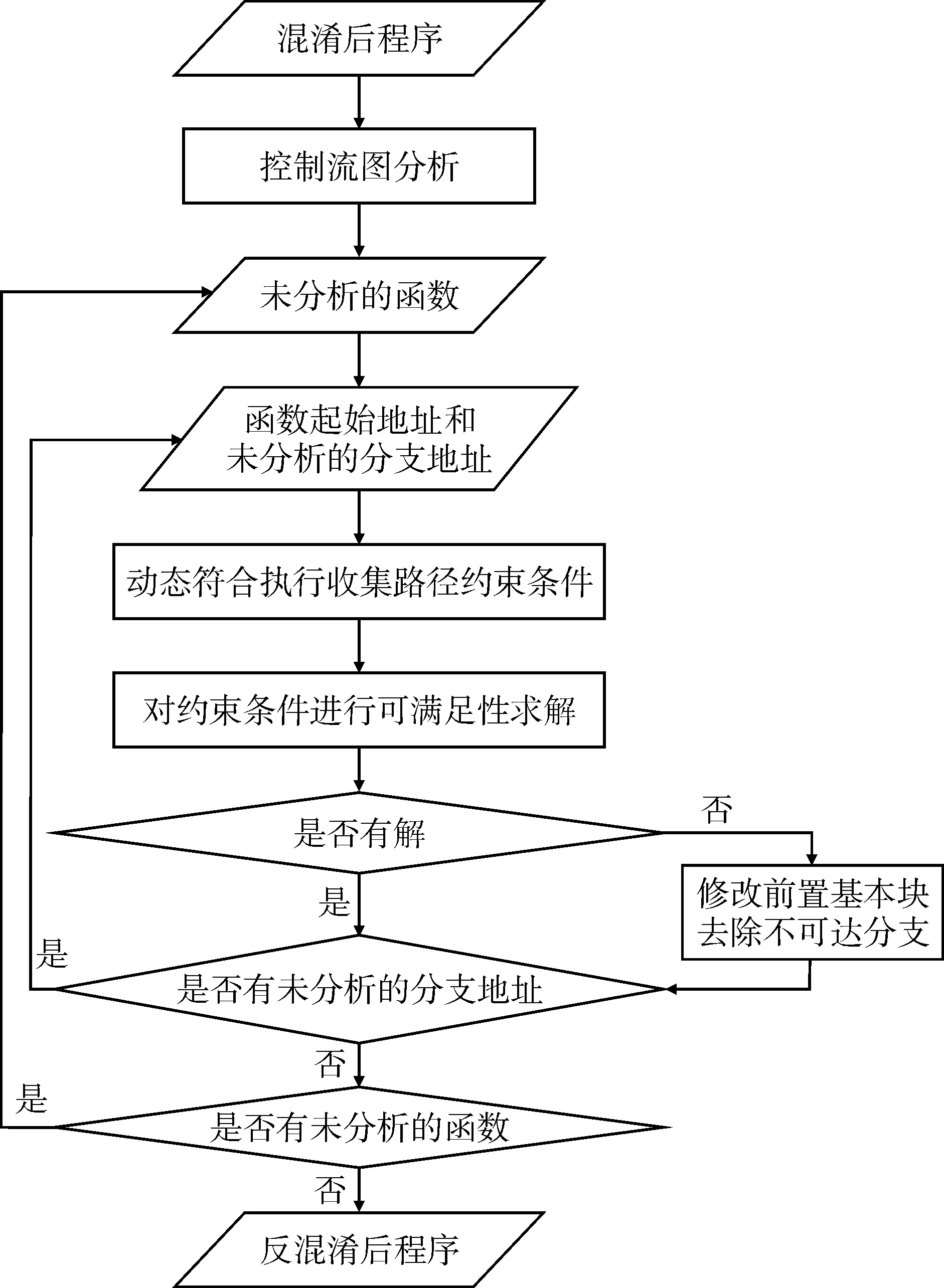
图3 反混淆算法整体流程
算法1 路径可达性分析算法PathReachability。
输入:start表示函数的起始地址;target表示条件分支的起始地址。
输出:b表示条件分支是否可达。
initSymbolicState(start,s,δ)
dynamicSymbolicExecute(target,s,δ)
IF SAT (δ) THEN
b←TRUE
ELSE
b←FALSE
ENDIF
算法1中start表示一个函数的起始地址,target表示一个条件分支的起始地址,initSymbolicState根据函数的起始地址初始化符号执行的状态空间s和路径约束集δ,接下来dynamicSymbolicExecute把一个条件分支的起始地址作为目的地址,并传入初始化后的状态空间和路径约束集进行动态符号执行,如果路径约束集有解就表示该分支可达返回true,反之返回false。
在完成条件分支的路径可达性分析后需要把不可达的分支从控制流图中切除,主要过程如算法2所示。
算法2 基本块修改算法Patch。
输入:preBlock表示条件分支前置基本块起始地址;branch表示条件分支的起始地址。
输出:preBlock表示修改后的前置基本块。
last ← getLastInstruction(preBlock)
offset ← branch-last
instruction ← newJmpInstruction(offset)
preBlock ← changeLastInstruction(preBlock,instruction)
算法2首先getLastInstruction获取一个条件分支的前置基本块的最后一条指令的地址,然后计算条件分支的起始地址与前置基本块最后一条指令的地址的偏移offset,接着newJmpInstruction根据偏移新建一条跳转的分支,并changeLastInstruction把前置基本块的最后一条指令修改成之前新建的跳转指令。
通过算法1中的路径可达性分析确定分支的可达性之后,再利用算法2修改基本块去除不可达的分支,结合这2个算法形成最终的不透明谓词反混淆算法,具体过程如算法3所示。
算法3 不透明谓词反混淆算法。
输入:p表示不透明谓词混淆后的二进制程序。
输出:pd表示反混淆后的二进制程序。
cfg ← analysisCFG(p)
reachables ← ∅
FOR function IN cfg. functions
FOR block in function. blocks
IF count(block.successors)==2 THEN
IF PathReachability(function,block.successors[0])THEN
reachables U block.successors[0]
ENDIF
…
IF count(reachables)==1 THEN
block ← Patch(block,reachables[0])
pd← apply(p,block
ENDIF
ENDIF
ENDFOR
ENDFOR
算法3首先分析不透明混淆后的二进制程序的控制流图,然后依次遍历每个函数中的每个基本块,当一个基本块有2个后继节点,即有条件分支时,对其使用PathReachability算法(算法1)做路径可达性分析,如果只有一个分支可达就使用Patch算法(算法2)把不可达分支切除,最后把修改后的基本块应用到二进制程序中。
4 实验与分析
为证明本文提出的基于动态符号执行的不透明反混淆算法的有效性,本节进行实验并分析结果。实验的操作系统为Ubuntu 16.04,内存为4 GB,CPU为2.9 GHz Intel Core i7。实验使用的混淆工具是Obfuscator-LLVM 4.0。它是一个基于LLVM IR实现的混淆工具,能够提供不透明谓词混淆、控制流平展化和指令替换的功能。测试集是coreutils 8.28软件集,原型系统使用的符号执行引擎为ANGR[16]。对测试集中的部分程序进行不透明谓词混淆后使用原型系统进行反混淆,实验结果如表2所示。
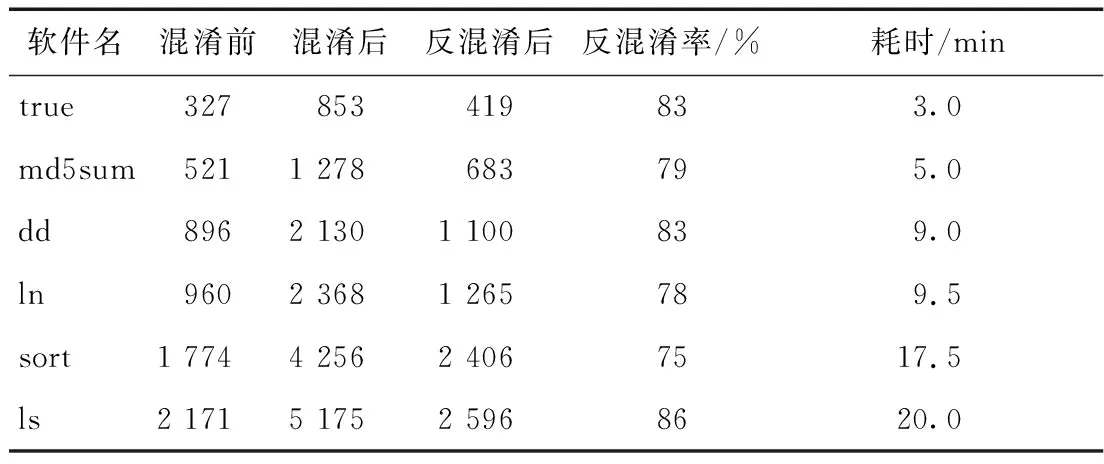
表2 反混淆前后有条件分支的基本块数量对比
由于不透明谓词混淆后会增加很多条件判断,因此,本文以含有条件分支的基本块数量来衡量反混淆率。从表中可以看出,在进行不透明谓词混淆后,有条件分支的基本块数量有了显著增加,在使用本文提出的基于动态符号执行的不透明谓词反混淆算法实现的原型系统进行反混淆后有条件分支的基本块数量明显减少,平均反混淆率为81%。这降低了混淆后的程序复杂度,有助于后续的分析工作,但是随着程序的基本块数量增加会导致性能下降,增加耗时。
5 总结
本文提出了一种基于动态符号执行的不透明谓词反混淆算法,它有效降低了经过不透明谓词混淆后程序的分析难度,减少了应急时间。后续将会在符号执行时适当使用函数摘要来提高性能,也会对控制流平展化和指令替换的反混淆算法做研究,以此来降低经过多种类别混淆后的程序的分析难度。
参 考 文 献
[1] 马洪亮, 王伟, 韩臻. 混淆恶意JavaScript代码的检测与反混淆方法研究[J]. 计算机学报, 2017, 40(7): 1699-1713.
[2] 郭军, 王蕾, 汤战勇,等. 基于语义的二进制代码自动化反混淆方法[J]. 华中科技大学学报(自然科学版), 2016, 44(3): 55-59.
[3] BALAKRISHNAN G, SANKARANARAYANAN S. SLR: Path-sensitive analysis through infeasible-path detection and syntactic language refinement [C]//Static Analysis. Heidelberg: Springer Berlin, 2008, 5079: 238-254.
[4] COLLBERG C, THOMBORSON C, LOW D. Manufacturing cheap, resilient, andstealthy opaque constructs[C]//Proceedings of the 25thACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. New York: ACM, 1998:184-196.
[5] MAJUMDAR A, THOMBORSON C. Manufacturing opaque predicates in distributed systems for code obfuscation[C]//Proceedings of the 29thAustralasian Computer Science Conference. Darlinghurst: Australian Computer Society, 2006: 187-196.
[6] 袁征, 冯雁, 温巧燕,等.构造一种新的混淆Java程序的不透明谓词[J]. 北京邮电大学学报, 2007, 30(6): 103-106.
[7] 苏庆, 吴伟民, 李忠良,等. 混沌不透明谓词在代码混淆中的研究与应用[J]. 计算机科学, 2013, 40(6): 155-159.
[8] KING J C. A new approach to program testing[J]. ACM Sigplan Notices, 1975,10(6): 228-233.
[9] GODEFROID P, KLARLUND N, SEN K. DART: Directed automated random testing[J]. Proc ACM SIGPLAN Conf on Programming Language Design and Implementation, 2005,40(6): 213-223.
[10] AVGERINOS T, CHA S K, HAO B L T, et al. AEG:automatic exploit generation[C]//Proc Network and Distributed System Security Symp. [S.l.]:NDSS, 2011:1-18.
[11] CHA S K, AVGERINOS T, REBERT A, et al. Unleashing mayhem on binary code[J]. Security and Privacy, 2012, 19:380-394.
[12] 安靖. 动态符号执行关键技术研究[D]. 北京: 北京邮电大学, 2014.
[13] LUCKOW K, DIMJSEVC M, GIANNAKOPOULOU D, et al.JD art: A dynamic symbolic analysis framework[C]//Proc 22nd Int Conf on Tools and Algorithms for the Construction and Analysis of Systems. Heidelerg: Springer Berlin, 2016: 442-459.
[14] ZHANG Y, CLIEN Z, WANG J,et al. Regular property guided dynamic symbolic execution[C]//Proc 37th Int Conf on Software Engineering, 2015,1: 643-653.
[15] CHIPOUNOV V, KUZNETSOV V, CANDEA G. The S2E platform: Design, implementation, and applications[J]. ACM Transactions onComputer Systems, 2012, 30(1):2.
[16] SHOSHITAISHVILI Y, WANG R, SALLS C,et al. SOK: (state of) the art of war: Offensive techniques in binary analysis[C]//In IEEE Symp on Security and Privacy.San Jose, CA,USA:IEEE, 2016: 138-157.
——论胡好对逻辑谓词的误读

