多轴向聚酯经编涂层织物黏弹塑形变性能

敬博洋， 赵禄鹏，敬凌霄，，蒋金华，陈南梁

(1. 吕梁学院 数学系，山西 吕梁 033000； 2. 西南大学 纺织服装学院，重庆 400715； 3. 东华大学 纺织学院，上海 201620)

涂层织物由于具有优异的力学性能，因此被广泛应用于建筑及运输等领域。在多种多样的涂层织物中，多轴向经编涂层织物相较于机织涂层织物具有平直的纤维形态，因此具有更好的力学和可设计性能[1]，从而逐渐受到人们的重视。目前对于多轴向结构复合材料的研究主要集中于对其拉伸、撕裂、剪切和弯曲等力学行为的特征和理论研究。文献[2]利用黏合剂代替捆绑纱制备了多种多轴向织物结构复合材料，并研究了此种复合材料的弹性力学行为。文献[3]研究了捆绑纱的工艺方法对多轴向织物增强材料的弯曲和层间剪切性能的影响。另外，有学者利用有限元素法和代表性体积元素法研究了多轴向织物增强材料的弹性力学行为[4-8]，以及利用高速摄像技术观察该结构材料的拉伸和撕裂过程，可以发现铺层方向和捆绑纱线对材料的力学性能有重要影响[9-11]。

随着使用时间的延长，材料受力变形会持续变大，必然影响材料的安全使用。当前，关于纺织结构复合材料依赖于时间的力学性能研究主要集中于层合板结构。文献[12]研究了碳纤维和树脂层合板结构的复合材料黏弹性特征。 文献[13]研究了亚麻聚乙烯层合板材料不同温度下的蠕变特征。

黏弹塑性行为是纺织结构复合材料的一个非常重要的性能，其关系到整个材料使用周期内的尺寸稳定性和应用范围。本文对四轴向经编涂层织物进行5个典型角度的单轴拉伸、蠕变及蠕变回复试验，并利用非线性黏弹数学模型分析预测该材料的黏弹塑变形行为。

1 试验及理论

1.1 理论模型

1.1.1 蠕变和应变回复的关系

从蠕变及回复试验原理(见图1)可知，首先是瞬时或短时间加载到恒定载荷，并保持该载荷直到时间t1，在t1时刻立刻快速卸载到载荷为0，并保持零载荷到2t1时刻[14]。在这个过程中，形变与时间之间的关系有如下特点和假设：

(1) 在接近0时刻，弹性应变瞬时增加，应力和弹性应变近似成正比例关系，弹性应变符合胡克定律。

(2) 在0时刻到t1时刻，随着时间的持续，蠕变应变逐步增加。假设蠕变应变可分为两个独立部分，分别是黏弹性应变和黏塑性应变，都随时间的持续而增加。假设黏弹性应变和黏塑性应变都不仅和时间有关，而且与施加载荷有关，并且持续时间和施加载荷对应变的影响是相互独立的。

(3) 在t1时刻，应力快速卸载到0，弹性应变瞬时回复，剩余应变为黏弹性应变和塑性应变。

(4)t1到2t1时刻是黏弹性应变的回复过程，也是黏弹性应变增加的逆过程。2t1时刻的残余应变是塑性应变，可以认为是0到t1时刻的黏塑性应变的累积结果。

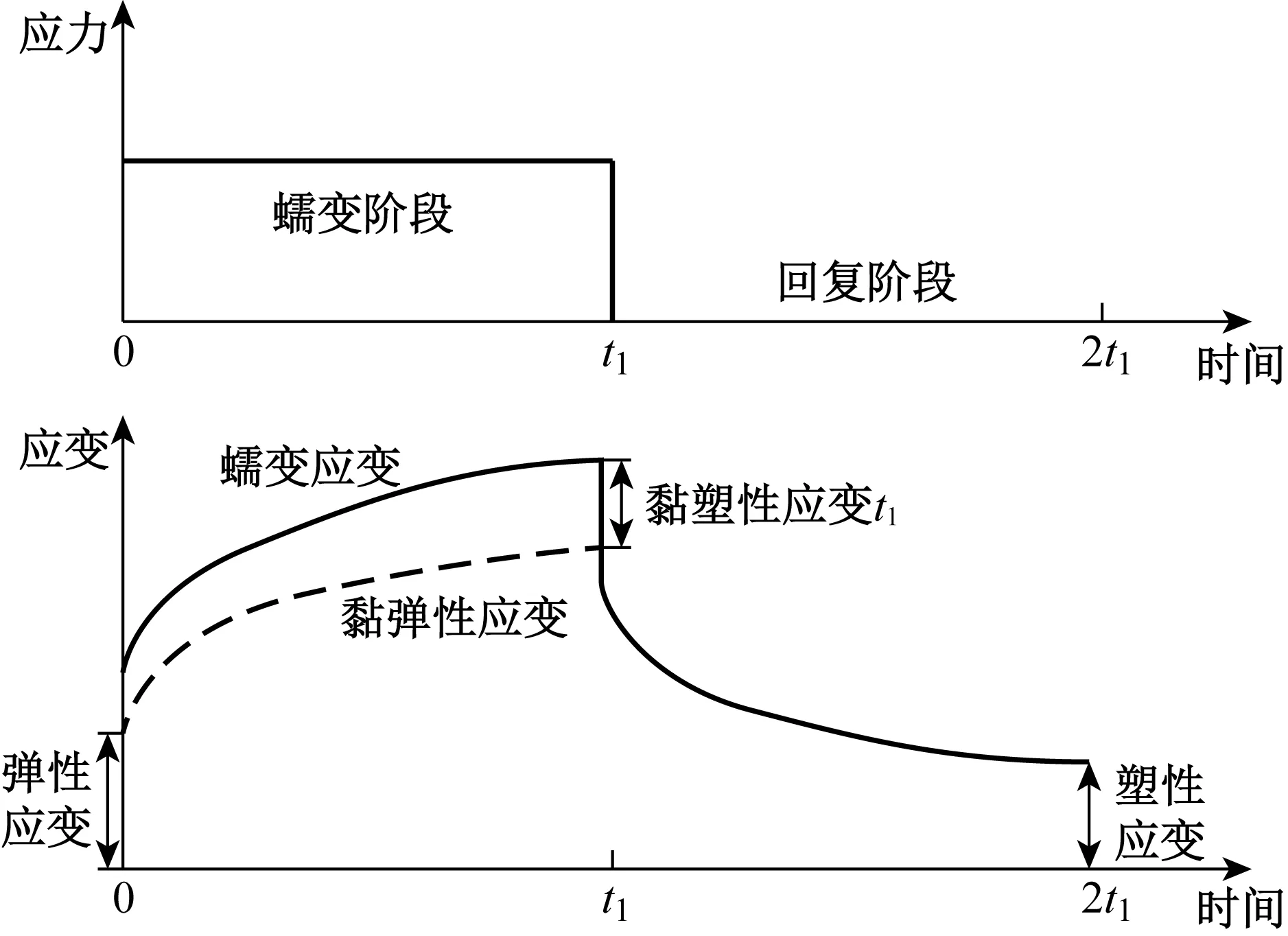
图1 蠕变及回复试验原理图Fig.1 The principle diagram of creep and strain recovery experiment

1.1.2 简化的本构方程

根据蠕变和应变回复试验理论，非线性的蠕变形变的本构方程可以表示为

εi(σ,t)=εi0(σ)+εie(σ,t)+εip(σ,t)

(1)

式中：εi(σ,t)为蠕变应变，是施加应力和保持时间的函数，图1中用实线表示;εi0(σ)为0时刻的施加应力为σ的弹性变形;εie(σ,t)为黏弹性变形，是施加应力和载荷持续时间t的函数，图1中用虚线表示;εip(σ,t)是黏塑性变形，是施加应力σ和持续时间t的函数，图1中为实线和虚线之间的差值；i表示试样的剪裁方向，i=1,2,…，5，即试样加载的5个典型角度(0°,22.5°,45°,67.5°,90°)。

其中，0到t1时刻的黏弹性变形(图1中用虚线表示)可以用t1时刻到2t1时刻的黏弹性回复曲线，即点划线来表示。黏弹性变形的回复部分，可以通过试验数据拟合得到函数表达式。黏弹性形变的本构方程可表示为

(2)

式中：εi(σ,t1)为t1时刻的蠕变应变；εie(σ,t1)为t1时刻的弹性回复应变；εir(σ,t+t1)为t1到2t1时刻的黏弹性回复应变的函数。

黏塑性变形的形式可以表示为

εip(σ,t)=f(σ)g(t)

(3)

因此，根据式(1)～(3)可将非线性蠕变变形(不考虑加载阶段的弹性变形)的本构方程表示为

(4)

1.2 试验

1.2.1 试验材料和设备

四轴向聚酯经编织物分别在0°、90°和±45°方向平铺有平直的线密度为111 tex的高强工业涤纶丝，铺层比列为1∶1∶1.4∶1.4，捆绑纱为55/72 dtex/f的涤纶丝。聚乙烯涂层织物的平均厚度为1.47 mm，平均面密度为1 687 g/m2。

沿着纤维方向0°、45°、90°和最大偏离纤维方向22.5°、67.5°裁剪试样。图2为试验材料及裁剪方向示意图。试样的规格为35 mm×140 mm，夹持间隔为70 mm，环境温度为(20±3) ℃，相对湿度为(65±4)%。

图2 试验材料及裁剪方向示意图Fig.2 Experimental materials and cutting direction image

试验采用RGM-6100型微机控制电子万能试验机，配备环境箱。 XJTUDIC三维数字散斑动态应变测量分析系统是一种光学非接触式形变测量系统，此系统用来测量试样的应变。

1.2.2 试验方法

单轴向拉伸试验。5个裁剪角度的试样均以100 mm/min的速度进行定速拉伸，测试5次。绘制出试样的应力与应变关系图，分析试样的平均最大失效应力及平均弹性模量。

蠕变及回复试验。蠕变试验，按照加载卸载试验参数执行。绘制出蠕变和回复阶段的时间-应变散点图，分析整个蠕变和回复阶段应变与时间关系及应变与试样所施加应力的关系。分析试样黏弹性应变和黏塑性应变在相同时间内不同应力水平下的变化情况，以及在相同应力水平下不同时间内的变化情况。0°、45°和90°试样以3种应力进行试验，22.5°和67.5°试样以2种应力进行试验。

2 试验结果及分析

2.1 单轴拉伸试验

单轴定速拉伸的应力-应变曲线图如图3所示，不同角度试样的平均最大失效应力如表1所示。由图3和表1可以看出，多轴向聚酯经编涂层织物的最大拉伸破坏应力与试样裁切角度之间存在密切关系。45°、90°和0°试样因为与铺层纱线平直，其最大应力均大于23 MPa，22.5°和67.5°试样最大应力接近且较小，均小于13 MPa。这是因为45°方向纱线密度约是0°和90°试样密度的1.4倍，所以45°方向的应力最大。由于聚酯纤维屈服应变大于涂层材料的屈服应变，因此沿纤维平行方向的最大破坏应变比纤维相交方向的应变大。

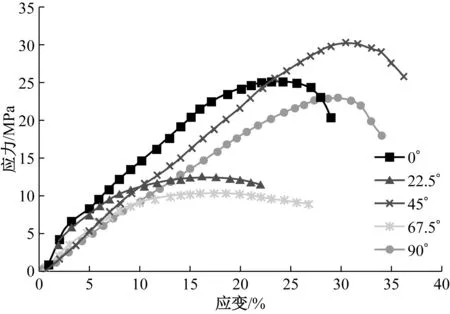
图3 单轴向拉伸应力-应变曲线Fig.3 The stress-strain curves of un-axial tensile

表1不同裁剪角度试样的失效应力

Table1ThefailurestressofspecimenswithdifferentcuttinganglesMPa

由图3可知，在定速拉伸过程中，各个裁剪方向的最大破坏应力处均为圆顶，而非尖顶，可见最大应力处为逐步破坏，属于韧性破坏。另外，从0 MPa到最大应力的80%处，各种剪裁角度的试样都表现出线弹性特性。因此，蠕变试验的加载应力均小于最大应力的80%。

2.2 加载及卸载试验

加载和卸载过程中的应力-应变关系图如图4所示。由图4可以看出，在加载和卸载过程中，随着应力的增加，应变也随之增大，应力和应变近似成正比例关系，即符合胡克定理。

(a)加载

(b)卸载图4 加载和卸载过程中的应力-应变曲线Fig.4 Stress-strain curves in the loading and unloading process

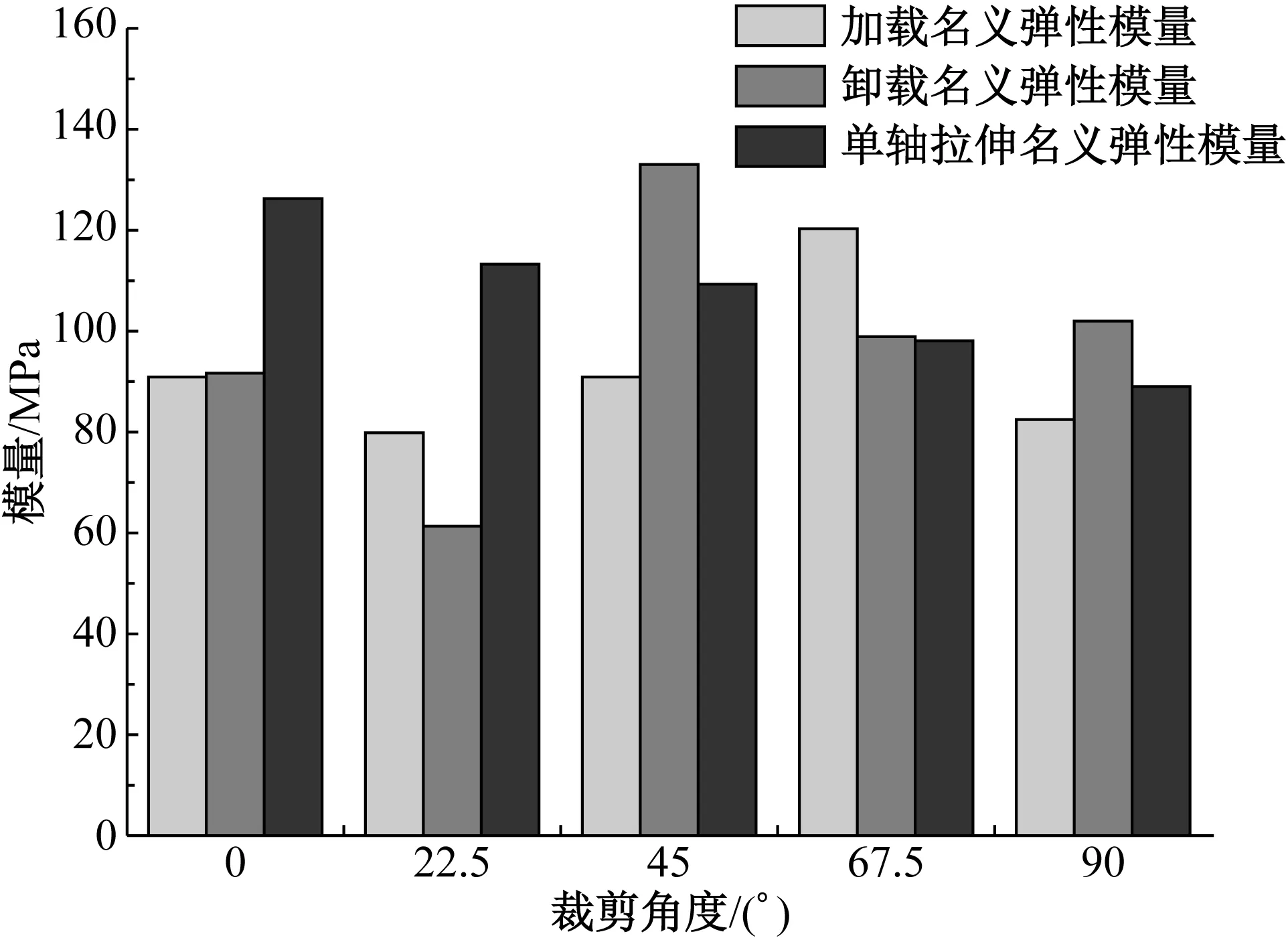
图5 加载和卸载过程中的名义弹性模量Fig.5 Nominal elastic modulus during loading and unloading process

加载、卸载和定速拉伸过程中的名义弹性模量比较图如图5所示。由图5可以看出，涂层布的加载名义弹性模量、卸载名义弹性模量和单轴拉伸的名义弹性模量各不相同。涂层布拉伸角度不同，造成拉伸时名义弹性模量的不同。0°、45°和90°时的拉伸是在有纤维增强的方向进行拉伸; 22.5°和67.5°时的拉伸则是在没有纤维增强的方向进行拉伸。0°、45°、90°卸载时模量大于加载时的模量，22.5°和67.5°卸载时模量小于加载时的模量。越接近0°，材料的单轴拉伸名义弹性模量与加载和卸载名义弹性模量的差异越大。

由此可知，导致加载和卸载过程中名义弹性模量大小不同的主要原因有二，即是否有纤维增强和织物加工工艺的不同。织物加工中整经工艺和捆绑纱的编织工艺造成卸载过程中的回弹性能不同。

大禹集团的节水灌溉产业，符合建设美丽中国的政策导向，符合广大农民增收致富的强烈愿望，大禹发展战略的调整实施，正在拉开打造世界知名百年企业的大幕。

2.3 恒定应力下的蠕变及回复试验

5个不同裁剪角度的试样按照表2的应力大小进行7 h蠕变试验和7 h回复试验。

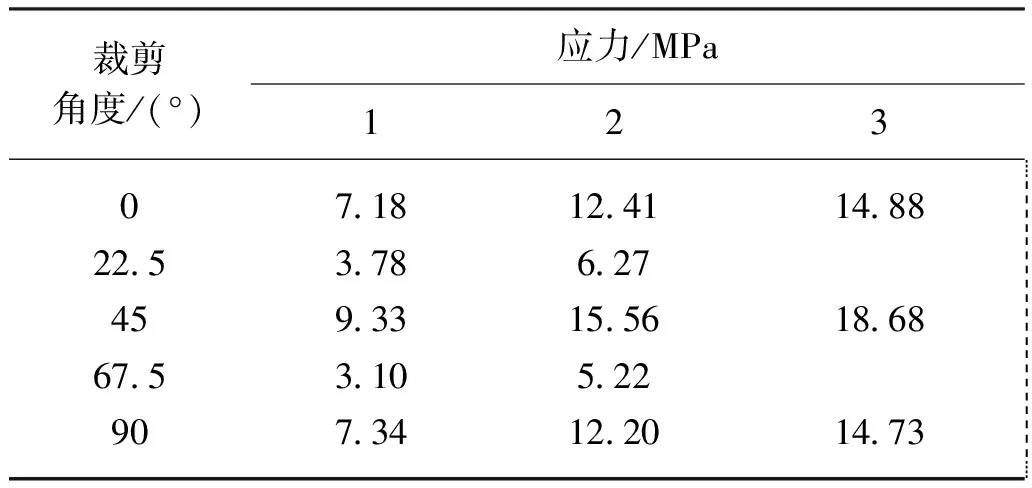
表2 不同裁剪角度试样的施加应力Table 2 The applied stress at various directions

蠕变及应变回复试验中，加载在60 s内达到设定值，卸载时间约为30 s，由于时间较短，因此加载阶段和卸载阶段的黏性应变忽略不计。

图6为蠕变及应变回复的试验结果。由图6可知，在蠕变回复试验中，应变随时间的变化可以分为4个阶段，即加载阶段、蠕变阶段、卸载阶段和回复阶段。在加载阶段，试样主要发生弹性形变，时间不超过1 min，具体应变值可由加载名义弹性模量计算得到，此过程由于时间较短，因此在图6中未标出。在蠕变阶段，试样在恒定载荷作用下同时发生黏弹性形变和黏塑性形变，持续时间约7 h。在卸载阶段，试样在保载7 h后开始卸载，卸载过程约30 s，试样主要发生弹性回复，弹性回复应变大小可由卸载名义弹性模量计算得到，与加载阶段的情况类似，此过程由于时间较短，未在图6中标出。而在回复阶段，当卸载之后，试样进入自由状态，此时主要发生黏弹性的回复变形，最终不能回复的形变即为试样的塑性形变，即蠕变阶段造成黏塑性变形的累加结果。

(a) 0°

(b) 22.5°

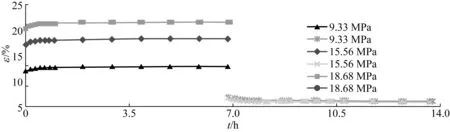
(c) 45°

(d) 67.5°

(e) 90°

2.4 黏弹性与施加应力的关系

应力与黏弹性应变大小的关系图如图7所示。由图7可以看出，涂层布的黏弹性应变和施加应力相关，随着应力的增大，黏弹性应变增大，近似成正比例关系。

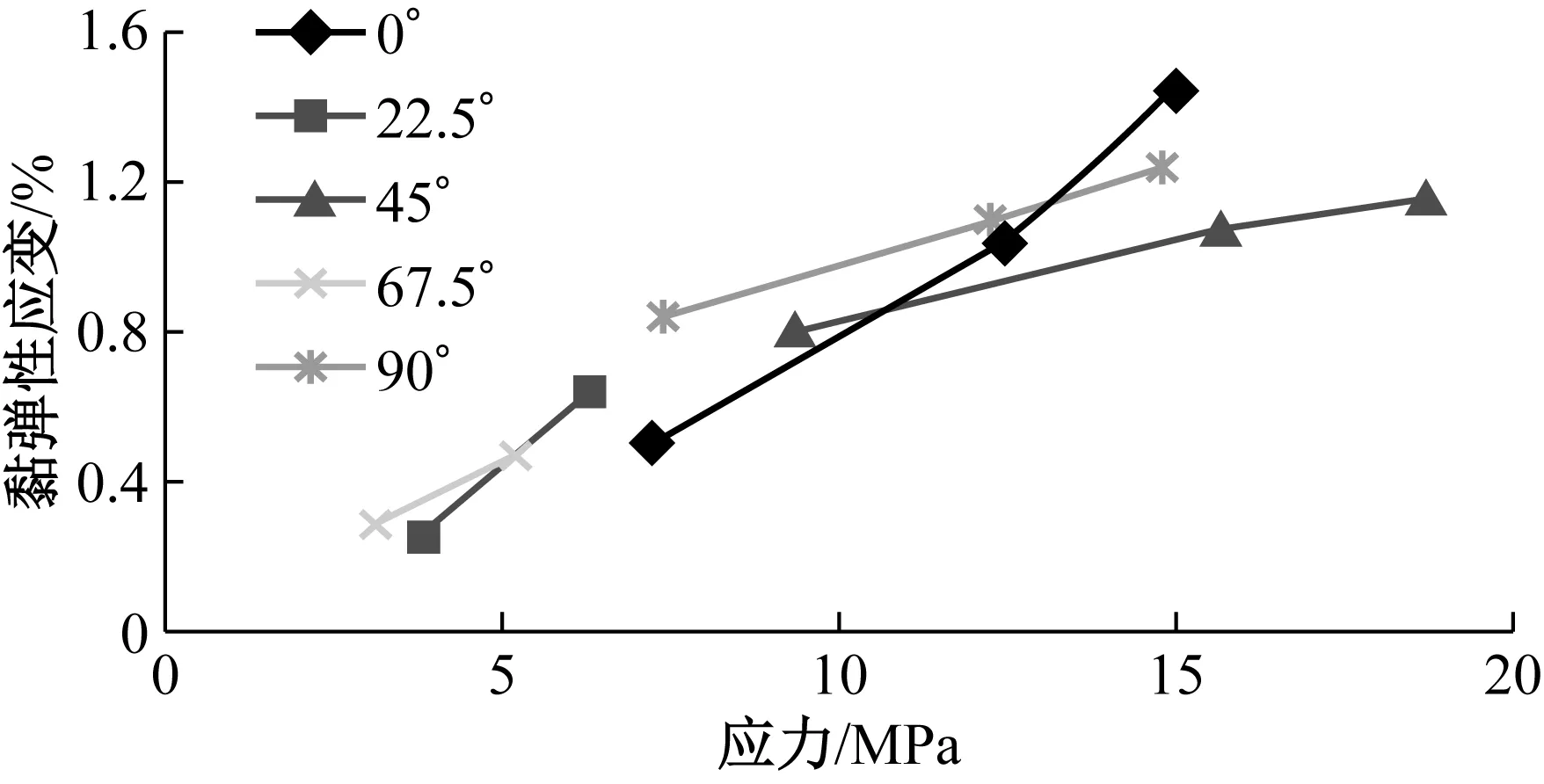
图7 应力和黏弹性应变的关系Fig.7 The relationship between stress and viscoelastic strain

2.5 不同时间的黏弹性应变试验

假设应变回复过程与黏弹性应变是互逆过程。黏弹性应变与应力的关系图如图8所示。由图8可以看出，在去除外力作用后，黏弹性应变快速下降，然后缓慢下降最终趋于平缓。其中不能回复的残余应变属于塑性形变，可以认为是蠕变阶段黏塑性变形的累加结果。涂层布的黏弹性应变和时间的关系可以用指数函数来描述。

图8 黏弹性应变和时间的关系Fig.8 The relationship between viscoelastic strain and time

2.6 不同时间的黏塑性应变试验

不同时间的黏塑性应变如图9所示。涂层布在恒定的应力作用下，不同时间的蠕变及回复试验后的残余应变可以认为是相应时间的黏塑性应变。由图9可知，所有5个角度试样的不可回复黏塑性应变均小于回复初始的变形，即小于蠕变最终的变形。残余的黏塑性应变随时间的变化特征为：初始阶段较小，然后快速增加到一定程度，后期变化较小。

2.7 黏塑性与施加应力关系

-试验数据，—-线性拟合结果图9 不同时间的黏塑性应变Fig.9 Viscoplastic deformation at different time

为了研究蠕变变形中黏塑性变形和载荷大小的关系，设计了不同应力水平下7 h蠕变和7 h回复试验。在其他条件相同的情况下，涂层布的黏塑性变形与载荷大小的关系如图10所示。由图10可知，涂层布在纤维增强方向的黏塑性变形与施加应力相关不大，而涂层布在没有纤维增强方向的黏塑性变形与施加应力密切相关，近似成正比例关系。随着应力的增大，黏塑性应变也随之增大。显而易见，应力的变化对22.5°、67.5°的黏塑性应变影响较大，对0°、45°、90°的黏塑性应变影响较小。

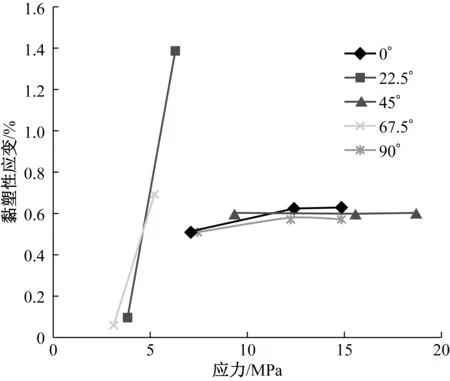
图10 不同应力的黏塑性变形Fig.10 Viscoplastic strain of various stresses

2.8 不同应力下的黏弹性与黏塑性应变的关系

蠕变应变由两部分组成：黏弹性应变和黏塑性应变。应力与黏弹性和黏塑性应变之间的关系如图11所示。由图11可知，应力对黏弹性应变和黏塑性应变有明显的影响，应力越大则应变越大。

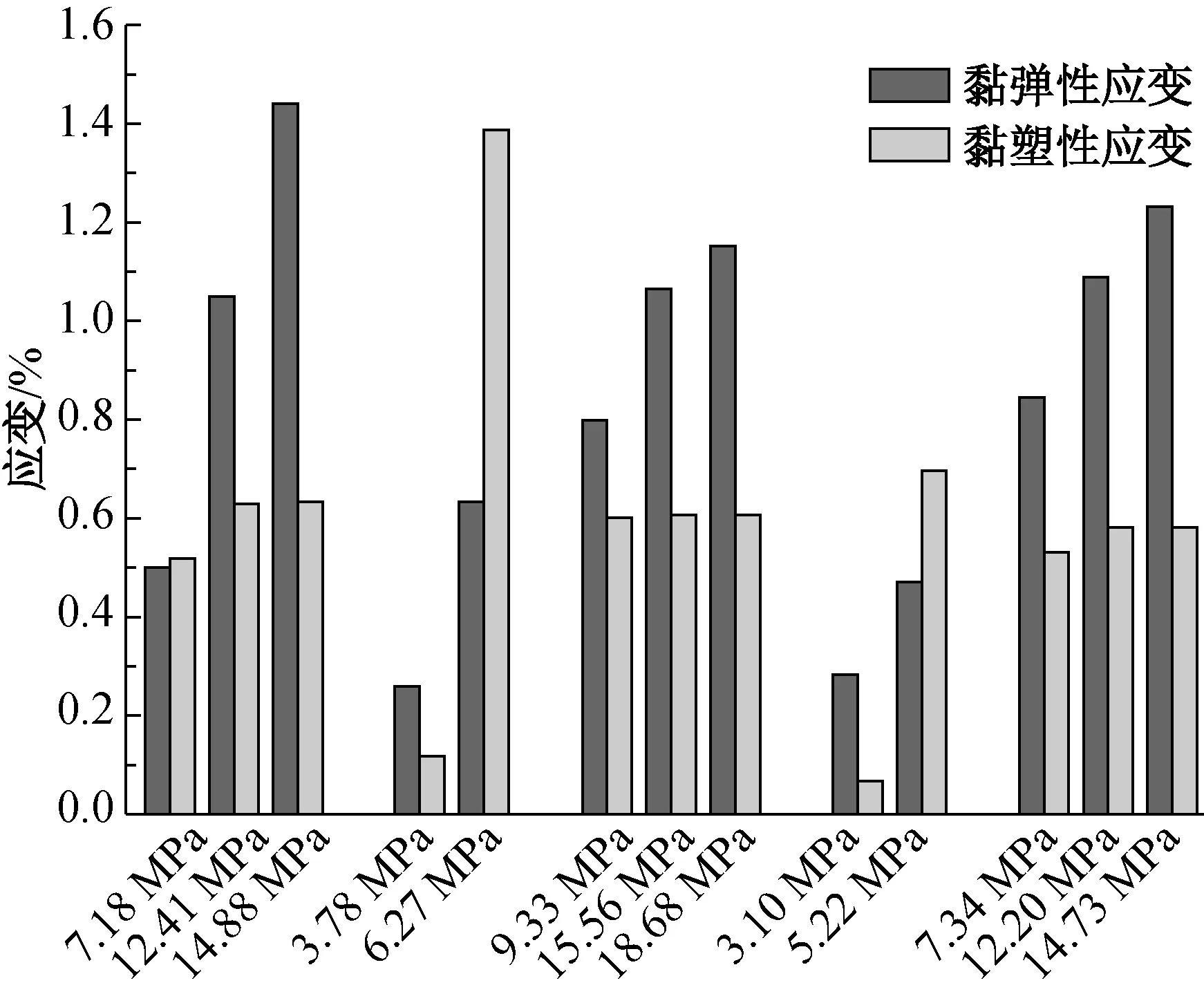
图11 不同应力下的黏弹性和黏塑性应变Fig.11 Viscoelastic and viscoplastic strain under different stresses

试样的裁切角度，即有无纤维增强对黏弹性应变和黏塑性应变也有明显的影响。对0°、45°、90°的方向施加力的作用时，应力越大，黏弹性应变比黏塑性应变的变化明显，而在22.5°、67.5°方向施加力的作用时，应力越大，黏塑性应变比黏弹性应变的变化明显。

基于变形和复合材料微观结构的特点，纤维不可避免地会发生拉伸和平面内旋转。拉伸蠕变变形的原理图如图12所示。由图12(a)可知，沿0°、45°、90°方向进行拉伸时，是在有纤维增强方向进行拉伸，只有两个方向的纤维进行拉伸旋转，黏弹性应变的大小表现比黏塑性应变明显。由图12(b)可知，沿22.5°和67.5°方向进行拉伸时，没有在纤维增强方向进行拉伸，4个方向的纤维被拉伸然后旋转，这时黏塑性应变的表现比黏弹性应变明显。

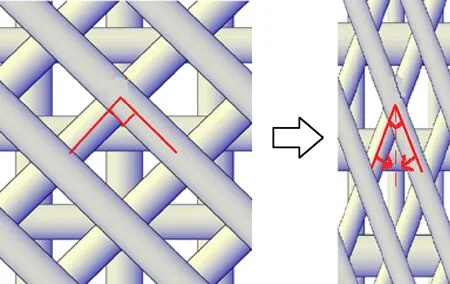
(a) 沿0°、45°和90°方向拉伸

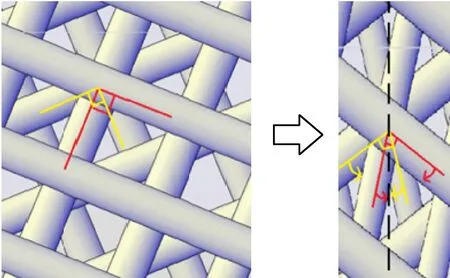
(b) 沿22.5°和67.5°方向拉伸图12 拉伸蠕变变形原理图Fig.12 Schematic diagram of tensile creep deformation

2.9 蠕变变形及预测

涂层布是黏弹塑性材料，为了研究非线性的蠕交行为，设计了不同应力水平下的7 h的蠕变试验。

蠕变试验数据和数学模型式(4)的理论数据如图13所示。由图13可知，蠕变初始阶段(小于1 h)的理论数据与试验数据之间存在偏差，但在1 h后两者呈现很好的一致性。

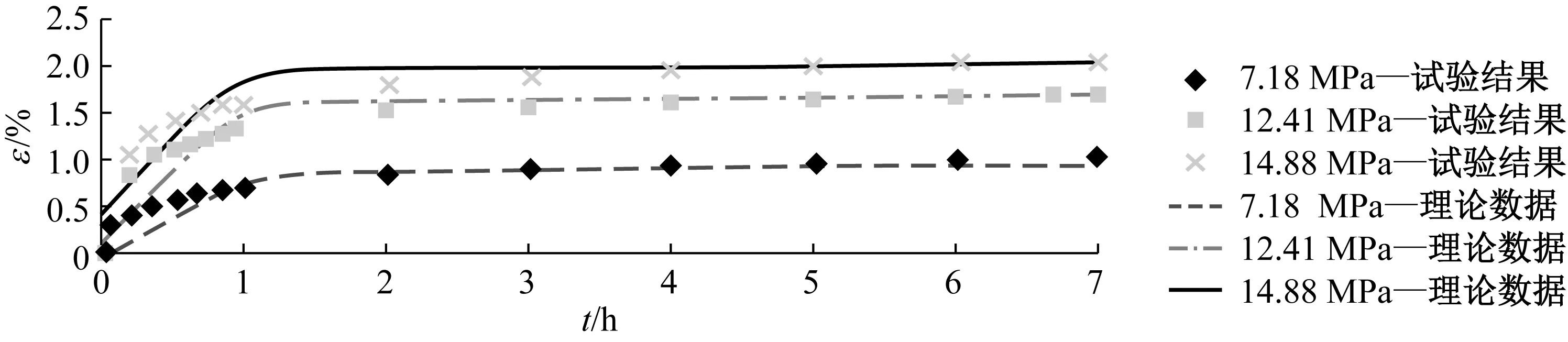
(a) 0°

(b) 22.5°

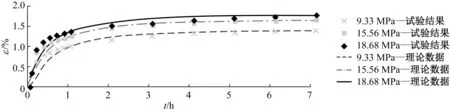
(c) 45°

(d) 67.5°

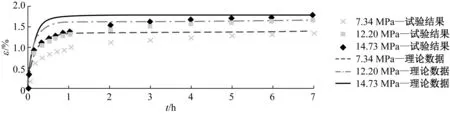
(e) 90°

3 结 语

本文通过对聚酯四轴向经编织物涂层聚乙烯柔性材料沿着增强纤维平行和不平行方向的黏弹塑性形变特征进行研究，可以得出以下结论：

(1) 单轴向拉伸时，在小于最大失效应力的80%时，应力和应变呈线性变化，该材料发生弹性形变。

(2) 研究加载和卸载过程中的试样变形特点可以发现，该涂层织物应变和应力呈线性变化，沿着纤维增强方向的卸载模量大于加载模量，在无纤维增强方向恰好相反。

(3) 该涂层织物黏弹性应变和黏塑性应变都与应力水平成线性关系，与时间成指数关系。

(4) 该涂层织物在纤维方向弹性变形约为20%，非纤维方向约为5%; 蠕变变形均在2%左右。该材料蠕变的变形在第1 h内，随后蠕变变形不明显。

(5) 非线性黏性形变模型可以很好地对该材料在不同应力水平下7 h的蠕变变形量做出预测。

参 考 文 献

[1] AJELI S，ZARREBINI M，SHARIFI H. An investigation into factors affecting mechanical properties of multi-axial nonwoven structure [J]. Journal of Industrial Textiles，2013，43(1): 45-55.

[2] AL-MONSURl M A，BARDL G，CHERIF C. Evaluation of adhesive binders for the development of yarn bonding for new stitch-free non-crimp fabrics [J]. Textile Research Journal，2015，85(15): 1635-1648.

[3] BYUN J H，WANG Y Q，KWAN L S，et al. Stitching effect on flexural and interlaminar properties of MWK textile composites [J]. Composites Research，2015，28(3): 136-141.

[4] CHUN H J，CHOI J M，BYUN J H. Stress analysis in single and multi fastened single-lap composite joints [J]. Key Engineering Materials，2006(306/308): 823-828.

[5] CHUN H J，KIM H W，BYUN J H. Elastic behaviors of stitched multi-axial warp knit fabric composites[J]. Key Engineering Materials，2006(306/307/308): 817-822.

[6] CHUN H J，RYU K S，BYUN J H. Predictions of elastic properties of multi-axial warp knitted fabric composites [J]. Advances in Fracture and Failure Prevention，2004(261/262/263): 1499-1504.

[7] CHUN H J，KIM H W，BYUN J H. Elastic property prediction of the stitched multi-axial warp knit fabric composites [J]. International Journal of Modern Physics B，2006，20(25/26/27): 4022-4027.

[8] CHUN H J，KIM H W，BYUN J H. Effects of through-the-thickness stitches on the elastic behavior of multi-axial warp knit fabric composites [J]. Composite Structures，2006，74(4): 484-494.

[9] GAO Z，JIANG G M，MA P B，et al. Tear properties and meso-scale mechanism of multi-axial warp-knitted fabric from various architectures: Studied by photography [J]. Fibers and Polymers，2013，14(11): 1953-1963.

[10] GAO Z，MA P B，JIANG G M，et al. Tensile properties and meso-scale mechanism of multi-axial warp-knitted fabrics of various structural designs [J]. Indian Journal of Fibre & Textile Research，2014，39(2): 122-129.

[11] JIANG G M，GU L Y，CONG H L，et al. Geometric model for multi-axial warp-knitted fabric based on NURBS [J]. Fibres & Textiles in Eastern Europe，2014，22(3): 91-97.

[12] ALMEIDA J H S，SOUZA S D，BOTELHO E C，et al. Carbon fiber-reinforced epoxy filament-wound composite laminates exposed to hygrothermal conditioning [J]. Journal of Materials Science，2016，51(9): 4697-4708.

[13] AMIRI A，HOSSEINI N，ULVEN C A. Long-term creep behavior of flax/vinyl ester composites using time-temperature superposition principle [J]. Journal of Renewable Materials，2015，3(3): 224-233.

[14] MEGINS M，VARNA J. Nonlinear viscoelastic，viscoplastic characterization of unidirectional GF/EP composite [J]. Mechanics of Time-Dependent Materials，2003，7(3/4): 269-290.