基于等稳定要求网壳结构截面优化设计
陈世英, 李维国, 鹿晓阳
(1.中国石油大学(华东)储运与建筑工程学院,山东青岛 266580; 2.山东建筑大学土木工程学院,山东济南 250101)
网壳结构截面优化设计的思想为离散变量优化设计,以杆件截面尺寸为设计变量,以结构质量等为目标函数,结构的强度、刚度、局部(杆件)稳定性和整体稳定性为约束条件,寻求满足约束条件且目标函数最小的杆件截面取值[1-3]。现行的空间网格结构技术规程[4]规定单层网壳结构必须进行整体稳定性验算,其弹塑性稳定承载力须大于两倍的均布外荷载。整体稳定性是单层网壳结构设计的关键问题[5-8],在优化设计过程中必须将整体稳定承载力作为约束条件充分考虑[9-10],否则无法保证优化后结构的稳定承载力安全。单层网壳结构是缺陷敏感结构,整体稳定承载力随缺陷的不同而变化显著[11-14],沈世钊等[5,15]试图寻找最不利缺陷以获得最不利的弹塑性稳定承载力,但准确找到结构的最不利缺陷分布几乎不可能[16]。长期以来,均采用一致缺陷法或随机缺陷法来解决结构的初始几何缺陷问题[17-19]。在通常的网壳结构截面优化设计“杆件分组”方式中,会将网壳结构杆件按照空间位置的对称性分成若干组[20-21],记做空间位置分组法。当整体稳定性约束条件和初始几何缺陷同时引入到截面优化设计中,通过分析发现[22],基于空间位置分组法优化后的结构仅在设定缺陷下其稳定承载力满足设计要求,在其他可能出现的缺陷下往往不能满足。可见,基于空间位置分组法的优化设计,使网壳结构的稳定承载力对缺陷分布的敏感性增加,无法保证优化后结构的稳定承载力安全。笔者结合网壳结构的截面优化设计原理提出基于等稳定要求的单层球面网壳结构截面优化设计方法,在充分考虑网壳结构杆件强度、刚度、双重非线性整体稳定性和随机初始缺陷条件下,对跨度为60 m的K6网壳结构按缺陷敏感区域进行杆件分组并进行基于序列两级优化算法的截面优化设计。
1 基于等稳定要求截面优化设计数学模型
设计变量为
x={A,Iy,Iz,Wy,Wz,ρ}.
式中,x对应一种型钢的截面属性;A为截面积,m2;Iy、Iz分别为对y、z轴的惯性矩,m4;Wy、Wz分别为对y、z轴的抗弯截面模量,m3;ρ为线密度,kg/m。
杆件分组:按网壳结构的缺陷敏感区域对杆件进行分组。
目标函数:同等用钢量情况下网壳结构稳定承载力随缺陷波动最小,表示为
minD=D(Pcr1,Pcr2,…,Pcrl) .
(1)
式中,pcri为第i个随机缺陷下结构的稳定承载力,kN/m2;l为随机缺陷个数;D为l个稳定承载力的标准差。
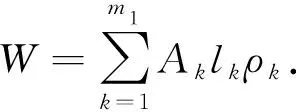
(2)
式中,W为网壳的用钢量;m1为杆件的分组数;ρk为第k组杆件的线密度;Ak为第k组杆件的横截面积;lk为第k组杆件的总长度,m。
应力约束[23]为
(3)
式中,N为杆件轴力,kN;My和Mz分别为绕y轴和z轴的弯矩,kN·m;Wy和Wz分别为两主轴的截面抗弯模量,m3;γy和γz为与截面模量相应的截面塑性发展系数,均取1.15;f为杆件的屈服应力,kPa。
弯矩作用下平面内稳定性约束为

(4)
其中
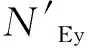
弯矩作用下平面外稳定约束为
(5)
式中,φz为弯矩作用平面外的轴心受压构件稳定系数;φb为均匀弯曲的受弯构件整体稳定系数,取1.0;η为截面影响系数,闭口截面η=0.7;βty为等效弯矩系数,取1.0。
长细比约束[4]为
λ≤[λ].
(6)
式中,[λ]为杆件的许用长细比,压杆取150,拉杆取250。
最大位移约束[4]为
Δmax≤ln/400 .
(7)
整体稳定性约束[4]为
Pcr≤2Q.
(8)
式中,Δmax为网壳结构最大节点位移,m;ln为网壳结构跨度,m;Q为网壳结构均布外载荷,kN/m2;Pcr为网壳结构弹塑性稳定承载力,kN。
2 基于离散变量的序列两级截面优化方法
约束条件按其性质可分为局部性与整体性约束两类。在截面优化过程中求解应力、长细比等局部性约束条件时采用一维搜索方法,得到满足局部约束条件的杆件截面尺寸,即第一级优化。整体性约束条件含有各个单元的设计变量,采用相对差商法[24]进行整体寻优,以第一级优化的结果作为第二级优化的初始值,反复迭代直至整体性约束条件满足。进行0阶修正可改进该算法的结果精度。
采用APDL语言编写结构建模程序、缺陷施加程序和进行弹塑性大变形分析。杆件模型采用beam189单元,屈服准则采用von Mise准则[25],材料本构关系为理想弹塑性。用FORTRAN编写基于离散变量的序列两级算法截面优化程序,通过接口程序完成FORTRAN与ANSYS的相互调用和数据交换。杆件采用热轧无缝钢管Q235,从型钢表[26]中以抗弯截面系数的升序排列为原则共提取63种型钢组成杆件截面离散集,依次编号为1#~63#,1#截面取Φ48 mm×3 mm。文中使用的杆件截面编号和对应尺寸包括:23#/Φ108 mm×4.0 mm,30#/Φ146 mm×4.5 mm,31#/Φ152 mm×4.5 mm,32#/Φ159 mm×4.5 mm,33#/Φ168 mm×4.5 mm,34#/Φ168 mm×5.0 mm,35#/Φ180 mm×5.0 mm。
3 结构缺陷敏感区域分析
网壳结构是缺陷敏感结构,许多学者对其敏感区域进行了分析[27-29]。从缺陷与稳定承载力波动关系的角度提出网壳结构的稳定承载力敏感区域,并将敏感区域与杆件分组相结合,提出了一种新的截面优化分组方法。
算例1:K6型单层凯威特网壳,跨度为60 m,矢高为15 m,环向杆件圈数为10圈;当某一个节点有缺陷时,分析结构稳定承载力值的变化规律。由于网壳结构的对称性,可仅计算缺陷出现在图1所示节点上的情况,缺陷值取跨度的1/300。单个节点存在缺陷时结构的稳定承载力变化规律见图2。

图1 1/6结构节点编号Fig.1 Node number of one-sixth structure
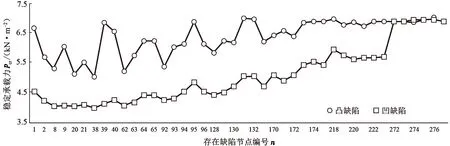
图2 单个节点有缺陷时结构的稳定承载力Fig.2 Critical-limit load under single joint imperfection
由图2可以看出,相比于凸缺陷,节点发生凹缺陷时,稳定承载力更低。其中,1#~94#节点上存在凹缺陷时,承载力低于4.5 kN/m2,94#~175#节点上存在凹缺陷时,承载力为4.5~5.5 kN/m2。175#~223#节点上存在凹缺陷时,承载力为5.5~6.5 kN/m2。272#~278#节点(支座节点)上存在凹缺陷时,承载力为6.5~7.5 kN/m2。可见,节点缺陷所处位置在壳体中上部时对结构整体稳定性影响较大;节点缺陷在壳体中部偏下时对结构整体稳定性影响较小。支座节点缺陷对结构稳定性能影响较小。
定义相同纬度的节点为一组,网壳节点可分为10组,纬度最高的一组节点定义为第一环节点(图1中,2#、3#节点所在的环),纬度最低一组节点定义为第10环节点(图1中272#~282#节点所在的环)。缺陷出现在各环节点上时结构的稳定承载力变化曲线见图3。
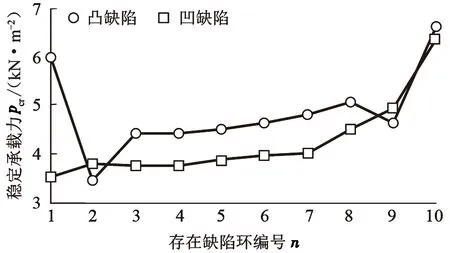
图3 十种环向缺陷下结构的稳定承载力Fig.3 Critical-limit load of structure with 10 hoop imperfections
由图3可以看出,相比于凸缺陷节点存在凹缺陷时,绝大多数情况下稳定承载力更低。考虑凹缺陷的情况,当壳体中上部节点整环出现缺陷时(1~7环),结构的稳定承载力为3.0~4.0 kN/m2,当壳体靠近支座处节点整环出现缺陷时(8~9环),结构的稳定承载力为4.0~5.0 kN/m2,当支座位置的环向节点(10环)发生缺陷时,对结构的整体稳定性承载力影响很小。
4 基于等稳定要求的网壳结构截面优化设计
网壳结构存在缺陷敏感区域,且敏感程度不同。提出了基于敏感区域的杆件分组方法,将缺陷敏感性相近区域的杆件分为一组。
算例2: 结构模型尺寸与算例1相同,外载荷Q为1.9 kN/m2,满跨均匀布置。基于结构敏感区域将杆件共分为3组(图4)。纵向所有杆件为第1组;环向杆件分为两组,1~7环杆件为第2组,8~10环杆件为第3组;基于空间位置的杆件分组见图5,杆件共分为20组。随机生成28种均值为0,均方差为R/3的正态分布随机缺陷(所有节点上均有缺陷),最大缺陷值R取跨度的1/300。
当所有杆件取相同杆件截面时(杆件不分组),在28种缺陷下网壳结构的稳定承载力(杆件截面为Φ168 mm×4.5 mm(33#))分别为5.002 4、4.064 7、4.568 7、4.596 1、3.962 1、4.459 3、4.461 8、4.801 9、3.820 4、4.298 9、4.475 8、4.596 9、4.216 4、4.138 9、4.387 5、3.758 1、4.693 7、4.391 4、4.787 2、4.297 9、4.393 4、4.823 0、4.795 7、4.724 1、4.398 9、4.418 5、4.849 4、4.734 1 kN/m2。当杆件取33#截面时,在第16组缺陷下稳定承载力不满足约束条件(3.758 1<2Q)。为提高第16组缺陷下结构的稳定承载力,全部杆件增大为34#截面,此时结构的耗钢量增大约7 t。
为对比分析未优化结构和优化结构的稳定承载力对缺陷的敏感性,按照缺陷敏感区域分组方法(图4)和空间位置分组方法(图5)对网壳结构进行截面优化设计,取第16#随机缺陷为设计缺陷。
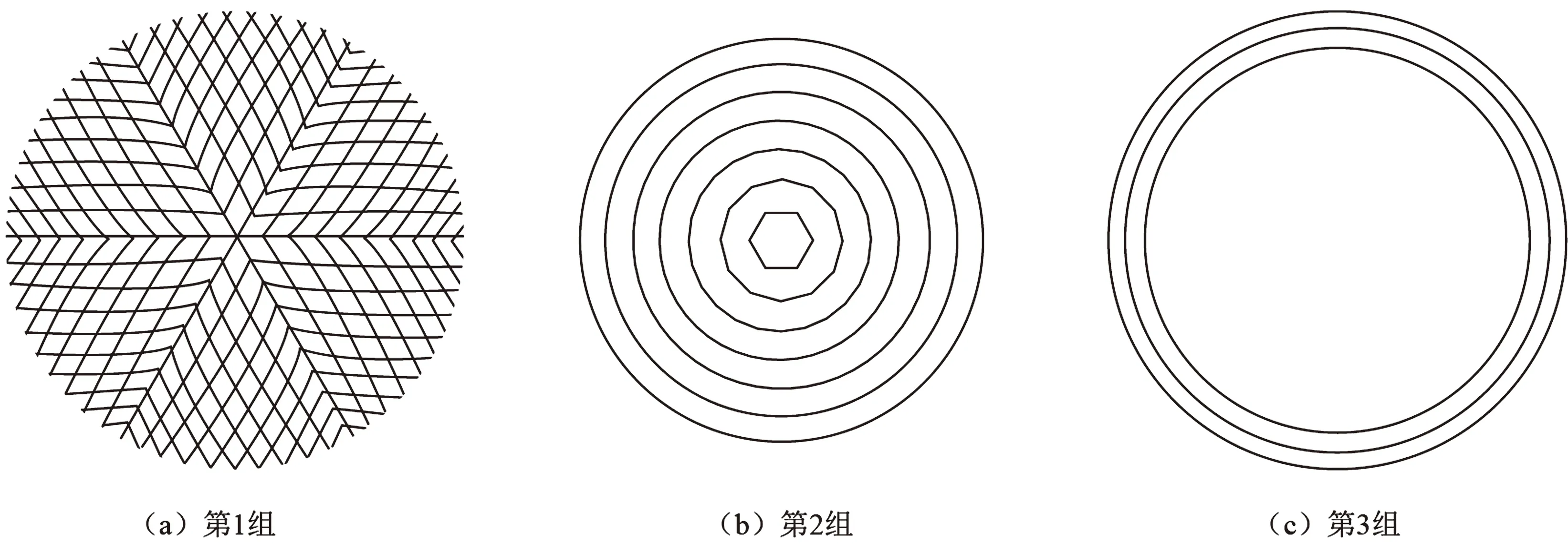
图4 基于敏感区域的杆件分组Fig.4 Group based on sensitive area

图5 基于空间位置的杆件分组(标号相同杆件同组)Fig.5 Group based on space position(bars grouped together with the same number)
采用空间位置分组方法优化后,杆件的截面取值编号为(1~20组):24#、 24#、29#、24#、33#、33#、33#、38#、33#、24#、31#、24#、31#、23#、30#、23#、30#、21#、30#、21#,在28种缺陷下的稳定承载力分别为2.895 7、2.452 7、3.529 7、2.473 7、2.723 6、2.483 9、3.185 3、2.893 2、3.223 3、2.743 3、2.497 3、2.795 3、2.182 2、2.915 9、2.706 4、3.896 9、2.542 6、2.656 1、2.976 8、2.977 6、2.736 8、3.458 7、3.261、2.510 8、2.458 3、3.173 3、3.162 3、3.275 3 kN/m2。
采用等稳定方法优化后杆件截面取值编号为(1~3组):33#、35#、23#,在28种缺陷下的稳定承载力分别为4.891 2、4.949 9、5.278 1、4.694 4、4.372 3、4.805 6、4.599 5、4.705 1、4.242 6、4.966 8、4.776 8、4.427 6、4.531 2、4.491 3、4.732 9、4.107 1、5.211 4、4.488 1、5.198 2、4.431 3、4.769 7、5.154 1、4.853 3、4.949 4、4.431 1、4.688 3、4.304 3、5.125 9 kN/m2。
采用空间位置分组方法优化得到的结构仅在设计缺陷(16#缺陷)下满足稳定承载力设计要求,在其他27种随机缺陷下,稳定承载力均小于2Q,不满足整体稳定承载力设计要求。采用基于缺陷敏感区域分组方式优化得到的等稳定结构模型,在28种随机缺陷下稳定承载力均满足设计要求。
未经截面优化、空间位置分组方法优化和等稳定方法优化得出的3种结构模型,在28种缺陷下其稳定承载力曲线见图6,稳定承载力与缺陷的敏感性关系见表1。在未截面优化、等稳定优化、空间位置优化和空间位置优化[30]情况下,不同缺陷下结构稳定承载力标准差分别为0.32、0.31、0.40和0.46,文献[30]中仅考虑了3种缺陷进行分析,本文中考虑了28种随机缺陷。
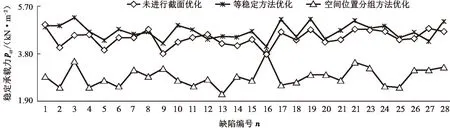
图6 三种结构模型的稳定承载力Fig.6 Critical-limit loads of three structural models
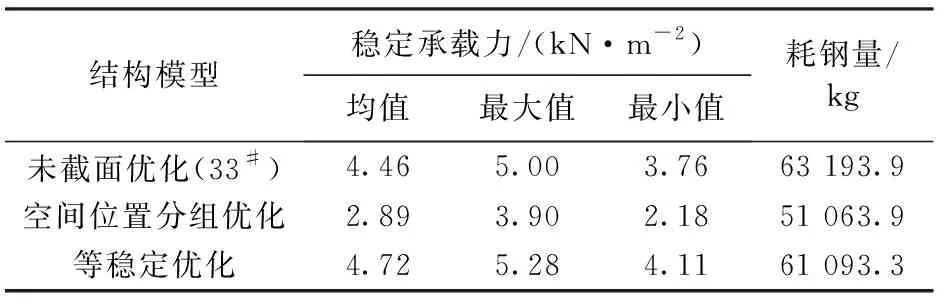
结构模型稳定承载力/(kN·m-2)均值最大值最小值耗钢量/kg 未截面优化(33#)4.465.003.7663 193.9 空间位置分组优化2.893.902.1851 063.9 等稳定优化4.725.284.1161 093.3
由图6可见,本算例中稳定承载力下限值为2Q=3.8 kN/m2。用空间位置分组优化方法得到的截面优化结果仅在16#缺陷(设计缺陷)下满足稳定承载力设计要求,在其他27种缺陷下均不能满足稳定性设计要求。未经截面优化的结构模型,当截面取值为33#截面时,16#缺陷下其稳定承载力不能满足设计要求,9#缺陷出现时其承载力也是临界满足。基于等稳定要求优化得到的设计模型,在所有缺陷下均满足稳定承载力设计要求,且有较合理的安全储备。
相比于未经截面优化设计的网壳结构,采用基于等稳定要求设计出的结构具有均值更大和均方差更小的稳定承载力。采用基于空间位置分组优化得到的结构均值小且标准差大,即优化后结构的稳定承载力对缺陷更加敏感,不能保证结构在不同初始缺陷下的稳定承载能力均满足设计要求。
5 结 论
(1)将弹塑性整体稳定承载力和随机初始几何缺陷引入到网壳结构的截面优化设计过程中,保证优化设计后的网壳结构具有足够安全的稳定承载力。
(2)在同等耗钢量下,将较大的截面分配给缺陷敏感性大的区域,较小截面尺寸分配给缺陷敏感性小的区域,确保了网壳结构在随机出现的缺陷下具有鲁棒性较强的稳定承载力。
(3)基于等稳定要求的截面优化设计方法可以使结构具有均值更大、均方差更小的稳定承载力。通常采用的基于位置分组的截面优化设计方法不能保证结构在不同初始缺陷下的稳定承载能力均满足设计要求,是不推荐采用的优化分组方法。
:
[1] SAKA M P, KAMESHKI E S. Optimum design of nonlinear elastic framed domes[J]. Advances in Engineering Software, 1998,29(7/8/9):519-528.
[2] TOKLU Y C, TEMUR R, BEKDAS G. Analysis of trusses by total potential optimization method coupled with harmony search[J]. Structural Engineering & Mechanics,2013,45(2):183-199.
[3] ABBASNIA R, SHAYANFAR M, KHODAM A. Reliability-based design optimization of structural systems using a hybrid genetic algorithm[J]. Structural Engineering & Mechanics, 2014,52(6):1099-1120.
[4] 中华人民共和国住房和城乡建设部. 空间网格结构技术规程:GJ7—2010[S]. 北京:中国建筑工业出版社, 2010.
[5] 沈世钊,陈昕.网壳结构稳定性[M].北京:科学出版社,1999:4-6.
[6] BATHE K, BOLOURCHI S. Large displacement analysis of three dimensional beam structures[J]. International Journal for Numerical Methods in Engineering, 2010,14(7):961-986.
[7] NERUBAILO B V, ZUBKOV G D, MOCHALOV M V. Stability of spirally stiffened shells under external pressure[J]. Journal of Engineering Physics and Thermophysics, 2006,9(1):202-204.
[8] 关富玲,高博青.单层网壳的稳定性分析[J].工程力学,1996,13(3):93-104.
GUAN Fuling, GAO Boqing. Stability analysis of single layer lattice domes[J].Engineering Mechanics, 1996,13(3):93-104.
[9] KHOT N S, VENKAYYA V B, BERKE L. Optimum structural design with stability constraints[J].International Journal for Numerical Methods in Engineering, 2010,10(5):1097-1114.
[10] SEDAGHATI R, TABARROK B. Optimum design of truss structures undergoing large deflections subject to a system stability constraint[J]. International Journal for Numerical Methods in Engineering, 2015,48(3):421-434.
[11] CEDERBAUM G, ARBOCZ J. On the reliability of imperfection-sensitive long isotropic cylindrical shells[J]. Structural Safety, 1996,18(1):1-9.
[12] CEDERBAUM G, ARBOCZ J. Reliability of shells via Koiter formulas[J]. Thin-walled Structures, 1996,24(2):173-187.
[13] AMAZIGO J C. Buckling under axial compression of long cylindrical shells with random axisymmetric imperfections[J]. Quarterly of Applied Mathematics, 1969,26(4):537.
[14] HUTCHINSON J W, MUGGERIDGE D B, TENNYSON R C. Effect of a local axisymmetric imperfection on the buckling behavior of a circular cylindrical shell under axial compression[J]. Aiaa Journal, 2012,9(9):48-52.
[15] KIYOHIRO I, KAZUO M. Critical initial imperfection of structures[J]. International Journal of Solids & Structures, 1990,26(8):865-886.
[16] 唐敢,尹凌峰,马军.单层网壳结构稳定性分析的改进随机缺陷法[J].空间结构,2004,10(4):44-47.
TANG Gan, YIN Lingfeng, MA Jun. Advanced stochastic imperfection method for stability analysis of single layer lattice domes[J].Spatial Structures, 2004,10(4):44-47.
[17] 徐长航,陈国明,谢静,等.基于支持向量机和蒙特卡洛的结构可靠性分析方法及应用[J].中国石油大学学报(自然科学版),2008,32(4):103-108.
XU Changhang, CHEN Guoming, XIE Jing, et al. Structural reliability analysis method based on support vector machines and Monte Carlo and its application[J].Journal of China University of Petroleum (Edition of Natural Science), 2008,32(4):103-108.
[18] 魏德敏,涂家明.单层网壳结构非线性稳定的随机缺陷模态法研究[J].华南理工大学学报(自然科学版), 2016,44(7):83-89.
WEI Demin, TU Jiaming. A probe into nonlinear stability of single-layer reticulated shells by means of random imperfection modal method[J]. Journal of South China University of Technology(Natural Science Edition), 2016,44(7):83-89.
[19] HANSEN J S. General random imperfections in the buckling of axially loaded cylindrical shells[J]. Aiaa Journal, 2015,15(9):1250-1256.
[20] LU X Y, ZHAO X W, HUANG L L. Shape optimizing design of K6 spherical reticulated shell[J]. Advanced Materials Research, 2012,424:324-329.
[21] 王法武,唐敢.考虑整体稳定的单层网壳截面优化设计[J].空间结构,2006,12(3):31-34.
WANG Fawu, TANG Gan. Sectional optimum design of single-layer lattice shells considering structural stability[J]. Spatial Structures,2006,12(3):31-34.
[22] 陈世英,张素娟,李青.初始几何缺陷对网壳截面优化结果影响研究[J].力学与实践,2015,37(6):708-712.
CHEN Shiying, ZHANG Sujuan, LI Qing. The influence of initial geometric imperfection on the section optimization result of reticulated shell [J]. Mechanics in Engineering, 2015,37(6):708-712.
[23] 中华人民共和国建设部.钢结构设计规范:GB 50017-2003[S].北京:中国计划出版社,2003.
[24] 孙焕纯.离散变量结构优化设计[M].大连:大连理工大学出版社,2002:79-85.
[25] 王新敏.ANSYS工程结构数值分析[M]. 北京:人民交通出版社,2007:435-437.
[26] 尹德钰,刘善维,钱若军.网壳结构设计[M]. 北京:中国建筑工业出版社, 1996:276-278.
[27] SCHENK C A, SCHUELLER G I. Buckling analysis of cylindrical shells with random geometric imperfections[J]. International Journal of Non-Linear Mechanics, 2003,38:1119-1132.
[28] OYESANYA M O. Influence of extra terms on asymptotic analysis of imperfection sensitivity of toroidal shell segment with random imperfection[J]. Mechanics Research Communications,2005,32(4):444-453.
[29] ROUDSARI M T, GORDINI M. Random imperfection effect on reliability of space structures with different supports[J]. Structural Engineering & Mechanics, 2015,55(3):461-472.
[30] 陈世英,李维国,李青.截面优化后网壳结构几何缺陷敏感性研究[J].空间结构,2016,22(2):16-21.
CHEN Shiying, LI Weiguo, LI Qing. Sensitivity study of geometrical imperfections of optimized reticulated shell structures[J]. Spatial Structures,2016, 22(2):16-21.

