含有执行器故障的非线性切换互联大系统的自适应模糊Backstepping容错控制

马敏 王桐 邱剑彬

摘要

本文研究了一类存在执行器故障的非线性互联切换大系统的自适应模糊Backstepping容错控制.首先定义了一个分段右连续函数作为系统的切换信号，系统依据切换信号改变模型.不失一般性，考虑执行器发生两种类型的故障，即卡死故障和失效故障，通过模糊逻辑系统逼近未知非线性函数，并设计自适应模糊容错控制器补偿执行器故障给系统带来的影响.通过Lyapunov定理证明了系统及相关变量的有界性，并基于数值仿真，验证了所提出方法的有效性.

关键词

互联大系统;切换系统;自适应模糊Backstepping控制;执行器故障;容错控制

中图分类号  TP273.4

文献标志码  A

0 引言

互联大系统[1-11] 是一类由多个子系统组成的结构复杂的非线性系统，典型特点是不同子系统之间具有互联性.由于该系统往往具有复杂性和较强的耦合性，因此互联大系统的研究具有普适性.早期对大系统的研究主要集中在线性大系统.Lee等[12-13] 研究了线性多输入多输出大系统在含有时滞情形下的稳定性问题，并得到反馈增益矩阵与系统稳定性的关系.随着分散控制思想的出现，大量学者开始研究分散控制在大系统中的应用.Hu[14] 研究了具有线性互联项的大系统的分散控制问题，通过求解Riccati方程，设计分散控制器，并给出了分散控制器与系统互联项时滞无关的充分条件.

由于实际系统中均不可避免地存在非线性元件及非线性成分，即不存在严格线性的系统，因此对非线性系统的研究更具有一般意义.文献[15-16]研究了基于Lyapunov函数递归设计状态反馈分散控制器的方法，通过反馈控制动态调节控制器最终实现系统的稳定性分析.由于实际系统中系统状态并不一定是完全可测的，文献[17-18]研究了非线性互联大系统的输出反馈镇定问题.通过引入状态观测器克服了系统状态不可测量的局限性，Yan等[18] 考虑了更为一般的时变参数大系统，所得出的结论对匹配不确定性系统及非匹配不确定性系统均具有可适性.上述文献都是基于大系统互联项精确已知的情形，若系统互联项未知，上述理论则不再适用.为了更具有一般性，Jain等[19] 研究了一类具有未知互联项的非线性大系统的稳定性问题，依据微分几何理论，将非线性互联大系统转换为一类严格反馈分散控制系统，大大降低了非线性大系统控制器设计难度，并通过自适应控制方法克服了互联项未知的问题.文献[20]研究了一类具有未知互联项的非线性大系统的自适应输出跟踪控制，采用Backstepping设计方法，解决了不满足匹配条件时的控制器设计问题;同时，引入光滑函数补偿了各个子系统分散控制器设计过程中其他子系统的影响.文献[21]研究了系统中存在更大的不确定性即存在未知非线性函数的情形，利用模糊逻辑系统逼近未知非线性函数，以此为基础设计了非线性互联大系统的自适应模糊分散控制器，保证了系统的渐近稳定性及跟踪误差的收敛性.上述文献对互联大系统的研究没有考虑到被控对象的结构由于环境因素或外界扰动变化而变化的情形，而实际系统中这种现象是普遍存在的，因此本文选择非线性互联切换大系统作为研究对象，当系统模型发生变化时，适当改变控制策略.同时，由于人为因素或使用寿命限制，在实际系统中，执行器故障运行是一种较为常见的状态.执行器的非正常运行大大降低了系统的性能，甚至可能会导致原系统不稳定，在实际生产中，可能带来巨大的经济损失，因此有必要在执行器发生故障时，对故障进行补偿和抵消，从而使系统恢复到原始的正常运行状态，容错控制便是可以实现这一功能的控制方法. 因此，在本文中，基于非线性互联切换大系统设计了自适应模糊分散控制器.

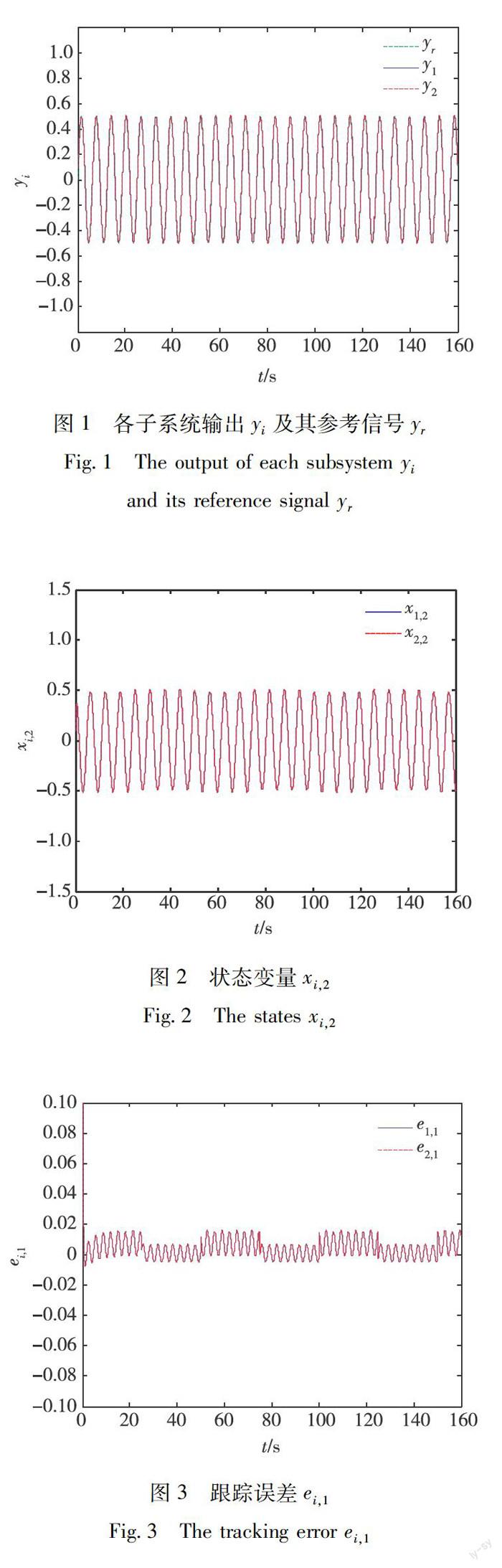
假设t>10  s ，执行器发生卡死故障，  s 1，g =  s 2，g =0.02;t>20  s ，剩余执行器发生失效故障，ρ s 1，g =ρ s 2，g = 0.5，ψ s 1，g =ψ s 2，g =1.可得仿真结果如图1—12所示，其中，图1—3分别展示了两个子系统输出及其参考信号轨迹曲线、状态变量x i，2 轨迹曲线、跟踪误差轨迹曲线.图4及图5分别展示了子系统1及2的执行器卡死与失效输出曲线，图6及图7分别展示了子系统1及2的控制器输出曲线，图8及图9分别展示了子系统1及2中自适应参数  1，2 、  2，2 的变化曲线.若执行器发生故障时，系统未采取容错控制策略，两个子系统的输出轨迹曲线及其对应的跟踪误差曲线分别如图10和图11所示，本文中采取的切换信号σ（t）如图12所示.

由图1—3可知，在如式（53）所示的自适应模糊控制器及如式（54）所示的自适应率的作用下，各个子系统的输出 y i可以较好地跟踪参考信号y r且跟踪误差e i，1 收敛到原点的小邻域内，各子系统状态变量x i，2 有界;由图6—9可知，两个子系统的控制信号u i，0 ，两个子系统的自适应参数  i，2  均有界.由未采取容错控制的各子系统输出及跟踪误差曲线图10及图11可知，各子系统输出发散、跟踪误差发散，相应子系统不稳定.由上述仿真结果可知，本文所提出的 控制器对于一类含有执行器故障的非线性切换互联大系统具有良好的控制效果.

4 結论

本文针对一类含有执行器故障的非线性切换互联大系统设计了自适应模糊Backstepping分散控制器.首先引入一个分段常数信号用来表示系统模型的切换，并考虑了两种类型的执行器故障：执行器卡死故障和执行器失效故障，分别对以上两类故障进行补偿，使得系统维持在故障前的稳定运行状态.同时考虑到各个子系统之间的互联对系统性能的影响，在各子系统控制器设计过程中，附加相关的补偿项，抵消了互联项对系统的影响.文中依据模糊逻辑系统的“万能逼近”特性逼近系统中的未知非线性函数，设计了自适应模糊控制器，通过选择恰当的Lyapunov函数分析得到，在自适应模糊控制器的作用下系统所有变量有界.最后通过数值仿真验证了上述理论的有效性.

參考文献

References

[ 1 ] Spooner J T，Passino K M.Adaptive control of a class of decentralized nonlinear system[J].IEEE Transactions on Automatic Control，1996，41（2）：280-284

[ 2 ] Hua C C，Ding S X.Model following controller design for large-scale systems with time-delay interconnections and multiple dead-zone inputs[J].IEEE Transactions on Automatic Control，2011，56（4）：962-968

[ 3 ] Tong S C，Li Y M，Jing X J.Adaptive fuzzy decentralized dynamics surface control for nonlinear large-scale systems based on high-gain observer[J].Information Sciences，2013，235（20）：287-307

[ 4 ] Fan H J，Han L X，Wen C Y，et al.Decentralized adaptive output-feedback controller design for stochastic nonlinear interconnected systems[J].Automatica，2012，48（11）：2866-2873

[ 5 ] Li J，Chen W S，Li J M.Adaptive NN output-feedback decentralized stabilization for a class of large-scale stochastic nonlinear strict-feedback systems[J].International Journal of Robust and Nonlinear Control，2011，21（4）：452-472

[ 6 ] Zhou Q，Shi P，Liu H H，et al.Neural-network-based decentralized adaptive output-feedback control for large-scale stochastic nonlinear systems[J].IEEE Transactions on Systems Man and Cybernetics，Part B，2012，42（6）：1608-1619

[ 7 ] Tong S C，Li Y M，Wang T.Adaptive fuzzy decentralized output feedback control for stochastic nonlinear large-scale systems using DSC technique[J].International Journal of Robust and Nonlinear Control，2013，23（4）：381-399

[ 8 ] Lin W W，Wang W J，Yang S H.A novel stabilization criterion for large-scale T-S fuzzy systems[J].IEEE Transactions on Systems，Man，and Cybernetics，Part B，2007，137（4）：1074-1079

[ 9 ] Chen B S，Wang W J.Robust stabilization of nonlinearly perturbed large-scale systems by decentralized observer-controller compensators[J].Automatica，1990，26（6）：1035-1041

[10] Wang W J，Lin W W.Decentralized PDC for large-scale T-S fuzzy systems[J].IEEE Transactions on System，2005，13（6）：779-786

[11] Liu X，Zhang H B.Stability analysis of uncertain fuzzy large-scale system[J].Chaos，Solitons & Fractals，2005，25（5）：1107-1122

[12] Lee T N，Radovic U L.General decentralized stabilization of large-scale linear continuous and discrete time-delay systems[J].International Journal of Control，1987，46（6）：2127-2140

[13] Lee  T N，Radovic U L.Decentralized stabilization of linear continuous and discrete-time systems with delays in interconnections[J].IEEE Transactions on Automatic Control，1988，33（8）：757-761

[14] Hu Z.Decentralized stabilization of large scale interconnected systems with delays[J].IEEE Transactions on Automatic Control，1994，39（1）：180-182

[15] Gavel D T，Silijak D D.Decentralized adaptive control：structural conditions for stability[J].IEEE Transactions on Automatic Control，1989，34（4）：413-426

[16] Xie S，Xie L.Decentralized stabilization of a class of interconnected stochastic nonlinear systems[J].IEEE Transactions on Automatic Control，2000，45（1）：132-137

[17] Saberi A，Khalil H.Decentralized stabilization of interconnected systems using output feed-back[J].International Journal of Control，1985，41（6）：1461-1475

[18] Yan X G，Dai G Z.Decentralized output feedback robust control for nonlinear large-scale systems[J].Automatica，1998，34（11）：1469-1472

[19] Jain S，Khorrami F.Decentralized adaptive control of a class of large-scale interconnected nonlinear systems[J].IEEE Transactions on Automatic Control，1997，42（2）：136-154

[20] Zhou  J，Wen C.Decentralized backstepping adaptive output tracking of interconnected nonlinear systems[J].IEEE Transactions on Automatic Control，2008，53（10）：2378-2384

[21] Tong S，Liu C，Li Y，et al.Adaptive fuzzy decentralized control for large-scale nonlinear systems with time-varying delays and unknown high-frequency gain sign[J].IEEE Transactions on Systems，Man，and Cybernetics，Part B，2011，41（2）：474-485

[22] Wang L X.Adaptive fuzzy systems and control：design and stability analysis[M].Englewood Cliffs，NJ：Prentice Hall，1994

Adaptive fuzzy backstepping fault-tolerant control for nonlinear large-scale

interconnected switched systems with actuator failures

MA Min 1 WANG Tong 1 QIU Jianbin 1

1 The Research Institute of Intelligent Control and Systems，Harbin Institute of Technology，Harbin 150001

Abstract  Adaptive fuzzy backstepping fault-tolerant control for a class of nonlinear large-scaleinterconnected switched systems with actuator failures is investigated in this paper.The system switches dynamically according to a piecewise right continuous function.Without loss of generality，stuck faults and the faults loss of effectiveness are considered.Fuzzy logic systems are utilized to approximate the unknown nonlinear functions.Considering the actuator failures，an adaptive fuzzy fault-tolerant controller is designed.It is proved that the proposed control method can guarantee that all the signals of the closed-loop system are bounded according to the Lyapunov theorem.A simulation example is presentedto demonstratethe effectiveness of the proposed control strategy.

Key words  interconnected large-scale systems;switched systems;adaptive fuzzy backstepping control;actuator failures;fault-tolerant control