第二十五讲 有上下限约束的混料均匀设计
徐静安 段敏伟 罗 勇
混料试验的应用范围广泛,但是笔者阅读到的案例大都采用传统的单配方考察,效率较低、实验工作量较大。跟踪的研发项目采用试验设计虽有成功,也有一些结果似是而非,困惑多年。
2014年6月8 日(周日),中石化上海石化研究院党委书记兼副院长杨为民派车接我到高桥,对分子筛催化剂项目进行预答辩评审(事后获悉,项目荣获2014年度国家技术发明二等奖)。讨论过程中得知他们采用传统的单配方筛选,在专业理论指导下,经过大量实验,取得了创新性成果。为此,他们正引进美国硅谷某公司48通道高通量的配方筛选评价装置,是除埃克森·美孚公司外的世界第二套同类装置,价值约为5000万元。又据了解,16通道的高通量配方评价装置价值约为1000万元。上海有的科研单位、化工企业已建催化剂评价中心,配置单通道的微反评价装置10余套,以加强混料配方的筛选及评价能力。
此类信息对我触动很大,除了加强硬件投入外,我们能否用软件,用数字化技术来提高研发效率,水平?!工欲善其事,必先利其器。当代科技,硬件、软件都是“器”。
下决心再学习,读了几本专著,精读了有关混料试验设计的章节,解读了几个案例,参与了上海化工研究院当前两三个混料试验项目的讨论和成功实施,有了新的感悟。就像打开了一扇窗。混料试验设计是试验设计领域的一个重要分支,这是一片新的天地。
混料试验包括混料化学反应、混料物理改性、混料生化发酵等混料组分数P≥3,组分百分比之和∑Xi=1的试验问题。其最突出的特点是∑Xi=1的约束,使各个组分分量不独立!所以既不能直接使用我们熟悉的用于独立变量的正交设计、均匀设计等试验设计;也不能简单地通过偏导数等于零的求极值方法对统计模型的组分变量Xi预报最优配方组合。
大多数试验设计数理统计专著中均未明确指出正交设计、均匀设计等不适用于非独立变量,而在书中还似是而非地引用了混料试验案例,产生了“误导”。只有少部分比较深入的专著中,才讨论混料试验,提出了混料试验的约束∑Xi=1的数学表述。而如此简明的数学表述,其内涵,其对试验设计,统计分析带来的特殊影响,我们工程科技人员在初步涉及时并未引起应有的重视。
对混料试验问题,忽视∑Xi=1的约束,研发工作将仍在困惑中摸索。
鉴于此,本讲座结合项目,对涉及混料试验的主要方法分别进行讨论。
本讲座对于有上、下限约束的混料均匀设计进行讨论。由于不能转换为正单形,在约束条件下形成多维空间的凸几何体,试验点空间变得复杂。前几讲讨论的从独立变量均匀表Un(nl)变换成不独立变量混料均匀设计表UMn(np)的方法不能直接应用。对非数学专业的工程科技人员来说,阅读数学描述的过程是有点困难的,但物理概念的理解是可能的。
为了能图示实验点形象,引用《均匀设计与均匀设计表》(方开泰著)中的案例。有一个三组分(P=3)的配方,X1=70%,X2=20%,X3=10%,为了提高质量,希望寻求新的配比。要求设计一个有上下限约束的试验:
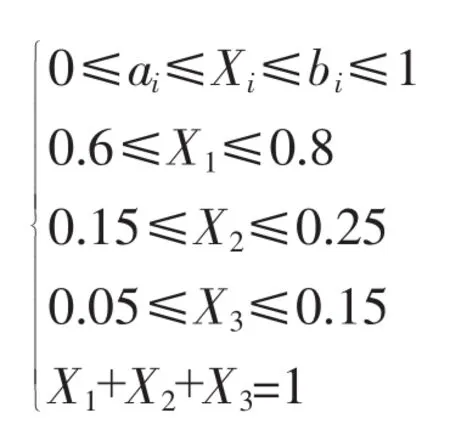
这是典型的有上、下限约束的混料配方试验。P=3是最简单的混料问题,但构筑一个混料均匀设计却是麻雀虽小,五脏俱全,变换过程有点复杂。
一、混料问题预处理
1,首先按第二十一讲“混料配方研究中极端顶点设计的应用解读”中对混料问题考察区域作出初步判断。P个组分,考察区域点集TP(a,b)非空(即存在符合要求的配方)的充分必要条件为:
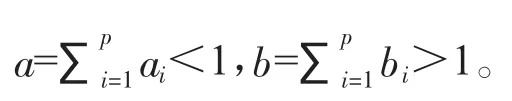
本案例a=0.8<1,b=1.2>1,点集TP(a,b)非空。但a,b的值接近1,考察区域的空间范围不是很大。如果没有上下限约束,点集TP(a,b)考察区域为:a=0,b=P。
2,其次对约束是否多余进行分析,由于混料配方组分的上、下限约束是由专业知识初选的,在正单形坐标系中,可能带有多余的约束。令:
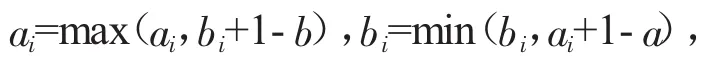
经计算,案例不存在多余的约束。
3,再按第二十二讲“混料均匀设计简介”中对上下限约束是否能形成正单形进行计算。形成正单形的上、下限约束应满足条件:
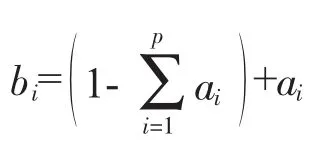
经计算,b1=0.8,b2=0.35,b3=0.25。可见,b2,b3均大于实际约束,不能形成正单形,考察区域是个凸几何体,不能直接应用UMn(np)表。顺便提及,如果b2,b3的上限约束在工程专业上不是那么严格,允许适当调整的话,还是按正单形调整为宜,略为扩大了考察范围,也简化了相应的处理。
二、混料均匀试验设计方案构筑简述
以案例P=3的混料试验为例。可供选择的试验设计方案:
(1)选择经典的混料极端顶点设计——《上海化工》2018年第1期;
(2)调整约束选择正单形的混料均匀设计——《上海化工》2018年第2期、《上海化工》2018年第4期;
(3)编制P-1个组分比率选择混料比率均匀设计——《上海化工》2018年第3期、《上海化工》2017年第4期;
(4)选择有上下限约束的混料均匀设计——《上海化工》2018年第5期。
以本案例P=3为例,简述构筑有上下限约束的混料均匀设计过程,有兴趣的读者可阅读《均匀设计与均匀设计表》。
案例:
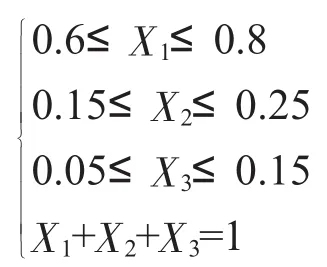
假设选取独立变量的U21*(217)均匀表,P-1=3-1=2,选使用表中第1列,第5列进行变换,变换区域及计算在《上海化工》2018年第2期已经描述,不重复展开。即可得:
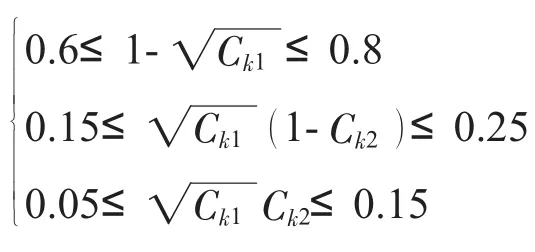
可将约束转换成:
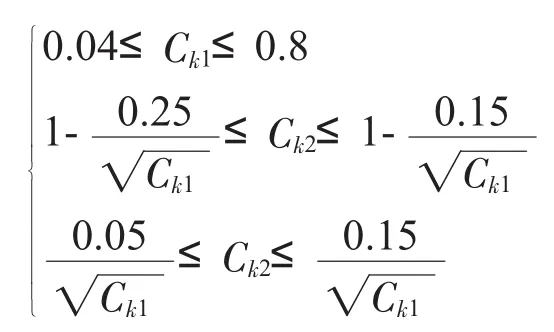
可以求得满足约束的点集区域D落于R之中。在R之中构筑的均匀设计,其中落在D区域的点也可看作在D上的一个均匀设计。图1形象地描述了数学变换的物理概念。
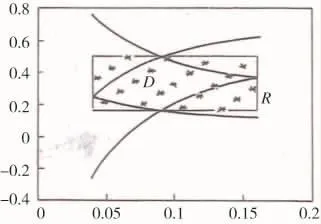
图1 区域D和R
现在问题是独立变量的U21*(217)均匀表中第1、5列转换成组分不独立的混料均匀设计,由于上、下限约束,不能形成正单形,体现在图上有些点在R中,但不在满足约束的区域D内,如果能形成正单形,区域D等价于区域R。进一步的变换和判别,才能形成本案例在区域D内的混料均匀试验方案,见表1。
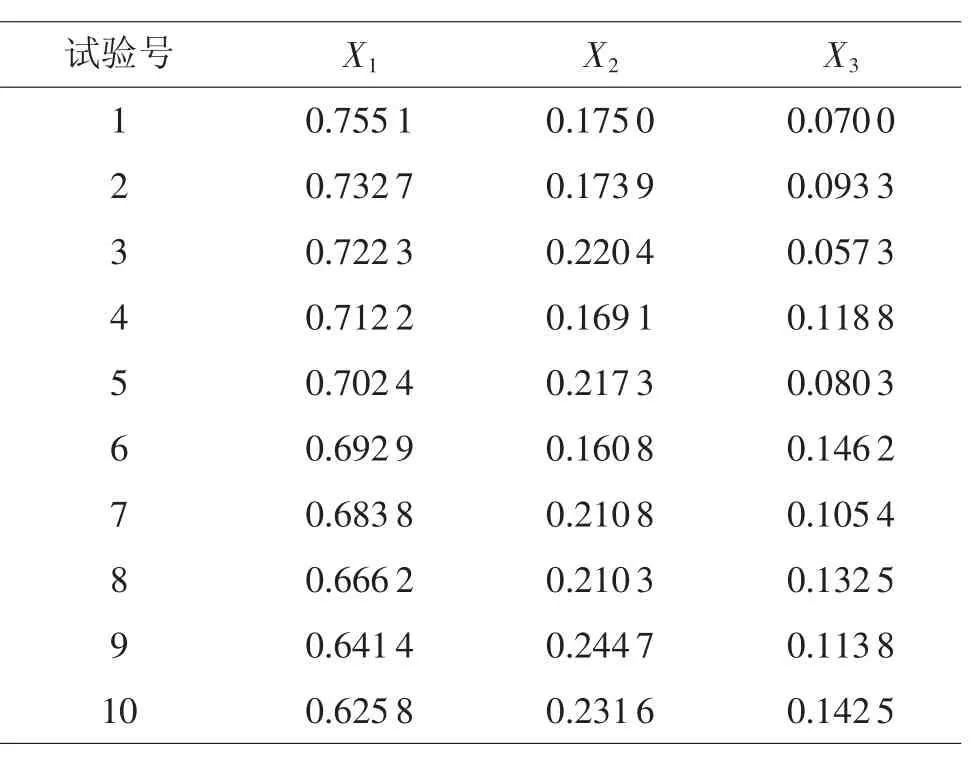
表1 试验方案
上述过程事先难以确定方案的样本量,如果我们要求n=12,就要试算U24*(249)等均匀表;其次变换、判别区域D内的点集计算烦琐,好在中国均匀设计学会有推荐的软件包予以支持。
三、有上、下限约束的混料均匀设计——DPS独特方法
这段时间罗勇推荐段敏伟跟我合作,结合微乳化甲醇柴油的项目及新购置的DPS软件,应用有上、下限约束的混料均匀设计,取得初步成效。由此我们对DPS相关模块作进一步解读。
唐启义著《DPS数据处理系统——实验设计、统计分析及数据挖掘》一书中,专门介绍了“混料试验设计与分析”。在“基于均匀设计表的混料试验设计”中其变换思想、公式以及从Un(nl)变换成UMn(np)的结果和方开泰提出的方法是一致的,对此我们还作了计算核实,见《上海化工》2018年第4期。
(1)在“有上下限条件约束的混料实验设计”中,唐启义把极端顶点设计方法设计点都在边界上这一特点,和方开泰、王元等提出的混料均匀设计方法设计点在区域内均匀布点相结合,采用新的定向优化算法,形成独特的试验设计方法。设置离心(力)系数α=0~1,α=0可得相当于本文介绍的混料均匀设计方案;α=1实验点向区域边界移动,可得极端顶点混料设计方案,同时给出中心点的Xi值,以提高实验效率(相当于《上海化工》2018年第1期中极端顶点中心增强设计方案)。
我们认为DPS把两种算法结合的方法是比较合理的,值得推荐,一般情况取α=0.5。当TP(a,b)考察区域较大时,α取值小时,试验点空间边界和约束空间边界之间有一“空白”地带,如果实验点较多,可适当提高α值以减少空白带,有利于优化精度。
(2)关于试验设计方案实验样本量的选择
经典的极端顶点设计,上下限约束构成凸几何体的约束交点——极端顶点,再取阶数d增强,中心增强,轴增强,见《上海化工》2018年第1期P=3,方案样本量n=16。DPS混料均匀设计建议N=(3~5)P。笔者认为有上下限约束而又不能形成正单形,空间凸几何体比较复杂,样本量n偏上限;对能形成正单形的混料均匀设计方案,n取值偏下限。
(3)DPS混料试验结果统计分析上的独特方法
①混料试验统计分析的数学模型
由于混料约束∑Xi=1,所以用于独立变量的二次多项式或模型不能直接采用,会引起信息矩阵退化,需进行转换,详见《上海化工》2018年第1期。
当P=3时,一般的三元二次回归模型为:
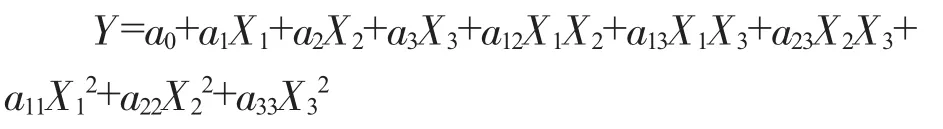
由于X1+X2+X3=1,可转换成有名的也常用的Scheffe多项式:
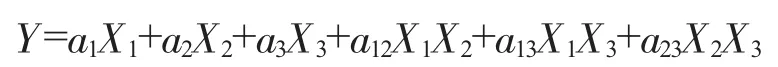
由于X3=1-X1-X2,继续变换,可转换为:
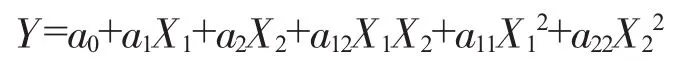
该模型在混料回归分析时可以采用,即去掉一个组分P-1=3-1=2,转换成二元二次混料回归分析。
②DPS系统中进行Scheffe多项式模型分析
将实验方案表和结果一起定义成数据矩阵,执行“试验统计”下的混料试验设计中的“混料回归分析”功能。模块在执行逐步回归过程时,为了保证主组分Xi的完整性,不管P值大小一律进入模型,而且以后也不能剔除。在此基础上,对Scheffe多项式其他变量项进行逐步回归,形成独特算法。
早期混料回归分析采用全回归分析,Scheffe多项式全都进入统计模型,一些不显著项也影响模型的稳定性;后来采用逐步回归剔除不显著项,有可能剔除主成分Xi项,影响模型中配方组分的完整性。DPS该功能模块的算法兼顾统计模型组分的完整性和模型的稳定性,有其合理性。
③DPS系统中进行一般二次多项式模型分析
由于混料试验∑Xi=1,组分之间相互关联,采用一般的回归分析会引起信息矩阵退化,所以采用去掉其中一个组分(P-1)后进行回归分析。但DPS处理混料试验数据,进行二次多项式逐步回归,已在软件计算技术作相应处理,不需要去掉某个组分。
直接将实验方案表和结果一起定义成数据矩阵,用“多元分析”下的回归分析中的“二次多项式逐步回归”功能进行分析,模块执行过程和独立变量的二次多项式逐步回归相同。关键在模型优化界面,见图2。对于独立变量回归分析不点击配方限制,统计模型最优指标各个因素组合预报可用偏导数为零的求极值方法解得。
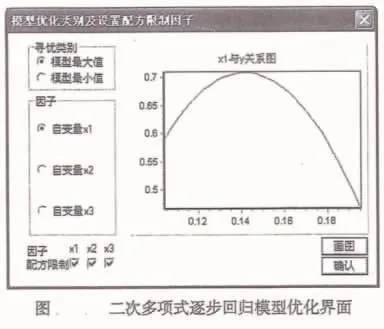
图2 二次多项逐步回归模型优化界面
对于混料回归分析,必须点击配方限制,此时软件自动调取∑Xi=1约束下的优化计算模块,预报最优指标,各个Xi因素,一定满足∑Xi=1。
DPS系统二次多项式逐步回归对混料回归分析的应用,其合理性是明显的。用(P-1)去掉一个组分来统计建模,那么去掉哪个组分呢?是去掉含量高的组分,还是去掉变化范围小的组分?组分选取带有人为的色彩。而DPS系统的处理过程为:那些多项式变量项进入、剔除,统计模型由逐步回归执行过程的方差分析来完成。
此外,当混料试验含有过程变量,不能用经典的Scheffe多项式建立统计模型时,可以应用本算法得到混料组合模型。
四、应用案例
1 实验设计
在前期探索实验的基础上,微乳化甲醇柴油研究在本实验中最终选定油酸、正癸醇、正辛醇等较好的助溶剂进行混料设计,在设计前,先确立各组分的上下限,并将其输入DPS数据处理软件界面中,其数据格式为:一行一个因子,一行中放该因子实验限制条件的下限和上限,实施时将下限、上限数据选中,见图3。
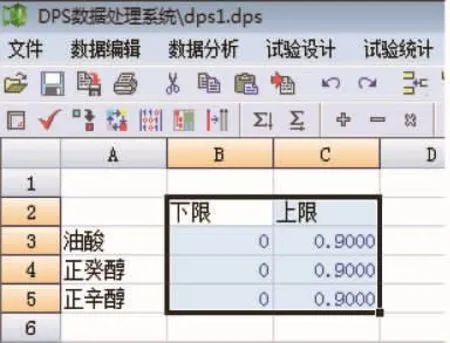
图3 输入各组分及上下限
注意:还要满足的约束条件∑Xi=1。
数据编辑、选中后,在DPS系统下执行“试验设计”菜单下面的“混料试验设计”中的“上下限约束的混料设计”功能模块,操作示意图见图4。系统会显示如图5所示的用户参数界面。在第一个对话框中输入需要的实验次数。第二、第三个对话框是优化过程的精度和时间控制,如在给定精度(0.0001)下能终止迭代过程,系统则根据第二、第三个对话框提供的参数,只要满足一项就终止迭代计算过程,给出实验设计结果。第四个对话框的“离心系数”是DPS作者精心设置的,它是控制实验点从均匀分布(即高维球体内)向极角点(高维球体外)均匀扩散的“离心力”指标,它可以由用户控制实验区域的分布特性。需要说明的是,DPS系统默认的是0.5,用户可根据需要自行修改。
点击“确定”按钮后,生成混料设计方案表,如图6所示。
显然,软件自动进行计算、判断,本案例TP(a,b)非空,在计算、解除多余约束后,给出上述混料试验方案。
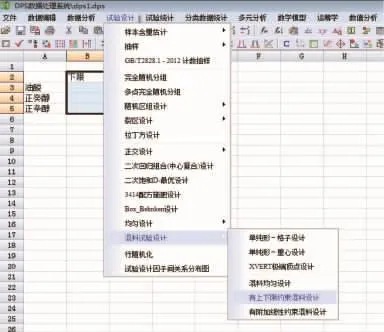
图4 含上下限约束的混料试验设计用户界面
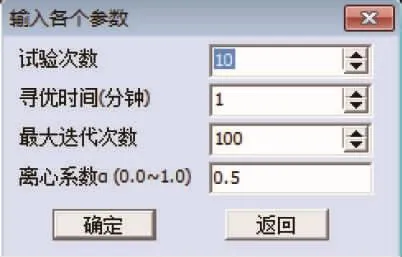
图5 用户参数界面
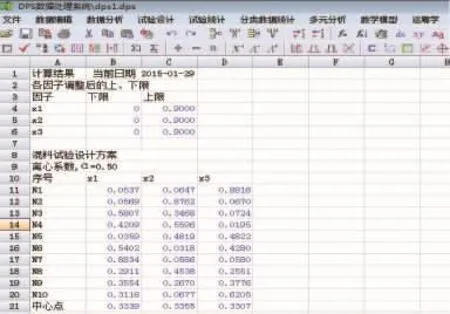
图6 含上下限约束的混料试验方案表
2 实验结果处理
根据生成的均匀表安排实验,获得了各水平的实验结果。将实验方案与实验结果输出至DPS软件界面,实施时将数据选中,见图7。
然后执行“试验统计”菜单下“混料试验统计分析”中的“混料回归分析”功能,操作示意图由图8所示。这时系统弹出如图9所示的参数设置对话框。
如图9所示:实验目标是求极小值;阶次一般取“2”,如果拟合效果不好,可试用Scheffe 3阶模型;同时,实施逐步回归筛选因子。将相关参数设置好之后,点击确定按钮,系统首先将各个分量引入,然后进行逐步回归(引入或剔除变量)。在当前的置信水平分析结束时,系统会出现如下界面,由图10所示,并询问用户是否继续引入变量、剔除变量还是结束变量的引入、剔除工作。
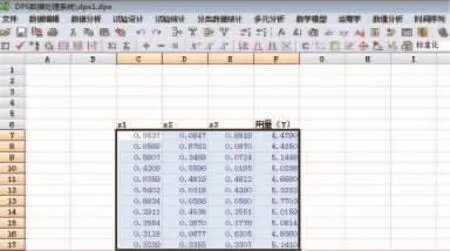
图7 输入实验表及实验结果
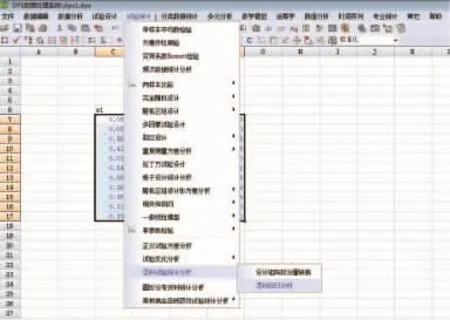
图8 混料回归分析操作步骤
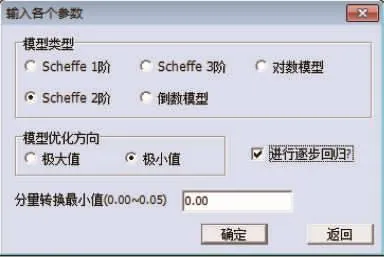
图9 参数设置对话框
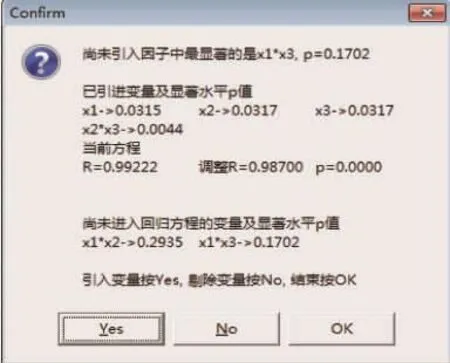
图10 当前的置信水平下变量引入剔除界面
观察P值,由于方程P=0.000 0,已无法继续优化,因此点击OK。软件计算得到的优化结果由图11所示。
从图11的输出结果可以看出,方差分析表中P值等于0.000 1(P<0.01),说明模型有意义,可进一步分析。
但由于各项变量Xi的P值都为0,说明各组分的作用显著。
从输出结果还可以知道本例模型优化得到的助溶剂用量为最低指标时各因素的组合,即当∑Xi=1,X1=0.03567,X2=0.8762,X3=0.0871 时,有预测极小值Y=4.4290。
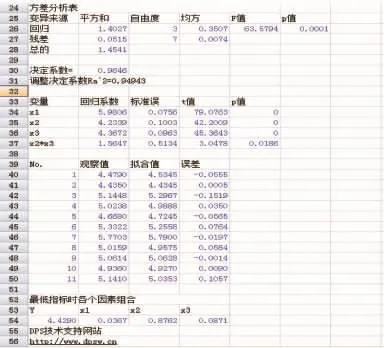
图11 均匀设计计算结果
在最优点处进行补充实验,得到的验证值为4.576 8,与预测值的相对偏差为3.23%,误差较小,说明模型预测准确。
连接中欧成型技术——伊之密开启CHINAPLAS 2018技术创新盛宴
在CHINAPLAS 2018展会上,伊之密沿用“连接中欧成型技术”的参展主题并衍生出更多的创新与融合,如FoamPro微发泡+Deco-Pro表面装饰、MultiPro多物料成型、OpticPro光学产品成型、PacPro薄壁包装产品成型技术等,这些新工艺技术在展会上是首次亮相。
自2016年全球注塑机行业顶尖专家韦伯博士加盟伊之密并出任首席战略官以来,伊之密以更加开放的视野、积极的心态拥抱欧洲先进技术,对接欧洲研发机构、合作伙伴,如IKV(德国亚琛工业大学塑料加工研究院)、AZL(亚琛工业大学轻量化设计中心)。
韦伯博士介绍:“伊之密正努力寻求转型,从过去关注单一的机器业务转而聚焦制品、模具、机器、周边设备及自动化、生产环境等整个生态系统,致力成为技术领先的最佳性价比方案提供商。”为实现该战略目标,未来伊之密将加强与技术合作伙伴、高校研究机构的连接、融合,以及建立伊之密全球开放创新中心,通过德国技术预研引进欧洲即将或已市场化的工艺,在中国落地、工业化.
如今伊之密已在德国注册成立研发中心,并在比利时奥伊彭与Prince&Weiss公司一起投资设立环保塑料创新中心,以此连接高科技研究网络和先进成型技术研发。
当下,汽车轻量化已成为世界汽车发展的必然趋势。伊之密以注塑技术的角度,深入思考如何加速推动汽车轻量化、助力汽车行业的转型与升级。展会现场,伊之密应用最新FoamPro+DecoPro技术展示高端汽车发动机盖的生产流程,通过将背注塑贴膜和微发泡工艺结合,一次成型良好的发泡表面及铝箔装饰。该组合工艺可应用于汽车装饰功能件升级换代,满足金属、皮革、木皮等多种材质的装饰需求,可为产品成型带来减重30%,缩短成型周期15%以上,同时具有能够消除翘曲、缩水,降低成本等多重优点。
值得一提的是,此次Foam-Pro+DecoPro的展示由伊之密联合德国 GK Concept、意大利 HRS-flow、德国SINGLE、德国AKROMID、荷兰LyondellBasell等多家全球合作伙伴共同完成,再次体现了伊之密“连接中欧技术”的决心与诚意。
相比于机器,客户更加关注解决方案。基于此,伊之密从客户应用层面出发,将目光瞄向多物料、液态硅胶等需求较大的领域。MultiPro多物料成型工艺搭载新设备+C系列高端多物料成型注塑机在展会现场生产400 mL大容量双色杯,满足市场个性化需求;OpticPro光学产品成型聚焦液态硅胶材料,现场生产液态硅胶路灯透镜,由伊之密与欧洲合作伙伴共同设计的FF飞凡系列电动注塑机完成,并实现全自动取出、装箱打包全套工序;PacPro薄壁包装产品成型技术专注效率的提升,为客户提供高性价比的解决方案。

