增量理论下J积分路径无关性的数值检验

曾天奇

重庆交通大学 重庆 400074

正文：

在增量理论下J积分与积分路径是否相关是一个很有意义且困难的问题：首先在于数学上的高度非线性性质，一方面，在裂纹顶端的高应力塑性区中，应变的数量具有1的量级，不能再当作微量，因而使问题变为几何非线性的有限变形问题。另一方面，在裂纹失稳扩展前，常常存在着一个稳定扩展阶段，裂纹稳定扩展的尺寸可与起裂前的塑性区尺寸相比拟。在断裂的这一阶段中，裂纹顶端地区不断撕裂，造成该地区应力、应变场的强烈扰动，一部分塑性区发生卸载，以后又重新加载。因而常变量强烈地依赖于应力历史，全量理论已不适用，而必须采用增量形式的本构方程来描述材料。将这样的增量方程与原有的基本微分方程相耦合，构成一组非线性方程。在很难求出解析解的情况下，采用增量有限元数值法作出这一问题的一些数值试验。

1 基本的增量方程和本构关系

考虑直交坐标系，且设ai、xi分别为参考态和现实态中的质点

坐标，vi为速度分量，又变形速度张量为

旋转速度张量为

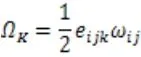
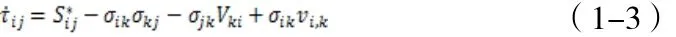
其中“ ”表示物质时间导数。一般有

采用如下的速率平衡方程，即

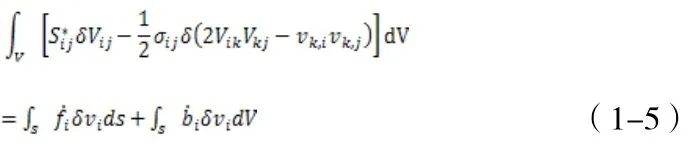
下面构作Euler格式的有限元法基本方程。首先，在现时态构形上划分元素，设为节点速度，各表示元素中一点的速度分量和变形速率。一般有

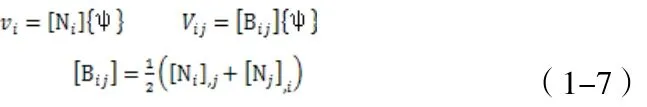
可得下列的增量有限元法方程

其中

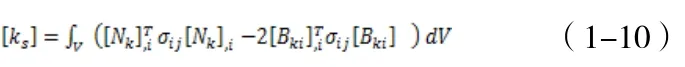
节点荷载速率为

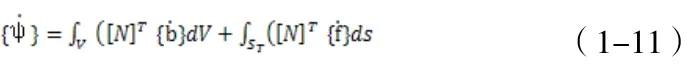
或写为

在具体计算中，仅考虑与应变速率无关的各向同性硬化Prandtl-Reuss材料，此时速率本构矩阵仅与材料特性及应力状态有关。适用于有限变形的由下面的式子决定：对于塑性加载有：

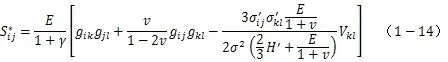
对于弹性加载或塑性卸载，则为

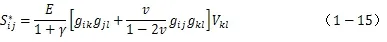
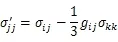
应力状态的判定要计及应力历程的影响，且依据Von-Mises屈服准则

2 计算模型和数值结果

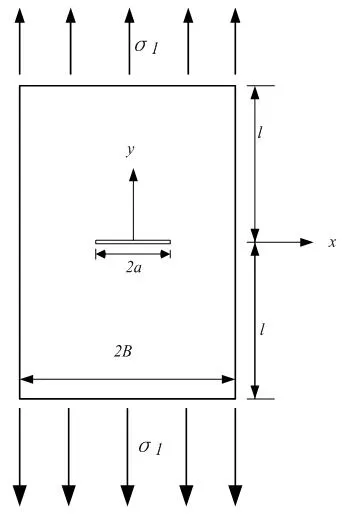
图1

在计算中，采用初应力迭代法，必要时辅以加速收敛的方法。为了考核计算方法和程序，计算如图1所示的中心裂纹薄板。因结构对称，故只需要计算其结构。考虑到使用的是等应力三角形元素，在裂纹顶端附近，元素的线性尺寸取得较小，约为初始裂纹长度的。材料参数选取为

表1 最大等效应力随外荷载的变化

表1 最大等效应力随外荷载的变化

首先进行J进发，裂纹嘴张开唯一COD及线弹性下裂纹扩展力的计算，以便比较验证。计算时采用下列公式，即

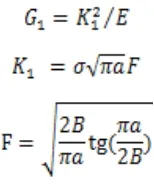
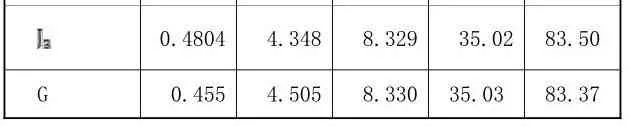
计算结果见表2

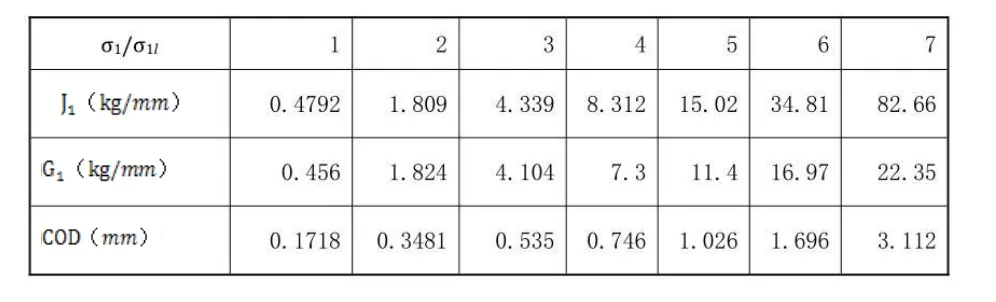
表2 J ，COD和G1的计算值（n=10）

接着对不同的n，选取三条完全任选的路径，有的完全在塑性区，有的部分在塑性区，有的在弹性区中，记为Γ1、Γ2、Γ3。计算后得到表3、表4、表5。其中Ji是对应于Γi的值。

表3 J的计算值，n=10

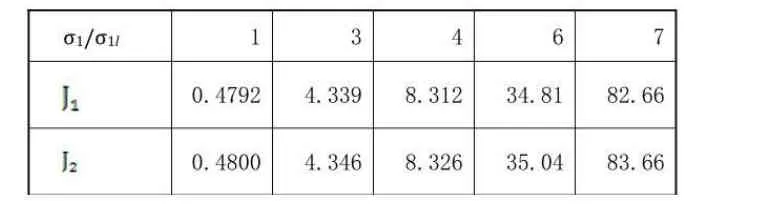
表3 J的计算值，n=10

?

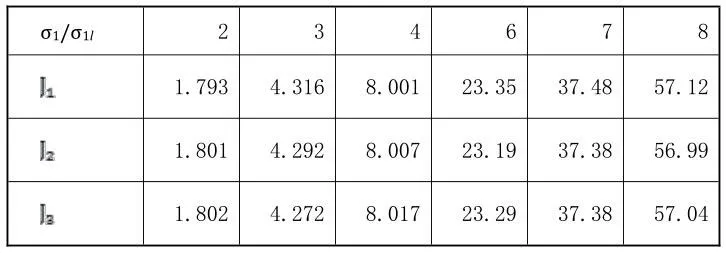
表4 J的计算值 ，n=2

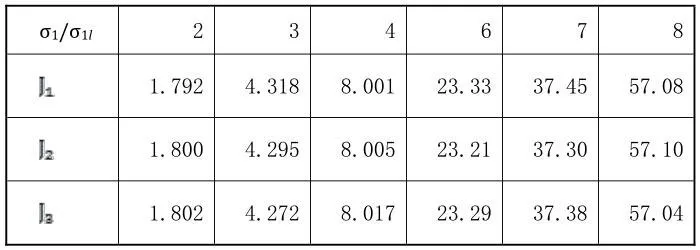
表5 J的计算值 ，n=3

从以上表格可以看见，直到大范围屈服，J关于各种不同的路径具有非常接近的计算值。

3 结论

关于静裂纹的情况所做上述数值试验的结果表明J积分值对路径的相关性是难以察觉的。可以得出，在增量理论下J积分与积分路径无关。