倾斜变截面管理想流体喷射模型的构建
李 轩,李大帅,王俊杰,张冠中,张 雪
(东北师范大学 物理学院,吉林 长春 130024)
理想流体在变截面管中的流动模型可以加深学生对流体动力学和热学等学科的理解程度,增强自身科学素养水平,因此受到了很多竞赛的青睐[1]. 本文把水视为理想流体,首先利用理想气体状态方程和伯努利方程得到最大喷射高度的表达式,建立了倾斜变截面管理想流体喷射模型;引入管径比这一概念,讨论了不同倾角下管内气体温度、初始水量、管径比等参量对最大喷射高度的影响,指出文献[2]分析过程中存在的一些不足并对其进行修正.
1 理论分析
简化模型如图1所示,作以下近似:1)空气视为理想气体,满足理想气体状态方程;2)水视为理想流体且自身特性(如密度等)不受温度等因素的影响;3)短时喷射过程中管内气体温度保持恒定;4)空气阻力、空气流速等对水柱状态不施加影响;5)变截面管内壁光滑且绝热.
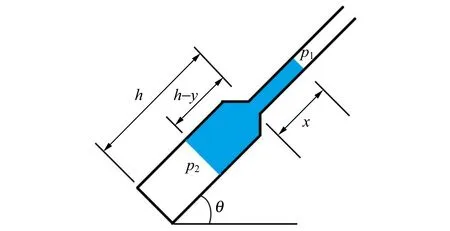
图1 处于喷射过程中的变截面管模型
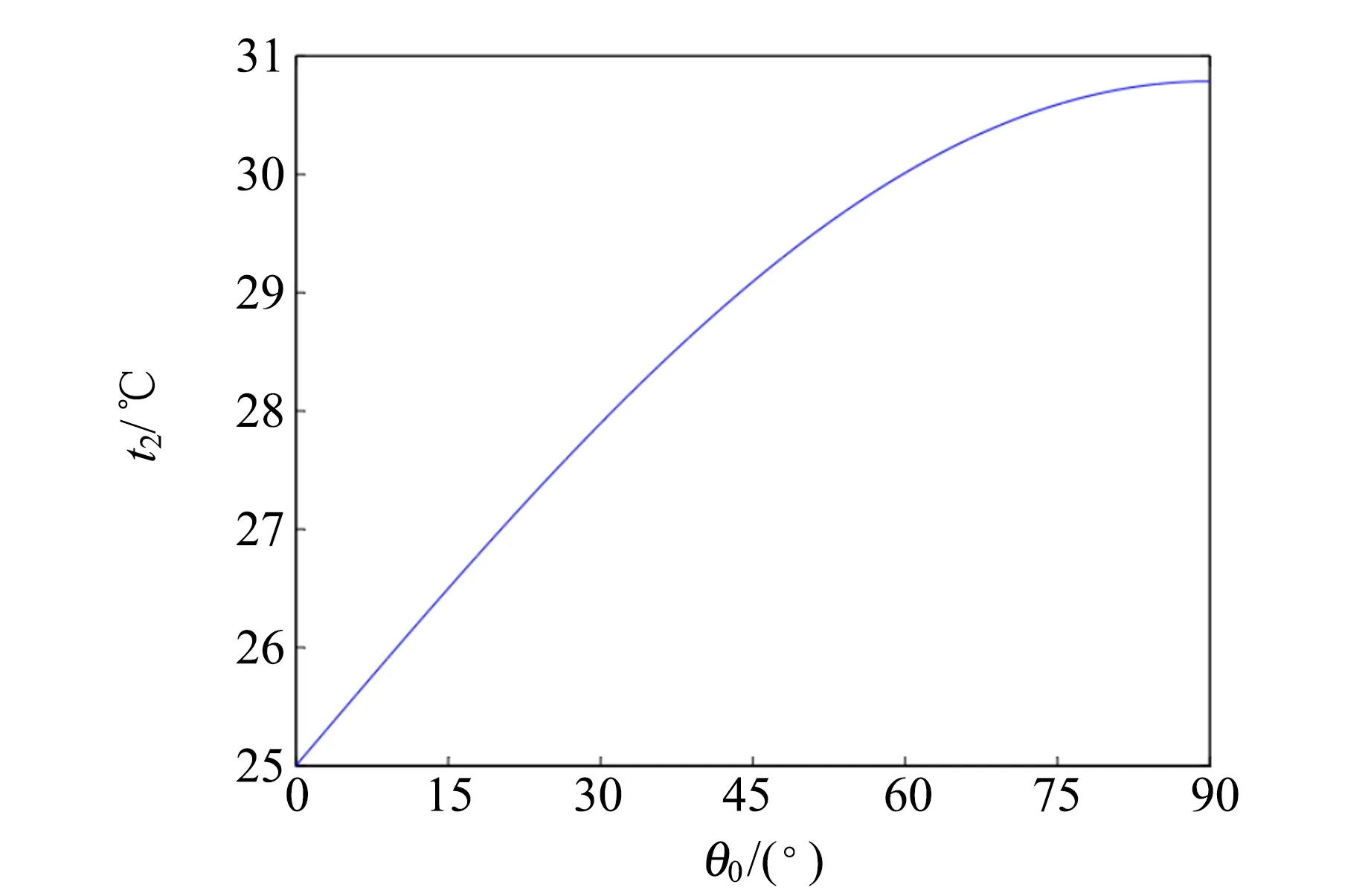
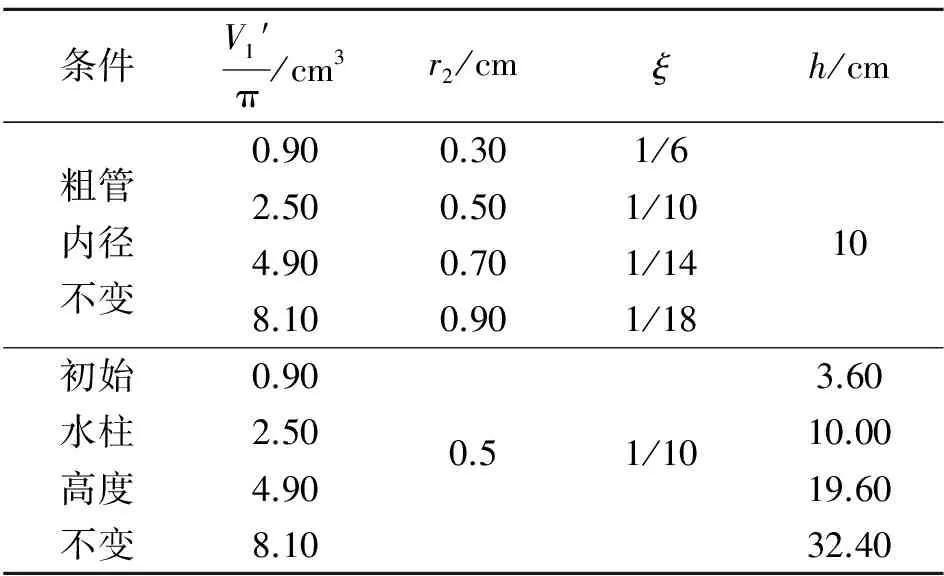
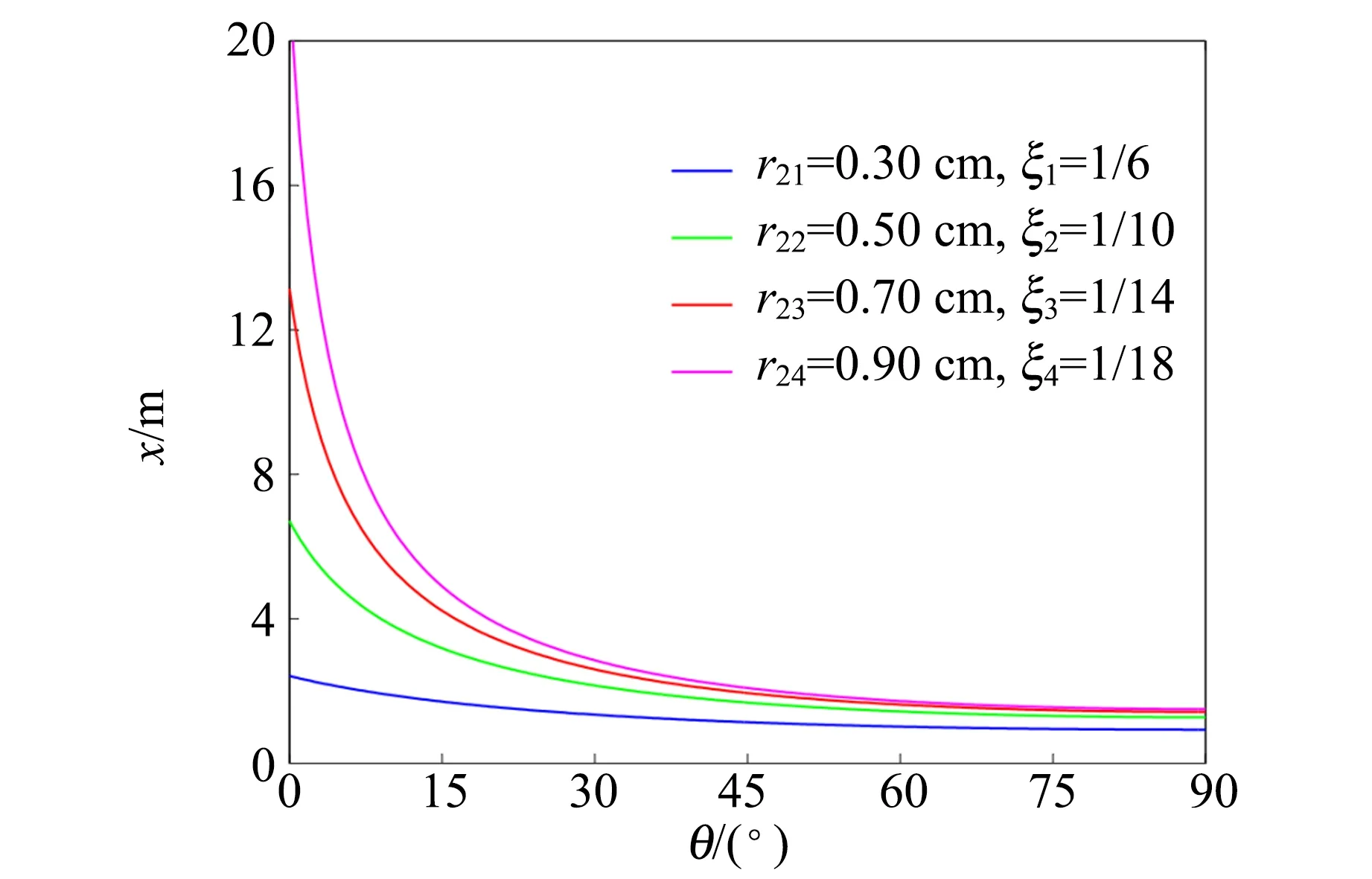
设粗管内径为r2,高度为H,细管内径为r1,室温为T1,大气压强为p1,初始管内的水柱高度为h且h 管内气体变化满足理想气体方程 (1) 对喷射过程列伯努利方程 (2) 并根据流体力学连续性方程,有 (3) (4) (5) 设计参量:管径比ξ=0.1,粗管长H=30 cm,大气压强p1=101 kPa,重力加速度g=9.80 m/s2,密度ρ=1 g/cm3,初始水柱高度h=20 cm,室温t1=25 ℃,气体温度t2=25,50,75,100 ℃.不同倾角下管内气体温度对最大喷射高度的影响如图2所示. 图2 不同倾角下管内气体温度对最大喷射高度 影响关系曲线 由图2可知:1)在气体温度不变的情况下,最大喷射高度x随倾斜角度θ的增大而减小,且减小速率随倾角增大而渐缓. 其原因可以归结为随着倾角的增大,水自身的重力势作为一种阻碍因素对减小喷射高度的促进作用也在随之增大;2)不同倾角θ下,气体温度T2的改变对θ-x关系曲线的影响程度是不同的,倾角越小,温度对其影响程度越大. 这反映出倾角θ和温度T2两参量对最大喷射高度x的作用效果不同,温度的升高对喷射高度的增加起到促进作用,而倾角则恰恰相反;3)当温度t2≤25 ℃时,射流现象不会出现,x值甚至在θ>0°时为负值,即出现了液体倒流现象,且倾角越大,倒流现象越明显. 射流现象主要靠流体下方的空气受热膨胀给流体施以喷射动力形成的,当内部空气一旦丧失了与外界空气存在的温度差之后,热膨胀现象便不再出现,射流现象也不会产生. 如若此时管又具有一定倾角,此时流体便会由于自身受到的重力作用而产生倒流. 而最大喷射高度为0所需满足的条件,可对流体列一平衡方程 p2=p1+ρghsinθ0, (6) 结合(1)式得到 (7) 利用(7)式可以求出在某一特定倾角θ0下流体恰好保持平衡所需的温度,由实验可得t2-θ0图如图3所示. 图3 平衡状态下t2-θ2关系曲线 由图3可知,倾角越大,其所需要保持平衡状态的温度也就越高,并在90°达到最大值,此时流体的重力势能有最大值,与前文所述理论分析一致. 设计参量:细管内径r1=0.50 mm,粗管长H=50 cm,大气压强p1=101 kPa,重力加速度g=9.80 m/s2,密度ρ= 1 g/cm3,室温t1=25 ℃,管内气体温度t2=75 ℃,粗管内径和初始水柱高度h见表1. 图4为不同倾角下初始水量对最大喷射高度的影响关系曲线,由图4(a)可知:1)在管径比固定的情况下,随着倾斜角度的增加,最大喷射高度减小;2)倾角固定时,管径比越小,最大喷射高度越大;3)小角度下的管径比对最大喷射高度的影响是巨大的. 可以看到,ξ1和ξ4仅相差3倍,但在倾角0°时对应的最大喷射高度却差了接近10倍,但管径比在大角度下对最大喷射高度的影响却很小. 图4(b)的曲线形状和图4(a)类似,初始水柱高度同样也是在小角度处对最大喷射高度影响大,但不同的是,倾角固定时,初始水柱高度越大,最大喷射高度越小. 即初始水量增加时,可能会对最大喷射高度造成2种截然相反的结果. 其中文献[1]在研究垂直情况下初始水柱高度对最大高度的影响时,给出了“由于吸水量的增加会导致水柱的质量增加,因此喷泉高度会随吸水的质量增大而减小”这样的解释,从这里看来这种解释是不恰当的,其原因是初始水质量的增加并不一定会造成最大喷射高度的减小. 为此给出较为合理的解释:1)在初始水柱高度保持不变的情况下,管径比越大,管路的收缩程度越大,变截面管对应的粗管口的收缩系数增大,粗管口的流速增大,对应有最大喷射高度增大;2)在管径比保持不变的情况下,增加初始水的高度不仅增加了水的质量,增加了阻力因素,而且减小了热空气体积这一动力因素. 这样从两方面减小了最大喷射高度. 表1 粗管内径和初始水柱高度设计参量 (a)h=10 cm时不同粗管内径下x-θ关系曲线 (b)ξ=1/10时不同初始水柱高度下x-θ关系曲线图4 不同倾角下初始水量对最大喷射高度影响 文献[2]中以吸量管这一变截面管为例对倾角90°时的最大喷水高度影响因素进行了分析,但遗憾的是并未意识到在其他条件不变时,对最大喷水高度起影响作用的因素是管径比ξ. 倾角θ=90°时管径比ξ对最大喷水高度x的影响如图5所示. 设计参量:管长H=30 cm,大气压强p1=101 kPa,重力加速度g=9.80 m/s2,密度ρ=1 g/cm3,初始水柱高度h=20 cm,室温t1=25 ℃,气体温度t2=25,50,75,100 ℃. 图5 垂直状态下管径比对最大喷射高度的 影响 由图5可知,在温度不变时,增加管径比可以增大最大喷射高度,但随着管径比的增大,最大喷射高度会趋于稳定,即管径比对最大喷射高度的影响会随着管径比的增大而趋近于0. 同时应当看到,在t2=25 ℃时,流体确实会因重力势作用发生倒流现象. 结果和上述分析结论自洽,再一次说明了上文分析结果的正确性. 建设了倾斜变截面管理想流体喷射模型,并采用数值模拟的方法研究不同倾角参量的改变对最大喷射高度的影响. 分析得到:1)升高温度、减小倾角、增大管径比、减少初始水柱高度等方法均可使最大喷射高度增加;2)不同倾角下存在不同的特定温度对应流体的平衡状态;3)管径比在喷射模型构建中具有重要作用,对最大喷射高度的影响会随着管径比的增大而趋于0. 参考文献: [1] Ilya Martchenko, Matej Badin, Reza Montazeri Namin,et al.Preparation to the Young Physicists’ Tournaments’ 2016 [EB/OL]. http://iypt.org/Sponsors. [2] 刘建晓,郑永春,史宫会,等. 热水喷泉现象的理论研究[J]. 物理实验,2016,36(4):23-26. [3] Майер В,Мамаева Е. Два физических фокуса // Опыты в домашней лаборатории:Библиотечка Квант, вып.4.-М.: Наука,1981:42-43. [4] 邵超. 射流碎裂理论与实验的对比研究[D]. 西安:长安大学,2015. [5] 娄彦敏,刘娟红,周晓平,等. 温度对水的粘度和扩散系数影响的研究[J]. 西南师范大学学报(自然科学版),2009,34(6):34-39. [6] 李复. 可压缩流体的伯努利方程[J]. 大学物理,2008,27(8):15-18. [7] 漆安慎,杜婵英. 力学[M]. 3版.北京:高等教育出版社,1986. [8] 马增威,汪志勇,韦建卫,等. 大学物理中流体力学问题的计算机模拟研究[J]. 大学物理,2016,35(10):17-19,34. [9] 周丰群. 对可压缩流体若干问题的讨论[J]. 大学物理,1999,18(10):26-29. [10] 张也影. 流体力学[M]. 2版. 北京:高等教育出版社,1986. [11] 张宪瑞,耿天奇,毕荣山. 气液喷射器中不同粒径分布函数下液滴轨迹数值模拟[J]. 青岛科技大学学报(自然科学版),2014,35(1):43-47. [12] 赵朝林. 流体流动中的压强降落[J]. 大学物理,1996,15(4):19-21,37. [13] 郑永令. 流体流动状态与伯努利方程[J]. 大学物理,1994,13(8):1-4.2 模拟研究
2.1 不同倾角θ下管内气体温度T2对最大喷射高度x的影响

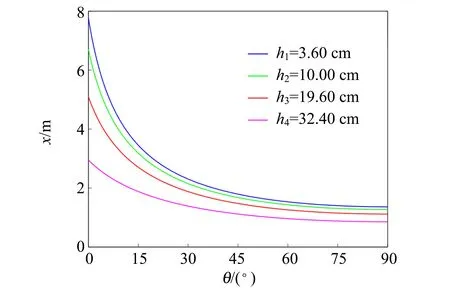
2.2 不同倾角θ下初始管内水量V1′对最大喷水高度x的影响
2.3 垂直状态下管径比ξ对最大喷水高度x的影响
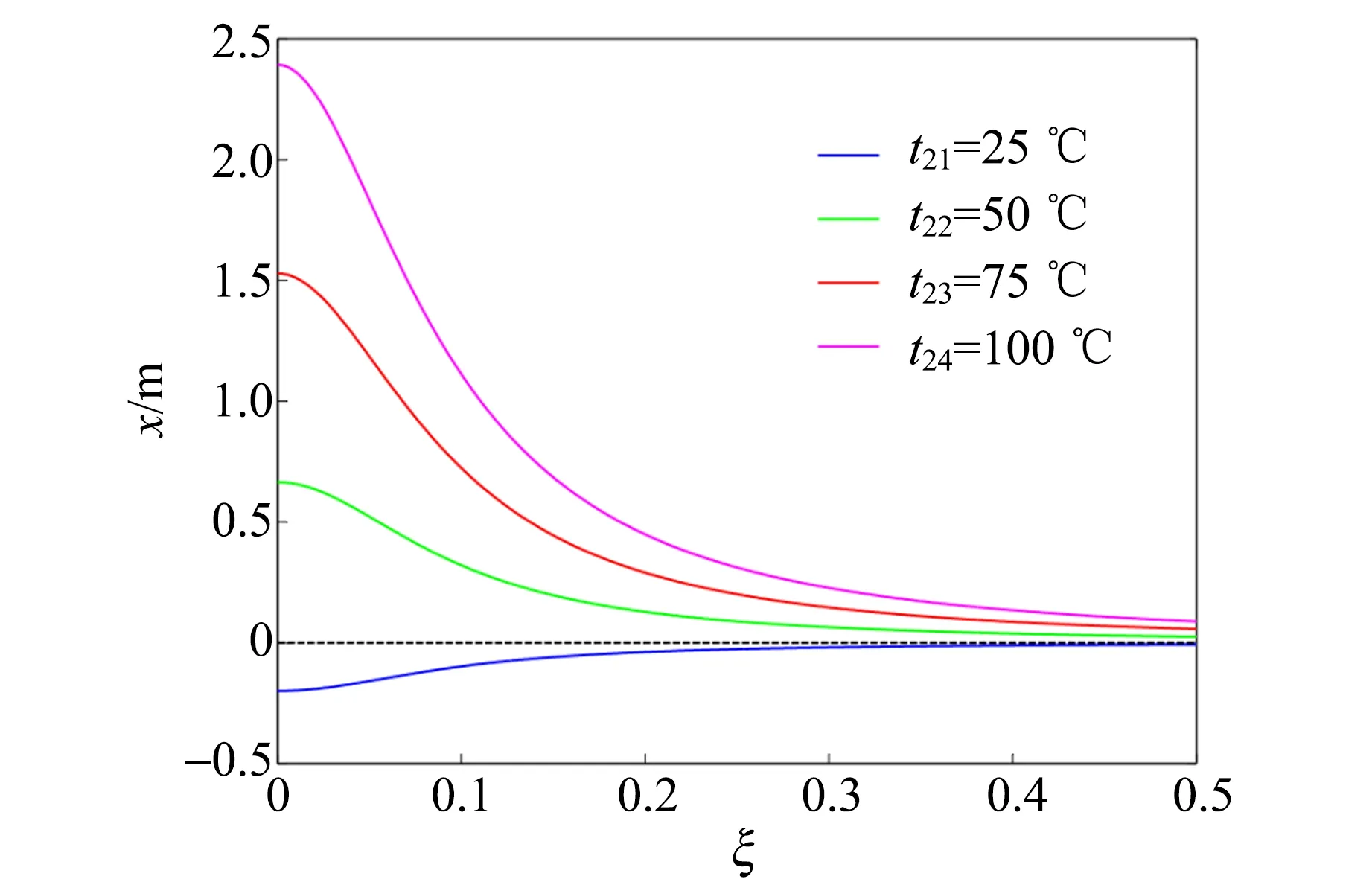
3 结 论

