基于Azure机器学习平台的大学校园用电分析与预测
熊 甜 郑 松 徐哲壮 谢仁栩 葛永乐
(福州大学电气工程与自动化学院,福州 350108)
用电问题一直是电力企业面临的难题,例如窃电问题不仅损害了供电企业的合法权益,扰乱了正常的供用电秩序,而且给安全用电带来了威胁[1]。用电浪费现象普遍存在于工作和生活中,造成巨大能源损耗的同时,影响了我国经济可持续发展的能力。因此,在满足用户正常的用电需求,创建节约友好型社会的背景下,如何利用大数据实现用电量的分析和预测具有重要意义。
近年来,国内外高校纷纷开始建立校园能耗监测平台,用以监督校园用电情况,以此达到节能减排的目的[2]。另一方面,能耗监测平台也为校园用电量的预测提供了数据支撑,而用电量预测正是智能电网中的需求响应和调度的重要环节[3-6]。
本文基于福州大学校园能耗监测平台提供的历史用电数据,通过机器学习方法[7-8]对于福州大学的用电情况进行分析和预测。本文基于Azure机器学习平台[9-10]快速构建了用电数据的分析平台,并根据评估数据和实验计算结果,得出影响用电量的主要因素为最高最低气温以及工作日程安排。根据影响因素的分析结果,本文进一步提出了基于用电突变气温的分段式预测方法:将用电量数据根据用电当日最高气温进行分类,进而基于用电突变气温将用电量数据划分为两段分别进行训练和预测。实际预测结果表明,基于用电突变气温的分段式预测方法能够有效降低预测误差,且其预测精度已经能够满足大多数应用的需求,能够为学校相关部门以及电网配电部门提供有效的参考[11-12]。
下文分别从数据源、基于Azure机器学习平台的数据分析方法、校园用电影响因素分析、校园用电预测等环节对于研究工作进行详细描述。
1 用电数据说明
本文分析所用数据主要有以下两个来源:
1)天气数据。通过福建省福州市闽侯县(福州大学校园所在地)气象局采集 2016年 4月 1日至2017年3月31日时间段内最高温度和最低温度的数据。
2)历史用电量数据。通过福州大学校园节能监管平台(见图 1)导出对校园内每栋楼的能耗统计数据。综合考虑不同人群和楼宇的用电特点,本文选取了福州大学学生公寓2号楼(本科男生)、5号楼(本科女生)、36号楼(研究生)和西三教学楼的用电数据进行分析。时间跨度为2016年4月1日至2017年3月31日,用电量数据精度为每天。
图1 福州大学校园节能监管平台
本文在Azure ML机器学习平台上分析4组数据,每组数据源为一个4×365的矩阵,其中列特征量分别是日期、日最高温度、日最低温度、日用电量4个变量。行特征量代表样本点,表示当前日期下的最高温、最低温和用电量的特征值。
2 基于Azure机器学习平台的数据分析
本文采用微软 Azure机器学习平台(microsoft azure machine learning studio, Azure ML)对用电数据进行分析。Azure ML是一种面向机器学习与大数据分析的云服务平台[13](Platform-as-a- Service,PaaS),能够有效提升采用机器学习方法进行数据分析的效率。该平台的优势[14]主要有:能够在单个实验中一次性尝试多种模型并比较结果,有助于找到最适合的解决方案。在同一个试验中建立多算法模型,对预测结果进行对比分析,通过选择合适的学习算法和海量数据的训练,从而达到建立预测模型的目的。
基于Azure ML的数据分析流程如图2所示,主要由导入数据、数预处理、定义特征、训练模型和模型评价5个基本步骤组成。下文将结合本文所讨论的用电量数据进行介绍。

图2 基于Azure ML平台的用电量预测流程图
2.1 导入数据
在进入Azure ML平台并选择新建试验后,可以采用两种方式将数据导入到试验中:①手动导入到试验中;②通过Reader模块在线与其他数据库匹配读取。福州大学校园节能监管平台并未提供开放的数据接口,本文采用手动导入数据的方式,数据格式必须为CSV格式,通过实验中的DATASET选项导入。
2.2 数据预处理
数据预处理主要分为删除缺失值、异常值处理、数据离散化、归一化处理等。在本文所获取的用电量数据中,寒暑假与周末的用电量存在特殊性,同时部分历史用电量存在缺失等问题,会给分析和预测造成影响。针对这个问题,本文采用了Azure ML的数据分割(Split Data)模块,能够根据设置参数自动对数据集的成分进行筛选,清除掉缺失值与异常值。
2.3 定义特征
导入平台的数据集中,包含着各种特征量,如本文研究涉及的特征量有用电量、最低温度、最高温度等。Azure ML通过“select-columns”(选择数据列)模块筛选出预测模型的特征变量,并传递到下一步机器学习算法中进行训练与评估。“selectcolumns”模块可以直接对数据特征进行选择,不需要在每次试验结束后,对数据进行重新导入,能够有效地提高工作效率。
2.4 应用机器学习算法
本文研究拟基于天气数据和历史用电量数据构建预测模型,Azure ML针对预测数据提供了大量回归算法,本文在Azure ML中采用不同的回归算法模块对校园用电数据进行试验,选取两种效果最佳的算法进行对比分析,即最小二乘法的线性回归(linear-regression)方法[15],以及增强决策树回归(boosted decision tree regression)方法[16-18],分别对数据进行处理。两者在处理数据结果上的差异将在本文第4节进行讨论。
数据分割(Split Data)模块将筛选后的数据按照默认比值 0.75∶0.25拆分为单独的训练数据集和预测数据集,分别用于模型的训练和测试。经模型训练(Train Model)模块拟合出的预测模型,将导入模型测试(Score Model)模块中,进而输入测试集数据用于评估模型的性能。
2.5 模型性能评估
Azure ML提供了模型评估(Evaluate Model)模块,用于对预测模型进行性能评估,平台自带的评估指标包括:受试者工作特征(ROC)曲线、精度/召回曲线或提升曲线、混淆矩阵、曲线下面积(AUC)的累积值等。同时Azure ML还可以将模型测试(Score Model)模块的测试结果导出,由外部程序进行分析和处理。
3 校园用电影响因素分析
本文首先以福州大学 36号研究生宿舍楼的用电数据集为分析对象,选取当日最高气温、最低气温的天气数据作为影响用电量的主要影响因素。另一方面,根据大学的作息特性,将用电量数据划分为:工作日、周末、寒暑假三类。进而在考虑不同天气数据和不同用电量数据集的情况下,基于第 2节所述的操作步骤,在Azure ML平台中采用增强决策树回归(boosted decision tree regression)算法分别建立预测模型,并对预测精度进行评估,得到的影响因素评估表见表1。
每栋楼的用电量各不相同,本文的性能分析采用均方根误差(RMSE)和平均相对误差(MRE)两个指标同时对于预测结果进行分析,即

式(1)、式(2)中,xi表示历史用电量值,表示用电量预测值,n表示测试集的数据个数。
由表1的结果可以看出,寒暑假的用电量与平时存在较大的差异,是否考虑寒暑假的用电量对于用电预测模型具有很大影响。若不考虑寒暑假的用电量,则可以使预测的均方根误差降低约40%。类似地,周末与工作日的用电模式也存在一定差异。与综合考虑周末和工作日的用电量数据得到的预测模型相比,只考虑工作日用电量的预测模型可以降低10%左右的均方根误差。

表1 用电量影响因素分析表
另一方面,最高气温和最低气温对于用电量预测都存在影响。在只考虑工作日用电量的情况下,综合考虑最高气温和最低气温的影响具有最高的预测精度。除了36号楼之外,对于其他宿舍楼进行了相同的分析,得到了类似的分析结论。由于篇幅限制,本文不再列出详细数据。
根据上述分析结果,本文后续分析将只考虑工作日的用电量数据,并综合考虑最高气温和最低气温的影响。本文后续部分将进一步探讨如何提升用电量的预测精度。
4 用电突变气温分析
基于第3节分析的结果,本文将2号楼、5号楼、36号楼和西三教学楼的全年用电量数据,按照最高气温分组并取平均值,得到相同最高气温下的平均用电量,如图3所示。

图3 相同最高气温下的平均用电量
由图3可以看到,每栋楼的用电量曲线存在一个明显的拐点。这是因为低温区与高温区的用电量存在明显的差异:在低温区,用电设备是计算机、照明、热水器等日常用电设备,用电量随着气温变化的趋势不明显;而在高温区,空调等降温设备开始投入使用,同时用电量与气温存在显著的相关性。
根据以上结果,本文提出采取分段预测的方法会得到更好的用电量预测效果。为了进行分段预测,本文首先给出用电突变气温的计算方法:基于历史用电量数据计算出不同最高温度下的用电量平均值T,随后从低温到高温逐个根据以下公式计算Δ,即
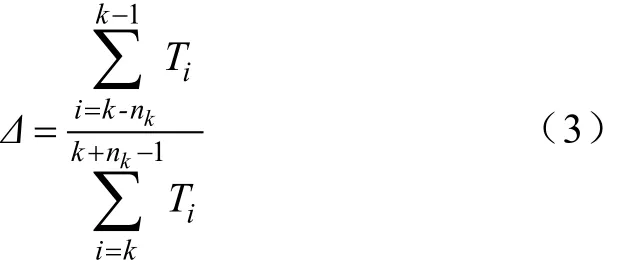
式中,k表示当前最高气温值;nk定义为区间参数,可取为正整数。
给定突变参数阈值θ,若满足Δ<θ,则认定最高气温 k为用电突变气温。nk和θ 为自定义参数,其不同取值将影响用电突变气温选择的结果。根据图3平均用电量曲线图式(3)将分析数据源的nk取1~5之间的整数,θ 取0~1之间的小数,在Azure ML平台上对不同的用电数据源进行测试分析,得到nk=3,θ =0.6时,数据模型的预测预测效果最佳,根据式(3)分别计算出学生公寓2号楼、5号楼、36号楼和西三教学楼的用电数据突变气温见表2。

表2 用电量突变气温
从表2可以看出,用电主体与用电环境之间均存在差异性,使得每栋楼的用电量突变气温也不太一样。福州大学 2号楼为男生宿舍楼,5号楼为女生宿舍楼,36号为研究生宿舍楼,其用电突变气温的差异符合常识中不同性别和年龄对于温度感受的差异。
5 校园用电量预测
基于第4节的分析,本文提出基于用电量突变气温的分段预测方法,并对其预测精度进行分析。用电数据为福州大学2号楼、5号楼、36号楼、西三教学楼。在分段预测方法中,每栋楼的用电数据根据表2提供的用电突变气温划分为“平稳段”和“上升段”两个部分,分段样本点见表 3,采用增强决策树回归算法对两部分数据进行机器学习。在相同条件下,将分段预测结果与传统的整段预测结果进行对比分析,结果见表4。

表3 分段样本点
从表4可以看出,分段预测能够有效降低用电量预测的均方根误差与平均相对误差。相比于整体预测,分段预测能够降低13%~27%的均方根误差,平均相对误差也能够控制在 10.8%以内。以上结果证明了分段预测方法的有效性。
本文中的数据分析主要采用的是增强决策树回归算法。为了证明该算法的有效性,本节将该算法与基于最小二乘法的线性回归算法进行对比。在Azure ML平台中分别采用这两种算法基于福州大学2号楼、5号楼、36号楼、西三教学楼的用电量数据进行了分析和预测,其预测结果的对比见表5。
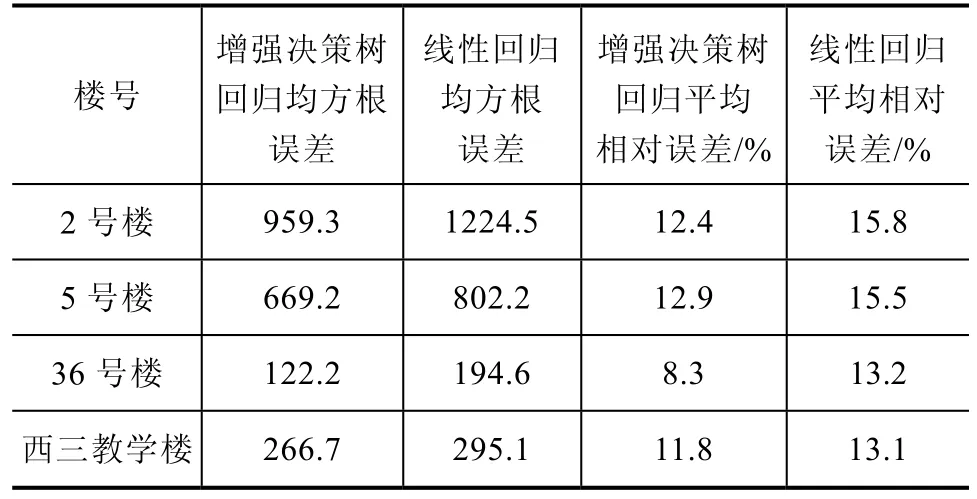
表5 增强决策树回归与线性回归算法预测结果对比
由表5可知,增强决策树回归算法得到的预测模型相比于线性回归算法得到的预测模型,其预测结果的均方根误差要小 9.6%~21.7%,平均相对误差也要减少 1.3%至 4.9%。因此证明了增强决策树回归算法具有更好的预测效果。
6 结论
本文基于用电数据和天气数据,通过Azure机器学习平台对于福州大学校园的用电情况进行了数据分析,总结出了影响用电量的两大因素:气温与工作日程安排。根据分析结果,本文进一步提出了基于用电突变气温的分段式预测方法,并通过测试数据证明了该方法能够有效降低用电量预测的误差。数据分析结果证明,该方法的预测精度已经能够满足大多数应用的需求,能够为学校相关部门以及电网配电部门提供有效的参考。
参考文献
[1] 陈晶晶, 李红娇, 许智. 基于随机森林的用电行为分析[J]. 上海电力学院学报, 2017(4): 331-336.
[2] 王仁祥, 王小曼. 终端用户分布式新能源接入智能配电网技术研究[J]. 电气技术, 2010, 11(8): 58-62.
[3] Stroombergen A, Tait A, Patterson K, et al. The relationship between New Zealand's climate, power,and the economy to 2025[J]. New Zealand Journal of Social Sciences, 2006, 13(1): 139-160.
[4] Wang Zhiyong, Cao Yijia. Mutual information and non-fixed ANNs for daily peak load forecasting[J].Power Sys-temsConference and Expoxision, 2006(5):1523-1528.
[5] 黄海新, 邓丽, 张路. 基于需求响应的实时电价研究综述[J]. 电气技术, 2015, 16(11): 1-6.
[6] 曲朝阳, 张率, 刘洪涛. 基于用电影响因素回归的小区用电预测模型[J]. 东北电力大学学报, 2015(01):73-77.
[7] 张棪, 曹健. 面向大数据分析的决策树算法[J]. 计算机科学, 2016(S1): 374-379, 383.
[8] 王桂玲, 韩燕波, 张仲妹, 等. 基于云计算的流数据集成与服务[J]. 计算机学报, 2017(1): 107-125.
[9] 王永康. Azure云平台对Twitter推文关键字实时大数据分析[J]. 电脑编程技巧与维护, 2015(12): 68-72.
[10] Xiao Laisheng, Wang Zhengxia. Cloud computing: A new business paradigmfor E-learning[C]//International Conference on Measuring Technology and Mechatronics Automation (ICMTMA 2011) 3rd, 2011:Shanghai, China.
[11] 王颖, 赵航宇, 赵洪山. 配电网自动化建设的现状与若干建议[J]. 电工技术, 2015(11): 82-83.
[12] 何春光, 卢志明, 姜春莹, 等. 移动式应急配变的研制[J]. 电工技术, 2016(2): 6-7.
[13] Brandon Butler. 2017年必须关注的10大云趋势[J].计算机世界, 2017(4).
[14] 易植. Windows Azure 新服务, 让机器学习触手可及[J]. 英才, 2014(9).
[15] 韩阳, 吕由, 潘宇航, 等. SVM、BP神经网络、线性回归的比较研究[J]. 河北联合大学学报(自然科学版), 2017, 39(2).
[16] Song Y, Wang H, He X. Adapting deep RankNet for personalized search[C]//ACM International Conference on Web Search and Data Mining, 2014: 83-92.
[17] 柯国霖. 梯度提升决策树(GBDT)并行学习算法研究[D]. 厦门: 厦门大学, 2016.
[18] 王天华. 基于改进的 GBDT算法的乘客出行预测研究[D]. 大连: 大连理工大学, 2016.

