寒冷地区河流冰层结冻后温度场计算研究

孙 凡 李春良 季东航

(吉林建筑大学 交通科学与工程学院,长春 130118)

在寒冷的冬天,北方严寒地区的河流内会形成一定厚度的冰层,对于结冻后的冰层,随着气温的变化,冰层内部温度也随着发生相应地变化[1].冰强度的主要控制因子是冰温度,因此提供冰工程活动科学参数就需要给出冰层内部不同位置处的温度[2-3].用解析法计算温度场是很难求出结果的,因此较多学者在使用各种数值解法解决问题[4].常用的数值解法包括有限元法、有限差分法、变分法等.本文结合冰层特殊的性质,利用差分法求解冰层温度场，将结果与有限元法计算结果进行比较,并对不同条件下的冰层温度场分布规律进行分析.

1 冰层温度场计算模型

1.1 冰层结构的划分

在对冰层进行温度场计算时,因为冰的热学性质随温度的变化而改变,所以将冰层沿厚度方向划分成有限层(见图1).为分析方便确保计算精度较高,将冰层划分为若干层(见图2),并假设第一层上表面的温度T0等于外界的气温,冰层的下表面为冰水交界面,即TK为冰水混合时的温度(0℃),各冰层间的温度是连续的,假设已知初瞬时整个物体上温度的分布,即Tii=0(i=0…K).

图1 冰层结构的分层图Fig.1 Stratification of ice structure

图2 冰层内部温度场划分Fig.2 Division of temperature field inside ice

1.2 冰层温度场模型

根据图2,可能建立冰的热传导微分方程:

(1)

(2)

其中,aT=λT/(CT·ρT)为导温系数,m2/s.参数参考YEN[5]的研究;λT为导热系数,λT=2.22(1-0.004 8×T),W/(m·℃);CT为比热容,CT=2 096.8+7.122×T,J/(kg·℃);ρT为物体密度,ρT=916.8-0.133 4×T,kg/m3;w为单位时间单位体积发出的热量,kcal,因为冰层内部无热源,所以W=0.

任意取出一层r,对空间采用中心差分公式,其中,h为每一层冰的厚度,m.

(3)

对时间变量t的导数应用线性差分公式,将(t0-Δt),t0,(t0+Δt)时刻的温度分别用上标表示为T(t0-Δt),Tt0,T(t0+Δt).

将T(t)在t0点用泰勒公式展开,即:

(4)

略去三阶量,对上式求导得:

(5)

(6)

当t=t0-Δt时,上式中Δt为负值,导出对t0时刻的向后二次差分公式为:

(7)

(8)

将(3)带入上式,整理得差分方程:

(9)

由于此格式是隐式方程,必须进行迭代计算,由上一时刻的温度场作为基础,对此刻每一点的温度整理差分方程,联立每一点的方程求解,即可求得温度场.

2 算例

假设某河流结冰层厚0.5m,为计算精度将其分20层,冰层升温工况分3种,初始温度场分布见图4.

图3 初始温度场分布图Fig.3 The initial temperature field distribution

(1) 假设冰层初始温度按线性分布,其中外界温度为-10℃,气温2h内从-10℃均匀升温到-5℃.

(2) 假设冰层初始温度按线性分布,其中外界温度为-10℃,气温4h内从-10℃均匀升温到-5℃.

(3) 假设冰层初始温度按非线性分布(为工况1的ANSYS求解结果，数据见表1),其中外界温度4h内始终保持-5℃.

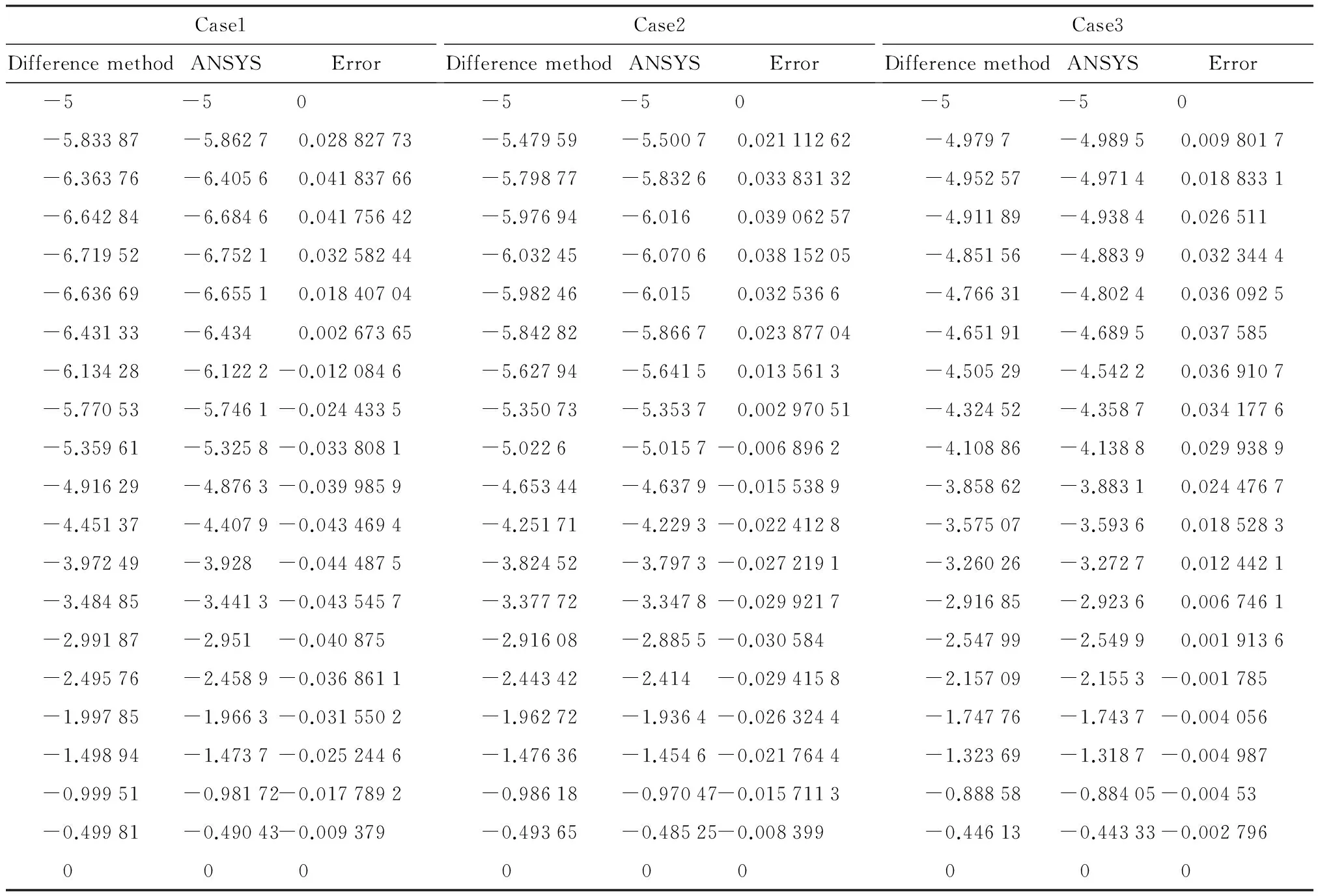
表1 3种工况求解结果及误差

为利用本文公式计算出不同初始温度下,外界温度改变后的冰层内部各点的温度变化分布规律曲线见图4,

图4 变化后温度场分布图Fig.4 The post-change temperature field distribution

3 结果与讨论

观察发现,本文的计算结果与ANSYS计算结果吻合,并具有一定的一致性.

进一步分析可知,随着外界温度的改变,冰层内部温度场也会受外界温度变化而改变，并且温度场分布曲线可以认为由两部分组成,即上部的曲线段和下部的直线段.主要原因是因为冰层靠近顶层,其内部的温度变化很明显,越往下部反应越缓慢.

工况1和工况2在距离上部约0.1m处出现拐点,即最低温度出现在距上端面1/5处,在0.2m～0.5m段和近似认为是直线段.总体而言,在上部呈抛物线形,下部为直线型,温度变化的最大位置在上表层.工况3的最低温度出现在上表面,是因为初始内部温度场和变化时间较长造成的,此时温度变化最大的位置在冰层内部约1/5处.

4 结论

本文利用差分法求解出冰层的温度场,同时对照有限元法的求解结果表明:

(1) 靠近冰层顶部对外界温度变化响应比较敏感,靠近下部的温度场分布趋近于直线.

(2) 经实例分析,有限差分法求解出的冰层温度场结果与有限元法求解结果最大误差绝对值为4.4%,两者吻合较好,具有一定的一致性.

(3) 从冰工程角度出发,冰层温度场的研究是研究冰工程结构受力的必须涉及的问题,可作为后续研究冰层因温度变化膨胀后,对一些冰冻结构的受力分析奠定了基础.

参 考 文 献

[1] 宋涛.静冰荷载对水工建筑物的影响研究[D].天津:天津大学,2007.

[2] Timco GW,Frederking RMW.Compressive strength of sea ice sheets[J].Cold Regions Science & Technology,1990,17(3):227-240.

[3] 于天来,雷俊卿,单思迪.计算春季流冰对桥墩动压力日冰温取值的试验研究[J].中外公路,2010,30(4):220-223.

[4] 铁摩辛柯,古地尔.弹性理论[M].北京:高等教育出版社,1990.

[5] YEN,YC.Review of thermal properties of snow,ice and sea ice[R].CRREL Report, USA Cold Regions Research and Engineering Laboratory,2011.