基于格雷码和多步相移法的双目立体视觉三维测量技术研究
,
(南京理工大学 自动化学院,南京 210094)
0 引言
眼睛在人类的所有感觉器官中最为重要,人们从外界接受的信息绝大部分都来自于我们的眼睛,我们常常通过双眼感受这世界的种种美好[1]。计算机视觉就是模仿人类视觉系统,以各类成像系模仿眼睛,计算机模仿人的大脑进行处理接受到图像信息,其目的之一就是根据获相机取到的图像二维信息转变为目标物的三维坐标[2]。因此,随着科学技术的发展三维测量技术在工业产品模型设计、精密部件测量、医学领域等方面有着重要的研究意义。
本文在基于格雷码和多步相移法的基础上结合双目立体视觉进行三维测量技术研究,第1节介绍了双目立体视觉成像原理和立体校正方法,第2节介绍了格雷码与多步相移法的编解码原理,第3节通过实验论证了基于格雷码和多步相移法的双目立体视觉三维测量技术的可行性。纸盒三维测量实验在完成双目校正的基础上,向物体表面投射7幅格雷码图案和15幅相移编码图案,最后根据相机获取的物体编码图像解码得到物体的三维信息[3]。
1 双目立体视觉
如图1所示,根据是否要接触待测物体,三维测量可以分为非接触式和接触式[4]。非接触式测量中根据是否主动向待测物体投射光源,非接触式三维测量又可以分为被动式和主动式,其中主动式三维测量通过向待测物体投射特殊的光源,形成相应的图像,最后由相机采集图像经过计算机处理,得到物体的三维信息[5]。
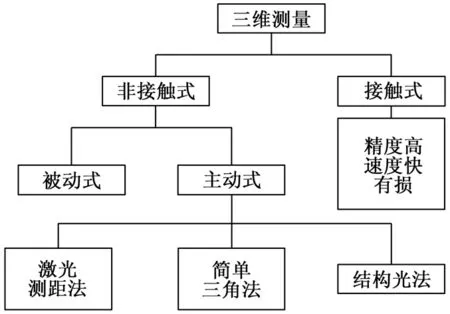
图1 三维测量分类
双目立体视觉属于被动式三维测量方法,由环境中的自然光,如太阳的直射光和天空光对待测物体进行照明,而不需要向待测物体投射人造光源进行照明[6]。双目立体视觉通过模拟人的双眼,将两台相机安装在待测物体的两个不同视角位置,使得两个相机与待测物体构成一个三角形,最后根据对待测物体拍摄得到的两幅图片和三角法原理获取待测物体的三维信息[7]。双目立体视觉虽然不需要向待测物体提供人造光源,成本低廉,但是对没有较多特征的物体图像匹配困难,精度低。
编码结构光法属于主动式三维测量方法,需要向待测物体投射特定的编码图案,然后由相机获取一系列的编码图像解码,进而得到物体表面每条条纹的特定编号以及对应光线投射角,再由结构光基本公式获得待测物体的三维坐标[8]。
1.1 双目相机校正
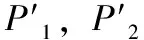

图2 双目视觉系统
首先根据张氏标定法求得左右相机各自的旋转矩阵和平移矩阵。点P和P1,P2点可表示为:
(1)
由式(1)可以得到两个相机之间的相对关系:
P1=R2R1- 1P2+T2-R2R1- 1T1
(2)
由式(2)可以得到两个相机之间的相对旋转矩阵R和平移矩T阵为:
(3)
首先将左右相机成像平面各旋转R的一半,使左右相机的成像平面重投影畸变最小,左右视图共同面积最大[10]。
(4)
此时左右相机的成像平面平行,但是与基线不平行,对此我们需要构造变换矩阵Rrect:
Rrect=[(e1)T(e2)T(e3)T]T
(5)
构造e1使得左视图极点为无穷远处,构造e2与主光轴方向正交,与e1垂直,构造e3与e2和e1正交:
(6)

(7)
1.2 双目相机成像原理
在完成双目校正后,极点e1,e2位于无穷远处,两相机的光轴平行,同一物点的像点在左右相机中高度相同。极线约束使得对应像点的寻找由面搜索变为线搜索,二维搜索变为一维搜索,而经过相机校正后对应点搜索变为同一行搜索,大大减少了计算量[4]。
图2中,根据三角相似关系可以得到:
(8)
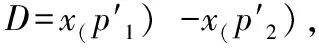
(9)
由此我们可以得到相机图像中点P1与世界坐标系中点P的关系为:
(10)
其中:点cx,cy为左相机主点坐标。根据式(10)可以得到左相机图像坐标系中点在世界坐标系中对应点坐标为(X/W,Y/W,Z/W)[11]。
2 结构光
编码结构光法是一种主动式三维测量方法,由投影仪向待测物体投射一系列编码图案,使得物体具有容易识别的特征点[12]。再由相机获取图像解码获得特征点的投射角度,最后根据三角法求得物体的三维坐标[13]。编码结构光法与点结构光和线结构光结构光相比,测量速度快,时间短,与传统的双目视觉相比具有更高的匹配精度,对于特征不多的图像也能有着很好的测量效果。
2.1 格雷码
在结构光编码中,二进制编码使用最为普遍,其原理也最为简单[14]。投影图像只需要用两种颜色来区分不同的条纹,分别记为0、1,其中0对应黑色,1对应白色。通过向待测物体投射m幅二进制编码图案,将待测物体表面划为个区域。格雷码由二值码发展而来,它与普通二值码相比更加可靠。如表1所示,十进制的1变成2的时候,二进制码的每一位数值都要进行跳变,而格雷码只有一位进行跳变。
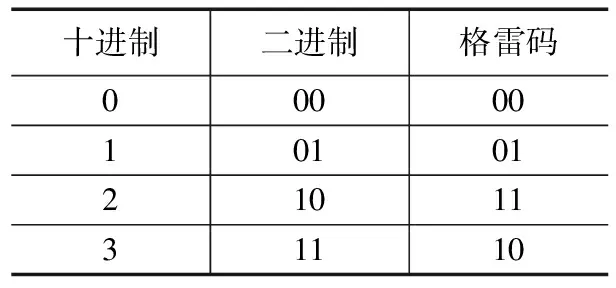
表1 二进制与格雷码比较
格雷码属于可靠性编码,当状态发生变化时只存在一位跳变,而不会出现多位跳变的情况,提高了解码的正确率,可以更加方便检测条纹编码是否出错[15]。格雷码编码原理简单,准确度高,但是在三维测量需要投射大量图案,而且随着图案的增加,黑白条纹边界分辨率降低,降低测量的准确度。因此,我们先向待测物体表面投射如图3所示的7幅格雷码图案,将待测物体表面分为128个区域。格雷码解码后可以获得0~127周期次数k,再向待测物体表面投射多步相移图案来进行三维测量。

图3 格雷码图案
图像阈值分割中无论是采用自适应阈值还是固定阈值都存在不可避免的错误,对此我们采用简化的Daniel Scharsterin[16]方法,在向物体表面投射如图3所示的格雷码图案后,再向物体表面投射如图4所示的格雷码取反图案。(x,y)处投射格雷码图案时灰度值为I(x,y),投射格雷码取反图案时灰度值为I′(x,y),若I(x,y)-I′(x,y)>20则取值为1,反之为0。
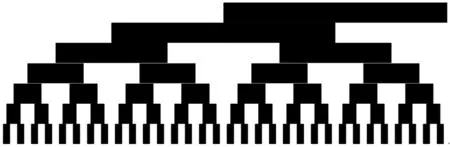
图4 格雷码取反图案
2.2 多步相移法
相移法是按顺序向待测物体表面投射多幅正弦周期相移图案,然后由相机获取经相移图案调制的待测物体图像,解码得到待测物体表面每点的主相位值[17]。向物体表面投射如图5所示相移图案,点(x,y)处光照强度为:
In(x,y)=I′(x,y)+I″(x,y)[cosθ(x,y)+2nπ/N]
(11)
其中:In(x,y)为点(x,y)在第n幅相移图中的灰度值,I′ (x,y)为条纹光的背景光强,I″(x,y)/I′(x,y)为条纹反差,θ(x,y)(θ∈(-π,π))为待求主相位值:
(12)

图5 相移图案
相移法的优点在于每点的相位值不受邻点光照强度的影响,分辨率高,同一周期内每点相位值绝对唯一。缺点在于图像中周期的确定存在二义性,因此我们需要先用格雷码对物体表面进行周期划分,再用相移法对物体表面进一步细分。格雷码图案的最小周期必须为相移图案周期的N倍,以保证在主相位值发生突变时周期值k同步突变[18]。
将点(x,y)出由相移法得到的主相位值θ与格雷码解码周期k向叠加,求得点(x,y)的绝对唯一主相位值ψ(x,y):
ψ(x,y)=2kπ+θ(x,y)
(13)
2.3 周期校正和匹配点搜索
在理想情况下主相位值θ和格雷码解码周期k同步发生突变,求得的每点主相位值ψ(x,y)单调递增,即ψ(x,y+1)>ψ(x,y)。但是考虑到环境光照强度、相移图案稳定性等一系列因素,可能会导致格雷码解码周期k与主相位值θ之间存在着周期错位。若相邻两点之间发生周期错位,则ψ(x,y)-ψ(x,y+1)≈2π。因此我们选取阈值π来判断是否发生周期错位,若ψ(x,y)-ψ(x,y+1)≥π,则令ψ(x,y+1)=ψ(x,y+1)+2π。
由图2可知,在完成双目校正后,点P在左相机中成像位置的横坐标x1必定大于在右相机中成像位置的横坐标x2。而且考虑到在周期校正后主相位值绝对递增,因此点P在右相机中成像平面的对应点可以在(0,x2)采用二分法进行查找。
3 实验结果与分析
为验证基于格雷码和多步相移法的双目立体视觉三维测量方法的可行性,搭建三维测量系统结构。实验器材包括:相机两个(分辨率为1 920×1 080),投影仪一台(分辨率为1 280×800),计算机一台,一张打印棋盘格的A4纸一张和待测物体白色盒子一个。
首先对双目相机进行立体校正,使得左右相机严格遵循行对齐,校正效果如图6所示。

图6 棋盘图像
完成双目相机矫正后向白色盒子表面投射7幅格雷码图案和7幅格雷码取反图案,最后再投射15幅相移编码图案,如图7所示。

图7 格雷码与相移法图像
对获取到的图像进行解码,得到视差图,结合双目视觉成像原理,求出白色盒子的世界坐标系中的三维信息,将点云导入到meshlab中结果如图8所示。

图8 白色盒子点云图像
由图8所示7步格雷码和15步相移法很好的反映了白色盒子的三维形貌,为了进一步确定三维测量的精度,以盒子高度为基础值,求解最大测量误差,并与4步相移法的测量结果作比较,如表二所示。
表2 三维测量比较

测量方法指标项 7步格雷码与15步相移法7步格雷码与4步相移法点云数目/万2118点云距离/mm021024最大误差/mm054082编码图案/幅2918点云计算时间/ms67655413
理想情况下相移和测量不存在误差,则根据4步相移法可以精确计算出物体每点的相位值。但是,在实际应用中测量值受到相移误差、传感器误差和周围环境的影响,导致测量值不精确。采用15步相移法对测量值进行优化统计,虽然无法完全消除误差,却大大降低了误差带来的影响。由表二我们可以看出采用15步相移法与4步相移法相比,虽然需要投射更多的编码图片,解码并计算三维点云的时间更长,但是在测量精度上有着极大的提高,能够更好的体现三维物体的形貌。
4 结束语
三维测量技术在文物保护、自动化生产、精密工业部件测量和逆向工程等方面有着重要的应用,并且随着成像设备、投影仪和其他光电元件的进步,测量的精度也在不断的提高。
本文基于格雷码和多步相移法的双目立体视觉三维测量技术研究,在完成双目相机校正的基础上向待测物体投射格雷码图案和多步相移图案,对得到的编码图像进行解码很好的重构物体的三维形貌。并与4步相移法进行比较,证明投射多步相移图案虽然会牺牲一些测量时间,但是能够获得更加细致物体三维信息,测量精度更高。
参考文献:
[1]陆 乐. 平面设计中的视觉流程概述[J]. 科技创新导报, 2008(33):67-67.
[2]戴 磊. 基于视觉反馈的移动机器人控制[D]. 上海:上海交通大学, 2011.
[3]苑惠娟, 于 佳, 尚爱军. 基于颜色编码的大型物体表面三维测量[J]. 红外与激光工程, 2008(s1):166-169.
[4]喻士领. 基于光栅条纹投影的三维测量系统标定方法的研究[D]. 南京:南京理工大学, 2015.
[5]许志梁. 基于结构光和立体匹配的稠密深度获取技术研究[D]. 上海:上海交通大学, 2009.
[6]许志梁. 基于结构光和立体匹配的稠密深度获取技术研究[D]. 上海:上海交通大学, 2009.
[7]沈国峰. 基于双目立体视觉的牙颌模型测量技术研究[D]. 南京:南京航空航天大学, 2013.
[8]方 勇. 颜色编码三维测量的图像处理方法研究[D]. 哈尔滨:哈尔滨理工大学, 2009.
[9]刘 伟. 基于多视点的三维重建技术研究[D]. 太原:太原科技大学, 2009.
[10]张颖江, 潘 尧, 吴 聪. 基于车载系统双目CCD相机测距[J]. 信息安全与技术, 2016, 7(1):57-62.
[11]钱 真, 彭秀艳, 贾书丽,等. 动平台下双目视觉定位标定算法研究[J]. 计算机仿真, 2012, 29(10):293-297.
[12]雷 震. 单相机单投影仪的编码结构光三维测量方法研究[D]. 武汉:华中科技大学, 2015.
[13]刘 欢. 实时彩色三维建模技术研究[D]. 成都:电子科技大学, 2015.
[14]刘永久. 基于结构光投影的运动物体高速实时三维测量方法研究[D]. 合肥:中国科学技术大学, 2014.
[15]宋昌江. 基于双目视觉的三维物体表面测量系统设计与实现[D]. 哈尔滨:哈尔滨工业大学, 2012.
[16]Scharstein D, Szeliski R. High-accuracy stereo depth maps using structured light[A].Computer Vision and Pattern Recognition, 2003. Proceedings[C]. 2003 IEEE Computer Society Conference on. IEEE, 2003:I-195-I-202 vol.1.
[17]于晓洋, 单鹂娜, 曹沈楠,等. 结构光时间编码技术进展[J]. 哈尔滨理工大学学报, 2010, 15(1):98-102.
[18]宋昌江. 基于双目视觉的三维物体表面测量系统设计与实现[D]. 哈尔滨:哈尔滨工业大学, 2012.

