矩形钢套筒约束混凝土轴心受压应力应变关系
(1.重庆大学 a.山地城镇建设与新技术教育部重点实验室;b.土木工程学院,重庆 400045;2.后勤工程学院 军事土木工程系, 重庆 401311)




1 试验研究
1.1 试件设计


图1 设矩形钢套筒的剪力墙示意图Fig.1 Sketch of the shear wall with rectangle steel
为保证剪力墙水平分布筋能够伸入边缘构件进行锚固,钢套筒在靠近腹板一侧须采用缀板进行连接,设计了3个带缀板的钢套筒约束混凝土试件(A组)。考虑到带钢套筒型钢混凝土剪力墙在实际受力过程中,钢套筒内部靠缀板一侧的混凝土除了受到缀板的约束以外,还受到腹板区域混凝土的有效约束,其实际受力情况可能与全封闭的钢套筒约束混凝土试件更为接近,为此,又设计了3个全封闭的钢套筒约束混凝土试件(B组)。
图2给出了两组试件的示意图。所有试件内部混凝土横截面长240 mm,宽90 mm,钢板厚5 mm,缀板厚10 mm,钢板与钢板间、钢板与缀板间均采用焊接。所有试件套筒高h=400 mm,为保证钢套筒不直接承受轴向力,在试件的上下两端,混凝土凸出钢套筒10 mm,试件总高度为420 mm。

图2 试件示意图
试件中采用的钢板为Q235钢,根据《金属材料拉伸试验第1部分:室温试验方法》(GB/T 228.1—2010)[18]标准,制作了3个标准拉伸试样。拉伸试验在重庆大学材料学院建材试验室完成,根据3个试样的拉伸试验数据计算得到的钢材屈服强度和弹性模量的平均值见表1。混凝土设计强度为C40,浇筑试件时,预留了3个标准立方体试块,标准试块和试件在相同条件下养护20 d,在试验加载当天对标准试块进行强度测试。测试在重庆大学土木工程学院岩土试验室完成,取3个标准试块立方体抗压强度的平均值作为混凝土立方体强度fcu,结果见表1。

表1 材料参数表Table 1 Properties of materials
1.2 试验加载及测量内容
由于钢套筒在剪力墙中所处区域为墙体受压侧底部边框区域,其受力状态接近于单轴受压,因此,试验中所有试件均采用电液伺服压力试验机YAS-500轴向单调加载。试验采用力控制加载,当轴力小于500 kN时,每级增加100 kN;当轴力在500~800 kN时,每级增加50 kN;当轴力大于800 kN时,每级增加20 kN。试验在重庆大学结构实验室完成,试验装置如图3所示。
试验中,测量内容包括:试件的轴向力、轴向变形和钢套筒的应变。为测量试验过程中钢套筒的应变状态,在试件的长边和短边方向沿纵向均匀布置了应变片,应变片布置如图4所示。轴向力和轴向变形由试验机自动采集,钢套筒的应变通过DH3816静态应变采集仪进行采集并保存。

图3 加载装置Fig.3 Loading device

图4 应变片布置图Fig.4 Strain gages arrangement of
2 试验结果及分析
2.1 试验现象


图5 试件照片
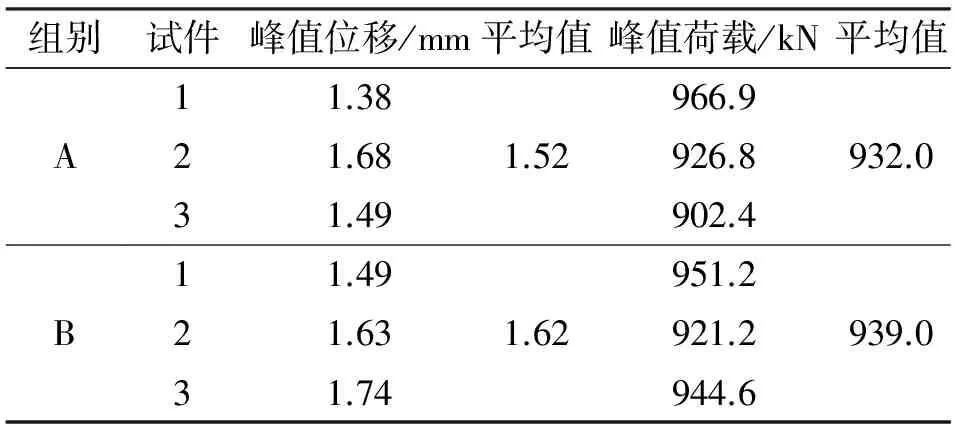
表2 试件峰值荷载和峰值位移Table 2 Peak load and peak displacement of specimens

图6 力位移曲线和应力应变曲线Fig.6 Force-displacement curves and stress-strain

2.3 应力分析
试验过程中,各试件钢套筒短边及长边各测点的对应方向应变测试结果均比较接近,将短边及长边应变结果取均值后,得到加载过程中各试件钢管应变与试件轴向荷载关系如图7所示,受拉为正,受压为负。

图7 钢管应变轴向荷载曲线Fig.7 Curves of the steel tube strain-axial


图8 试件钢管应力荷载曲线Fig.8 Curves of steel tube stress-load of specimens
(1)
(2)
从图7和图8可以看出:当轴向荷载达到峰值时,带缀板试件长边钢管横向应力为74.1 MPa,短边钢管横向应力为101.4 MPa;全封闭的钢管应力在各个方向上均比带缀板的偏大一点,其长边钢管横向应力为114.3 MPa,短边钢管横向应力为133.5 MPa。最大应力出现在全封闭试件短边,其横向拉应力为133.5 MPa,纵向压应力为48.4 MPa,折算应力为163 MPa。

3 核心区混凝土应力应变关系
3.1 基本方程
(3)
(4)
(5)
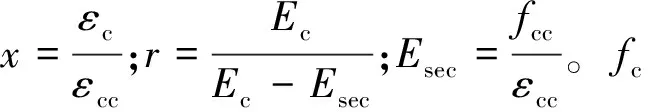
(6)
式中:fl为等效侧向约束力,指截面整体的等效侧向约束力;ke为与截面整体形状有关的有效约束系数。
3.2 有效约束系数
约束系数定义为[12]
(7)
式中:Ae为核心混凝土有效约束区面积;Ac为核心混凝土总面积。
参照文献[12],方形钢套筒约束构件的核心混凝土约束模型如图9(a)所示,图中阴影部分为约束区,假定核心混凝土距角部0.1倍总长范围内为有效约束区,而距边缘0.1~0.9倍总长范围内为非约束区,非约束区曲线为起始点处与边夹角为45°的抛物线。假定矩形钢套筒约束试件的核心混凝土的约束模型仍满足文献[12]的规定,可得矩形钢套筒约束构件有效约束区如图9(b)所示。

图9 约束模型示意图Fig.9 Diagram of confined
为验证上述关于矩形钢套筒有效约束区计算方法的合理性,采用大型通用有限元软件ABAQUS,建立三维实体模型进行分析。有限元模型中,混凝土材料采用塑性损伤模型,钢板采用经典弹塑性模型,混凝土单元为C3D8,钢套筒单元为S4,将核心区混凝土及钢套筒沿截面宽度方向划分为5个单元,沿截面长度方向划分为13个单元;沿柱高方向,将核心混凝土划分为21个单元,将钢套筒划分为20个单元。有限元模型中钢套筒与内部混凝土之间采用切向无摩擦、法向硬接触的接触属性,有限元模型图如图10所示。核心区混凝土底面建立轴向固定约束,顶面施加轴向压缩位移,模拟轴向加载下钢套筒对混凝土的约束情况。

图10 有限元模型
模拟结果表明,在轴压力作用下,矩形截面角部区域混凝土的约束效果最强,长边中点处约束最弱,钢套筒内部混凝土的约束情况如图11所示,与图9(b)所示约束模型基本一致,说明本文关于矩形钢套筒约束混凝土试件有效约束区的假设是合理的。
图11 矩形钢套筒约束混凝土有限元模拟示意图Fig.10 Finite element simulation diagram of the rectangular steel tube confined
根据图9(b)所示,经几何计算,核心混凝土有效约束区的面积为
Ae=L×D-0.213(L2+D2)
(8)
3.2 等效约束力

(9)
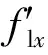
(10a)
(10b)
式中:t为钢管壁厚;σxhp和σyhp分别为峰值力时长边和短边钢管的横向应力。

图12 矩形钢管横向受力图Fig.12 Transverse force diagram of rectangular steel
式(10)中钢套筒的横向应力可以参考文献[12]中的公式计算。需要说明的是,文献[12]中的公式是针对方形钢管约束混凝土提出来的,其两个方向长度和厚度均相等,因此,在回归分析钢管应力与钢管宽厚比的时候,并没有区分长短边方向。矩形钢管与方形钢管有所不同,短边方向钢管中的力是因长边方向混凝土与钢管之间的相互作用而产生的(如图12所示),所以,计算短边方向钢管的横向应力时,应该采用长边方向的边长,计算长边方向的横向应力采用短边方向的边长。
σxhp= 0.1(D/t)0.5f215
(11a)
σyhp= 0.1(L/t)0.5f215
(11b)
式中:f215为Q235钢材的设计强度,f215=215 MPa。
4 方法的验证
将式(11)计算得到的矩形钢套筒约束混凝土试件的钢管横向应力与试验结果进行对比,如表3所示。结果表明,长边方向的理论计算值稍比试验值偏小,短边方向理论计算值稍比试验值偏大,但误差均在可接受范围之内,说明采用式(11)计算钢套筒横向应力是合理的。

表3 等效约束力Table 3 Equivalent confined force
2)根据式(7)~式(8),计算出有效约束系数ke;
3)根据式(6),计算出有效侧向约束力fl;



图13 计算的约束混凝土应力应变曲线与全封闭试件的试验曲线对比Fig.13 The contrast of computation stress-strain curve of confined concrete and test curve of totally enclosed
5 结论
根据试验结果和理论分析,可以得到以下结论:


参考文献:
[1] MANDER J B, PRIESTLEY M J N, PARK R. Observed stress-strain behavior of confined concrete [J]. Journal of Structural Engineering, 1987, 114(8):1827-1849.
[2] MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete [J]. Journal of Structural Engineering, 1988, 114(8):1804-1826.

SHI Q X, WANG N, TIAN Y, et al. Study on stress-strain relationship of high-strength concrete confined with high-strength stirrups under axial compression [J]. Journal of Building Structures, 2013,34(4):144-151.(in Chinese)
[4] SAATCIOGLU M, RAZVI S R. Strength and ductility of confined concrete [J]. Journal of Structural Engineering, 1992, 118(6):1590-1607.
[5] SRINIVASAN C N, SCHNEIDER S P. Axially loaded concrete-filled steel tubes [J]. Journal of Structural Engineering, 1999, 125(10):1202-1206.
[6] 蔡健,龙跃凌.带约束拉杆矩形钢管混凝土的本构关系[J].工程力学,2008,25(2):137-143.
CAI J , LONG Y L. Constitutive relationship of rectangular CFT columns with binding bars [J]. Engineering Mechanics,2008,25(2):137-143.(in Chinese)
[7] 郭小平.矩形钢管混凝土中核心混凝土的本构关系[J].湖南交通科技,2011, 37(2):74-79.
GUO X P. Constitutive relationship of concrete core confined by rectangular steel tube [J]. Hunan Communication Science and Technology, 2011, 37(2): 74-79. (in Chinese)
[8] FENG P, CHENG S, BAI Y. Mechanical behavior of concrete-filled square steel tube with FRP-confined concrete core subjected to axial compression [J]. Composite Structures, 2015, 123: 312-324.
[9] KATWAL U, TAO Z, HASSAN M K. Simplified numerical modelling of circular concrete-filled steel tubular stub columns [M]. Mechanics of Structures and Materials: Advancements and Challenges, CRC Press, 2016: 223-230.
[10] XIAO Y, TOMII M, SAKINO K. Experimental study on the design method to prevent the shear failure of reinforced concrete short circular columns by confining in steel tube [J]. Transactions of the Japan Concrete Institute, 1986, 8: 535-542.
[11] 张素梅,刘界鹏,马乐.圆钢管约束高强混凝土轴压短柱的试验研究与承载力分析[J].土木工程学报, 2007, 40(3): 24-31.
ZHANG S M LIU J P MA L XING T. Axial compression test and analysis of circular tube confined HSC stub columns [J]. China Civil Engineering Journal, 2007, 40(3): 24-31. (in Chinese)
[12] 周绪红,甘丹,刘界鹏,等.方钢管约束钢筋混凝土轴压短柱试验研究与分析[J].建筑结构学报, 2011, 32(2): 68-74
ZHOU X H, GAN D, LIU J P, et al. Experiment and analysis on square tubed reinforced concrete stub columns under axial compression [J]. Journal of Building Structures, 2011, 32(2): 68-74. (in Chinese)
[13] HANY N F, HANTOUCHE E G, HARAJLI M H. Axial stress-strain model of CFRP-confined concrete under monotonic and cyclic loading [J]. Journal of Composites for Construction, 2015, 19(6): 04015004.
[14] LU Y, LI N, LI S, et al. Behavior of steel fiber reinforced concrete-filled steel tube columns under axial compression [J]. Construction and Building Materials, 2015, 95: 74-85.
[15] SHIRMOHAMMADI F, ESMAEILY A, KIAEIPOUR Z. Stress-strain model for circular concrete columns confined by FRP and conventional lateral steel [J]. Engineering Structures, 2015, 84: 395-405.
[16] ZIAADINY H, ABBASNIA R. Unified cyclic stress-strain model for FRP-confined concrete circular, square and rectangular prisms [J]. Structural Concrete, 2016, 17(2): 220-234.
[17] AFIFI M Z, MOHAMED H M, BENMOKRANE B. Theoretical stress-strain model for circular concrete columns confined by GFRP spirals and hoops [J]. Engineering Structures, 2015, 102: 202-213.
[18] 中华人民共和国国家质量监督检验检疫总局.金属材料拉伸试验第1部分:室温试验方法:GB/T 228.1―2010 [S]. 北京:中国标准出版社,2010.
General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. Metallic materials-Tensile testing-Part 1: Method of test at room temperature: GB/T 228.1-2010 [S]. Beijing:Standards Press of China,2010. (in Chinese)

