含浅层强透水层堤基的上覆砂层管涌破坏试验研究
(1.重庆三峡学院 土木工程学院,重庆 404100;2.武汉大学 水利水电学院, 武汉430072;3.河海大学 环境学院,南京 210098)
管涌是指地基土体在渗流作用下,填充在土体骨架中的细颗粒被渗流水带走并形成集中渗流通道的地质现象。大量洪灾资料表明,在大堤洪灾中,管涌险情数量最多,分布范围广,且易诱发重大险情,甚至导致大堤溃口,是江河大堤在汛期危害最大的险情之一[1]。1998年,长江干流和洞庭湖区堤防分别出现险情698和626处,其中,管涌分别为366和343处,分别占52.44%、54.79%[2]。因此,研究堤基上覆土层管涌破坏的发生、发展及破坏机理,优化管涌的预防及治理措施具有重大意义。由于江河上的堤坝工程多坐落于双层堤基上,学者们意识到有必要针对双层堤基管涌破坏进行研究。通过有限元、离散元等数值模拟软件或砂槽模拟试验研究管涌破坏过程及机理,如罗玉龙等[3]、陈建生等[4]、李广信等[5]、梁越等[6]借助砂槽模拟试验分别观察了管涌的破坏过程,通过分析试验中的参量研究管涌的破坏机理。胡亚元等[7]、陈生水等[8]、周晓杰等[9]、周健等[10]、刘昌军等[11]分别采用Galerkin、FEG、PFC3D、GWSS等数值模拟软件建立双层堤(坝)基管涌动态破坏过程,得出管涌破坏与堤身长度、各层堤基的厚度、堤坝两侧水头差的关系。此外,美国[12]、日本[13]、德国[14]、荷兰[15]等国学者也针对双层堤基的管涌机理进行试验研究,并取得部分成果。但上述学者们主要研究对象为单、双和多层堤基,目前针对局部区域存在埋藏较浅的强透水层的堤基管涌破坏过程及机理的研究还较少见。经大量调查资料显示,堤基中局部区域含有浅层强透水层的情况亦较为普遍,如长江中下游堤防[5]、珠江的北江大堤[16]、江西省九江市城防堤、湖南省安造垸堤防、湖北省孟溪垸堤防、湖北省簰洲湾堤防[17]、湖北洪山武金堤和安徽鲁港大堤[18],亟待深入研究。
以局部存在浅层强透水层的砂土堤基为研究对象,借助室内砂槽模型试验,观察堤基管涌破坏的过程,并通过筛分试验和静力触探试验探讨研究管涌破坏的机理,从而提出防治方案及治理措施。
1 材料与方法
1.1 材料特性
室内管涌试验共计3种材料:砂卵砾石、砂土、聚乙烯透明塑料纸,其中砂卵砾石和砂土构成局部区域含有浅层强透水层的堤基结构,垂直防渗体和堤身采用聚乙烯透明塑料纸代替。土体均取自长江堤防重庆万州段左岸,经室内筛分试验,作砂卵砾石和砂土的颗粒级配曲线,如图1所示。
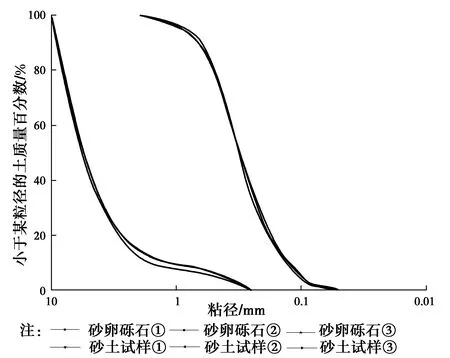
图1 砂卵砾石和砂土的颗粒级配曲线Fig.1 The grading curve of sand and cobble and
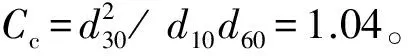
通过烘干法测得土体的含水率、干密度,将土样的基本物理性质指标列入表1。

表1 试验用土的基本物理性质指标Table 1 Basic physical property indexes of soil used in test
由表1可知,砂土和砂卵砾石的渗透系数分别为5.07×10-5m·s-1、5.18×10-3m·s-1,砂卵砾石的渗透系数为砂土的102.17倍,砂土为相对弱透水层,砂卵砾石为相对强透水层(下文简称强透水层)。
1.2 试验方法
1.2.1 试验装置 试验装置用于模拟局部含有浅层强透水层的堤基渗流过程,观察管涌破坏过程和研究该特定堤基的管涌破坏机理。砂槽模型试验布置如图2所示。

图2 砂槽模型试验布置图Fig.2 Arrangement plan of sandbox model
由图2可得,试验装置由砂槽、测压板、高位水塔组成。砂槽由透明的有机玻璃板和角钢构成,试验砂槽呈“鞋形”,左端为水箱,高于右端。砂槽为长100 cm,宽30 cm,左端高90 cm,右端高50 cm,将砂槽底部高程记为±0 cm。砂土和砂卵砾石分层填筑,构成含有局部浅层强透水层的地基,砂卵砾石厚度为15 cm,砂卵砾石底部高程为5 cm,距离砂槽右壁25 cm。砂卵砾石上覆砂土层厚度为8~20 cm。聚乙烯透明塑料纸深入堤基中,底端高程为20 cm,顶端与水箱侧壁相连接。
高位水塔蓄水量为0.85 m3,借助进水管向左端水箱引水,模拟河堤靠近河道一侧的河流水位。水箱的侧壁上设置了水位调节管,高程为40 cm。砂槽右端设置有排水管,高程为40 cm,为避免在排水过程中将表层细砂带走,排水管用纱布包裹。砂槽中布置22个多孔进水型铝管测压计,并与测压管相连接,得出各监测点的孔隙水压力值[10]。测压监测点的编号分别为A1-A4、B1-B4、C1-C4、 D1-D4、E2-E3、 F1-F4。
水箱水位h分别为42~60 cm,每隔2 cm设置一水头,共计10个。试验主要观察含有局部浅层强透水层堤基的管涌破坏过程,研究堤基管涌破坏机理,不考虑堤身的渗流,堤身用聚乙烯透明塑料纸和有机玻璃板代替。水位调节管和进水管共同调控水箱的水位。测压管中滴入红色试剂,便于精确读数。
1.2.2 试验步骤
1)布置垂直防渗体。采用透明胶水将聚乙烯透明塑料纸两侧固定在水箱侧壁,并用透明胶带加固,防止接缝处渗漏。
2)堤基填筑及多孔铝管测压计的安装。堤基填筑通过干密度、土料含水率控制,按照图2(a)所示进行分层压实;填筑过程中,在22个测压监测点安装多孔进水型铝管测压计。
3)蓄水及测压管排气。打开进水阀,开始蓄水,将水箱调控至预设水位。读数前应将测压管(透明橡胶管、硬塑料管)中的气泡排净,精确读数。
4)读数。通过烧杯量测排水管的流量(即渗流量)。为减小孔隙水压力读数误差,进行多次读数,求取均值。同理,读取3次测压监测点的水头,求取平均值。
5)观察渗透管涌破坏过程。观察上覆砂层渗透破坏的发生及发展,借助高清照相机拍摄强透水层上覆砂土在各水头下的渗流情况。
6)试验对比分析。取A点区域的砂土进行静力触探试验和颗粒筛分试验,测出锥头阻力和各粒径砂土所占的百分比。
7)多次测量点A的高程,求取平均值。
8)改变水箱水位h,重复步骤1)~7)。
2 理论计算及试验结果
2.1 理论计算
采用Koenders模型为理论基础,基于工程实际和物理模型,发展了Sellmeijer的模型,推导得出临界水力梯度公式见式(1)。
(1)
(2)
式中:Hcrit为临界水头;L为渗流长度;γp为土粒重度;γw为水的重度;θ为休止角;d为土颗粒平均粒径;k为渗透系数;η为阻力系数。
将式(2)带入式(1)可得
(3)
试验中,L取75 cm,γp取28.7 kN/m3,γw取9.8 kN/m3,θ取35°,d取0.42 mm,k取5.07×10-5m·s-1,将参数带入式(3),计算得到砂土的临界水力梯度ic=0.152。
2.2 试验结果
试验中采用逐级升高水箱水位的方式来驱动渗流及渗透破坏的发生过程,从42 cm一直增大至60 cm,观察渗流现象。当在该级水头下渗流稳定后,再抬高至下一级水头进行试验,每次抬升2 cm。根据渗流量和各测压管读数是否发生变化,判定堤基渗流是否达到稳定状态。当各级水头达到稳定状态下,记录各级水位值、测压管读数和堤基渗流量,将结果列入表2。J为平均渗透比降J=h/L,式中L为最短渗径,即为管涌口到进水面的最短距离,试验中L取75 cm。

表2 渗流量Q及渗透坡降JTable 2 Seepage discharge and seepage gradient
3 试验现象分析
借助高清照相机对管涌发生前、管涌发展过程进行拍照,利用图像观察细砂颗粒在砂土颗粒间的移动现象,各水位下拍摄得到的典型图像如图3所示。

图3 表层砂土管涌图Fig.3 The piping graph of medium sand on surface
由图3可得,砂土层渗流过程可以分为几个阶段:
1)稳定渗流阶段(42 cm≤h<48 cm),如图3(a)所示。在该阶段A点的渗透坡降从0.034逐渐升高至0.133,小于砂土的临界水力梯度ic=0.152。渗流初期砂土表层有浑水冒出,在砂土颗粒骨架间有气泡在移动,一些细小的粉土颗粒随着渗流水移出土体骨架颗粒,15 min后渗水逐渐清澈。将水箱水位升高至48 cm时,A处砂土骨架颗粒间有细小砂粒开始出现轻微的翻滚,但由于渗透坡降较小,细颗粒并未随渗流水流走。
2)细颗粒流失阶段(48 cm≤h<52 cm),如图3(b)所示。A点的渗透坡降由0.166升高至0.199,JA大于临界水力梯度ic=0.152,砂层发生管涌破坏,管涌范围相对较小,靠近强透水层的砂土中的细颗粒在渗透力的作用下翻滚“沸腾”,细颗粒随渗水从管涌口逐渐流失。从图3不难看出,靠近砂卵砾石表层的砂土仅剩下粗颗粒,能清晰的反映出砂土层的骨架颗粒。
3)较细颗粒流失阶段(52 cm≤h<58 cm),如图3(c)所示。A点的渗透坡降在上一阶段的基础上进一步增大至0.289,从图中清晰可见,管涌通道呈“V”型,较细颗粒随着渗水进一步流失,砂土骨架颗粒与砂卵砾石层联通成一优先渗流通道。
4)管涌破坏扩大阶段(58 cm≤h≤60 cm),如图3(d)所示。渗透坡降升高到0.331,为临界水力梯度的2.18倍。对比图3(c)和图3(d)可得,在该水利梯度下管涌破坏范围进一步扩大,管涌破坏仍呈现“V”型。
4 堤基渗流场与颗粒级配分析
4.1 堤基渗流场分析
通过烧杯量测排水管的流量,即得到堤基渗流量,作渗流量随水箱水位的变化曲线如图4所示。

图4 堤基渗流量随水箱水位的变化曲线Fig.4 The change curve of seepage discharge of dike foundation under different water block
当处于稳定渗流阶段(H-I)时,渗流量很小,流速缓慢,随上游水头的上升呈线性增长,经拟合Q随h变化的函数表达式为:Q=0.267h-10.65,可见在稳定渗流阶段其渗透系数未发生改变。随着水箱水位进一步升高,砂土层发生管涌破坏,渗流进入细颗粒流失阶段(I-J),渗流量突然增大,偏离H-I阶段的线性函数,砂土的渗透系数明显增大。
最后进入较细颗粒流失阶段(J-K)和砂层管涌破坏扩大阶段(K-L)。在后3个阶段中,渗透系数相比稳定渗流阶段都有较为明显的增大趋势,Q随h变化的函数表达式分别为:Q=0.505h-22.034、Q=0.65h-29.6、Q=0.75h-35.4。
根据测压管水头(多次读数求取平均值)计算得出图2(a)中点A的渗透坡降JA,作渗透坡降JA随水箱水位h的变化曲线如图5所示。
由图5可得,渗透坡降JA随水箱水位h的变化规律同图4一致,同样分为渗流稳定阶段、细颗粒流失阶段、较细颗粒流失阶段、砂层管涌扩大阶段,各阶段近似呈线性变化,其表达式分别为:JA=0.016h-0.624、JA=0.03h-1.3、JA=0.038 6h-1.738、JA=0.055h-2.685;每一阶段的变化规律在此不再赘述。

图5 渗透坡降随水箱水位的变化曲线Fig.5 The change curve of seepage gradient of dike foundation under different water block
4.2 管涌处砂土颗粒级配分析
第3节已经针对试验过程的现象进行了详细描述,4.1小节中针对渗流量Q和砂土表层A点处的渗透坡降JA进行分析,分析得到在渗流稳定阶段未发生渗透破坏,随着水箱水位的升高,表层砂土逐渐发生管涌破坏。由此可知,渗透系数的增大导致渗流量增加,砂土骨架颗粒间的间隙决定了渗透系数的大小。在不同水箱水头下,取A点附近区域的砂土层进行筛分试验,将结果列入表3。

表3 砂土各粒径所占百分比Table 3 The percentage of particle size sand
基于表3中各粒径砂土所占百分比,作 A点处砂土在试验前后的颗粒级配曲线,如图6所示。

图6 试验前后砂土的颗粒级配曲线Fig.6 The grading curve of sand before and after the
结合表3和图6可得,当堤基处于稳定渗流阶段(42 cm≤h<48 cm)时,0.034≤J<0.128,J 当堤基处于细颗粒流失阶段(48 cm≤h<52 cm)时,0.128≤J<0.247,超过允许值,在该阶段随着水箱水位的升高,逐渐发生管涌破坏,由表2和图6可得0.05 同理,当堤基处于较细颗粒流失阶段(52 cm≤h<58 cm),0.247≤J<0.476,对比曲线2和曲线3可得,0.075 锥头阻力在静力触探试验中扮演重要角色,通过锥头阻力能获得岩土体力学参数,能表征土体的级配状况。采用静力触探试验获取试验前后砂土层的锥头阻力值,作砂土层锥头阻力随深度的变化如图7所示。 图7 管涌前后砂土的锥头阻力Fig.7 Cone resistance of sand before and after 砂土属粗颗粒土,没有内聚力,其抗剪强度的大小主要取决于内摩擦角,锥头阻力的表达式为 qc=σv0Nq (4) 式中:σvo为土层上覆压力,kPa,和土层的深度有关;σvo=γh;Nq为对砂土的无量纲锥头阻力系数。 由图7可得,各阶段下砂层的锥头阻力都随着贯入深度的增加而增大,同式(4)的规律相符。对比各阶段的锥头阻力的变化规律可得,随着管涌破坏的发展,砂土骨架颗粒间的细颗粒逐渐流失,锥头阻力逐渐变小。由此可见,由于管涌破坏,砂土层中的细颗粒被带走,土体颗粒间的相互作用力发生改变,锥头阻力下降。 随着水箱水位的升高,A点区域砂土的渗透坡降随之增大,砂土层逐渐发生管涌破坏,改变砂土骨架颗粒的应力状态,A点高程逐渐减小,作点A的高程随水箱水位的变化曲线,如图8所示。 图8 点A的高程随水箱水位的变化曲线Fig. 8 The change curve of elevation of point A under different water block 由图8可得,在各阶段A点高程随水箱水位变化的规律一致,都是随着水箱水位的升高而降低,总沉降为8.67 cm。但也存在不同,其沉降速度存在明显的区别,1~4阶段的沉降量分别为:1.97、1.82、3.53、1.35 cm,分别占总沉降的22.72%、20.99%、40.72%、15.57%。由此可见,管涌出口处砂层的主要沉降发生在较细颗粒流失阶段。 1)局部浅层强透水层易形成优先渗流通道,其上覆较薄砂土层易被“击穿”,即发生管涌破坏。管涌破坏分为稳定渗流阶段、细颗粒流失阶段、较细颗粒流失阶段、管涌破坏扩大阶段;其中,稳定渗流阶段无砂颗粒流失,后3个阶段分别流失0.05 2)随着管涌破坏的发展,砂土中的细颗粒流失,砂土渗透系数上升,渗流量和渗透坡降快速增大,且在各阶段近似呈线性变化;锥头阻力逐渐变小,砂土层发生沉降,且最大沉降发生在较细颗粒流失阶段。 堤基中若存在强透水层时,应给予足够的重视,采取增大防渗墙深度截断强透水层或设置反虑等措施,防止发生管涌破坏。 参考文献: [1] 张刚. 管涌现象细观机理的模型试验与颗粒流数值模拟研究[D]. 上海:同济大学, 2007. ZHANG G. Research on meso-scale mechanism of piping failure by means of model test and PFC numerical simulation [D]. Shanghai:Tongji University, 2007. (in Chinese) [2] 王霜, 陈建生, 黄德文, 等. 土层结构对管涌发展影响的试验研究[J]. 岩土工程学报, 2013, 35(12): 2334-2341. WANG S, CHEN J S, HUANG D W, et al. Experimental study on piping development considering effect of foundation structure[J]. Chinese Journal of Geotechical Engineering, 2013, 35(12): 2334-2341. (in Chinese) [3] 罗玉龙, 吴强, 詹美礼, 等. 渗流-侵蚀-应力耦合管涌试验装置的研制及初步应用[J]. 岩石力学与工程学报, 2013, 32(10): 2108-2114. LUO Y L, WU Q, ZHAN M L, et al. Development of seepage-erosion-stress coupling piping test appartus and its parimary application[J]. Chinese Journal of Rock, Mechanics and Engineering, 2013, 32(10): 2108-2114. (in Chinese) [4] 陈建生, 何文政, 王霜, 等. 双层堤基管涌破坏过程中上覆层渗透破坏发生发展的试验与分析[J]. 岩土工程学报, 2013, 35(10): 1777-1783. CHEN J S, HE W Z, WANG S, et al. Laboratory tests on development of seepage failure of overlying layer during piping of two-stratum dike foundation [J]. Chinese Journal of Geotechical Engineering, 2013, 35(10): 1777-1783. (in Chinese) [5] 李广信, 周晓杰. 堤基管涌发生发展过程的试验模拟[J]. 水利水电科技进展, 2005, 25(6): 21-24. LI G X, ZHOU X X. Laboratory simulation on generation and evolution of piping in embankment foundation [J]. Advances in Science and Technology of Water Resources, 2005, 25(6): 21-24. (in Chinese) [6] 梁越, 陈亮, 陈建生. 考虑流固耦合作用的管涌发展数学模型研究[J]. 岩土工程学报,2011,33(8):1265-1270. LIANG Y, CHEN L, CHEN J S. Mathematical model for piping development considering fluid-solid interaction [J]. Chinese Journal of Geotechical Engineering, 2011, 33(8):1265-1270. (in Chinese) [7] 胡亚元, 马攀. 三相耦合渗流侵蚀管涌机制研究及有限元模拟[J]. 岩土力学, 2013, 34(4): 913-921. HU Y Y, MA P. Mechanism study and finite element simulation of three-phase coupling seepage erosion piping [J]. Rock and Soil Mechanics, 2013, 34(4): 913-921. (in Chinese) [8] 陈生水, 钟启明, 任强. 土石坝管涌破坏溃口发展数值模型研究[J]. 岩土工程学报,2009,31(5):653-657. CHEN S S, ZHONG Q M, REN Q. Numerical study on break development due to piping failure for earth-rock dams[J]. Chinese Journal of Geotechical Engineering, 2009, 31(5): 653-657. (in Chinese) [9] 周晓杰, 介玉新, 李广信. 基于渗流和管流耦合的管涌数值模拟[J]. 岩土力学,2009,30(10):3154-3158. ZHOU X J, JIE Y X, LI G X. Numerical simulation of piping based on coupling seepage and pipe flow[J]. Rock and Soil Mechanics, 2009, 30(10): 3154-3158. (in Chinese) [10] 周健, 周凯敏, 姚志雄, 等. 砂土管涌-滤层防治的离散元数值模拟[J]. 水利学报, 2010, 41(1): 17-24. ZHOU J, ZHOU K M, YAO Z X, et al. Numerical simulation of piping-filter prevention in sandy soil by discrete element method[J]. Journal of Hydraulic Engineering, 2010, 41(1): 17-24. (in Chinese) [11] 刘昌军, 丁留谦, 孙东亚, 等. 双层堤基管涌模型试验尺寸效应的数值模拟[J]. 岩石力学与工程学报, 2012, 31(Sup1): 3110-3116. LIU C J, DING L Q, SUN D Y, et al. Numerical simulation of size effect in piping erosion model test for double-startum dike foundations[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(Sup1): 3110-3116. (in Chinese) [12] SCHMERTMANN J H. No-filter factor of safety against piping through sands[J]. Geotechnical Special Publication,2000,111:65-132. [13] KOHNO I, NISHIGAKI M, TAKESHITAY. Levee failure caused by seepage and preventive[J]. Natural Disaster Science, 1987, 9(2): 55-76. [14] MULLER-KIRCHENBAUER H, RANKL M, SCHLOTZER C. Mechanism for regressive erosion beneath dams and barrages [C]// Proceefings of the 1st International Conference on Filters in Geotechnical and Hydraulic Engineering. Balkema, Rotterdam, Netherlands:[s.n.], 1993: 369-376. [15] DE WIT J M, SELLMEIJER J B, PENNING A.Laboratory testing on piping[C]// Proceedings of the 10th International Conference on Soil Mechanics and Foundation Engineering. Stockholm, Sweden:[s.n.], 1981: 517-521. [16] 刘杰, 谢定松, 崔亦昊. 江河大堤双层地基渗透破坏机理模型试验研究[J]. 水利学报, 2008, 39(11): 1211-1220. LIU J, XIE D S, CUI Y H.Failure mechanism of seepage in levees with double-layer foundation[J]. Journal of Hydraulic Engineering, 2008, 39(11): 1211-1220. (in Chinese) [17] 姚秋玲, 丁留谦, 孙东亚, 等. 单层和双层堤基管涌砂槽模型试验研究[J]. 水利水电技术, 2007, 38(2): 13-18. YAO Q L, DING L Q, SUN D Y, et al. Experinental studies on piping in single and two-stratum dike foundations [J]. Water Resources and Hydropower Engineering, 2007, 38(2): 13-18. (in Chinese) [18] 陈祖煜. 对长江干堤加固工程中一些问题的思考[J]. 水利水电科技进展, 2003, 23(4): 4-7. CHEN Z Y. Reflection on some problems in Yangtze River embankment reinforcement project [J]. Advances in Science and Technology of Water Resources, 2003, 23(4): 4-7. (in Chinese)5 堤基应力场分析
5.1 锥头阻力分析

5.2 管涌处砂土沉降分析
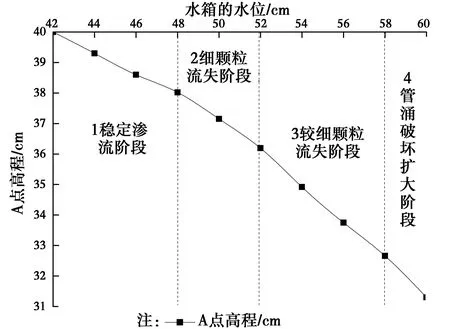
6 结论与建议

