考虑波纹板承载的导管架平台生活楼结构设计

朱本瑞，韩文秀，孙振平，李润野，黄锡玲，杨树耕

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 中海石油(中国)有限公司上海分公司，上海 200335)

生活楼作为海洋平台的重要组成部分，其作用是为平台工作人员提供生活、工作及休闲娱乐的场所[1].生活楼结构主要分为 3种类型：复合墙型、板架型、桁架型[2].复合墙型生活楼重量最轻，但其内部填充材料强度较弱，不适于恶劣的海上环境.板架型生活楼多用于自升式及半潜式等移动式平台，而桁架型是目前导管架平台生活楼最常见的形式，其主体结构一般采用高腹板 H型钢，立柱采用圆管或 H型钢，外壁采用斜撑及波纹板的组合形式[3].近期多个大型导管架平台设计表明，这种结构不仅用钢量大，造成成本增加，而且斜撑的布置会极大程度地限制生活楼外壁的开窗位置，影响上部人员的工作环境和舒适性[4].

王胜等[1]提出将移动式平台采用的板架型生活楼结构用于导管架平台，设计了板架式生活楼的底层强力板架，实现生活楼板架结构与平台上部组块的有效连接.宋杰等[5]针对控制海上生活楼结构重量的问题，对生活楼外壁材料进行改良，在满足规范要求的前提下合理降低生活楼重量.上述工作虽然可能在一定程度上降低生活楼结构的重量，但并未考虑波纹板承载，因此，减重效果有限.

波纹板是一种经冷加工成型的压型板，其沿波纹和垂直于波纹方向的力学性质具有明显差异，是一种各向异性板[6]，相对于普通平板具有良好的力学特性.郭彦林等[7]研究了波纹腹板在纯压和纯弯作用下的力学特性，证实了其具有良好的抗面外弯曲能力；对于波纹钢板墙，近年来国内外学者通过实验验证了其具有较大的抗弯刚度和抗压刚度，屈曲性能较优[8-9]；Farzampour等[10]研究表明，波纹钢板剪力墙具有较高的抗塑性变形能力；陶旭[11]基于ANSYS从板格层面验证了导管架平台生活楼常用波纹板具有类似的力学性能；在此基础之上，李润野[12]采用 ANSYS建立导管架平台整体生活楼结构，对比分析了不同生活楼模型在自重、地震加速度等垂向载荷以及侧向风载荷作用下的生活楼变形和应力；考虑波纹板非线性效应，国内外学者就波纹板的极限承载能力进行进一步的实验和数值分析，对波纹板极限承载能力的分析方法给出一定指导意义[13-14].

本文基于前人对波纹板力学性质的研究，首次提出取消生活楼斜撑、充分利用波纹板对结构提供有效支撑的设计方案.以导管架平台 120人生活楼为例，采用SACS建立该生活楼的三维有限元模型，通过计算，对比波纹板和斜撑对生活楼刚度和强度的贡献，证实了生活楼取消斜撑结构设计方案的可行性和合理性，研究成果为生活楼结构设计和重量优化提供了可行的方案和技术支持.

1 基于SACS的波纹板模拟

SACS软件在加强筋选项卡中提供了波纹板的功能，在 Precede操作页面中定义波纹板的各参数如图1所示，其中：A表示波纹板高度；B表示波纹板宽度；C表示波纹板跨距；D表示波纹板厚度.

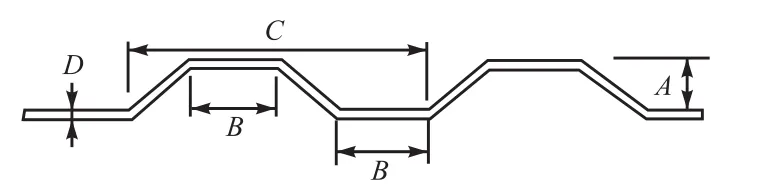
图1 波纹板各参数Fig.1 Parameters of corrugated panel

利用上述功能，在 SACS中定义波纹板各尺寸，建立导管架平台生活楼局部框架波纹板模型，其长为5.76,m，高为3.5,m.为对比不同网格划分密度对波纹板计算结果的影响，建立4种不同网格密度的框架波纹板模型，如图2所示.其中模型a不对波纹板进行划分；模型b水平方向将波纹板划分为4段，竖直方向划分为 2段，波纹板网格尺度为 1.44,m×1.75,m；模型c水平方向将波纹板划分为9段，竖直方向划分为 5段，网格尺度约为 0.64,m×0.70,m，水平方向近似等于波纹板一个波形的长度；模型 d网格最为精确，水平方向将波纹板划分为 55段，竖直方向划分为35段，网格尺度约为0.10,m×0.10,m.

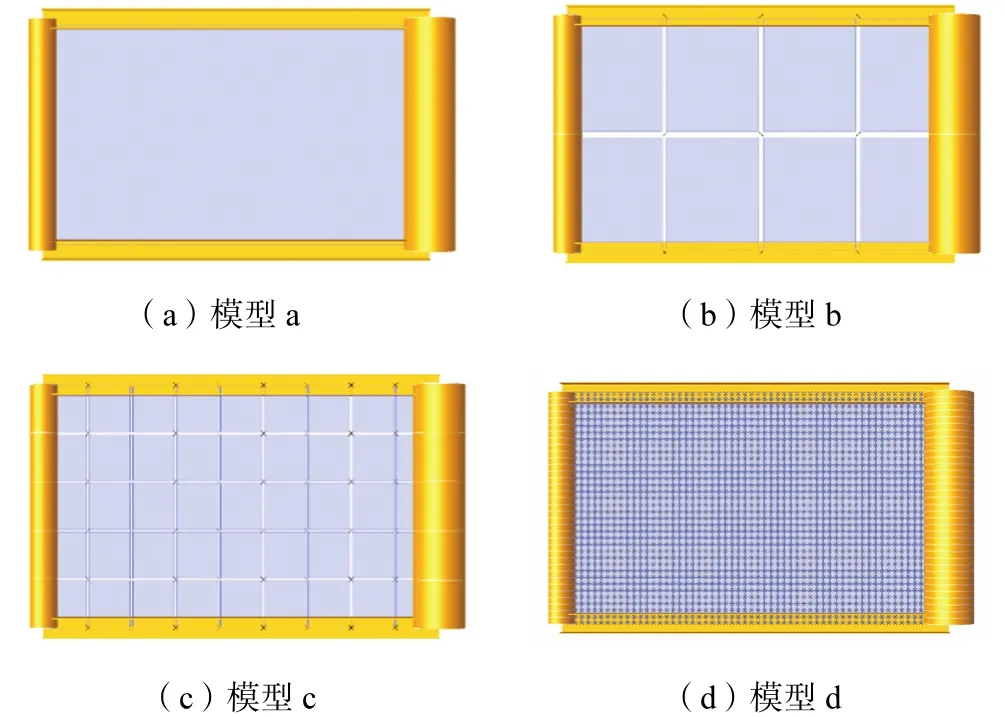
图2 不同网格划分密度的框架波纹板模型Fig.2 Models of corrugated frame panel with different mesh sizes

在SACS中定义2种工况，其中工况1为沿波纹的均布加载，工况 2为沿波纹的三角形载荷，2种工况的总载荷均为48,kN.分别提取4种模型在2种工况下的最大等效应力和最大位移，并以模型d的计算结果为基准，分别计算4种模型在2种工况下的最大等效应力差值和最大位移差值，结果如表1所示.

由表1的计算结果可知，模型a和模型b的波纹板网格划分较稀疏，便于建模，但计算结果误差较大.模型 d为基准模型，其网格密度最精确，但建模工作量较大.模型c计算得到的等效应力和位移与基准模型最接近，即采用模型c的网格尺寸已具有足够的精度且可在一定程度上提高建模效率.综合考虑工程建模的可操作性与计算效率精度，推荐采用模型c，即采用近似一个波纹长度的正方形网格尺寸对波 纹板进行模拟.

表1 不同网格SACS模型的结果对比Tab.1 Comparison results for SACS models with different mesh sizes

2 生活楼结构整体有限元模型

某导管架平台生活楼层高 3.5,m，共计 5层，带有直升机飞机甲板，其主尺度参数为：L=31,m，B=11.5,m，H=17.5,m.生活楼结构由主梁、立柱、垂向撑杆、斜撑和甲板板组成，生活楼四周外壁及内部各房间隔板为波纹板结构，其中靠近平台主体结构一侧的外壁为防爆波纹板，其余为普通波纹板.生活楼俯视示意图及有限元模型如图3所示.

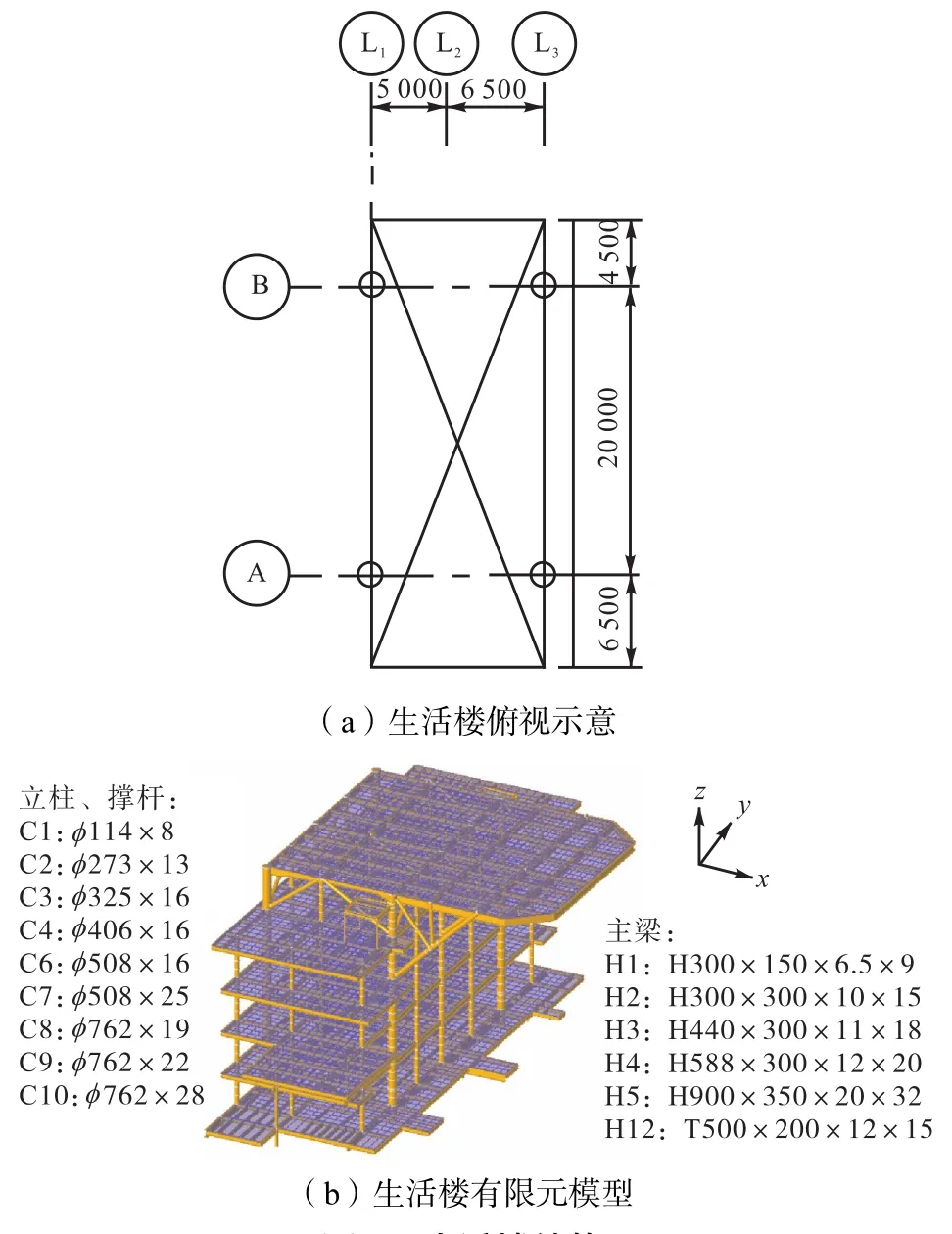
图3 生活楼结构Fig.3 Structure of living quarter

为论证本文提出的生活楼取消斜撑的新型结构设计方案，建立该生活楼的 3种有限元模型：模型 1为框架波纹板模型，该模型采用上述推荐波纹板网格划分尺寸建立了波纹板围壁，未建立垂向斜撑.模型2为框架斜撑模型，该模型建立了垂向斜撑，未建立波纹板围壁，是目前导管架平台生活楼结构常用分析方法.模型 3为框架无斜撑模型，是一个虚拟模型，作为对照，该模型的垂向斜撑和波纹板围壁均未建立.以生活楼L1排为例，3种结构有限元模型局部示意如图4所示.

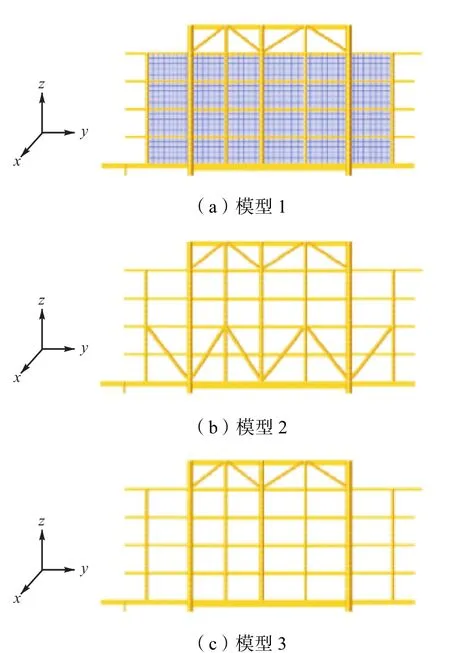
图4 生活楼L1有限元模型Fig.4 Finite element model of living quarter at L1

3 计算结果及波纹板斜撑的影响分析

根据文献[15]，对 3种生活楼模型进行在位工况下的对比分析，结构载荷包括自重、活载荷、设备载荷、风载荷和直升机载荷，其中直升机重量为 10.8,t，其降落载荷根据《DNV Rules for Classification of Ships：Part 6》[16]进行确定.考虑最不利组合工况及相应的组合系数，共计得到 88种载荷组合工况.提取 3种模型在各组合工况下的最大变形并对 3种模型各类杆件和模型1的波纹板进行强度分析.

为定量从结构刚度和结构强度 2个方面对波纹板和斜撑对生活楼框架结构的影响进行综合对比分析，本文提出刚度增强系数η和强度增强系数ε,这 2个指标，计算公式分别为

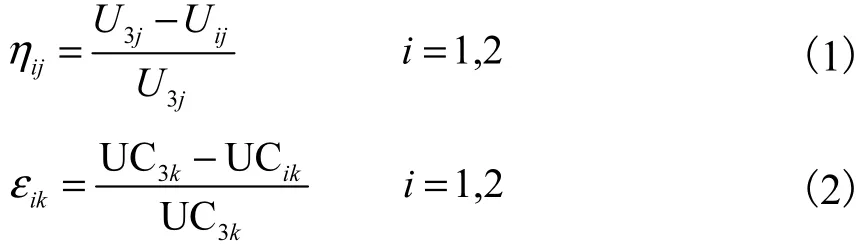
式中：ηij表示模型 i的第 j个工况下的刚度增强系数；U3,j表示模型3的第j各工况下节点最大变形值；Uij表示模型 i的同种工况下节点最大变形值；εik表示模型i的第k种构件的强度增强系数；UC3k为模型3第k种构件最大强度UC值；UCik为模型i的同种构件最大强度 UC值.ηij值和 εik值能够直观地描述波纹板或斜撑对生活楼框架结构的刚度和强度的贡献度，其数值在 0～1之间，越接近于 1说明其贡献度越大，反之则越小.

3.1 结构变形及刚度增强系数

提取各组合工况下3种模型的最大变形值，如图5所示.

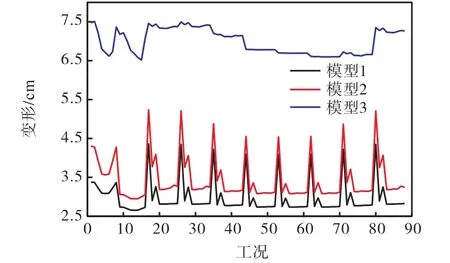
图5 生活楼最大变形值Fig.5 Maximum deformation of living quarter

由图5可知，模型1和模型2变形随工况变化规律基本相同，而参照模型 3仅为刚度较弱的框架结构，且不同方向其结构的刚度差异并不明显，因此变化规律有所差别.对比三者最大变形数值可知，模型3的变形值明显较大，最大值为7.51,cm，而模型1和模型 2变形值较小，最大值分别为 4.36,cm和5.24,cm，其均值约为模型3的1/3，显然，这是波纹板与斜撑结构能够提供良好的刚度造成的，相比较而言，模型 1的变形最小，说明波纹板较斜撑具有更好的刚度.

进一步计算各组合工况下模型 1和模型 2的刚度增强系数，结果如图6所示.

图6 刚度增强系数Fig.6 Stiffness enhancement coefficient

由图6可知，模型1和模型2的刚度增强系数平均值在0.5左右，且模型1的刚度增强系数在各工况下均大于模型2的刚度增强函数，说明生活楼取消斜撑模型具有更高的刚度.分析图6中模型1和模型2的刚度增强系数随工况的变化规律可知，两模型最小刚度增强系数均出现在工况 17、26、35、44、53、62、71和工况 80，一方面，这些工况均为操作工况，直升机载荷位于直升机甲板悬伸处最外边缘，此时直升机载荷远离生活楼重心，增加了生活楼结构所受弯矩，使其处于较危险的状态；另一方面，在这些工况下两模型的刚度增强系数差值较其他工况更大，说明生活楼在较危险工况下，波纹板在刚度上的优势更明显.

3.2 结构强度及强度增强系数

同理，对 3种模型杆件强度 UC值进行校核，提取生活楼在位工况下所有杆件的最大UC值，如表2所示.

表2 杆件最大UC值Tab.2 Maximum UC of members

由表 2可知，模型 1所有杆件强度 UC均小于1，在整个结构的15类构件中，仅对于C8和H4这2类构件强度 UC值相对模型 2有所增加，而剩余的13类构件强度UC均小于模型2，说明生活楼取消斜撑后不仅能够满足强度设计要求，且能够一定程度上改善传统生活楼结构的承载状态.由模型 3的结果可知，其结构已有多数构件强度UC值大于1.0，显然不满足规范的设计要求，这也从反面证实了波纹板在结构强度贡献上能够发挥非常有效的作用.

由式(2)计算所有杆件的强度增强系数，结果如图7所示.

由图7可知，波纹板和垂向斜撑对生活楼各构件均有强度贡献，强度增强系数平均在 0.5左右.总体而言，波纹板的强度贡献相对于斜撑的强度贡献更大，尤其是对于次要构件 C4、C9和 H1，其强度增强系数与斜撑的强度增强系数差值大于0.25，这说明波纹板对结构次要构件的强度贡献更加明显；而构件C8和 H4，波纹板的强度增强系数有所降低，为分析并说明其中原因，提取最危险工况下模型1和模型2所有杆件的应力分布，如图8所示.

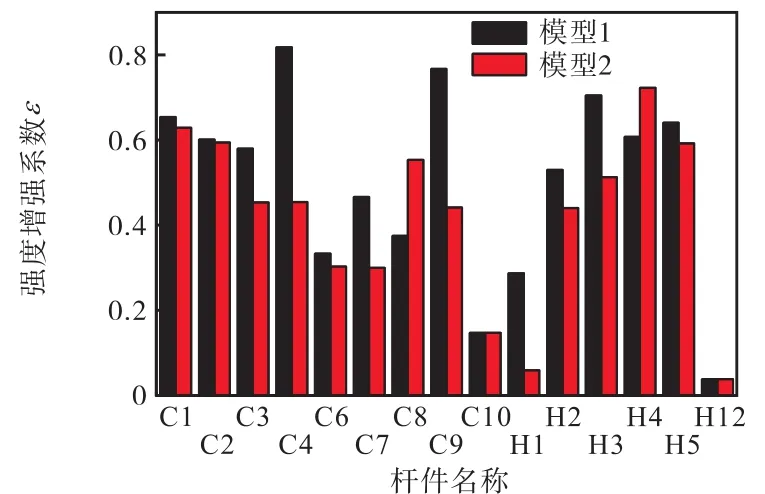
图7 强度增强系数Fig.7 Strength enhancement coefficient

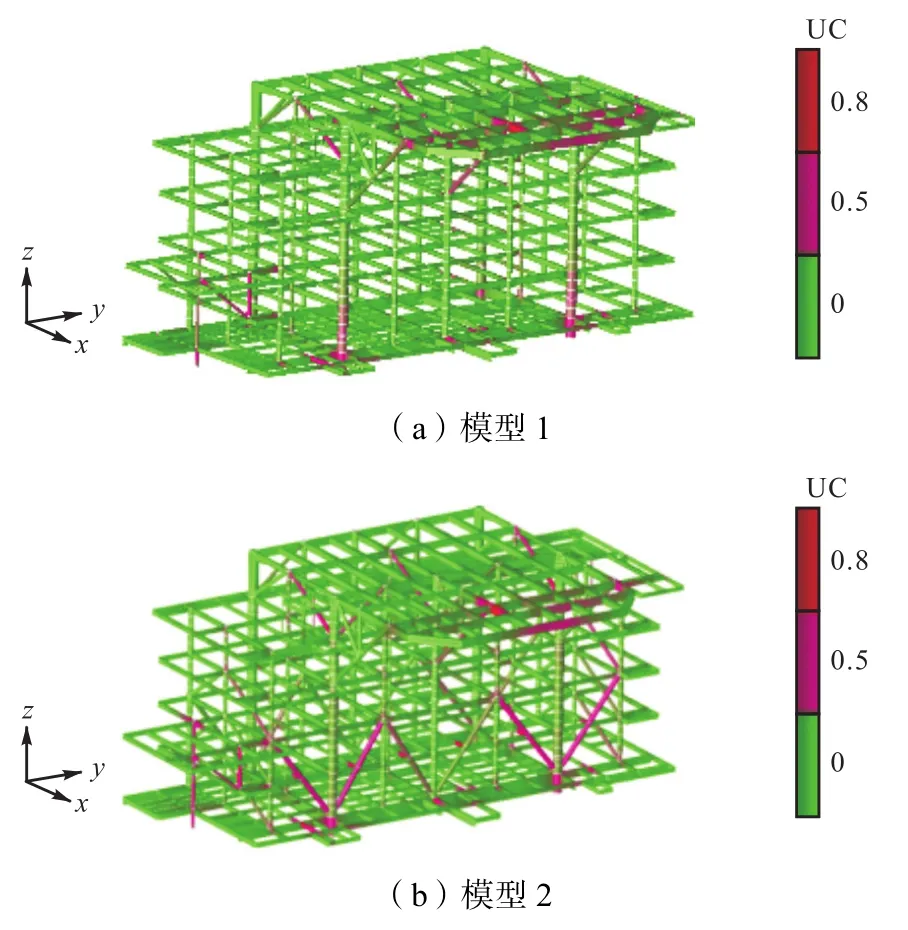
图8 杆件应力分布示意Fig.8 Stress distribution diagram of members in living quarter

由图8可知，两种模型应力分布状态存在明显差异，这是由于其结构形式不同，改变了载荷传递路径，其中，模型 2应力主要集中于垂向斜撑上，说明垂向斜撑为主要传力构件；模型1应力主要集中于生活楼底层主立柱根部，说明取消斜撑后，主立柱成为主要传力构件.由此可知，正是由于这一传递路径的变化，使得模型 1的 4个主立柱根部(C8)以及与主立柱相连的底层甲板主梁(H4)的 UC值较模型 2有所增加，即该区域会出现较明显的应力集中现象，因此，生活楼取消斜撑时，应重点关注该区域的构件.

进一步分析生活楼取消斜撑后的波纹板强度，计算模型1四周侧壁波纹板所有工况下的最大强度UC值，结果均小于 1，说明生活楼取消斜撑后其侧壁波纹板结构亦满足强度要求.

提取最大UC值所在工况下波纹板应力分布图，结果如图9所示.

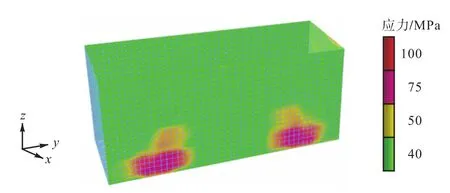
图9 波纹板应力分布Fig.9 Stress distribution of corrugated panels in living quarter

由图9可知，波纹板应力分布具有明显的区域特性，仅在L3和 L1波纹板与主立柱根部相连位置的应力水平较高，存在较为明显的应力集中现象，而远离该区域的应力水平明显下降，大部分波纹板应力水平均在 40,MPa以下.其原因同上，由传力路径改变而致，在此不再赘述.

4 结 论

本文综合对比分析了波纹板和垂向斜撑对导管架平台生活楼结构的强度和刚度贡献，得出结论如下：

(1) 提出生活楼取消斜撑的结构设计方案，该方案不仅能满足规范设计要求，而且波纹板对生活楼框架有着比斜撑更优的刚度和强度贡献，且对于危险工况而言，其贡献度更加明显，从结构刚度、强度和波纹板强度3方面验证了生活楼取消斜撑的可行性.

(2) 生活楼取消斜撑后，考虑波纹板承载，在采用SACS建立波纹板结构时，本文推荐采用近似一个波纹长度的正方形网格尺寸对波纹板进行模拟，以满足工程计算效率和建模精度.(3) 结构取消斜撑后，生活楼靠波纹板与主立柱和甲板梁联合承载，高应力区域转变为生活楼底层主立柱根部，且该位置处波纹板应力水平亦较高，是生活楼采用取消斜撑设计时应重点关注的区域.

：

［1］ 王 胜，席时春，侯晓蕊. 板架结构生活楼的技术与应用[C]//2010全国钢结构学术年会. 北京，中国，2010：291-296.Wang Sheng，Xi Shichun，Hou Xiaorui. Technique and application of grillage living quarter [C]//2010the National Steel Construction Academic Essays. Beijing，China，2010：291-296.

［2］ 李利飞，徐田甜，张建勇. 浅谈我国海上固定式平台生活模块的现状和发展趋势[J]. 船海工程，2008，37(3)：87-91.Li Lifei，Xu Tiantian，Zhang Jianyong. The status quo and development trend of the living quarters for fixed offshore platform in China[J].Ship & Ocean Engineering，2008，37(3)：87-91(in Chinese).

［3］ 康思伟，朱本瑞，李润野. 平台生活楼适应 SPMT运输的结构设计[J]. 天然气与石油，2017，35(1)：119-124.Kang Siwei，Zhu Benrui，Li Runye. SPMT transportation structural design for platform living quarter[J].Natural Gas and Oil，2017，35(1)：119-124(in Chinese).

［4］ 苏新福，曹志强，徐 青，等. 海上固定平台生活楼的设计[J]. 中国造船，2007，48(增刊)：253-260.Su Xinfu，Cao Zhiqiang，Xu Qing，et al. Living quarter design of offshore fixed platform[J].Shipbuilding of China，2007，48(Suppl)：253-260(in Chinese).

［5］ 宋 杰，许 莲，李春萌. 海上固定平台生活楼模块舾装减重影响因素分析与建议[J]. 海洋工程装备与技术，2016，1(3)：207-212.Song Jie，Xu Lian，Li Chunmeng. Analysis and advice on impact factors of outfitting weight reduction for offshore fixed platform living quarters module[J].Ocean Engineering Equipment and Technology，2016，1(3)：207-212(in Chinese).

［6］ Nilson A H，Ammar A R. Finite element analysis of metal deck shear diaphragms[J].Journal of the Structural Division，1974，100(4)：711-726.

［7］ 郭彦林，张庆林. 波折腹板工形构件截面承载力设计方法[J]. 建筑科学与工程学报，2006，23(4)：58-63.Guo Yanlin，Zhang Qinglin. Design method of section bearing capacity of I-type member of corrugated web[J].Journal of Architecture and Civil Engineering，2006，23(4)：58-63(in Chinese).

［8］ 李靓姣. 波浪形钢板墙的受力性能及设计方法研究[D]. 北京：清华大学土木工程系，2012.Li Liangjiao. Research on Behavior and Design Methods of Sinusoidal Steel Plate Wall[D]. Beijing：Department of Civil Engineering，Tsinghua University，2012(in Chinese).

［9］ Kheirikhah M M，Babaghasabha V. Bending and buckling analysis of corrugated composite sandwich plates[J].Journal of the Brazilian Society of Mechanical Sciences & Engineering，2016，38(8)：1-18.

［10］ Farzampour A，Laman J A，Mofid M. Behavior prediction of corrugated steel plate shear walls with openings[J].Journal of Constructional Steel Research，2015，114(8)：258-268.

［11］ 陶 旭. 导管架平台生活楼波纹板承载力数值模拟研究[D]. 天津：天津大学建筑工程学院，2017.Tao Xu. Numerical Studies on Bearing Capacity of Corrugated Plateused in Living Quarter for Jackets[D].Tianjin：School of Civil Engineering，Tianjin University，2017(in Chinese).

［12］ 李润野. 导管架生活楼组块 SPMT装船过程分析研究[D]. 天津：天津大学建筑工程学院，2017.Li Runye. SPMT Support Analysis of Jacket Living Quarter Transportation[D]. Tianjin：School of Civil Engineering，Tianjin University，2017(in Chinese).

［13］ Ji Huidi，Cui Weicheng，Zhang Shengkun. Ultimate strength analysis of corrugated bulkheads considering influence of shear force and adjoining structures[J].Journal of Constructional Steel Research，2001，57(5)：525-545.

［14］ Paik J K，Seo J K. Nonlinear finite element method models for ultimate strength analysis of steel stiffenedplate structures under combined biaxial compression and lateral pressure actions—Part I：Plate elements[J].Thin-Walled Structures，2009，47(8)：1008-1017.

［15］ American Petroleum Institute. RP 2A-WSD Recommended Practice for Planning，Designing and Constructing Fixed Offshore Platforms：Working Stress Design[S]. Washington DC：API Publishing Services，2012.

［16］ Det Norske Veritas. RU-SHIP DNV Rules for Classification of Ships[S]. Norway：Det Norske Veritas，2015.