用MTF－QNN模型预测水中溶解氧含量

贾花萍

（渭南师范学院网络安全与信息化学院，陕西渭南714099）

水中溶解氧（dissolved oxygen，简称DO）指溶解在水中的氧，溶解氧以分子状态存在于水中，用1 L水里氧气的毫克数来表示。水中溶解氧含量的多少是衡量水体自净能力的一个指标。水体自净在静止的水中进行得较为缓慢，在循环的水中进行得较为充分。水中的含氧量和水温有密切关系，水温越高，水分子活动得越快；水温越低，水分子活动得越慢。当温度低时，氧气滞留在水中的时间就长；当温度高时，氧气滞留在水中的时间就短。水中溶解氧的含量与气压、水温、压强等都有相应的关系。水中溶解氧在淡水生态系统和水环境生物地球化学循环中具有重要意义。溶解氧是维持水体生态环境动态平衡的重要环境因子，同时是维持水生生物生存的必备条件，且可参与部分物质转化［1］。溶解氧作为水质的一项重要参数，在工厂化水产养殖中具有重要作用［2－3］。因此，对水中溶解氧含量进行预测至关重要。

影响水中溶解氧含量的各因素关系复杂，很难进行数学建模，水中溶解氧预测模型是一个复杂的非线性系统。传统的水中溶解氧预测模型主要根据经验公式进行估算，或通过简单的试验进行拟合，这2种方法所建立的模型不具备普遍适用性。针对水中溶解氧预测问题，国内外学者作了大量的研究，其中支持向量机在预测中的应用较为广泛。刘双印等提出基于时间序列相似数据的最小二乘支持向量机（least squares support vector regression，简称LSSVR）的水中溶解氧在线预测模型，该模型具有较好的综合预测性能［4］。朱成云等提出混沌变异的分布估计（chaotic mutation estimation of distribution algorithm，简称CMEDA）算法优化最小二乘支持向量机模型（LSSVR）来预测江苏省扬中市红鲷鱼工厂化养殖鱼塘的水中溶解氧含量，通过对4种模型的预测精度进行对比分析发现，该方法在预测水中溶解氧含量时的预测精度较高［5］。支持向量机预测方法具有计算效率高、泛化性能强等特点，但所需存储空间和计算量会随着时间序列的获取或在线采集样本数的增加而增大，易产生数据过饱和、泛化能力差甚至模型性能失效等问题［6－7］。

传统的神经网络由于具有较强的非线性问题处理能力而被广泛应用于水中溶解氧含量预测的研究［8－10］，如动态神经网络方法［11－12］可以动态更新与在线预测水中溶解氧含量，但该方法的计算复杂度高，且不适合对在线更新速度较快的时间序列进行预测。韩广等针对污水处理过程水中溶解氧浓度的控制问题提出采用前馈神经网络（feedforward neural network modeling and control，简称FNNMC）对水中溶解氧浓度进行建模控制，该方法对水中溶解氧浓度的控制具有良好的建模能力、更高的精度及更好的动态响应能力［13］。欧红香等提出采用改进的数据处理组（groupmethod of data handling，简称GMDH）方法对长良川地区水中溶解氧进行长期预测，预测模型基本满足模型相关度较高的要求，模型的相关度可达到0.96［14］。但神经网络存在的收敛速度慢、容易陷入局部极小值等缺点可影响预测的精确性和稳定性。为此，苏彩红等提出一种人工蜂群算法（artificial bee colony，简称ABC）与BP（back propagation）神经网络融合的水中溶解氧预测模型；仿真结果表明，ABC－BP算法的预测精度更高，误差更稳定［15］。缪新颖等提出（levenberg－marquardt，简称 LM）神经网络和遗传算法（genetic algorithm，简称GA）的水中溶解氧预测模型GA－LM，该模型预测的溶解氧值和实际测定值的吻合度较好，预测更为精准，运行时间明显减少［16］。郭连喜等提出快速粒子群优化算法对模糊神经网络进行训练，收敛速度明显加快［17］。

本研究拟采用多层激励函数的量子神经网络（modulation transfer function－quantum neural network，简称MTF－QNN）建立水中溶解氧含量预测模型，但由于神经网络为前馈型网络及沿梯度下降的算法，在进行网络训练时有陷入局部极小的可能，针对这一缺陷，提出一种可以使量子神经网络逃离局部极小点的算法，并将其应用到量子神经网络中进行网络误差调整。为证明该方法的预测精度，分别采用多层激励函数的量子神经网络与传统BP神经网络对水中溶解氧含量进行预测，并对预测结果进行对比。

1 材料与方法

影响水中溶解氧含量的因素比较复杂，包括生物、物理、化学等多个方面，主要影响因素有水体温度、水体中的含氮量和空气中氧气组分的分压力等［18－21］。另外，池塘中氧气的来源与消耗、氧气的溶解与溢出速率等也是水中溶解氧含量的重要影响因素。针对某一具体池塘来说，水中溶解氧含量与不同季节、测量时间、测量点的位置和深度、风速以及池塘的深度和表面积有关。本研究通过综合分析并考虑各变量的可测性，选取池塘水体温度、亚硝酸盐、氨氮值以及总氮值等4个变量作为样本数据。

以陕西渭南某地区的池塘水质作为数据来源进行研究，由于池塘的水中溶解氧含量和季节有关，收集该池塘近3年在同一个季节的数据300组，并选取260组覆盖面比较大的数据作为建模数据，其中240组数据作为训练数据来训练网络，20组数据作为测试数据对网络模型进行检验，用于检验的20组数据如表1所示。

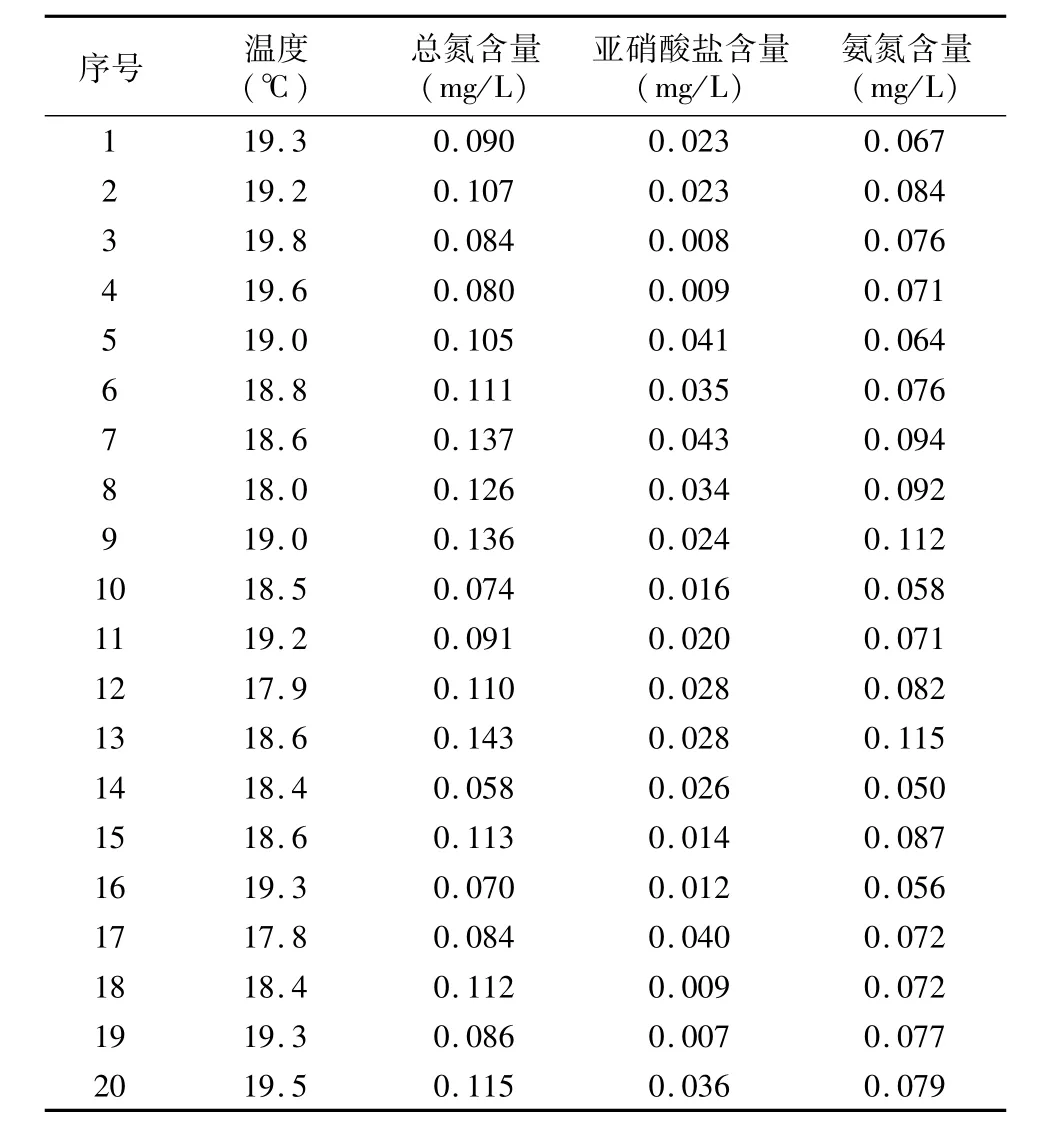
表1 测试样本

1.1 数据归一化预处理

数据归一化处理是数据挖掘的一项基础工作，指将要处理的数据通过某种算法限制在一定范围内，目的是为了方便数据处理及保证加快程序运行时的收敛速度。由于不同评价指标往往具有不同的量纲和量纲单位，这样会影响到数据的预测精度，为消除指标之间的量纲影响，须要进行数据标准化处理，以解决数据指标之间的可比性问题。原始样本数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。

数据归一化方法有2种，一种是把有量纲表达式变为无量纲表达式；一种是把数据变为［0，1］之间的小数，这种方法主要是为了数据处理方便。

1.1.1 Z－score标准化方法 该方法将原始数据的均值（mean）和标准差（standard deviation）进行数据标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1，转化函数为

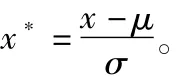
式中：μ为所有样本数据的均值；σ为所有样本数据的标准差；x表示标准化后的样本数据；x表示标准化前的样本数据。

1.1.2 min－max标准化方法 min－max（min－max normalization）标准化也称为离差标准化，指通过对原始数据进行线性变换使结果值映射到［0，1］之间。标准化公式为

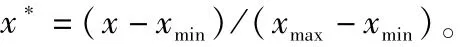
式中：xmax表示样本数据的最大值；xmin表示样本数据的最小值。这种方法的缺陷就是当有新数据加入时，可能导致xmax和xmin的变化，须要重新进行定义。

本研究数据归一化方法采用的是min－max标准化方法。对选取的240组数据进行归一化处理，然后对网络进行训练得出网络模型，再用20组数据进行模型测试，测试样本归一化后的数据如表2所示。

表2 归一化后的数据

1.2 BP神经网络预测模型

BP网络于1986年由以Rumelhart和McCelland为首的科学家小组提出［22］，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量输入－输出模式的映射关系，而无需事前揭示描述这种映射关系的数学方程。但由于学习速率固定，因此网络的收敛速度慢，需要较长的训练时间。BP算法可以使权值收敛到某个值，但不能保证其为误差平面的全局最小值，这是因为BP算法采用梯度下降算法可能会产生一个局部最小值。BP算法网络隐含层的层数和单元数的选择是根据经验或者通过反复试验确定的，因此，网络往往存在很大的冗余性，在一定程度上增加了网络学习的负担。

在对水中溶解氧含量进行预测时，根据BP神经网络原理，采用单隐含层的网络结构。多隐含层的网络结构虽然精度高，误差低，但神经网络的复杂度和训练时间会增加。BP神经网络中的输入参数为4个，即输入层的输入单元为4个（表1中的温度、总氮含量、亚硝酸盐含量、氨氮含量）。输出层为预测的水中溶解氧浓度，故输出层的个数为1，即输出层单元个数为1。中间层隐含层节点的个数（隐含层节点单元数）根据Kolmogorov定理计算，即

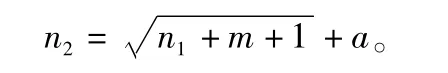
式中：a的值为1到10；n2表示隐含层节点数目；n1表示输入层数目；m表示输出层数目。取a为5，经计算得n2为8。传递函数为“S”形正切函数tansig。

1.3 多层激励函数的量子神经网络预测模型

Benioff等于 1982年提出量子计算概念［23－24］，Kak于1995年将量子理论与神经计算相结合，提出量子神经计算的概念［25－26］，使得量子神经网络受到了广泛关注。同年Chrisley提出量子学习的概念以及非叠加态的量子神经网络模型［27］。Narayanan等探讨了将量子计算引入人工神经网络，并证实量子神经网络在分类方面比传统神经网络更加有效，且不存在收敛速度慢、易陷入局部极小值的缺点［28］。有专家学者已经将量子神经网络应用到电网故障诊断［29］、心电图识别［30］、指纹识别技术［31］等领域并取得了很好的研究成果。

Karayiannis等提出基于多层激励函数的量子神经网络模型［32］。量子神经网络隐含层神经元的激励函数是多个Sigmoid函数的线性叠加，被称之为多层激励函数［33］。多层激励函数隐含层节点的输入输出函数为：

式中：f为f（x）＝；β表示陡度因子（斜率）；n表示量s子层数；s表示量子间隔数目（s＝1，2，…，n）；θs表示量子间隔；X表示网络输入向量；W表示网络权向量；θs和WTX（量子神经元的输入激励）参数未知。

若量子神经网络输入层单元个数是n，输出层单元个数为m0，每个隐含层神经元个数为m，则隐含层第j个单元的输入为

式中：wi，j表示输入层第i个单元与隐含层第j个单元的连接权值；xi，k表示输入层第i个单元对应的输出值，则输出为

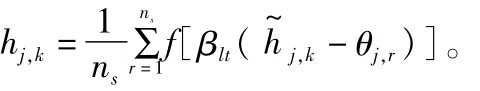
式中：βlt表示斜率因子；f为 sigmoid函数；θj，r表示量子间隔。

第k个输入向量对应的输出层的输入为

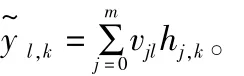
式中：vjl表示隐含层第j个单元与输出层第l个单元的连接权值。对应的输出层的输出为

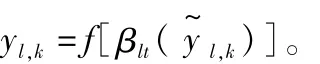
量子神经网络的学习过程分2步：

（1）对网络联结权值进行调整，使输入样本数据和特征空间相对应，权值的调整算法采用误差梯度下降法，该方法与BP神经网络权值调整方法一样；网络的误差函数是：

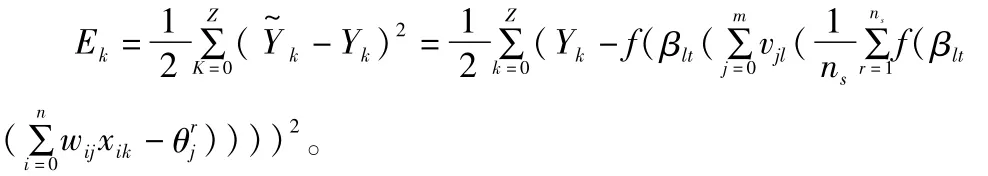
式中：Ek表示网络实际输出值和期望输出值的差值表示网络期望输出值；Yk表示网络实际输出值；wij表示输入层和隐含层的连接权值；vjl表示隐含层与输出层的连接权值k表示对于第k个输入向量，第s个单元的输出；、Δwij表示输出层权值和隐含层权值的调整量。误差函数的调整按照权值的调整进行，输出层权值的调整公式为

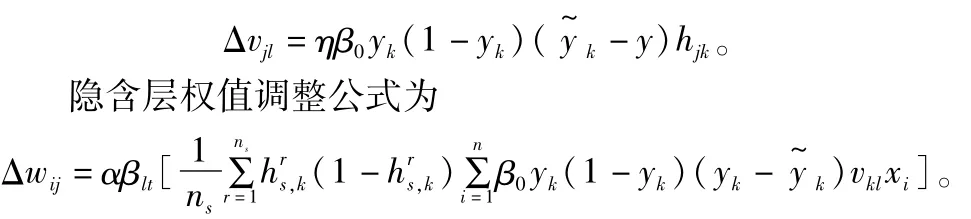
（2）对隐含层神经元的量子间隔进行调整，其算法与权值调整算法一致，采用梯度下降算法，得到样本数据中的不确定性。

对于第m个类cm的所有样本可以计算隐含层第j个单元的输出，公式如下：

其中，αθ表示学习率。

传统的BP神经网络不设置量子间隔，即用于预测的数据类在每个预测处的间隔相等。而多层激励函数的量子神经网络在预测处的量子间隔值不同，量子间隔为θsj。可以看出，量子间隔不相等，量子间隔的增加能够解决BP神经网络在预测水中溶解氧含量时数据样本混淆的问题。量子神经网络为前馈型网络及沿梯度下降的算法，在进行网络训练时有陷入局部极小的可能，针对这一缺陷，提出一种可以使量子神经网络逃离局部极小点的算法，并将其用到量子神经网络中进行网络误差调整。算法如下：若｜Ek－Ek－1｜＜0.000 000 1，其中，Ek、Ek－1是连续进行2次迭代后的误差，当 Ek＞目标误差时，量子神经网络会陷入局部极小点，如果网络陷入局部极小点，则使｜Ek－Ek－1｜＝Y×｜Ek－Ek－1｜，其中 Y为冲量值，如果量子神经网络没有陷入局部极小，则Y＝1，按照量子神经网络算法训练数据。当其陷入局部极小时，取Y＞1，使神经网络在梯度上出现大的跳跃。如果｜Ek－Emin｜＜0.000 001，其中Emin是上次局部极小点的值，则量子神经网络没有逃离上次的局部极小，令c＝c＋1，Y＝1＋Y×f（c－1），其中，f是陷入同一局部极小点次数的函数，c是陷入同一局部极小点的次数，1是冲量值的增量，且 f（0）＝0。

量子神经网络应用于水中溶解氧含量预测时首先要进行训练，也就是量子神经网络的学习过程。选取240组数据作为训练数据进行网络训练，使网络训练误差达到目标要求，并将得到的训练好的神经网络以权值的形式存储。测试样本时，用训练好的权值和阈值进行预测，得到水中溶解氧含量预测结果。在创建多层激励的量子神经网络时，其初始化参数的选取如下。

1.3.1 初始权值的选取 量子神经网络初始权值一般选［－1，1］之间的随机数。初始权值的选取与网络结构及节点输入的取值有关，并且对网络学习收敛速度的影响较大。因此，初始权值的选取非常重要。如果对样本输入单元进行归一化处理，使其取值范围在［0，1］，那么，初始权值的选取就只与网络结构有关。量子神经网络根据经验训练的初始权值取 ±e－0.1槡n，其中，n为输入层神经单元节点个数。

1.3.2 输入层、输出层单元个数、隐含层数目及隐含层单元个数的选取 多层激励函数的量子神经网络在预测水中溶解氧含量时的输入层单元为4个，即表1中的温度、总氮含量、亚硝酸盐含量、氨氮含量。输出层为预测的水中溶解氧含量，故输出层单元为1个。隐含层越多，分类能力越强，但量子神经网络结构也越复杂，收敛性能较差，且容易陷入局部最小。因此，隐含层取1～2层时收敛性较好，在预测水中溶解氧含量时，取隐含层数目为1层。隐含层节点个数选择较多时，误差较小，训练时间较长，且收敛速度变慢，从而降低神经网络泛化能力。隐含层节点个数较少时，网络不能很好地获取样本数据规律，因此，预测及分类能力较差。对水中溶解氧含量进行预测时，可根据经验公式 Kolmogorov定理计算，即m＝＋a，其中a的值为1到10；m表示隐含层节点数目；n表示输入层数目；m0表示输出层数目；在实际预测时，根据经验确定隐含层神经元个数m为8。

1.3.3 学习率的调整 学习率选择不当会使量子神经网络算法的收敛速度变慢。学习率选择过小，网络收敛速度变慢；学习率选择过大，可以尽快逼近误差函数极小值，但会导致振荡甚至发散。在预测水中溶解氧含量时，可以采用自适应调整学习率的方式来优化神经网络，即下降太慢时，可使步长增加，下降太快时，可使步长减小。

1.3.4 训练方法 预测水中溶解氧含量的多层激励量子神经网络的隐含层采用多个sigmoid函数的叠加，输出层函数也采用sigmoid函数。设定量子神经网络预测模型的网络输入节点个数为4，隐含层激励函数使用2个sigmoid函数叠加，隐含层节点个数根据经验设为8，输出单元节点个数为1。系统精度设置为1×10－6，斜率因子为1，步长为 0.001。其中240组数据用于网络训练，20组数据用于测试。

2 结果与分析

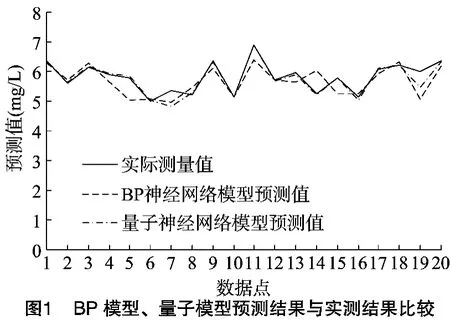
采用传统BP神经网络模型与多层激励函数的量子神经网络模型对陕西渭南某地区池塘水质的水中溶解氧含量进行预测，采用Matlab软件进行预测，预测结果如表3所示，结果对比曲线如图1所示。

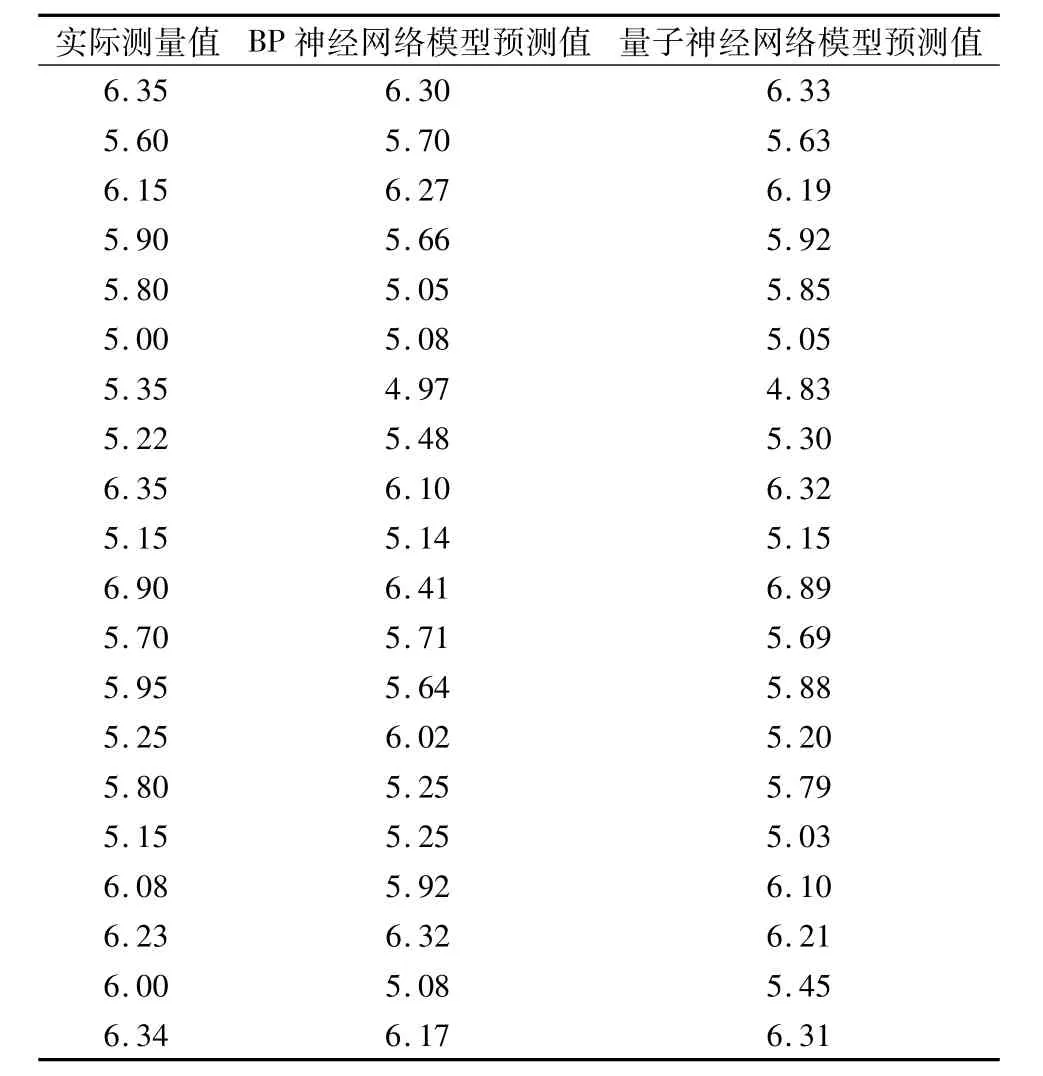
表3 BP模型、量子模型对水中溶解氧含量的预测结果与实测结果比较 mg／L

由表3可以看出，在用于进行测试的20组数据中，多层激励函数的量子神经网络预测的水中溶解氧含量与实际测量得到的水中溶解氧含量之差的绝对值小于0.5 mg／L的为18组，占90%；而采用传统BP神经网络预测的水中溶解氧含量与实际测量得到的水中溶解氧之差的绝对值小于0.5 mg／L的为16组，占80%。

由图1也可以看出，多层激励函数的量子神经网络模型在预测水中溶解氧含量时与实际测量结果曲线拟合较好，传统BP神经网络预测的水中溶解氧含量与实际测量水中溶解氧含量曲线在第5、7、11、14、15、19组数据处拟合效果较差。可见，采用多层激励函数的量子神经网络模型预测水中溶解氧含量的泛化能力较强。由此可见，采用多层激励函数的量子神经网络模型预测水中溶解氧含量的方法是可行的，且本研究所建立的量子神经网络模型具有较高的预测精度。

3 讨论与结论

由于影响水中溶解氧含量的因素比较复杂，针对传统神经网络在训练时有可能陷入局部极小的缺陷，采用多层激励函数的量子神经网络建立水中溶解氧含量预测模型。

通过对水中溶解氧含量的预测结果可以看出，该模型较传统的神经网络方法来说，预测结果更加精确，网络泛化能力较强；分析了前馈型神经网络易陷于局部极小的原因，提出一种解决方法，并辅助量子神经网络有效地解决了它易陷入局部极小的缺陷，将该算法应用到量子神经网络中进行网络误差调整；针对水中溶解氧含量数据样本性质，完成了量子神经网络的算法设计与实现，包含权值的调整和量子间隔的实现，分析了量子神经网络较传统神经网络在预测方面的优越性。

本研究将多层激励函数的量子神经网络（MTF－QNN）应用于水溶解氧含量的预测，取得了较好的预测效果，从中可以得出，将该方法应用于其他预测问题或分类问题中也将会取得意想不到的效果。

参考文献：

［1］王嘉学，刘丛强，王锐良.滇池及入湖河道富营养化治理的人工辅助增氧［J］.地球与环境，2008，36（2）：183－187.

［2］杨 斌，翟雪梅，王 强.长江河口南支水域溶解氧动力学模型的应用［J］.中国海洋大学学报（自然科学版），2004，34（2）：253－260.

［3］邹志红，王学良.BP模型在河流水质预测中的误差分析［J］.环境科学学报，2007，27（6）：1038－1042.

［4］刘双印，徐龙琴，李道亮，等.基于时间相似数据的支持向量机水质溶解氧在线预测［J］.农业工程学报，2014，30（3）：155－162.

［5］朱成云，刘星桥，李 慧，等.工厂化水产养殖溶解氧预测模型优化［J］.农业机械学报，2016，47（1）：273－278.

［6］张浩然，汪晓东.回归最小二乘支持向量机的增量和在线式学习算法［J］.计算机学报，2006，29（3）：400－406.

［7］Zhao Y P，Sun JG，Du Z H，et al.Online independent reduced least squares support vector regression［J］.Information Sciences，2012，201：37－52.

［8］白建东，叶德谦，李春兴.混沌时间序列的Volterra级数多步预测研究［J］.计算机仿真，2008，25（6）：274－276，280.

［9］陆振波，蔡志明，姜可宇.基于稀疏Volterra滤波器混沌时间序列自适应预测［J］.系统工程与电子技术，2007，29（9）：1428－1431.

［10］Farmer J D，Sidorowich J J.Predicting chaotic time series［J］.Physical Review Letters，1987，59（8）：845－848.

［11］Vairappan C，Tamura H，Gao S C，et al.Batch type local searchbased adaptive neuro－fuzzy inference system（ANFIS）with selffeedbacks for time－series prediction［J］.Neurocomputing，2009，72（7）：1870－1877.

［12］Chen Y M，Lin C T.Dynamic parameter optimization of evolutionary computation for on－line prediction of time series with changing dynamics［J］.Applied Soft Computing，2007，7（4）：1170－1176.

［13］韩 广，乔俊飞，薄迎春.溶解氧浓度的前馈神经网络建模控制方法［J］.控制理论与应用，2013，30（5）：585－591.

［14］欧红香，郑 铭，田中雅史.长良川水质中溶解氧和化学耗氧量预测模型的建立［J］.四川环境，2003，22（3）：91－94.

［15］苏彩红，向 娜，林梅金.基于ABC优化算法的神经网络水溶解氧预测［J］.计算机仿真，2013，30（11）：325－329.

［16］缪新颖，葛廷友，高，等.基于神经网络和遗传算法的池塘溶解氧预测模型［J］.大连海洋大学学报，2011，26（3）：264－267.

［17］郭连喜，邓长辉.基于模糊神经网络的池塘溶解氧预测模型［J］.水产学报，2006，30（2）：225－229.

［18］雷衍之.养殖水环境化学［M］.北京：中国农业出版社，2004：63－89.

［19］徐 宁，李德尚，董双林.海水养殖池塘溶氧平衡的实验研究［J］.中国水产科学，1999，6（1）：69－74.

［20］臧维玲，戴习林，朱正国，等.中国对虾池溶解氧的收支平衡状态［J］.海洋通报，1995，17（4）：137－141.

［21］方志山，杨圣云，许振祖.杏林虾池综合养殖系统主要环境因子的变化［J］.台湾海峡，2001，20（4）：496－501.

［22］朱大奇，史 慧.人工神经网络原理及应用［M］.北京：科学出版社，2006：26－28.

［23］Benioff P A.Quantum mechanical hamiltonian model of turing machine［J］.Journal of Statistical Physics，1982，29（3）：515－546.

［24］Feynman R P.Simulating physics with computers［J］.International Journal of Theoretical Physics，1982，21（6／7）：467－488.

［25］Kak S.Quantum neural computing［J］.Information Science，1995，83：143－160.

［26］Kak S.Quantum neural computing［J］.Advances in Imaging and Electron Physics，1995，94：259－313.

［27］Chrisley R.Quantum learning［C］／／Finish Association of Artificial Intelligence.Lapland，2005：77－89

［28］Narayanan A，Menneer T. Quantum artifical neural network architectures and components［J］.Information Sciences，2000，128（3／4）：231－255.

［29］刘 超.基于粗糙集理论和量子神经网络的电网故障诊断方法研究［D］.成都：西南交通大学，2008.

［30］柳 丹.量子神经网络模型及其在心电图分类识别中的应用研究［D］.南京：南京邮电大学，2012.

［31］李茶茶.基于量子神经网络的指纹识别技术研究［D］.南京：南京邮电大学，2011.

［32］Karayiannis N B，Purushotaman G.Fuzzy pattern classification using feedforward neural networks with multilevel hidden neurons［J］.IEEE Transaction on Neural Network，1994，5（1）：127－132.

［33］周树德，王 岩，孙增圻，等.量子神经网络［M］.香港：香港中文大学出版社，2003.