基于通行异常行为的高速公路车辆信用度评价模型与算法研究

陈尔希，曾献辉，胡征

（1.东华大学 信息科学技术学院，上海 201620；2.数字化纺织服装技术教育部工程研究中心，上海 201620）

0 引言

随着高速公路联网规模的不断扩大，行车距离越来越远，对通过路网的车辆（尤其货车等重载车辆）单次收费金额也越来越大，随之而来的是利用各种作弊手段[1-6]逃费的车辆数的增加，因此逃费稽查越来越受到高速公路稽查部门的重视。目前，稽查部门主要以人工审核的方式综合分析高速公路收费后台数据，从而查获逃费车辆。这种工作模式效率极为低下，漏判、误判重要逃费线索数据时有发生。为了充分挖掘通行数据中的信息价值，提高稽查部门的工作效率，高速公路管理部门迫切需要利用新技术来提升逃费稽查水平。

目前，国际上有关防逃费方面的研究有：Delbosc等[7]采用聚类分析法对逃费行为展开研究；Guarda等[8]、Troncoso等[9]针对高频的公交逃费问题，通过负二项式回归模型发现了导致逃费率增加的几个关键因素，并提出规避逃费问题的五种方法；Jankowski[10]利用博弈论对逃费的动机进行了分析，并指出不同博弈参与者的利益动机，同时从博弈角度给出了一些防逃费建议。在国内，关于防逃费的研究主要有：刁洪祥等[11-14]，刘勇等[15]采用聚类分析法、决策树和神经网络算法对联网收费数据进行建模和分析逃费车辆，并提出了部分防逃费措施，但其研究基本停留在理论阶段，尚未应用到逃费稽查中；赵彦等[16]采用聚类分析、判别分析和逻辑回归分析相结合的方法，构建了通行卡逃费行为预测模型，但该模型对非超时逃费行为的识别能力不足；张晓航[17]提出使用数据挖掘工具WEAK实现对车牌不符、变档等部分逃费行为的稽查。从实际应用来看，这些方法存在数据收集困难、准确性较低、实际应用难度高等问题。

随着高速公路大数据系统的形成，如何直接从车辆通行数据中挖掘出逃费车辆，对逃费稽查的实际应用具有重要意义。为此，笔者将基于浙江省某高速公路近三年的通行历史数据，结合稽查部门的逃费车辆历史记录，分析逃费行为发生时可能出现的各种异常通行行为，提出用于评判车辆逃费可疑程度的车辆通行信用度评价指标，给出计算该指标的多属性效用模型，并利用BP神经网络算法对该模型进行改进，最后对结果的适用性和准确度加以验证。

1 车辆通行异常行为分析

高速公路通行费计算方法是根据车辆在高速公路的出入信息和路径信息，查找对应车型在所经过路段的基本费额，考虑车辆重量等因素，分别乘以对应的通行里程，最后汇总相加得出该车通行的总费额。据此，车辆可能通过缩短里程或改变车型两种方式实现通行费的偷逃。通过对稽查过程调研和已有偷逃车辆通行数据的分析，现归纳出11种典型的车辆通行异常行为，如表1所示。

表1 车辆逃费时可能出现的异常行为

以上11种异常行为对判断车辆是否存在逃费行为提供了非常有价值的依据，异常出现次数越多，逃费的可能性就越大。基于此，本文将逃费稽查看作一个考虑多个评价属性的决策性问题，构建以11种异常出现次数为评价属性的车辆信用度评价模型。利用该模型计算得到每辆车的信用度值，并据此判断车辆逃费可疑度的大小，即信用度值越小，则出现逃费行为的可能性就越大。在实际应用时，可考虑将信用值较小的车辆提供给稽查部门，从而提升人工稽查的效率和准确度。

2 基于多属性效用模型的车辆信用度评价

2.1 车辆信用度

为了有效地甄别最有可能偷逃通行费的车辆，本文提出对每一辆车建立信用度的概念。该信用度仅用于对车辆在高速公路通行中出现各种异常情况的度量。信用度的取值范围为0～100分，其中100分为信用度满分，表示基本未出现过异常；0分是最差值，表示所有类别的异常出现次数都最多。车辆初始信用度值均为100分，根据出现异常的类别及次数，该值将逐步降低。

2.2 车辆信用度计算

以车辆信用度作为衡量车辆逃费可疑程度的量化指标，其计算可以看作是一个基于车辆异常行为出现次数的多属性效用模型的决策问题，即考虑车辆的11种异常行为出现次数及其重要程度，通过某种计算模型，得到定量的综合评估值。本文采用基于加权平均的多属性效用模型进行车辆信用度计算，具体采用扣分的方式进行。首先，计算各类异常下每辆车的扣分情况，异常越多，扣分越多，最多扣100分；然后，将所有异常类型的扣分进行加权平均，得到对应车辆的总扣分；最后，用100分减去总扣分，即得到车辆的最终信用度值，计算方法为：

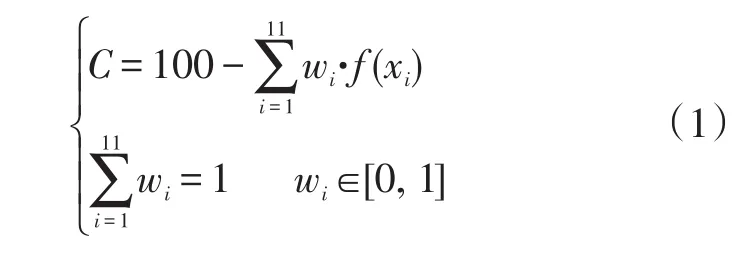
式（1）中：C为车辆信用度（分）；wi为第i类异常的权重值；xi为第i类异常出现的次数（次）；f(xi)为第i类异常出现次数的效用函数。

2.3 信用度评价模型构建

从式（1）可以看出，信用度评价模型的构建可分为两个步骤：

（1）确定每类异常的权值；

（2）确定每类异常出现次数的效用函数。

目前已有很多理论和方法用于确定权值，比如主观赋值法、客观赋值法和机器学习法等。本文通过对稽查人员的问卷调查、统计分析和多次试验，得到相应的权值。鉴于各类异常出现的次数虽然差别很大，但其效用函数基本相同，同时由于信用度的定义区间为[0,100]，而异常次数的取值可能会超过100，故需要对异常出现次数进行预处理，将数据归一化到0～100范围内，否则可能出现信用度值为负的情况，这是没有意义的。

本文效用函数的构建思路是：首先找出各类异常的平均出现次数，然后估计出最大可能出现次数，最后利用归一化处理将效用值统一到0～100之间，具体按下式计算：

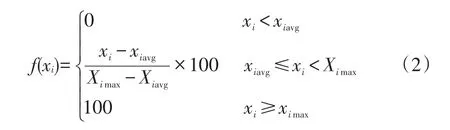
式（2）中：Xiavg为第i类异常的平均次数（次）；Ximax为第i类异常的最大次数（次）；f(xi)与xi的意义同式（1）。

2.4 模型准确率验证

为了验证模型的适用性和有效性，本文基于浙江省某高速公路公司2015—2017年的通行数据，分析得到约3×107辆车的通行异常行为数据，接着利用前文给出的方法计算得出所有车辆的信用度值。部分车辆通行异常行为数据与信用度值如表2所示。表中的异常行为次数是根据高速公路车辆通行流水数据分析所得，比如车辆进出站车牌不一致，根据收费系统中车辆进出站的车牌，对比其相似度，相似度值大于或等于某个设定值，则认为车牌是一致的，否则便不一致，对应类型的异常次数加1。

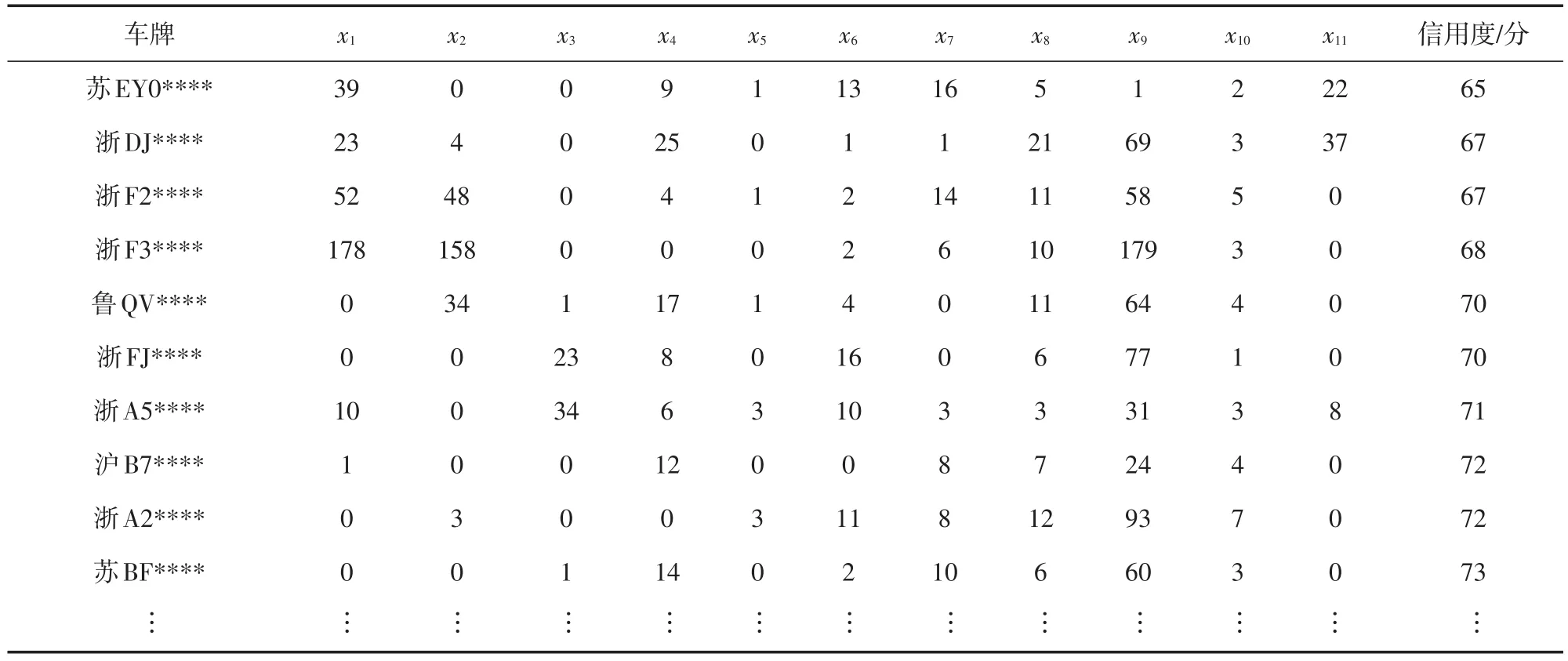
表2 车辆的通行异常行为数据与信用度值

面对海量的车辆数据，不可能对每辆信用度值较低的车辆进行稽查。为了尽快发现有问题的车辆，将信用度最低的200辆车的信息提供给稽查部门进行稽查，最终发现实际存在问题的车辆有30辆，其中19辆车曾被稽查过（新发现的问题车辆为11辆），另外还有35辆车无确凿证据，其余为正常车辆，模型正确率约为33%。可见，所建模型虽然准确率不高，但对逃费稽查工作还是有一定帮助的，可在一定程度上减少人工稽查的工作量，起到辅助稽查的作用。这同时说明本文提出的方法是正确的，也表明车辆通行异常数据与逃费行为之间的确存在一定的对应关系。

分析发现，多属性效用模型正确率不高的原因在于：

（1）线性模型过于简单，无法准确地表示异常行为次数与车辆信用度值之间的关系；

（2）权重值分配不合理，权值的确定存在很大的主观性；

（3）线性效用函数可能不够准确。

为了提高信用度计算的准确度，下面在线性模型的基础上利用BP神经网络的自学习功能对模型进行改进。

3 基于BP神经网络的改进车辆信用度评价模型

BP神经网络是使用最广泛的一种神经网络模型之一，它利用梯度下降算法，使权值沿着误差函数的负梯度方向改变，以期使网络的实际输出与期望输出的均方差最小化。由于BP神经网络算法能够自主学习出一组具有代表性的权值和阈值，且具有良好的非线性逼近能力，故选用BP神经网络算法对多属性效用模型进行改进。BP神经网络的设计主要包括网络层数（主要指隐含层层数）、各层节点数、传递函数、权值等，具体过程如下。

3.1 神经网络结构的确定

BP神经网络通常分输入层、输出层和隐含层，其中隐含层可以为一层或多层。本文选择最典型的三层BP神经网络，即隐含层为一层。BP神经网络的传递函数是Sigmoid函数。

输入层的节点数应等于输入向量的分量数目。本文所建信用度模型的输入量为车辆的11种异常行为特征，故输入层节点数为11。输出层节点则由信用度决定，故确定输出层节点数为1。

虽然增加隐含层层数可以降低网络误差，提高精度，但也会使网络复杂化，延长网络训练时间，甚至出现“过拟合”的倾向，故隐含层节点数的确定对于模型可用性非常关键。根据专家和学者的经验[18]，隐含层节点数Lh可按下式计算：

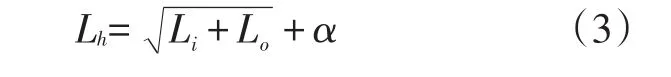
式（3）中：Li和Lo分别为神经网络输入层和输出层的节点数（个）；α为0～10之间的常数。

现取Li=11，Lo=1，经过多次仿真实验发现，当α=3，即隐含层节点数为7时，模型的准确率最高。

综合以上，本文BP神经网络结构确定为：输入层节点数为11，中间层节点数为7，输出层节点数为1，其拓扑结构如图1所示。

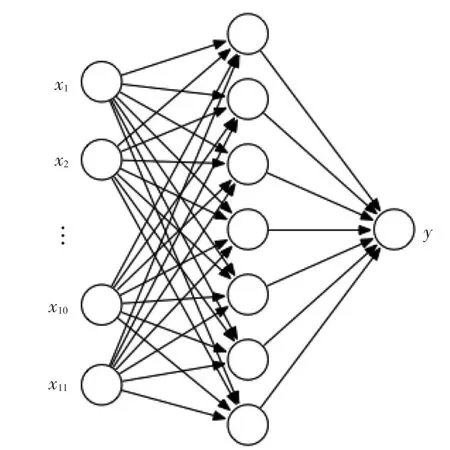
图1 用于计算车辆信用度的BP神经网络拓扑结构

3.2 初始权值的确定

一般情况下，初始权值要足够小才有利于模型的训练。在神经网络中，如果简单地将权值矩阵初始化为零矩阵，将会导致隐含层的每个单元相等。为了让学习更有效率，一般将该矩阵初始化在区间[-ε,ε]内。初始权值按下式计算：

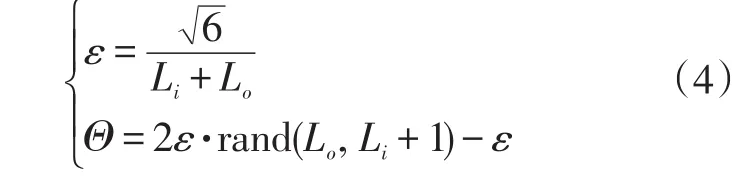
式（4）中：ε是取值为0～1的数；Θ为1×12的权值矩阵，且矩阵中的每个单元取值均在区间[-ε,ε]内；Li和Lo意义同前。

3.3 学习速率的确定

学习速率决定每次训练所产生权值的变化量，过大的学习速率可能导致系统不稳定；否则，又会导致较长的训练时间。为保证系统的稳定性，学习速率通常取值偏小，在0.01～0.7之间，本文取0.01。

4 预测结果分析

为了验证经BP神经网络算法改进后的多属性效用模型的准确率是否有所提升，本文基于多属性效用模型计算出的信用度值，根据人工评价和以往稽查数据对部分样本输出数据加以调整，作为BP神经网络的输入数据进行网络学习。将样本数据的80%作为训练集，10%作为验证集，剩余的10%作为测试集，使用Matlab神经网络工具箱完成模型的建立与仿真。为了找出所训练多个模型中的效果最佳者，使用各个模型对验证集数据进行预测，并记录模型的准确率。接着，采用效果最佳模型所对应的参数来调整模型参数。待模型训练完成后，利用其测试样本中的车辆进行信用度预测。部分测试数据的预测输出和预测误差如图2和图3所示。

图2 模型预测输出与期望输出图

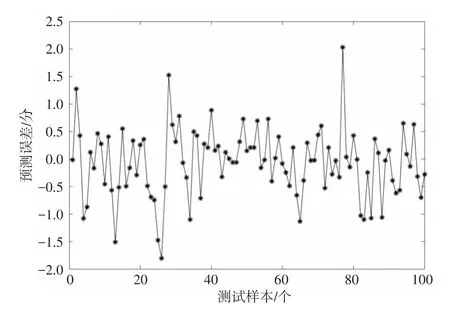
图3 模型信用度预测误差曲线

选取全量数据进行测试，仿真结果显示模型的误差约为3，即该模型预测所得车辆信用度值误差为3分左右，显然该精度能够满足应用要求。

BP神经网络学习完成后，本文对近3×107条车辆通行异常行为数据重新进行计算，得到每辆车新的信用度值。然后，将信用度最低的200辆车提供给稽查部门进行稽查，最终发现实际存在问题的车辆有91辆，其中32辆车曾经已被稽查过（新发现的问题车辆为59辆），另外还有43辆车无确凿证据，其余为正常车辆，整体正确率为67%左右，取得了令人满意的效果。

与多属性效用模型相比，BP神经网络模型的稽查正确率从33%提升至67%，而且省去了复杂的权重确定过程，另外有效的学习能力使其具有较好的适应性，对提升高速公路稽查水平具有很大帮助。

5 结语

本文提出了以车辆信用度作为衡量逃费可疑度的量化指标，给出了基于BP神经网络模型的车辆信用度计算方法。该研究成果已实际应用于浙江省某高速公路公司，取得了较好的效果。稽查部门根据模型给出的信用度值，实现了对逃费可疑车辆的精准稽查，降低了工作强度。不过，本文提出的模型对于没有在收费系统中留下逃费痕迹的逃费行为不具备稽查能力，在下一步研究中，将提升算法的自学习能力，降低算法对样本的依赖程度，例如可考虑深度学习等算法；采用模糊数学模型实现对车辆信用度的评价，有效降低对异常行为次数值的依赖，使模型的准确率更高。

参考文献

[1]张友权.浅谈高速公路车辆逃费的主要方式及其应对策略[J].北方交通，2011（8）：66-68.

[2]杨伟明.高速公路联网收费逃费作弊情况分析及其对策[J].中国高新技术企业，2007（15）：144-147.

[3]杨淑芹.联网收费防止利用通行卡逃漏费的途径和有效措施[J].交通世界（运输·车辆），2005（11）：51-53.

[4]潘亮华.高速公路逃费手段及防治办法[J].中国交通信息化，2011（2）：99-100.

[5]韩慧英.高速公路逃费探源[J].安全与健康，2005（22）：10.

[6]唐州生.高速公路车辆偷逃通行费的原因及应对措施[J].西部交通科技，2011（3）：70-73.

[7]DELBOSC A,CURRIE G.Cluster Analysis of Fare Evasion Behaviours in Melbourne,Australia[J].Transport Policy,2016,50:29-36.

[8]GUARDA P,GALILEA P,PAGET-SEEKINGS L,et al.What is Behind Fare Evasion in Urban Bus Systems?An Econometric Approach[J].Transportation Research Part A:Policy&Practice,2016,84:55-71.

[9]TRONCOSO R,GRANGEE L D.Fare Evasion in Public Transport A:Time Series Approach[J].Transportation Re⁃search Part A:Policy&Practice,2017,100:311-318.

[10]JANKOWSKI W B.Fare Evasion and Noncompliance:A Game Theoretical Approach[J].International Journal of Transport Economics,1991,18(3):275-287.

[11]刁洪祥.ETC系统客户数据异常检测方法的研究[D].长沙：长沙理工大学，2004.

[12]刁洪祥.基于模糊C-均值聚类的ETC系统客户的逃费分析研究[J].企业技术开发，2005（10）：8-10.

[13]刁洪祥.基于稳定遗传神经网络的ETC系统客户逃费分析[J].电脑与信息技术，2006（4）：16-19.

[14]刁洪祥，刘伟铭.基于BP神经网络的ETC系统客户的流失分析研究[J].企业技术开发，2006（9）：34-36.

[15]刘勇，刁洪祥，刘伟铭.基于改进的模糊决策树ETC系统客户欺诈分析研究[J].交通与计算机，2006（2）：1-4.

[16]赵彦，吴淑玲，林志恒，等.高速公路通行卡逃费行为预测模型研究[J].中国科技论文，2015,10（19）：2245-2251.

[17]张晓航.高速公路联网收费稽查管理应用研究[D].西安：长安大学,2010.

[18]王小川.MATLAB神经网络43个案例分析[M].北京：北京航空航天大学出版社，2013.