新能源小汽车的发展对交通拥堵的影响

张 彭，雷方舒，朱 珊，朱广宇

（1.交通运输部规划研究院，北京 100028；2.北京交通发展研究院，北京 100073；3.北京交通大学 城市交通复杂系统理论与技术教育部重点实验室，北京 100044）

0 引言

新能源汽车是能源安全和环境保护要求下汽车工业发展的必然趋势，但较低的能源成本刺激了车辆使用，增加了道路交通压力。随着新能源小汽车在机动车保有量中占比的增加，其对拥堵的影响逐渐凸显。为了兼顾节能减排与缓解拥堵，科学制定城市交通可持续发展战略，需要分析并预测新能源小汽车的发展对交通拥堵的影响。

目前该问题处于粗略的定性分析阶段：孙正良等[1]指出，新能源汽车的爆发性增长会引起交通流增速的加快；龚露阳[2]提出发展新能源汽车要制定效果和影响评价指标体系。而该问题的定量分析尚属空白，需要通过建模仿真才能完成，目前可利用的主流仿真模型包括三类：基于四阶段法的模型（Four-Stage Model）、元胞传输模型（Cell Transmis⁃sion Model，简称CTM）和宏观基本图（Macroscop⁃ic Fundamental Diagram，简称MFD）。根据对需求的定义、需求的产生、划分的方法不同，四阶段法模型又可分为三个子类：经典模型[3-4]、基于出行链的模型[5-6]和基于活动的模型[7]。根据需求变化与路网运行之间的交互关系，又存在静态模型与动态模型之分[8-9]。该类方法需要对每条路段建模，在应用过程中，由于受道路拓扑、信号灯周期、机非混行、路侧停车等各种因素影响，路段特性千差万别，建立广泛适用的路段模型并标定参数十分困难。对于这一研究而言，需要根据新能源小汽车的增量和出行特征计算增加的OD交通量，并将其分配到路网进行仿真，其建模复杂度高、仿真效率低。

CTM由Daganzo等[10]研究提出，用以分析交通走廊中不同区块的空时影响关系。之后，Sumalee等[11]提出了随机元胞传输模型（Stochastic Cell Transmission Model，简称SCTM），用以描述供需不确定条件下的宏观交通流动态特性。Szeto等[12]提出了增强的CTM方法（Enhanced Lagged CTM）。这类方法多用于对交通走廊的仿真，在大规模路网仿真中应用较少。

由Geroliminis等[13]研究提出的MFD，被用以描述区域内在网车辆数与网络运行水平之间的关系[14]，在网车辆数与区域输出流量的关系，区域内总流量与车辆密度之间的关系[15]，以及总行驶里程与总行驶时间之间的关系[16]。在此基础上，Knoop等[17]提出了广义宏观基本图（Generalized Macroscop⁃ic Fundamental Diagram，简称GMFD）；Keyvan-ek⁃batani等[18]将MFD应用于分析区域外围卡口交通控制对交通运行的影响；Yildirimoglu等[19]将MFD的框架与动态分配结合起来。MFD从宏观上建立了交通要素之间的联系，仿真效率较高，但未揭示拥堵形成及消散过程中各宏观要素之间相互影响的动态关系。由于难以区分新能源车和燃油车的出行特征，该方法对研究目标不适用。

此外，张彭等[20]提出了需求管理（Travel De⁃mand Management，简称TDM）对路网运行影响的系统级仿真方法。该方法将路网视为一个动态系统，使用大数据抽象出若干系统级要素，通过建立各要素间相互制约、相互影响的理论关系，对路网运行动态过程进行描述，进而将问题转换为近代控制论中的经典问题，用状态空间分析的方法进行求解。使用该模型可实现对多种TDM政策实施效果的仿真，同时由于使用有限的浮动车数据即可对模型进行标定，该方法建模速度快、仿真效率高。

新能源小汽车对路网运行的影响本质上是一种特殊的出行需求加载于路网的结果。因此，本研究首先推算新能源小汽车的需求特征，然后将需求特征与预计增加的保有量相乘，并代入系统级路网模型，计算出需求增加对路网运行速度的影响。该方法不需要建立由路段组成的路网模型，从而极大地降低了建模复杂度，提高了仿真效率，同时可以给出新能源小汽车对全天不同时段交通运行的影响差异。

1 出行需求联合分布模型

设出行需求的联合分布为P(u,t)，其中：t为出发时间；u为车辆以自由流速度完成OD所需时间，又称为出行的自然需求，通过计算行程经由路段的自由流行驶时间之和获得。每条路段的自由流行驶时间为路段长度除以路段自由流速度。以间隔时间Δt对t离散化，则P(u,t)转化为P(u,i)。图1（a）和图1（b）分别为燃油车和新能源小汽车单日的出行需求联合分布(u,i)，其描述了两类车辆不同的出行需求特征。

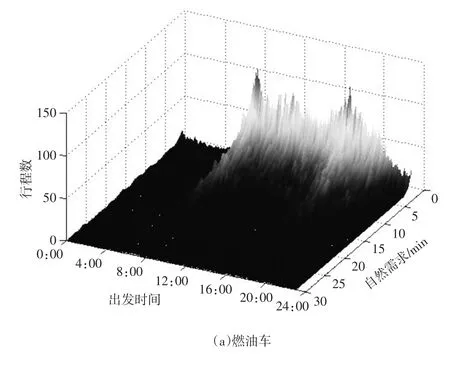
图1 出行需求联合分布

2 系统级路网仿真模型

模型将路网运行视为一个具有独立输入和输出的系统，其中输入为出行需求的联合分布(u,i)，输出为路网平均速度v(i)，系统具有若干内部状态变量。首先建立描述各变量之间的动态关系的方程组，然后将其转换为系统的控制模型。

2.1 需求与路网运行之间的关系

周期性计算路网负荷r和路网均速v可得到二者的对应关系。其中，路网负荷为同时在途车辆数。图2为基于2015年5月30日的数据获得的对应关系散点图，计算周期为5min。

图2 路网负荷与路网均速关系图

对散点进行拟合可得r与v的关系（图2中的曲线），设其函数为：

图3描述了需求变化与路网运行的交互关系，其中虚线代表不同时刻进入路网车辆需求的联合分布(u,i)，点划线代表时刻i之前上路的车辆在时刻i尚未完成的自然需求，称为剩余需求。时刻i新上路车辆的自然需求和时刻i之前上路车辆的剩余需求共同构成了时刻i的总需求，其分布如图3中实线所示。

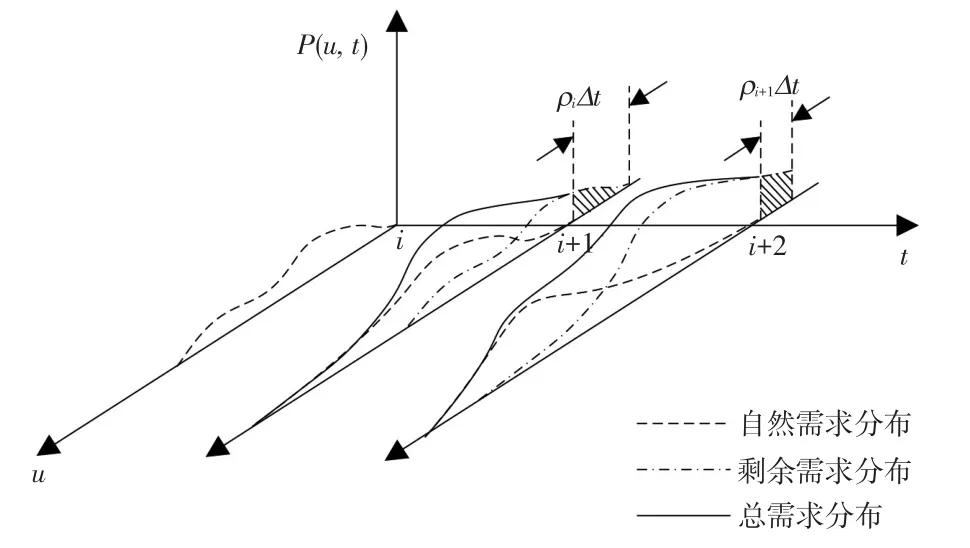
图3 需求变化与路网运行的关系

计算时刻i的路网负荷，将其代入式（1）可得对应的路网速度v(i)：

在Δt内车辆实际完成的自然需求与以自由流行驶所能完成的自然需求之比为，令其为ρi，其中vf为自由流速度，即：

Δt内平均每辆车完成的自然需求为ρiΔt，未完成部分作为剩余需求转移至i+1时刻，相当于将(u,i)沿u轴负方向整体平移ρiΔt，如图2中i+1时刻点划线所示。平移后的(u,i)中u≤0部分代表驶离路网的车辆，u＞0部分代表未能驶离路网的车辆，令其为(u,i)，如式（4）所示：

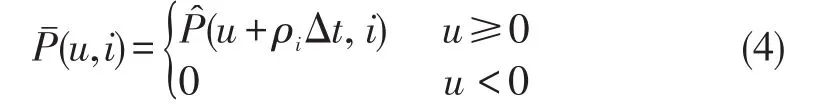
(u,i)与i+1时刻新上路车辆的自然需求分布(u,i+1)共同构成了i+1时刻的总需求，其分布为P(u,i+1)，如图2中i+1时刻实线所示，用公式可表示为：

对应的路网负荷r(i+1)为：

将r(i+1)代入式（1）可得出i+1时刻的路网速度v(i+1)，根据式（4）可得对应的剩余需求分布(u,i+1)。如此迭代即可获得路网负荷与路网速度之间相互作用、迭代演进的过程。

2.2 TDM的系统级模型

式（2）～式（6）可以转换为需求方程（7），用以描述路网负荷的构成：

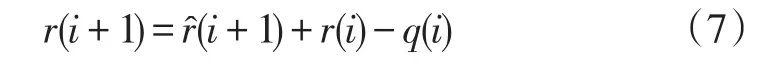
式（7）中：r(i+1)为i+1时刻的路网负荷；为i+1时刻新上路的车辆数；为之前上路截至i时刻仍在途的车辆数；为i时刻驶离路网的车辆数。

将式（2）及式（3）代入q(i)可得供给方程（8），其描述了当前路网运行状态对路网负荷的减少程度：

图4为TDM系统框图。式（2）～式（6）构成路网系统A，(u,i)和v(i)分别为系统输入和输出，z-1为对出发时间i时移的z域表示，filter(u)为对出行需求分布的时移，B为TDM策略。

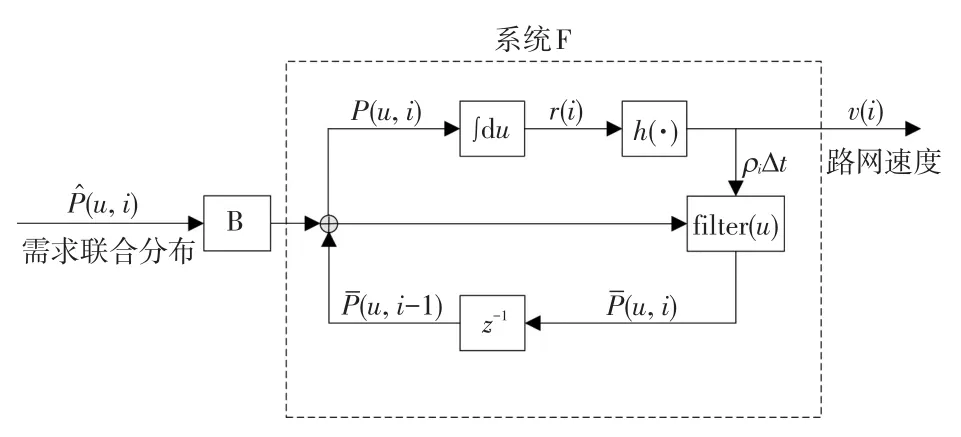
图4 TDM系统级仿真框图

如此即可根据出行需求联合分布(u,i)获得路网速度v(i)。模型的有效性验证见文献[20]。

3 新能源小汽车的发展对交通拥堵的影响分析

3.1 仿真方法

需求包括需求特征和需求规模两方面。新能源小汽车对交通拥堵的影响由其需求特征和发展规模共同决定，以各自规模为权值，将燃油车和新能源车的需求特征加权求和可得到路网的总需求：

其中，规模等于保有量乘以出车率。将总需求作为输入代入图（4）给出的系统模型可获得路网速度的变化过程。新能源车和燃油车的需求特征根据历史数据标定，在一段时期内相对固定，通过调节权值大小可仿真不同发展规模对路网运行的影响，也可根据设定的路网速度推算对应的发展规模。

3.2 数据源

本研究数据来自装有信息采集设备的社会车辆，其中新能源车为电动小汽车。通过无线传输设备实时采集车辆GPS位置、油耗、充放电、点火时间、熄火时间等数据。数据空间范围：北京市中心城1 368km2，路段数40 419。时间范围：燃油车2017年3月6日至2017年3月10日，新能源车2016年7月18日至22日。样本车辆数：燃油车12 000辆，新能源车4 700辆。假设样本燃油车和样本新能源车分别均匀混合于全部燃油车和全部新能源车，则可分别作为对同类社会车辆的采样。GPS采集间隔30s，与地图匹配后可得车辆行驶轨迹，路径匹配正确率大于95.6%。行程的起止切分规则为连续5min GPS位置的标准差小于20m。仿真计算采用SQL Server结合Matlab的方式进行。

3.3 仿真结果

在现有小汽车保有量的基础上，分别单独增加10万、30万、50万的新能源车和燃油车，仿真路网均速在高峰时段和全天的变化。其中，早高峰为07:00—09:00，晚高峰为17:00—19:00，全天是指06:00—22:00。数据采集时间为2017年3月6日至3月10日，连续5个工作日。对出车率和样本比例均做归一化处理，逐天仿真并求均值，结果见表1。

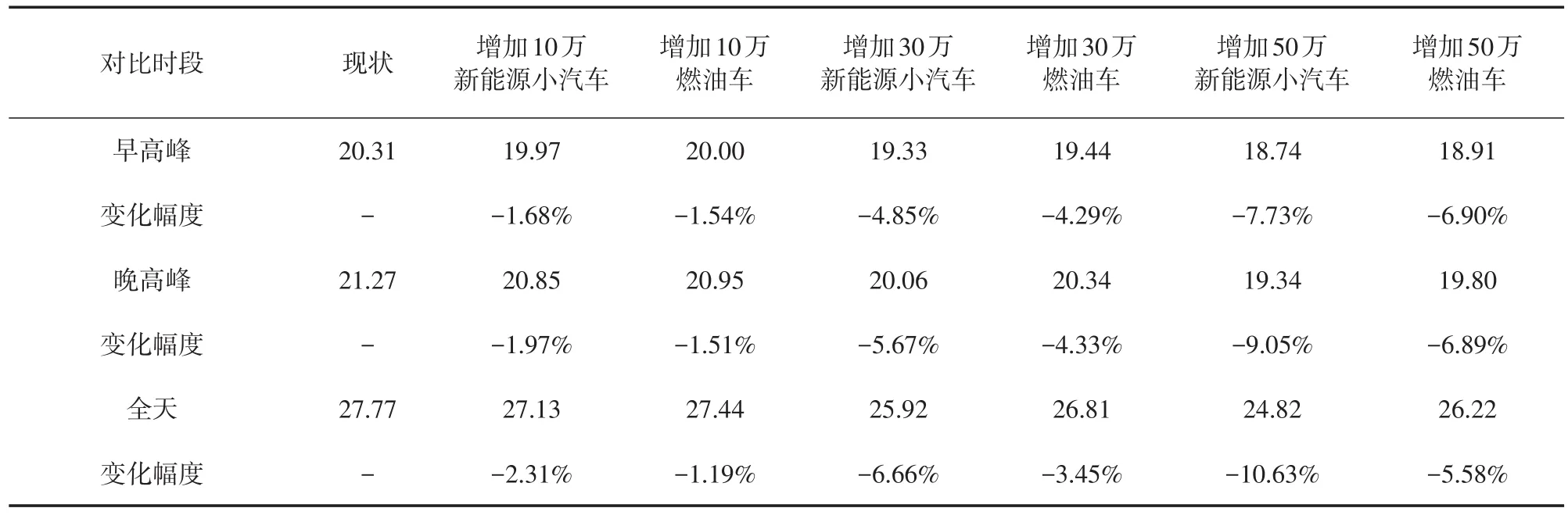
表1 新能源小汽车与燃油车保有量增加对路网均速影响对比（单位：km/h）

从表1可以看出，同样增量的新能源小汽车对交通拥堵的影响显著大于燃油车，对全天的影响大于对高峰时段的影响，对晚高峰的影响大于对早高峰的影响。

北京市按尾号将小汽车分为五组实行轮流限行，不同尾号组合占比见表2。由于尾号为4的车辆仅占1.7%，尾号为4、9的组合占总数的13.9%，较其他4种组合的均值（21.5%）明显偏小，导致4、9限行日被限车辆少、出行车辆多，交通拥堵较严重。

表2 不同尾号组合占比

尾号4、9限行日相对于非4、9限行日的高峰及全天路网均速降幅分别为5.2%及5.8%。以2016年底为基准，使用模型推算未来小汽车保有量增加多少后，非4、9限行工作日的路网均速将等同于基准4、9限行日，结果如表3所示。

表3 现4、9限行拥堵状态对应的未来机动车保有增加量

根据表3可知，在人口规模、出行结构等外部条件不变的前提下，分别单独发展燃油车43.7万或新能源车30.4万时，非4、9限行日的高峰拥堵程度将相当于基准时期的4、9限行日，新能源小汽车将以较小的增量达到燃油车的增堵效果。

2016年北京市摇号政策设定每年9万辆燃油车和6万辆新能源车的保有量增速。本研究设定了另外三种年保有量增速的假设方案，与现政策方案进行对比。假设方案见表4。

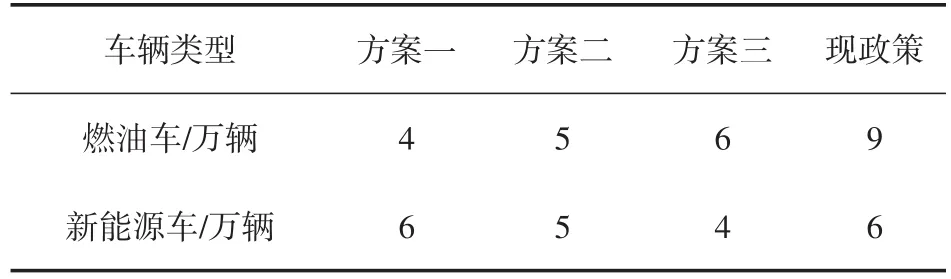
表4 现行限号方案与假设方案

对需求增加后，不同方案下，未来非4、9限行日路网均速降低至目前4、9限行日所需年限进行仿真，仿真结果如表5所示。

从表5可看出，三种假设方案实施3～4年后，非4、9限行日的高峰拥堵状态将等同于目前4、9限行日，较现行方案延缓拥堵约1年。机动车保有量的持续增加以及高强度使用是导致交通拥堵的主要原因，不同方案的缓堵效果也都有限。

4 结论

借助于系统级路网模型，本文仿真了新能源小汽车的发展对交通拥堵的影响，结果显示：较低的能源成本刺激了新能源车的使用强度，导致其对交通拥堵的影响显著大于燃油车。由于文中结果仅根据一周数据仿真获得，而天气、季节、城市规模等因素变化均会影响模型参数取值，长期性影响还需采用Monte Carlo法，用历史数据逐天标定模型参数，对结果进行回归获得。此外，文中数据仅来自于纯电动车，关于混合动力等其他类型新能源车对拥堵的影响有待进一步研究。

参考文献

[1]孙正良，江帆，虞立英.新能源汽车发展对城市交通管理的影响[J].交通信息与安全,2016，34（6）：108-113.

[2]龚露阳.新能源汽车在交通运输行业推广应用策略研究[J].综合运输，2017，39（2）：35-42.

[3]KIM I,HWANG K Y,EOM J K.Building a TDM Impact Analysis System for the Introduction of Short-Term Conges⁃tion Management Program in Seoul[J].Journal of Korean So⁃ciety of Transportation,1999,17(1):173-185.

[4]KIM I,HWANG K Y,CHO Y H.Application of Sub-Area Analysis Techniques for TDM Policy Analysis[J].Journal of the Korean Society of Civil Engineers,2000,20(6D):635-635.

[5]JONNALAGADDA N,FREEDMAN J,DAVIDSON W,et al.Development of Microsimulation Activity-Based Model for San Francisco:Destination and Mode Choice Models[J].Transportation Research Record,2001,1777(1):25-35.

[6]AXHAUSEN K W,GÄRLING T.Activity-Based Approach⁃es to Travel Analysis[J].Transport Reviews,1992,12(4):323-341.

[7]BOWMAN J L,BEN-AKIVA M E.Activity-Based Disag⁃gregate Travel Demand Model System with Activity Sched⁃ules[J].Transportation Research(Part A:Policy and Prac⁃tice),2001,35(1):1-28.

[8]BEN-AKIVA M E,GAO S,WEI Z,et al.A Dynamic Traf⁃fic Assignment Model for Highly Congested Urban Networks[J].Transportation Research(Part C:Emerging Technolo⁃gies),2012,24(24):62-82.

[9]CAREY M,WATLING D.Dynamic Traffic Assignment Ap⁃proximating the Kinematic Wave Model:System Optimum,Marginal Costs,Externalities and Tolls[J].Transportation Research(Part B:Methodological),2012,46(5):634-648.

[10]DAGANZO C F.The Cell Transmission Model,PartⅡ:Net⁃work Traffic[J].Transportation Research(Part B:Methodolog⁃ical),1995,29(2):79-93.

[11]SUMALEE A,ZHONG R X,PAN T L,et al.Stochastic Cell Transmission Model(SCTM):A Stochastic Dynamic Traffic Model for Traffic State Surveillance and Assignment[J].Transportation Research(Part B:Methodological),2011,45(3):507-533.

[12]SZETO W Y.Enhanced Lagged Cell-Transmission Model for Dynamic Traffic Assignment[J].Transportation Re⁃search Record,2009,2085(2085):76-85.

[13]GEROLIMINIS N,DAGANZO C F.Existence of Urban-Scale Macroscopic Fundamental Diagrams:Some Experi⁃mental Findings[J].Transportation Research(Part B:Meth⁃odological),2008,42(9):759-770.

[14]DAGANZO C F.Urban Gridlock:Macroscopic Modeling and Mitigation Approaches[J].Transportation Research(Part B:Methodological),2007,41(1):49-62.

[15]GEROLIMINIS N,SUN J.Properties of a Well-Defined Macroscopic Fundamental Diagram for Urban Traffic[J].Transportation Research(Part B:methodological),2011,45(3):605-617.

[16]CASSIDY M J,JANG K,DAGANZO C F,et al.Macroscop⁃ic Fundamental Diagrams for Freeway Networks:Theory and Observation[J].Transportation Research Record,2011,2260(2260):8-15.

[17]KNOOP V L,LINT H V,HOOGENDOORN S P.Traffic Dy⁃namics:Its Impact on the Macroscopic Fundamental Dia⁃gram[J].Physica A:Statistical Mechanics and Its Applica⁃tions,2015,438(438):236-250.

[18]KEYVAN-EKBATANI M,KOUVELAS A,PAPAMICHAIL I,et al.Exploiting the Fundamental Diagram of Urban Net⁃works For Feedback-Based Gating[J].Transportation Re⁃search(Part B:Methodological),2012,46(10):1393-1403.

[19]YILDIRIMOGLU M,RAMEZANI M,Geroliminis N.Equi⁃librium Analysis and Route Guidance in Large-Scale Net⁃works with MFD Dynamics[J].Transportation Research(Part C:Emerging Technologies),2015,59:404-420.

[20]张彭，雷方舒，张晓松，等.机动车出行需求管理对路网运行影响的系统分析方法[J].交通运输系统工程与信息，2017，17（1）：227-234.