建立表层嵌贴FRP板条-混凝土界面黏结-滑移模型的方法

张智梅,张振凯,熊 浩,王 卓,陈 刚

表层嵌贴纤维增强复合材料(fiber reinforced polymer,FRP)加固混凝土结构技术相较于外贴FRP加固技术,在改善黏结性能、提高FRP利用率、减少恶劣环境对FRP的影响等方面都表现出明显优势[1-2],因而越来越广泛地被用于加固工程实践中.目前,用于表层嵌贴加固的FRP主要有FRP板条和各种截面形式的FRP筋,其中FRP板条截面具有更大的周长面积比,其界面黏结性能更优于FRP筋材.

尽管如此,已有的有关表层嵌贴FRP板条加固混凝土构件的研究结果表明,界面剥离破坏仍是造成加固构件失效的主要因素[3-8].为此,学者们围绕表层嵌贴FRP板条-混凝土界面破坏机理开展了一系列试验研究[9-14].但因其界面的受力较外贴FRP板条-混凝土界面更为复杂,影响因素更多,加之试验方法的不同,使得现有的试验数据不仅有限而且离散性大.试验数据的离散,使得利用传统的通过测量在黏结长度范围内沿FRP板条各测量点的应变来建立局部黏结-滑移关系的方法变得不可靠.不过无论采用何种试验方法,黏结节点在加载端、自由端的滑移值和加载端施加的荷载值一般都可准确获取.

基于此,本研究提出了一种数值分析方法.通过该方法,可以只利用上述可靠的试验数据来标定黏结-滑移模型中的未知参数,从而准确建立界面黏结-滑移本构方程.在此基础上,进一步探讨了表层嵌贴FRP板条加固混凝土梁的裂缝宽度和间距的计算方法.

1 局部黏结-滑移控制微分方程的建立

本研究的分析主要采用以下假设:①FRP为线弹性材料;②FRP板条横截面上正应力均匀分布;③同一截面的界面剪应力沿FRP板条宽度和厚度均匀分布;④忽略混凝土的位移,即FRP板条的位移值即为其相对于混凝土的滑移值.

1.1 FRP板条-混凝土界面黏结-滑移控制微分方程的建立

取受到轴向拉力作用的,嵌贴在混凝土中的FRP板条微段d x.为了更符合实际,本研究考虑FRP板条在两侧面及顶面均与混凝土可靠黏结,受力分析如图1所示,其中x轴原点取为板条的自由端,τ(x)为FRP板条-混凝土界面的黏结剪应力,tf,wf分别为FRP板条截面的厚度和宽度.根据上述假设,由x方向力的平衡方程,以及FRP板条应变与滑移值s的关系,可建立FRP板条滑移控制微分方程为

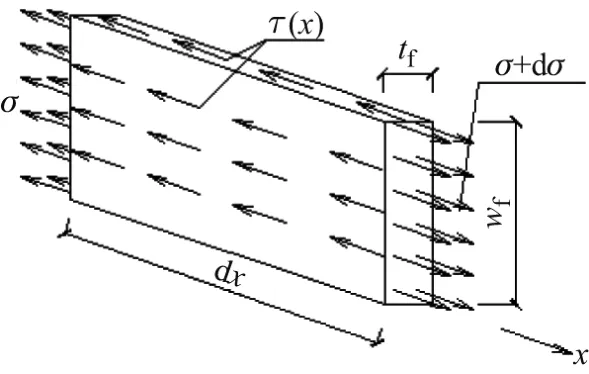
图1 FRP板条微段受力分析Fig.1 Stress analysis of the FRP strips

式中:Ef为FRP的弹性模量;s为FRP板条滑移值,由假设①,s的相对值与绝对值相等;其实质为表征FRP板条几何特征和物理特性的常数.由式(1)可知,若τ(s)为已知,则在一定的边界条件下求解该微分方程,即可求得相应的板条滑移值s(x)及其一阶导数s′(x).由此可进一步得到FRP板条任意截面上的轴力为

式中,Af为FRP板条截面面积.由上述分析可知,选取的τ(s)与实际界面性能越接近,通过解微分方程得到的FRP板条滑移理论值与试验值相差也就越小.因此,选取合理的τ(s)对方程求解至关重要.

1.2 界面局部黏结-滑移模型τ(s)的选取

本研究在分析对比了若干典型的表层嵌贴FRP板条-混凝土界面τ(s)模型后,选取了如图2所示的τ(s)模型进行数值方法的分析.

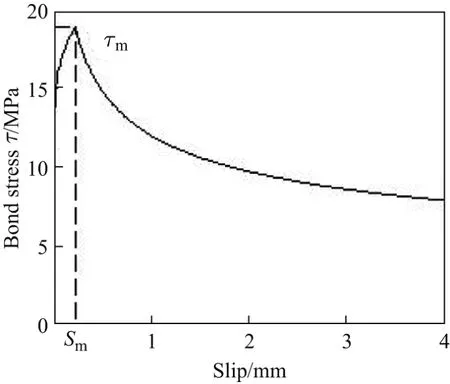
图2 局部黏结-滑移模型Fig.2 Local bond-slip model

上升段(见式(3))与典型的BEP(Bertero-Eligehausen-Popov)模型上升段相同[15],下降段(见式(4))则取自De-Lorenzis等[16]的研究.

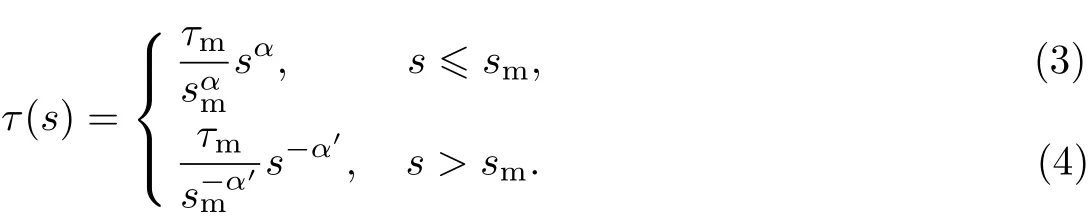
将式(3),(4)代入式(1)中,可得微分控制方程的具体形式为

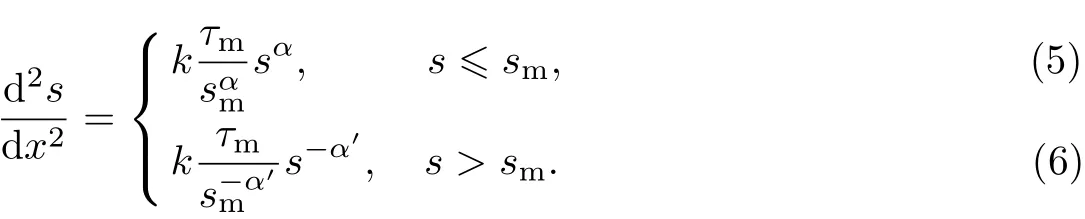
该模型不仅物理意义明确,形式简单,而且便于微分方程的求解,其中参数τm和sm分别表征界面的黏结强度及其相应的滑移值,参数α和α′为控制黏结-滑移曲线形状的两个参数.通过本研究提出的方法,利用该模型得出的理论分析结果能与试验数据较好地吻合.

2 微分方程的求解与局部黏结-滑移模型中待定参数的标定

2.1 控制微分方程的求解及误差计算

在黏结试验中,通常可准确获取FRP板条在各级荷载Ni(i=1,2,···,n)作用下的加载端滑移值sli和自由端滑移值sfi. 在给定 τ(s)模型中所包含的参数 p(τm,sm,α,α′)的值后,根据边界条件sfi或sli求解微分方程(5),(6),即可求得与荷载试验值Ni相对应的理论值N(sfi)或N(sli).此时,荷载理论值与试验值之间的误差Δp,可反映出由给定参数p所确定的界面黏结-滑移模型τ(s)与黏结界面实际情况吻合的程度.据此,对参数p的取值进行优化,直到理论值与试验值间的误差满足规定的误差限值.为便于描述,设FRP板条在自由端处的坐标为x=0,滑移为sf;在加载端处的坐标为x=l,其中l为FRP板条的黏结长度,滑移为sl.

2.1.1 确定自由端滑移sf=0时,加载端荷载最大值N0,m对应的滑移值sl0,m

先在边界条件s(0)=0,s′(0)=0下求解方程式(5),得到滑移及其一阶导数的解析解:

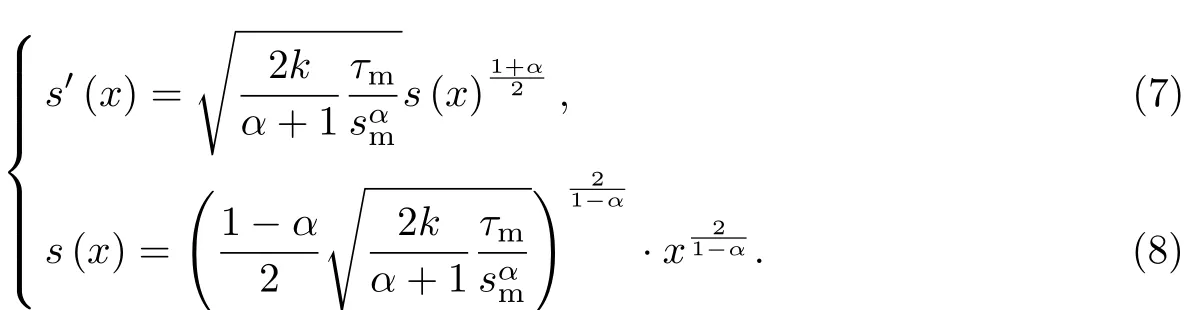
将x=l代入式(8),可得加载端的滑移sl.若sl≤sm,则

把sl=sm代入式(9),可得当sf=0且sl=sm(即s(x)≤sm)时,FRP的锚固长度为

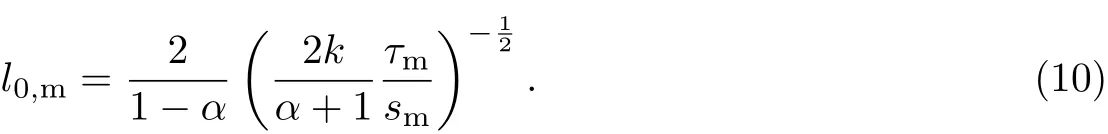
根据黏结长度l是否大于l0,m,可分别解得sl0,m的数值解和解析解,求解过程如图3所示.

2.1.2 根据FRP板条自由端滑移试验值sfi确定加载端荷载的理论值N(sfi)

(1)当sfi=0时,分析可知sfi与加载端(即x=l处)荷载的理论值N(sfi)并非一一对应.为编程方便,可取N(sfi)=Ni.

(2)当sfi＞0时,可在边界条件s(0)=sfi,s′(0)=0,x ∈ [0,l]下求解微分方程(5),(6),得到滑移s(x)和s′(x)的数值解,进而根据式(2)求得加载端(即x=l处)荷载的理论值N(sfi).求解过程如图3所示.

2.1.3 根据FRP板条加载端滑移试验值sli确定加载端荷载的理论值N(sli)

(1)当sli≤sl0,m时,由2.1.1节可知,FRP板条在自由端附近一定范围的滑移均为0,此时:①若sli≤sm,可直接将s(x)=sli代入式(7)得到相应的s′li,进而求得N(■);②若sli＞sm,可知在黏结长度范围必有某点x=xmi,满足s(xmi)=sm,s′(xmi)=加之s(l)=sli,以此为边界条件,在s∈[sm,sl]范围对式(6)积分可得

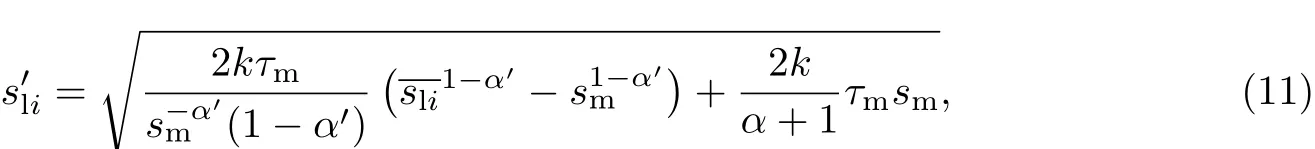
进而可求得N(sli).

(2)当sli＞sl0,m时,FRP板条自由端已产生滑移,可在边界s(l)=sli,s′(0)=0,x ∈[0,l]下解微分方程式(5),(6),求得滑移s(x)和s′(x)的数值解,进而根据式(2)求得加载端荷载的理论值N(sli).求解过程如图3所示.

2.1.4 荷载试验值与理论值之间的误差分析

本研究采用下式来分析荷载试验值与理论值之间的误差:

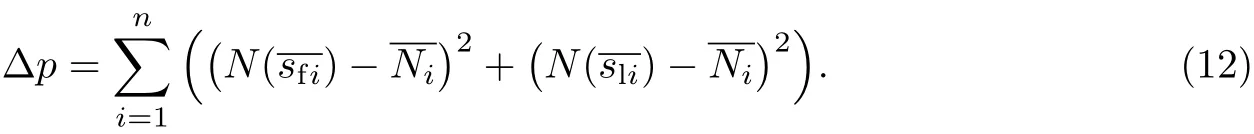
为实现上述数值分析过程,利用MATLAB进行编程(见图3).

2.2 参数组 p(τm,s m,α,α′) 取值的优化

为使荷载理论值与试验值的误差足够小,即保证由参数值p(τm,sm,α,α′)确定的τ(s)关系与实际的界面黏结-滑移性质足够吻合,需对p(τm,sm,α,α′)的取值进行优化.由于涉及多个变量,本研究采用非线性优化中的Nelder-Mead算法[17]对参数p进行优化.该算法无需任何求导运算.根据该算法,重复执行流程图3,每循环一次都使误差Δp逐步缩小.当误差小于规定限值时,则认为由优化后的p(τm,sm,α,α′)值所确定的τ(s)关系为界面黏结-滑移模型.

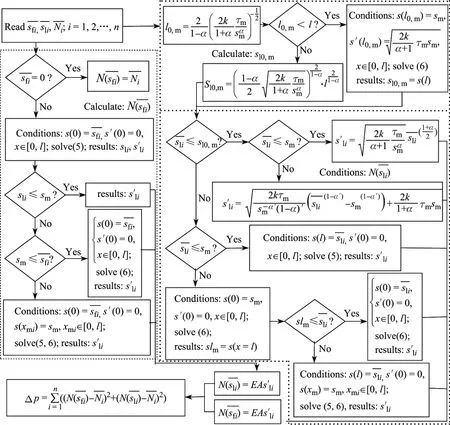
图3 数值分析流程图Fig.3 Flowchart diagram of numerical analysis

2.3 实例验证

为验证上述数值方法的有效性,本研究选取了文献[18]中表层嵌贴FRP板条黏结节点试件在单调加载下的试验数据.数据共9组,每组3个相同试件,共计27个试件.混凝土强度分别为C35,C45和C70,锚固长度分别为40,60,80 mm.FRP弹性模量Ef=160 000 MPa,厚度tf=1.39 mm和宽度wf=9.34 mm保持不变.对所有试件均按2.2节方法确定了τ(s)关系中的系数p(τm,sm,α,α′),计算结果如表1所示.受篇幅所限,图4仅给出了混凝土强度为70 MPa,黏结长度分别为40,60,80 mm的各试件的N-sf和N-sl的理论值与试验值的对比.可以看出,各组数据的试验值和理论值均非常吻合.对文献[18]中其他试件进行同样的分析也得到了很好的结果.这说明利用本研究提出的数值分析方法可以准确确定界面黏结性能.

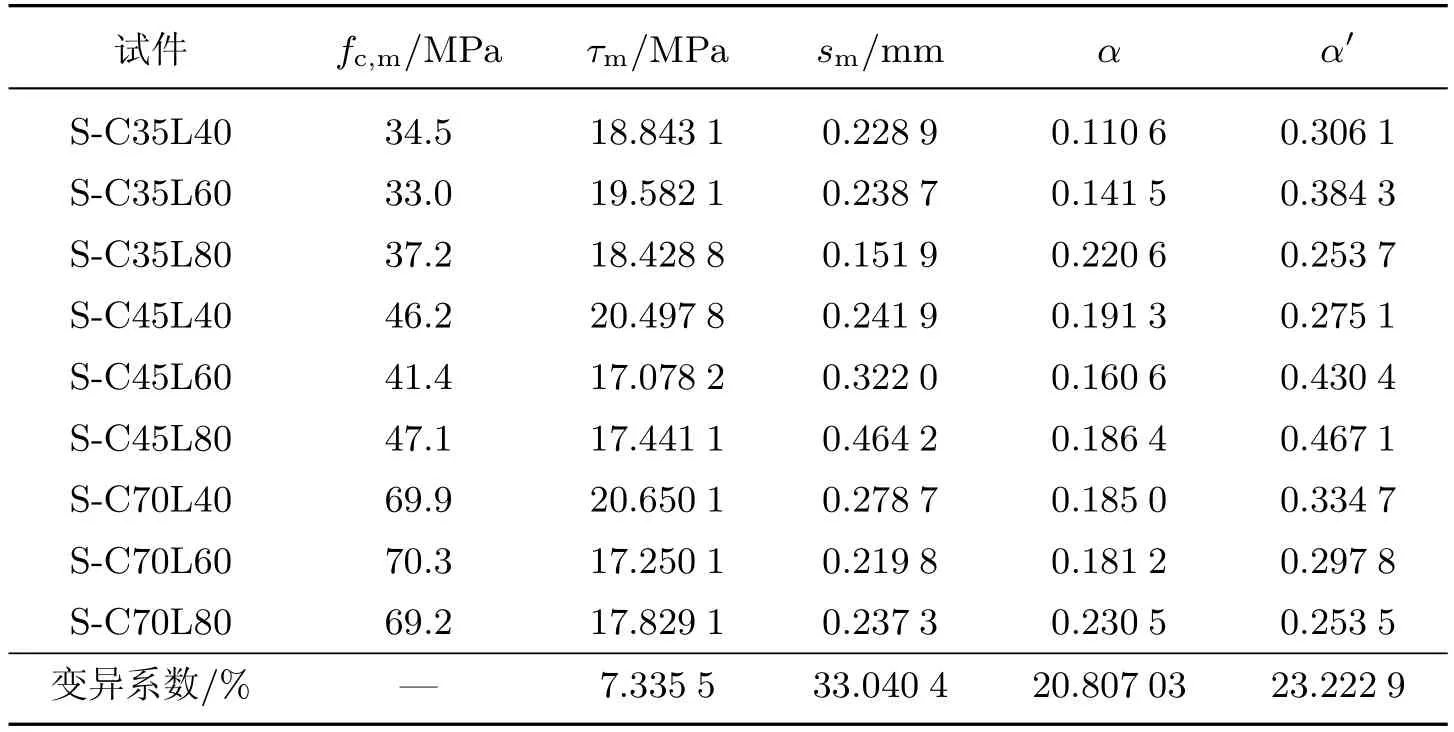
表 1 参数组 p(τm,s m,α,α′)的优化结果Table 1 Optimization results of p(τm,s m,α,α′)

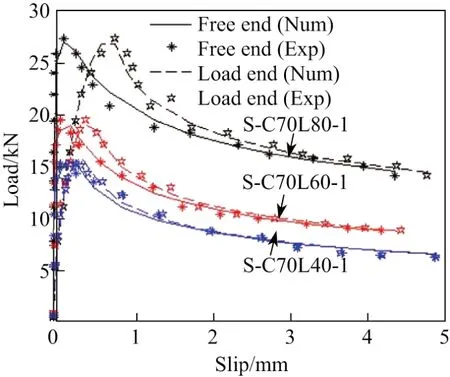
图4 N-s理论值与试验值的对比Fig.4 Companisons of the numerical and experimental results of the relationship N-s

3 参数p的优化结果及影响因素分析

3.1 优化结果

依据文献[18]中27个试件单调加载试验获得的Ni及相应的sli和sfi试验值,根据图3中的求解流程对全部试件进行分析,结果如表1所示.从表1中各参数的变异系数可以看出,黏结强度τm的变异系数较合理,而其余3个参数的变异性较大,说明若取其平均值来作为表层嵌贴FRP板条-混凝土界面黏结-滑移模型中的参数将引起较大误差.因此,需进一步探讨各参数与影响界面性能的主要因素之间的关系.

3.2 影响因素分析

根据表1,本研究首先分析了黏结长度l对黏结强度τm的影响,通过拟合分析得τm=36.556 l−0.1667,如图5(a)所示.进一步地,将τm/l−0.1667与混凝土强度fc,m进行拟合分析,结果如图5(b)所示.可见,混凝土强度fc,m对τm几乎没有影响.

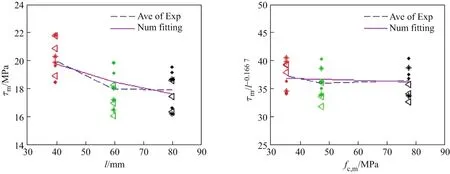
图5 黏结长度和混凝土强度对黏结强度的影响Fig.5 Infl uence of the bond length and strength of concrete on the bond strength

对本构方程中涉及的其他3个参数进行类似处理可知,混凝土强度对这些参数的影响也不大.各参数与黏结长度l的拟合结果为

可以看出,各参数受黏结长度l影响较大,而与混凝土强度的相关性很小.这是因为文献[18]中各试件的破坏主要发生在FRP板条-黏结剂界面,均未发生混凝土表层破坏现象.

4 黏结-滑移关系在混凝土裂缝问题中的应用

4.1 表层嵌贴FRP板条加固混凝土梁的裂缝宽度和裂缝间距的计算

表层嵌贴FRP板条加固混凝土梁在裂缝截面附近的受力分析和截面应变分布如图6所示,其中左侧为已开裂截面a,右侧为临近截面a且即将开裂的截面b.截面b的混凝土受拉区边缘应变正好达到其极限拉应变εtu.由加固梁的裂缝特点可知,ltr较小,且两截面中和轴的变化不明显.为简化计算,假设两截面的中和轴位置相同,又因混凝土即将开裂时仍处于弹性状态,故认为其受压应力-应变关系为线弹性.

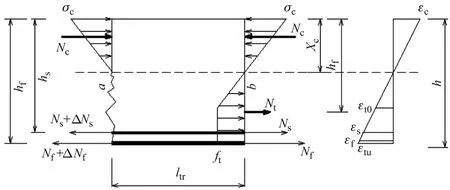
图6 裂缝间混凝土梁的受力分析及截面应变分布Fig.6 Stress model of the members between cracks and strain distribution in cross section of the beam

根据文献[19],混凝土受拉应力-应变关系如图7所示,其中ft为混凝土抗拉强度,εt0为与之对应的弹性拉应变,εtu为混凝土的极限拉应变.根据文献[19]可得

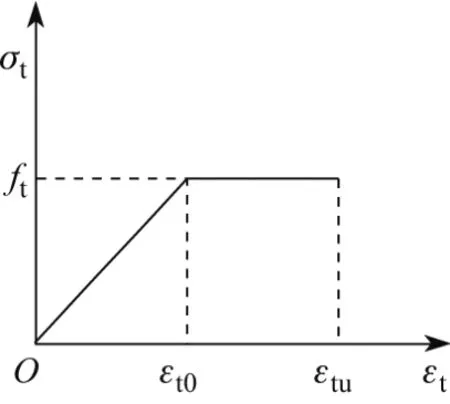
图7 混凝土受拉时的应力-应变关系Fig.7 Stress-strain relationship of the concrete in the tensile region

4.1.1 计算混凝土受压区高度

根据图6可建立截面b在水平方向力的平衡条件.再根据平截面变形假定,引入截面b处混凝土、钢筋、FRP三者应变之间的比例关系,同时考虑式(14),经整理可得

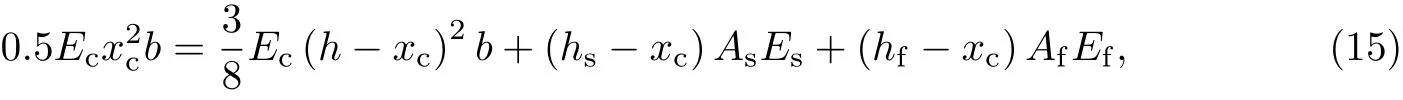
式中,As和Af分别为钢筋和FRP板条的截面面积,Es和Ef分别为钢筋和FRP板条的弹性模量,Ec为混凝土弹性模量,hs和hf分别为钢筋和FRP板条形心到混凝土梁上表面的距离.求解方程(15),即可得到混凝土梁受压区高度xc.

4.1.2 计算裂缝间距ltr所传递的黏结力

由图6混凝土梁段整体力的平衡可知，

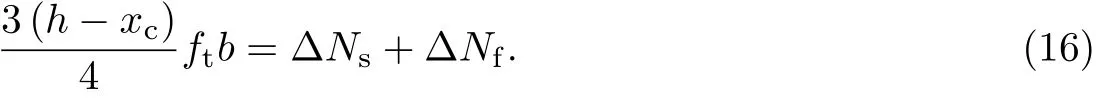
设εs,εf和εs+dεs,εf+dεf分别为截面 b和截面 a 对应的钢筋与混凝土的应变.由平截面假定可知:同时,在截面 a处将其与代入式(16),整理得裂缝间距ltr传递的黏结力为

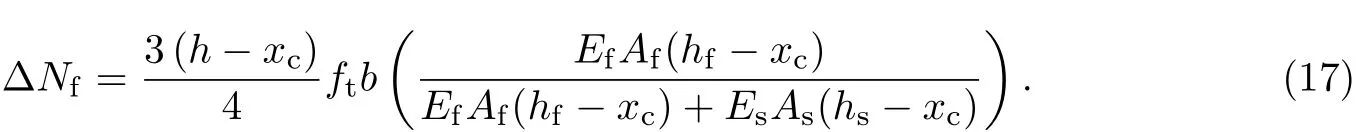
4.1.3 计算最小裂缝长度ltr与裂缝间距str

取截面b处x坐标为0.由于混凝土尚未开裂,故此处FRP板条与混凝土的相对滑移为0,即sf=0,且s′f=0. 由关系式(7),(8)可知,当相对滑移s=sm时,应变此值通常远大于混凝土的开裂极限应变εtu.联合式(2)和式(7),(8),并取N=ΔNf,即可解得最小裂缝间距为

将通过式(17)计算得到的传递荷载ΔNf以及拟合得到的式(13)代入式(18),然后通过迭代法,求得裂缝间距ltr.将x=ltr代入式(8),即可得到裂缝宽度的一半,进而得到裂缝宽度为

4.2 算例分析

为进一步说明利用本研究建立的黏结-滑移模型计算裂缝间距与裂缝宽度的过程,现给出一个计算算例.

梁的截面尺寸为b×h=150 mm×300 mm,开槽尺寸为3.3 mm×15.0 mm;混凝土保护层厚度为as=30 mm,配置2φ6 mm的HRB335螺纹钢,钢筋截面面积为As=56.56 mm2,弹性模量为Es=200 GPa;混凝土极限拉应力为ft=2.787 MPa,弹性模量为Ec=30 GPa;FRP板条宽度为wf=9.34 mm,厚度为tf=1.39 mm,截面面积为Af=12.98 mm2,弹性模量为Ef=160 GPa.

由上述条件可得:hf=300−25/2=287.5 mm,hs=300−30−6/2=267 mm.将相关数据代入式(15)得到混凝土受压区高度x=141 mm.将x代入式(17)得ΔNf=9.02 kN.将ΔNf代入式(18)得最小裂缝间距为ltr=36.8 mm.据此,可由式(13)得到黏结-滑移模型中的参数具体值为τm=20.041 6 MPa,sm=0.243 8 mm,α=0.150 6,α′=0.315 8.将参数值代入式(3),(4),得黏结-滑移具体表达式为τ(s)=24.79s0.1506(s≤sm)或12.83s−0.3158(s＞sm).最后由式(19)计算得到裂缝宽度为str=0.068 mm,此值远小于sm.

5 结论

(1)提出了一种高精度数值分析方法.本方法不受试验方法和试验变量的限制,仅依据黏结节点试验中可靠的FRP板条加载端和自由端的试验数据,即可精确确定所选取的界面黏结-滑移模型中的多个未知参数,从而建立与真实情况相吻合的界面黏结-滑移模型.

(2)利用MATLAB编制程序实现上述数值分析方法.根据具体试验数据准确地确定了黏结-滑移模型中各待定参数,并据此建立了界面黏结-滑移模型.在此基础上进一步分析了混凝土强度和黏结长度等因素对黏结-滑移模型中各参数的影响.

(3)利用本研究建立的黏结-滑移模型探讨了在表层嵌贴FRP加固混凝土梁的裂缝间距和裂缝宽度的计算方法.