椭圆印章自动定位系统的实现

刘志慧

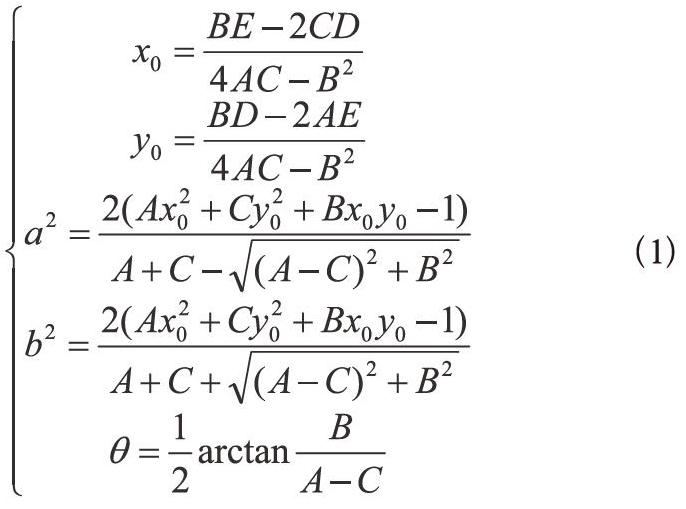
摘 要：自动定位椭圆印章实现的难度在于计算中心、长轴、短轴以及长轴倾角。文中提出一种基于形状特征的椭圆印章自动定位方法，基于集成开发环境Microsoft Visual Studio 2010，应用微软基础类库MFC设计交互界面设计椭圆印章自动定位系统。首先将彩色图像进行预处理，去除彩色图像中的无用信息，然后采用基于曲线弧分割的思想检测椭圆，将轮廓从交点处分割成弧段，随机采样取点求出参数值，准确定位椭圆印章区域。该方法从每一个连续的轮廓弧段中采样，使无效随机采样的概率大大降低。实验结果表明，本系统可以有效定位椭圆印章。

关键词：印章定位；椭圆检测；曲线弧分割；随机采样

中图分类号：TP391.41 文献标识码：A 文章编号：2095-1302（2018）04-00-03

0 引 言

印章具有权威性，被人们应用于各个领域。采用人工多角度对折法可以识别印章真假，然而这种方法需要借助丰富的经验来判别，检测结果具有很强的主观性[1，2]。如何通过计算机快速准确地识别印章已成为需要迫切解决的问题。利用计算机在识别印章真伪操作之前，对操作区域加以限制，以减少无用信息的干扰[3]。因此，自动定位印章作为判断印章真伪的关键步骤，直接关系到判断结果的速度和正确性。如何高效地实现印章的自动定位成为识别印章真伪亟待解决的问题[4，5]。椭圆印章在日常生活中比较常见，鉴于此，本文提出了一种椭圆印章定位方法，并设计了椭圆印章自动定位系统。该系统可在用户干预较少的情况下借助计算机完成椭圆印章的自动定位，为识别印章真伪做好准备。

1 椭圆印章定位算法研究

采集到的测试图像中，印章区域和背景、文字相互重叠，主要包括红色的印章图像和代码编号、灰色或白色的背景、黑色的文字，我们应尽可能多地保留印章图像，去除干扰信息[6，7]，因此需要对原始的印章图像进行预处理。在Windows平台上，基于集成开发环境Microsoft Visual Studio 2010，使用C++语言，并应用微软基础类库MFC设计交互界面[8]，实现椭圆印章自动定位。

1.1 预处理

图像预处理模块主要负责图像中红色分量的提取以及彩色图像的灰度化、二值化，最终得到细化的轮廓图。

首先，将图像的RGB分量值转化到HSI空间中，给这三个分量分别设定合适的阈值。基于 HSI 模型对图像进行初步红色分量提取，将大部分有用信息提取出来，其中红色分量色度余弦值大于0.94，红色的饱和度分量大于20%，红色的亮度分量大于60%[9]。

其次，基于HSI彩色空间模型提取红色分量得到彩色图像，虽然彩色图像包含丰富的图像信息，但占用空间较多，同时也会增大计算量，因此对彩色图像进行灰度化并二值化处理[10]。图像经二值化处理后，目标对象的像素值为1，背景的像素值为0。

最后，基于细化算法由二值图像得到细化的轮廓图[11]。将输入图像中具有一定宽度的线条缩减为宽度是1个像素的线条，在减少信息量的同时保留原图像的拓扑结构。

1.2 椭圆印章定位算法基本思想

本文采用基于曲线弧分割的思想检测椭圆。根据轮廓点间的相互连接性对细化图像中的轮廓像素点进行跟踪。跟踪从起始点开始，将轮廓从交点处分割成弧段，直到所有的轮廓被跟踪完毕。根据各弧段长度的比例，确定在每段弧上采样的次数，在每一个连续的轮廓弧段中采样，求出椭圆参数。椭圆印章定位主要包括曲线弧分割、随机取点求参数以及确定椭圆位置三部分。

1.2.1 曲线弧分割

分配一个与细化图大小相同的二维数组记作array。所有的轮廓跟踪点在array上进行标记，以防止重复跟踪。如果出现极端异常的大轮廓，超出分配内存的大小，则将整个轮廓标记为异常轮廓。对于轮廓过短的情况，也将其标记为异常轮廓。对于异常轮廓不做进一步处理。

曲线弧分割的具体实现步骤如下：

（1）按从下到上、从左到右的顺序扫描轮廓图，将第一个像素灰度值为1的点作为起始点，新建一个坐标链，将此点坐标加入坐标链。

（2） 在array数組中的相应位置进行标记，以防止重复跟踪。

（3）寻找下一相邻点。按右、右上、上、左上、左、左下、下、右下的顺序考察当前点八邻域的8个方向点。如果当前点的八邻域中连通点个数大于2，则说明有其他链路也通过该点，即轮廓出现分支，将当前点作为新的起始点进行轮廓跟踪，转（2）；如果当前点的八邻域中连通点个数大于0且小于等于2，则说明轮廓没有出现分支，将八邻域中像素值第一个为1的点置为当前点，若当前点和起始点重合，则表明已经转了一圈，将当前点在二维数组array的对应位置进行标记，防止重复跟踪，转（4）。若当前点没有与起始点重合，则将此点坐标加入坐标链，链路长度加1，转（2）；如果当前点的八邻域中连通点个数为0，则转（4）。

（4） 轮廓图中若仍存在像素灰度值为1且未被标记过的点，则转（1）；否则结束，输出弧段集合。

通过上述步骤可以将轮廓从交点处分开。图1包括两个重叠椭圆，黑色点表示相交点，轮廓被分为四个曲线段，分别由四种颜色表示。图2所示为曲线弧分割应用于实际的椭圆印章图像效果图。

1.2.2 随机取点求椭圆参数

椭圆的一般方程为Ax2+Bxy+Cy2+Dx+Ey+1=0，椭圆参数与中心、长轴、短轴以及长轴倾角之间的关系见式（1）：

根据各弧段长度的比例，确定在每段弧上采样的次数，随机取点的次数与弧段长度成正比，每条弧段上随机取点的方法见表1所列。

由于椭圆包含5个未知参数，所以每次采样都要随机取5个非共线点。将这5个点（xi，yi）（i=1，2，3，4，5，6）带入椭圆一般方程，构建线性方程组（2），（3）及（4）：

其中，α=[A B C D E]T 。只有当系数矩阵对应的行列式|R|≠0时，原方程组才有唯一解，采用高斯消元法解方程组求出系数A，B，C，D，E，进而由式（1）求得中心、长短轴、长轴倾角以及离心率。若|R|=0，则重新采样。

1.2.3 确定椭圆位置

统计参数出现次數。椭圆累计函数定义如下：

2 系统测试与结果分析

基于集成开发环境Microsoft Visual Studio 2010，使用C++语言，应用微软基础类库MFC与文档-视图结构设计交互界面。类CmainFrame是系统的框架类，负责完成窗口布局管理，运用MFC类库中的CSplitterWnd类封装系统窗口所需功能，通过CreateStatic（）函数创建窗口，CreateView（）函数为每个窗口创建视图类CFormView。选择文件功能由类CFileDialog实现，ImageFileReader类对象接收文件的路径，完成图像读入，之后返回一个指向文件的指针。印章定位与配准系统整体界面如图4所示。

本文设计的椭圆印章自动定位系统中需要的图片通过扫描仪扫描得到。系统功能测试分为两部分，分别为预处理模块和椭圆印章定位模块。

（1）预处理功能模块

该模块主要用于提取输入图像中的红色分量，将图像灰度化、二值化并细化后得到骨架图。红色分量提取测试效果如图5所示。其中（a）为输入的RGB彩色印章测试图像，（b）为提取红色像素点后的效果图。将彩色图像灰度化并二值化，测试效果如图6所示。图像细化测试效果如图7所示。

预处理功能可去除测试图像中的无用信息，基于印章的颜色特性提取出有用信息，将彩色图像转化为二值图像，并得到细化的骨架图，减少图像存储空间，以便后续操作。从上述测试结果图可以看出，测试图像的背景较为复杂，含有不同颜色的文字图标，红色像素点除印章外，还包括图标、底纹等。点击相应按钮可以提取出原测试图中的所有红色像素点。二值图像较为准确地将图像像素点分为前景和背景。基于细化算法将二值图像转化为轮廓宽度为1的细化图像。

（2）印章定位功能模块

该模块的目标是计算出参数，基于细化的骨架图准确检测出椭圆印章在图像中的具体位置。椭圆印章定位测试效果如图8所示，印章在图中所示的方框区域内。

3 结 语

本文提出了椭圆印章自动定位方法，通过对系统各功能模块展开详细测试，验证该系统功能的正确性。系统能够有效提取测试图像中的红色分量，在灰度图像上定位出椭圆印章所在的具体位置，减小后续处理区域的面积，对于提高速度、简化算法具有重要意义，为印章真伪决策打下良好的基础，具有一定的应用价值。

参考文献

[1]魏兆兵，魏梦雅.企业印章管理中的法律风险防范[J].秘书之友， 2013， 4（7）： 12-13.

[2]赵雅丽.浅析单位印章的规范化管理[J].商场现代化， 2012，6（26）： 180.

[3]陈蕊丽.浅谈伪造印章的犯罪特点及防伪措施[J].中国品牌与防伪，2004，8（11）： 9-12.

[4]秦开怀，王海颍，郑辑涛.一种基于Hough变换的圆和矩形的快速检测方法[J].中国图象图形学报， 2010， 15（1）：109-115.

[5] PRASAD D K， LEUNG M K. Edge curvature and convexity base ellipse detection method[J]. Pattern recognition， 2012， 45（9）： 3204-3221.

[6]何瑾，刘铁根，周怡洁，等.基于边缘差异的印鉴自动鉴别[J].仪器仪表学报，2010，31（1）： 85-91.

[7] BASALAMAH S. Histogram based circle detection[J].International journal of computer science and network security，2012，12（8）： 40-43.

[8]张铮，王艳平，薛桂香，等.数字图像处理与机器视觉-Visual C++与Matlab实现[M].北京：人民邮电出版社，2014.

[9]何瑾.金融印鉴真伪识别新方法研究[D].天津：天津大学， 2010.

[10] BARWICK， SHANE D. Very fast best-fit circular and elliptical boundaries by chord data[J].IEEE Trans. Pattern analysis and machine intelligence，2009，31（6）： 1147-1152.

[11]李楠楠，卢荣胜，李帅.基于边界曲线弧分割的多椭圆检测[J].计算机应用，2011， 31（7）：1853-1855.