基于LIDAR点云回光强度信息的KNN算法与BP神经网络算法分类对比研究

梁宇乾 袁希平 甘淑

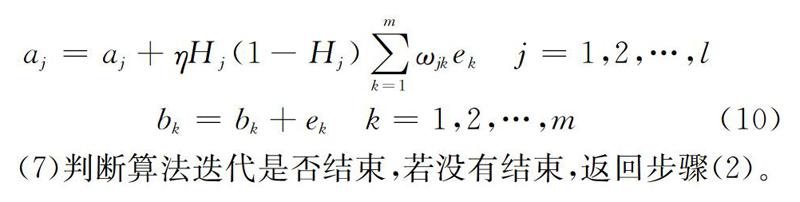
摘 要：机载LIDA点云数据中的回光强度信息可对地物进行精细分类。KNN算法和BP神经网络算法是目前比较热门的分类算法，在数据分类方面应用广泛，对这两种算法进行了分类比较研究。将回光强度信息作为训练样本，利用两种不同的方法进行分类。实验结果表明，BP神经网络在地物的精细分类以及边界线提取方面要优于KNN算法。

关键词：机载LIDAR；回光强度；KNN算法；BP神经网络；分类

DOI：10.11907/rjdk.172941

中图分类号：TP312

文献标识码：A 文章编号：1672-7800（2018）004-0077-05

Abstract：The light intensity information of airborne LIDA point cloud data can be classified on the ground objects.At present， there are many classification methods of intensity information.In this paper， two popular algorithms are classified and compared.KNN algorithm and BP neural network algorithm are popular classification algorithms， especially in data classification.This paper use light intensity information as the training samples for classification by two different methods.The experimental results show that BP neural network is better than KNN algorithm in fine classification of ground objects and extraction of boundary lines.

Key Words：airborne LIDAR； intensity； KNN algorithm； BP neural network algorithm； classification

0 引言

机载LIDAR即激光探测与测量，是集全球定位系统和惯性导航系统为一体的机载激光扫描，其所测数据为数字表面模型的离散点表示，数据中不仅含空间三维信息，还有入射角、GPS时、激光回光强度等信息。其中，回光强度大小与目标表面材质、入射光角度以及反射光角度都有关系。目前，LIDAR回光强度等信息越来越被重视，用回光强度提取空间信息的应用研究较多[1]。不同地物的反射强度不同，根据这一特性，可以利用回光强度对地物进行分类[2-3]。

分类是数据挖掘的核心和基础技术，在经营、决策、管理、科学研究等多个领域有着广泛应用。目前热门的分类技术有人工神经网络分类法、决策树分类法、KNN算法分类法等。KNN分类经过多年发展，已经成为一种简单、便捷、成熟、非参数的方法，广泛应用于文本分类、图像分类等多个领域，如沈泓等[4]学者通过K聚类的方法对数据进行整合。BP人工神经网络不仅具有自我学习能力，而且具有联想储存能力和寻找最优解能力，是时下最热门的一种分类方法，如顾亚风等[5]通过神经网络对古玩图片进行分类；茅千千[6]利用神经网络对石油项目进行综合评价。

1 KNN算法

最近邻算法是根据实例学习然后进行数据分类的一种最常用的方法。

令样本集D={x1`````xn}，在集合X中的每个样本xi类别已知。现有一个未知样本x，在集合X中有已知样本点x1，且x与x1距离最近，那么x的样本类型就与x1相同。

K最近邻算法（K-NearestNeighbor）是最近邻算法的变形应用。该算法将一个未知数据点n分类为与它距离最近的K个近邻点中个数最多且最近的那个类别。K最近邻算法从未知样本点n开始计算，不断扩大分类范围，直到包含进K个训练样本点结束，并把未知样本点n归为距离最近的K个训练样本点中出现频率最大的类别。一般测试样本与训练样本的距离使用欧式距离测量。图1和图2分别是KNN算法的一般流程和KNN算法使用步骤。

1.1 KNN中距离度量

在对数据进行挖掘和分析过程中需要知道数据间的差异，从而判断数据的相似性和类别。最常见的数据分析和挖掘方法是相关分析和分类、聚类算法。衡量个体差异的方法有很多，在KNN中分析数据相关性一般采取距离度量和相似度度量方法。

1.1.1 距离度量

在KNN算法中，未知数据与已知数据的相似性用距离判别，距离越大表示两个点越不相似。在KNN算法中基本的距离度量有3类：明可夫斯基距离、曼哈顿距离和欧式距离。

p值是一个变量，当p=2时就得到上述欧氏距离。

曼哈顿距离（Manhattan Distance）源于曼哈顿城市区块距离，是将不同维度上的距离进行求和后得到的結果。曼哈顿距离是明式距离的一种变形应用，当明氏距离p=1时得到距离度量公式：

切比雪夫距离（Chebyshev Distance）起源于国际象棋中国王的走法。我们知道国王每次只能往周围的8格中走一步，如果要从棋盘中A格（x1， y1）走到B格（x2， y2）最少需要走几步？扩展到多个维度空间，切比雪夫距离就是明式距离的一种变形应用，当明氏距离中p趋向无穷大时，有公式：

由此可见欧氏距离、曼哈顿距离和切比雪夫距离都是由明可夫斯基距离变形的另一种应用。

1.2 K值确定

在KNN算法中，所有的计算几乎都发生在分类阶段，而且分类效果的优劣主要体现在K值的选取上，所以取到合适的K值至关重要。如果K值数值偏小，得到的近邻数就会减少从而降低分类精度，同时提高了噪声对数据干扰；如果K值数值偏大，并且未知数据样本类型属于训练数据中包含数据较少的那一类，那么在用K值进行分类时，通常会把一些并不相似的数据包含进来，这样会使得噪声增加以及分类准确性降低。选取合适的K值一直是KNN的研究热点。

从图3可以看到有两个类型的样本数据，一类是正方形，另一类是三角形，而圆形是待分类的数据。如果K=3，离圆形距离最近的包含了2个三角形以及1个正方形，由于K值为3，于是圆形这个待分类点就属于三角形。如果K=5，那么圆形最近的有2个三角形和3个正方形，于是待分类点属于正方形。

K取值经验规则：

（1）K一般低于训练样本数的平方根。

（2）K是通过大量的样本数据进行测试、不同模型进行验证作出的最佳选择。

（3）当采用固定距离指标，那么K值可以提前确定，或者采用动态K值[10]。样本间类别不平衡时K值相对来说难以确定，朱响斌等[7]提供了K值的选择方法：当最近邻使用欧氏距离而且样本数据较大时，K的选择应当遵从：K→：∞，K/N→0[8-9]。普遍采取交叉验证法，评估最小错误率的K值作为最优K值[10-11]。

（4）如果给定训练样本中的类别个数是偶数，一般K会设置为一个奇数；如果类别个数为奇数，K通常设置为偶数。

2 BP神经网络

BP神经网络（Back Propagation）由以Rumelhart和McCelland为首的科学家小组于1986年提出，是一种逆向传播误差算法训练的多层前馈网络，也是目前应用最广泛的神经网络模型之一。

BP神经网络是多层前馈神经网络，该网络的主要特点是信号向前传递，误差逆向传播。在信号的前向传播中，输入的信号从输入层开始，经过隐含层逐层处理，直到输出层输出数据。每一层中的神经元（阈值大小）只影响下一层神经元。如果输出层得不到理想输出结果则进入逆向传播，根据所预测的误差调整网络的权值和阈值，从而使BP神经网络的预测输出不断向期望输出靠近。如图4所示，BP神经网络的结构模型包括输入层（input）、隐层（hide layer）和输出层（output layer）。

2.1 神经网络算法建立

基于机载LIDAR点云分类的BP神经网络算法建模包括BP神经网络构建、BP神经网络训练和BP神经网络分类，算法流程如图5所示。

2.2 神经网络训练过程

设X2，…，Xn是BP神经网络的输入值，Y1，Y2，…，Yn ωjk是BP神经网络的预测值， ωij和ωjk为BP神经网络权值。当神经网络输入节点数为n、输出节点数为m时，整个网络就表示一个从n个自变量到m个因变量的函数关系。

BP神经网络在做分类预测前首先要训练主动学习能力。BP神经网络训练步骤：

（1）网络初始化。根据分类所需类别以及输出结果种类，确定网络输入层节点数n、隐含层节点数1、输出层节点数m，对输入层、隐含层和输出层进行初始化处理，各个神经元之间的连接权值ωij，ωjk，初始化隐含层阈值a，输出层阈值b，给定神经元激励函数以及学习速率。

（2）隐含层输出计算。根据输入向量X、输入层和隐含层间连接权值ωij以及隐含层阈值a，计算隐含层输出H：

（7）判断算法迭代是否结束，若没有结束，返回步骤（2）。

3 分类结果与对比研究

试验区为云南某湖泊的滩涂机载LIDAR点云数据，图6是该区域的平面点云图。由这幅点云图把该区域大致分为两类：水域点和陆地点。图中蓝色点为已知水域点，棕色点为陆地点，灰色点代表未分类的点云数据（如需看彩图，请与编辑部联系）。

3.1 KNN分类

首先，该区域的点云数量约为10万个，选取已知类型的8 000个点为训练数据。其次，通过多次实验取K值。表1是K值大小与测试集准确率间的关系。由表1可以看出，K值取15时测试集的准确率最高。随着K值的增加，测试集的准确率逐步下降。图7为该实验区KNN算法分类效果。

3.2 BP神經网络分类

用已知分类点进行训练并且进行数据测试，图8是神经网络在训练数据过程中迭代次数和训练误差的关系。由图8可以看出，随着迭代次数的增加，训练误差迅速下降，在第6次迭代趋于平稳，但仍有下降趋势，误差无限趋近于0.1。

图9是通过BP神经网络分类后得到的点云分类效果。从图中可以看到，通过BP网络分类可以有效区分陆地点和水域点。在水域点中有部分点云数据是算法中认为的陆地点，造成这种情况原因的是因为水域较浅，机载LIDAR的激光束穿透能力很强，激光束穿透水面打到水面底部岩石或土地上，造成分类错误。

3.3 对比研究

通过图10和图11对比发现，KNN算法和BP神经网络算法都能较好地将点云绝大部分的地面点和水域点分开，但是通过对比发现有以下3点可以看出KNN算法和BP神经网络算法的不同[9-10]：

（1）两幅图中红框所标注出的1区、3区、4区，KNN算法不能很好判别，把一些地面点判别为水域点。虽然神经网络也出现类似情况，但是通过比较发现，BP神经网络的分类更为精细。

（2）对于2区来说，KNN算法的分类效果好于BP神经网络，BP神经网络会把一些明显的水域点判别为地面点。这里有两个原因：①KNN算法是通过近邻点分类；②由于机载LIDAR的激光束穿过水面，直接打在了水底造成了误分类。

（3）在区分地物边界方面，BP神经网络显然比KNN算法更出色。通过对比不难看出，KNN算法对明显的边界不能很好地区分。

4 结语

通过该实验对比发现，BP神经网络算法在分类方面比KNN算法更为精细，尤其表现在对边界线的提取方面。这取决于BP神经网络利用积极学习的方法，拥有自动学习能力，并且能充分逼近复杂的非线性关系。反观KNN算法，其采用懒惰学习方法，导致对拥有海量数据和类别多的数据不能实现很好的分类。

参考文献：

[1] ACKERMANN F. Airborne laser scanning-present status and future expectation[J].ISPRS Journal of Photogrammetry & Remote Sensing，1999（54）：64-67.

[2] 左志权.顾及点云类别属性与地形结构特征的机载LiDAR数据滤波方法[D].武汉：武汉大学， 2011.

[3] 贾广帅.机载激光雷达数据特点和滤波方法研究[D].青岛：山东科技大学，2007.

[4] 沈泓，刘顺.基于K-means聚类算法的数据分析模型应用研究[J].软件导刊，2017，16（3）：103-107.

[5] 顾亚风，叶学义.基于卷积神经网络的古玩图片分类方法[J].软件导刊，2017，16（5）：174-178.

[6] 茅茜茜.BP神经网络在石油项目经济效益综合评价中的应用[J].软件导刊，2017，16（4）：145-148.

[7] 朱响斌.一种基于八叉树的三维实体内部可视化技术[J].中国图象图形学报，2002，7（3）：229-233.

[8] LOFTSGAARDEN D O， QUESENBERRY C P.A nonparametric estimate of multivariate density function[J].Ann Math Statist，1965，36（3）：1049-1051.

[9] COVER T M，HART P E.Nearest neighbor pattern classification[J].IEEE Trans Inform Theory，1968，13（1）：21-27.

[10] LACHENBRUCH P A，MICKEY M R.Estimation of error rates in discriminant analysis[J].Technometrics，1968，10（1）：1-11.

[11] STONE M. Cross validation： a review， math operationsforschung und statist[J].Series Statistics，1978，9（1）：127-139.

（責任编辑：杜能钢）