磁悬浮高速电机系统建模与控制

张涛 刘欣凤 莫丽红 倪伟 桑英军 丁卫红

摘 要：为实现磁悬浮电机的稳定悬浮运行，研究一种基于最优控制理论的控制器设计策略。在分析磁悬浮电机结构和工作原理的基础上，建立悬浮转子的运动方程，构建以气隙偏移量和控制电流为状态变量的系统状态方程，经线性化处理后，采用最优控制理论，设计闭环控制器。构建闭环系统仿真与试验平台并进行仿真与试验研究，测量径向位移和转子几何中心运动轨迹波形。仿真和实验研究结果表明，基于最优控制理论的闭环控制器可实现磁悬浮电机的稳定悬浮运行，并具有较好的动静态性能。

关键词：高速电机；磁悬浮电机；磁轴承；状态方程；最优控制

中图分类号：TM 301.2

文献标志码：A

文章编号：1007-449X（2018）04-0098-07

Abstract：To realize the stable suspension operation of magnetic suspension motor， a controller design algorithm is presented using the optimal control theory. Based on analyzing the structure and operation principle of the magnetic suspension motor， the motion equation of suspension rotor was built， and then the state equation was established by taking air gap offset and control current as state variables. This state equation was further linearized and thus the linear optimal control theory can be applied to design the closed-loop controller. To show the effectiveness of the presented method， the simulation and experimental research were carried out. The experimental and simulation results show that the designed controller can realize the high-speed suspension operation of magnetic levitation motor with good dynamic and static performances.

Keywords：high speed motors； magnetic suspension motors； magnetic bearing； state equation； optimal control

0 引 言

由于高转速，高速电机的体积远小于同等功率的中、低速电机。高速电机具有：高功率密度，节约材料，减小设备体积与重量；可直接驱动负载，无需传动机构，无传动损耗和噪声，效率高；转子转动惯量小，动态响应速度快等一系列优点。高速电机在离心压缩机、航空航天、高速电主轴、新能源等高速直接驱动领域具有广阔的应用前景，目前已成为电气工程领域的研究热点[1-3]。

磁轴承支承技术解决了高速电机转子—轴承系统存在的摩擦和磨损问题，可大幅度提升电机转速和输出功率，但是由多个磁轴承单元构成的磁轴承—转子系统为多变量、强耦合的非线性复杂系统，其动、静态性能主要取决于所采取的闭环控制策略。目前，磁悬浮轴承的闭环控制系统设计主要是通过研制性能优良的控制器，使得磁悬浮转子在物理极限内使刚度、阻尼与磁轴承的工作环境、运行状态及转速相适应，并通过优化设计闭环控制算法及前馈补偿环节来提高转子的回转精度，方法主要有H∞、逆系统、滑模变结构、神经网络逆控制等。这些算法复杂，计算量大，难以实现工程应用[4-5]。

本文以磁轴承支承的五自由度高速电机为研究对象[6-7]，以实现磁轴承转子稳定悬浮并提高磁轴承支承的高速电机系统动态性能和运行可靠性为目标，建立以气隙偏移量和控制电流为状态变量的悬浮转子状态方程，经过线性化处理后，采用最优控制理论设计磁轴承状态变量最优控制器，并进行仿真及实验研究[8-10]。

1 磁悬浮电机数学模型

磁轴承支承的高速电机结构如图1所示，转子由高速电机单元驱动旋转，两端分别采用一个磁轴承单元控制径向两自由度，轴向采用单自由度磁轴承控制，2个径向磁轴承共包含8个电磁线圈，其输入电压分别为e1、e2、e3、e4、e5、e6、e7、e8；对应位置的气隙长度分别为g1、g2、g3、g4、g5、g6、g7、g8；每个控制线圈产生的电磁吸力分别为F1、F2、F3、F4、F5、F6、F7、F8；轴向磁轴承产生的电磁力为Fz+、Fz-。由径向和轴向位移传感器检测转子径向与轴向位移，建立位移闭环控制系统。通过调节线圈电流，对转子施加与偏心位移相反的电磁力，将转子拉回平衡位置，实现转子稳定悬浮。

图2（a）给出的坐标系OXsYsZs是以传感器几何中心为轴线的定子坐标系，图2（b）给出的坐标系GXrYrZr是以转子几何中心为轴线的转子坐标系，磁轴承对转子的控制目标是让转子坐标系渐进定子坐标系，最终让转子坐标系与定子坐标系重合。转子坐标系相对于定子坐标系的夹角分别为θx、θy、θz；轉子受到的悬浮力分量分布为Fx、Fy、Fz；角速度分量为ωx、ωy、ωz；线速度分量为vx、vy、vz；转矩分量为Tx、Ty、Tz；质心G在定子坐标系中的坐标为（x0，y0，z0）。

4 控制器设计

基于最优控制理论的悬浮转子控制系统如图3所示，虚线部分为系统描述的磁悬浮轴承模型，变量r和u分别为参考输入信号和控制输出信号，y是以气隙长度为变量的输出矢量，K1和K2分别为反馈系数矩阵，本控制系统为4输入和4输出系统。

5 仿真和实验结果

为验证模型和控制策略的正确性，建立如图3所示的控制系统并进行仿真研究，磁悬浮电机主要参数为：l=0.28 m，转子质量为m=1.85 kg，Jz=6.12×10-4 kg·m2，Jx=Jy=4.54×10-4 kg·m2，磁轴承绕组电阻为2.68 Ω，电感为0.257 H，平均气隙长度为1 mm，电机运行最高转速为20 000 r/min。

圖4所示的是当转子转速为20 000 r/min稳定悬浮运行时，在转子端施加1 N的阶跃力的气隙偏移量瞬态波形，从仿真结果可以看出，经过0.15 s，转子在磁轴承的控制下，重新回到平衡位置，y方向的气隙偏移量远大于x方向的气隙偏移量。

图5给出系统在最优控制策略与传统PID控制策略下的响应曲线。与传统PID控制策略相比，最优控制策略下的系统响应具超调更小、调节响应时间更短。

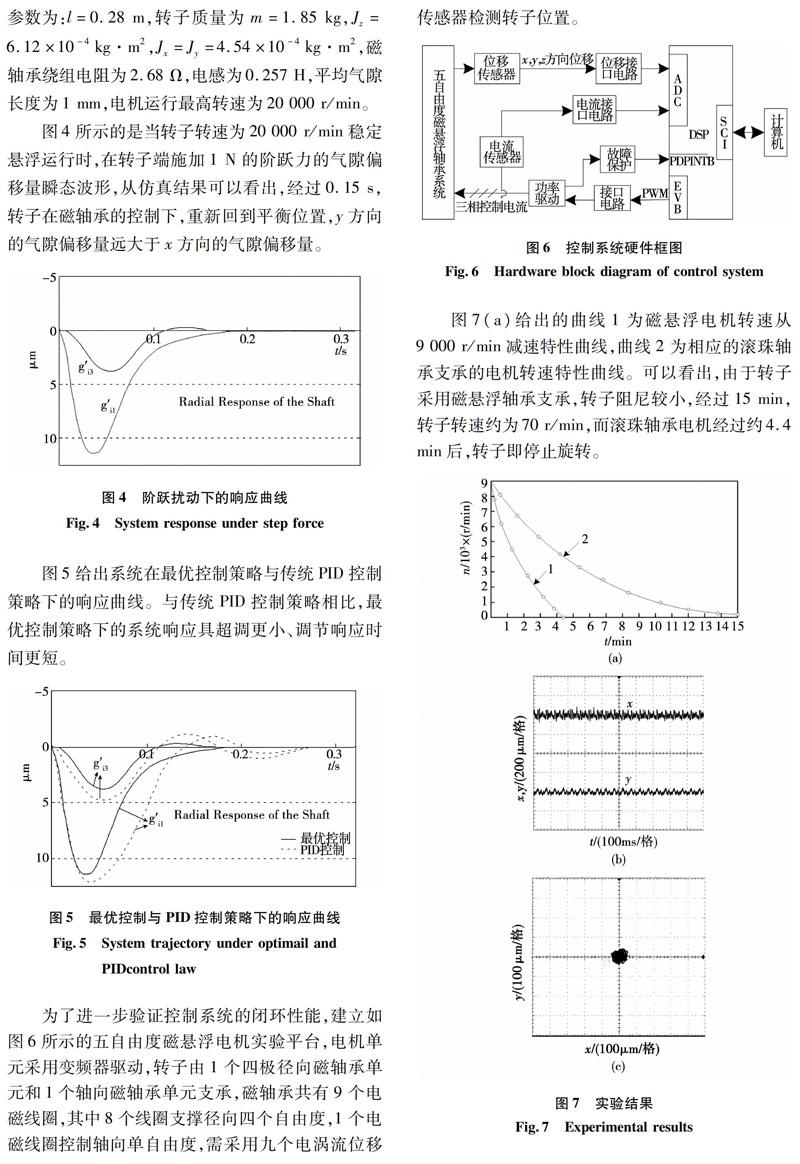
为了进一步验证控制系统的闭环性能，建立如图6所示的五自由度磁悬浮电机实验平台，电机单元采用变频器驱动，转子由1个四极径向磁轴承单元和1个轴向磁轴承单元支承，磁轴承共有9个电磁线圈，其中8个线圈支撑径向四个自由度，1个电磁线圈控制轴向单自由度，需采用九个电涡流位移传感器检测转子位置。

图7（a）给出的曲线1为磁悬浮电机转速从9 000 r/min减速特性曲线，曲线2为相应的滚珠轴承支承的电机转速特性曲线。可以看出，由于转子采用磁悬浮轴承支承，转子阻尼较小，经过15 min，转子转速约为70 r/min，而滚珠轴承电机经过约4.4 min后，转子即停止旋转。

图7（b）所示的是转速为9 000 r/min时的x和y方向位移曲线，转子径向位移振幅约为38 μm，相对应的转子几何中心轨迹如图7（c）所示，从实验结果可以看出，基于最优控制理论的磁悬浮高速电机可实现转子稳定悬浮运行。

6 结 论

分析了五自由度磁悬浮高速电机结构与工作原理，推导了悬浮转子运动方程，建立以转子气隙偏移量和控制电流为状态变量的系统状态方程，线性化处理后，采用最优控制理论设计了磁悬浮高速电机最优控制器，并进行仿真和实验研究，仿真和实验结果表明，本文设计的控制器可实现磁悬浮高速电机转子稳定悬浮运行，并具有较好的动、静态性能。

参 考 文 献：

[1] 王凤翔. 高速电机的设计特点及相关技术研究[J]. 沈阳工业大学学报， 2006， 28（3）：258.

WANG Fengxiang. Study on design feature and related technology of high speed electricalmachines[J]. Journal of Shenyang University of Technology， 2006， 28（3）： 258.

[2] 张凯， 戴兴建， 张晓章. 磁轴承超临界高速电机系统控制器设计[J].清华大学学报学报（自然科学版）， 2010， 50（11）： 1785.

ZHANG Kai， DAI Xingjian， ZHANG Xiaozhang. Controller design of a supercritical high speed motor system suspended by active magnetic bearing[J]. Journal of TsingHua University（Science and Technology）， 2010， 50（11）： 1785.

[3] 张涛， 朱熀秋， 孙晓东， 等. 基于有限元法的高速永磁转子强度分析[J]. 电机与控制学报， 2012， 16（6）： 63.

ZHANG Tao， ZHU Huangqiu， SUN Xiaodong， et al.Strength analysis on high-speed permanent magnet rotor using finite element method[J]. Electric Machines and Control， 2012， 16（6）： 63.

[4] 张涛， 朱熀秋， 孙晓东， 等. 基于双重傅里叶变换的永磁转子涡流损耗分析[J]. 江苏大学学报（自然科学版）， 2013， 34（1）： 66.

ZHANG Tao， ZHU Huangqiu， SUN Xiaodong， et al. Rotor eddy current loss analysis of permanent magnet rotor based on double Fourier transforms[J]. Journal of Jiangsu University （Natural Science Edition）， 2013， 34（1）： 66.

[5] 张涛， 朱熀秋， 孙晓东， 等. 基于涡流损耗分析的永磁型无轴承电机优化[J]. 电机与控制学报， 2012， 16（10）： 58.

ZHANG Tao， ZHU Huangqiu， SUN Xiaodong， et al. Optimization of permanent magnet type bearingless motor using eddy current loss analysis[J]. Electric Machines and Control， 2012， 16（10）： 58.

[6] XU Yanliang， DUN Yueqin， WANG Xiuhe， et al. Analysis of hybrid mganetic bearing with a permanent magnet in the rotor by FEM[J]. IEEE Transactions on Magnetics， 2006， 42（4）： 1363.

[7] Phyo Phyo San， Beibei Ren， Shuzhi Sam Ge， et al. Adaptive neural network control of hard disk drives with hysteresis friction nonlinearity [J]. IEEE Transactions on Control System Technology， 2011， 19（2）： 351.

[8] Alexander Lanzon， Panagiotis Tsiotras. A combined application ofH∞ loop shaping and μ-synthesis to control high-speed flywheels [J]. IEEE Transactions on Control System Technology， 2005， 13（5）： 766.

[9] FANG Jiancheng， REN Yuan. Decoupling control of magnetically suspended rotor system in control moment gyros based on an inverse system method [J]. IEEE Transactions on Magnetics， 2012， 17（6）： 1133.

[10] LIN F J， CHEN S Y， HUANG M S. Intelligent double integral sliding-mode control for five-degree-of-freedom active magnetic bearing system [J]. IET Control Theory and Applications， 2010： 1287.

（編辑：刘素菊）