Analytical approach to entropy generation and heat transfer in CNT-nanofluid dynamics through a ciliated porous medium ＊

Noreen Sher Akbar , M. Shoaib , Dharmendra Tripathi , Shashi Bhushan , O. Anwar Bég

1. DBS&H, CEME, National University of Sciences and Technology, Islamabad, Pakistan

2. School of Natural Sciences, National University of Sciences and Technology, Islamabad, Pakistan

3. Department of Mechanical Engineering, Manipal University, Jaipur, India

4. Medical, Energy and Propulsion Engineering Sciences, Department of Aeronautical and Mechanical Engineering, University of Salford, Newton Building, Manchester, M54WT, UK

Introduction

In recent decades, nanofluids have been receiving extensive attention in science, engineering, medicine(targeted drug delivery) and industry owing to their enhanced thermal conductivity and heat transfer characteristics which contribute to their improved performance in for example heat exchangers, cooling devices, solar collectors and pharmacological treatments. Nanofluids are fabricated by dispersing of nanoparticles (Al2O3, CuO, TiO2, CNT etc.) in base fluids, such as water, ethylene glycol, and oil etc.Some investigators[1-3]have considered carbon nanotubes (CNT) in synthesizing the nanofluids due to its high thermal conductivity in comparison with other nanoparticles. Carbon nanotube (CNT) is an allotrope of carbon. They take the form of cylindrical carbon molecules and have novel properties that make them potentially useful in a wide variety of applications in nanotechnology, electronics, optics and other fields of materials science. CNTs are implemented in various geometrical configurations, e.g., as single-wall CNT,double-wall CNT and multi-wall CNT. Xie and Chen[4]have reviewed progress in preparation techniques and also experimental and theoretical studies relating to heat transfer characteristics of CNT-nanofluids and concluded that thermal conductivity of CNTs, interfacial thermal resistance between the CNT and the matrix, and dispersion status of the CNTs in the base fluid have significant effects on the thermal transport in CNT-nanofluids due to the complex morphologies and surface chemistry of the suspended CNTs. Another review on CNT-nanofluids has been presented by Murshed and De Castro[5], wherein it was concluded that nanofluids containing MWCNTs are found to exhibit higher conductivity and heat capacity compared to base ionic liquids. Recently,much attention has been focused on the study of CNT-nanofluids: representative investigations in this regard include the works of Halelfadl et al.[6], Saida et al.[7],Hordy et al.[8], Yadav et al.[9], Walvekara et al.[10],Xing et al.[11]and Jiang et al.[12]. These articles have elaborated upon the efficiency, stability and thermophysical properties of CNTs.

In parallel with the above developments,significant interest has also grown in engineering designs inspired by nature i.e., biomimetics and bionics. One very intriguing example in this area is the use of “artificial cilia” to create pumping and/or mixing in microfluidic devices. A very interesting review has been done by Den Toonder and Onck[13]in which it has been highlighted that cilia may be implemented successfully in (fluid) actuation and sensing operations. Microscopic actuators resembling cilia have been shown to be actuated to move under the influence of various stimuli such as electrostatic field, magnetic field, and even light and mixing in microfluidic environments. Artificial cilia are also applicable in engineering lab-on-a-chip devices and compliant surface control designs in aeronautics and hydronautics. Blake[14]presented a model for the micro-structure in ciliated organisms and observed that cilia propel a relatively larger volume of fluid during the effective stroke when compared with the recovery stroke, and therefore create a net fluid transport in the direction of the effective stroke.Khaderi et al.[15]investigated the breaking of symmetry in microfluidic propulsion driven by artificial cilia, Khaderi et al.[16]reported on numerical simulations of microfluidic propulsion by the metachronal beating of magnetic artificial cilia.Khaderi et al.[17]extended their earlier work to consider fluid-structure-interaction (FSI) effects in three-dimensional magnetic artificial cilia dynamics.

The above studies were confined to purely hydrodynamic aspects. In many recent developments,engineers have also explored heat and mass diffusion in biomimetic systems. With the presence of heat transfer, entropy generation minimization becomes a major consideration since it is intimately associated with the maximum achievable thermal efficiency of a system and therefore thermodynamic optimization.The break-through work in this area was conducted by Bejan[18], who considered entropy generation in convective heat transfer for different flow configurations: pipe flow, boundary layer over flat plate, single cylinder in cross-flow and flow in the entrance region of a flat rectangular duct. He derived a non-dimensional number (now termed the Bejan number) which is the ratio of the entropy generation due to the heat transfer to the total entropy generation.Bejan[19]further extended his study to counter flow heat exchangers for gas-gas applications in chemical and mechanical power generation. Bejan[20]also introduced the new thermodynamics of finite-size devices and finite-time processes for minimizing entropy generation, an area which is now usually termed second law thermodynamic analysis.Abu-Qudais et al.[21]presented a numerical analysis on entropy generation in free convection external to a horizontal pipe. Baytaş[22]incorporated the Darcy’s law in his study and discussed the entropy generation for natural convection in an inclined porous medium cavity. Makinde and Bég[23]investigated analytically with Hermite-Pade expansions, the influence of chemical reaction on magneto-hemodynamic blood flow with entropy generation. Rashidi et al.[24]used a genetic algorithm and neural dynamics to assess the relative performance via entropy generation minimization of trans-critical biomimetic thermodynamic cycles. Rashidi et al.[25]further explored thermodynamic optimization and entropy generation minimization in Joule-Thomson cycles of relevance to spacecraft propulsion systems. Bég et al.[26]used a differential transform method to compute the propulsion efficiency of swirling magnetic disk nuclear engines, evaluating in detail the effect of Bejan number and entropy generation minimization via second law methods. Rashidi et al.[27]have analysed entropy generation minimization in magnetized blood flow with wall mass flux effects as a simulation of entropy generation in capillary transport. Further studies deploying entropy generation methods include Öztop et al.[28](for convection in ducts), Dağtekin et al.[29](for heat transfer in ducts with longitudinal fins), Dağtekin et al.[30](for free convection in gamma-shaped enclosures), Basak et al.[31](for heat transfer in a trapezoidal cavity), Guelpa et al.[32](for latent thermal energy harnessing) and Anand[33](for non-Newtonian slip flow and heat transfer in microchannels). Akbar[34]recently studied entropy generation in heat transfer and peristaltic magneto hydrodynamic flow. Ellahi et al.[35]considered entropy generation in copper-water nanofluid heat transfer. Further studies include Ellahi et al.[36], Akbar et al.[37], Ellahi et al.[38]and Sheikholeslami et al.[39], these articles addressing different types of nanoparticles and different body force effects. Nadeem and Sadaf[40]present theoretical analysis of Cu-blood nanofluid for metachronal wave of cilia motion in a curved channel.

In the aforementioned works, thus far no consideration of the collective effects of CNT-nanofluids, entropy generation and cilia motion, has been made. This constitutes an important problem which has substantial potential applications in thermodynamic and hydromechanical optimization of nano-/micro-fluidic devices exploiting artificial cilia.This is the focus of the present work wherein we develop a mathematical model to study the entropy generation, heat and mass transfer and metachronal wave propulsion due to beating cilia (applicable),References, and Appendices (where applicable)follow the Conclusions.

1. Nanofluid flow driven by cilia beating

We consider heat transfer in incompressible Newtonian CNT-nanofluid flow through a circular tube containing an isotropic, homogenous and sparsely-packed porous medium. Wall slip is present.Entropy generation is also present. The inner surface of the circular tube is flexible and ciliated with Metachronal waves and the flow occurs due to collective beating of cilia. We represent the geometry of the problem in a cylindrical coordinate systemas depicted in Fig.1.

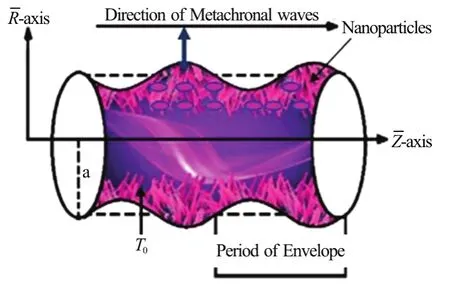
Fig.1 (Color online) Geometry of Metachronal propulsion of nanofluids by beating cilia

In this study, we adopt the well-known envelope approach[14-17]where the ciliary tips are assumed to move in elliptical paths, e.g.

whereadenotes the radius of tube,is a measure of the cilia length, λ andcstand for wavelength and wave speed of the metachronal wave, α is a measure of the eccentricity of the elliptical motion andis some reference position of the wall particles.

If the no slip condition is applied, then the velocities of the transporting fluid are just those ca[u1s4-e1d7]by the cilia tips, which can be formulated as:

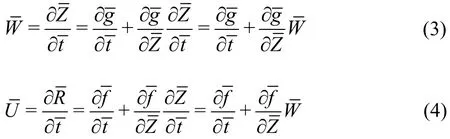
Using Eqs.(1), (2) in Eqs. (3), (4), the velocity components are obtained as:

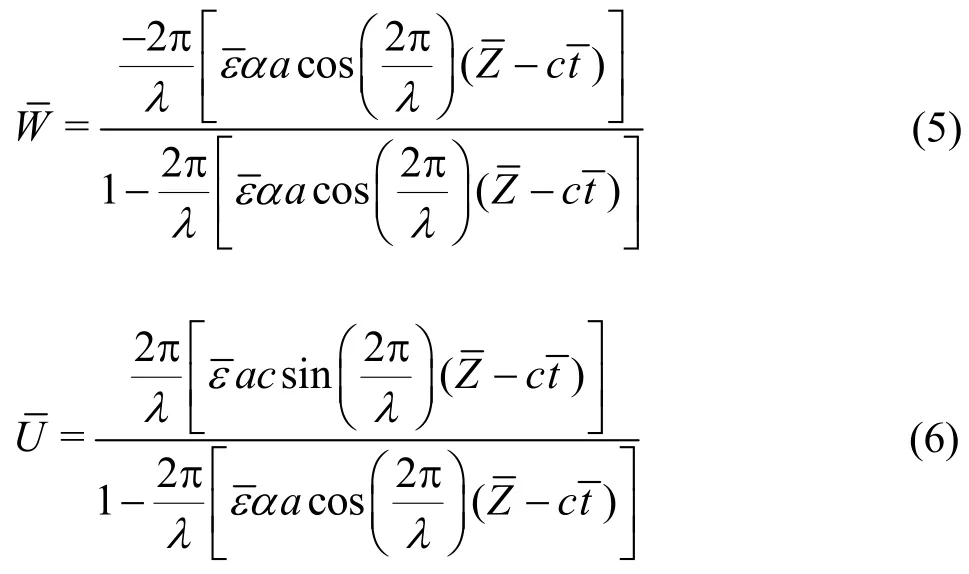
whereandbe the axial and the radial velocities of the cilia respectively. The transformations between the laboratory and wave frames which facilitate a solution of the moving boundary value problem are:

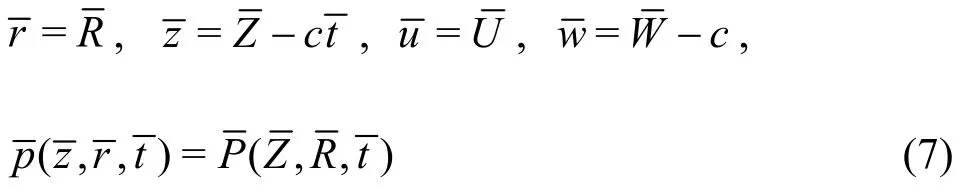
whereis pressure. In the moving coordinates system (,), the flow between the two tubes is unsteady, it becomes steady in a fixed frame (,)moving with the same speed as the wave moves in the-direction.

2. Governing equations and analytic solutions

The governing equations for incompressible CNT-nanofluid flow through a homogenous, isotropic,non-deformable, sparsely packed (high permeability)porous medium in the absence of gravity force(gravity effects vanish for a horizontal tube) may be posed as follows:

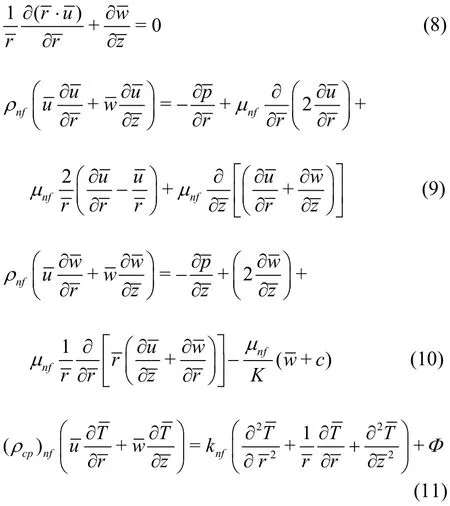
whereandare the radial and axial coordinates,andare the velocity components in theanddirections respectively,Kis permeability of the porous medium,is the local temperature of the fluid and Φ is the viscous dissipation term. Further,ρnfis the effective density, μnfis the effective dynamic viscosity, (ρcp)nfis the heat capacitance,αnfis the effective thermal diffusivity, andknfis the effective thermal conductivity of the nanofluid,which are defined as:

where φ, ρf, ρs, μf, (ρcp)nf, (ρcp)s,kfandksare volume fraction of the carbon nanotube,density of base fluid, density of carbon nanotube,viscosity of base fluid, heat capacitance of base fluid,heat capacitance of carbon nanotube, thermal conductivity of base fluid, and thermal conductivity of carbon nanotube. Proceeding with the analysis, to facilitate analytical (and computational) solutions, we introduce the following non-dimensional quantities:

The boundary conditions are imposed as:

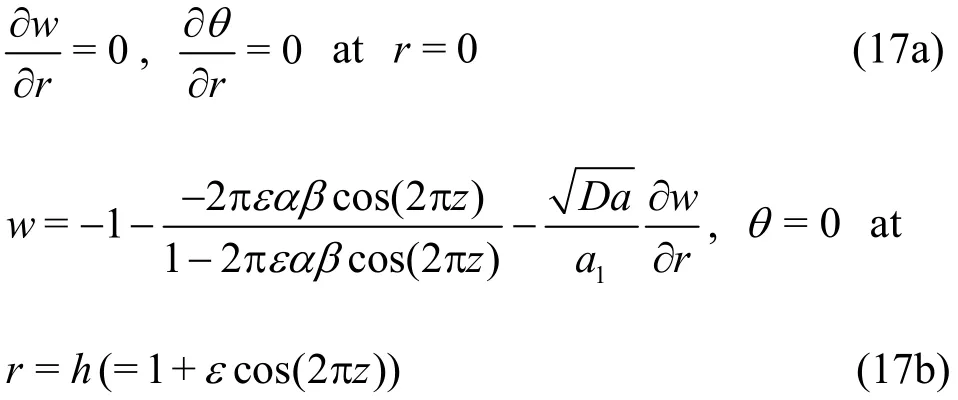
wherea1is hydrodynamic slip parameter. Solving Eqs. (14)-(16) together with the boundary conditions in Eqs. 17(a), 17(b), the solution for the axial velocity emerges as

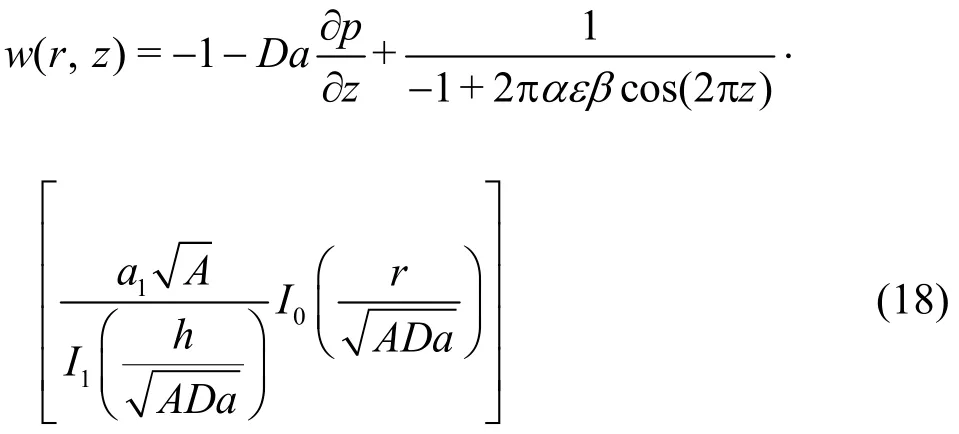
The solution for the temperature field is found to be

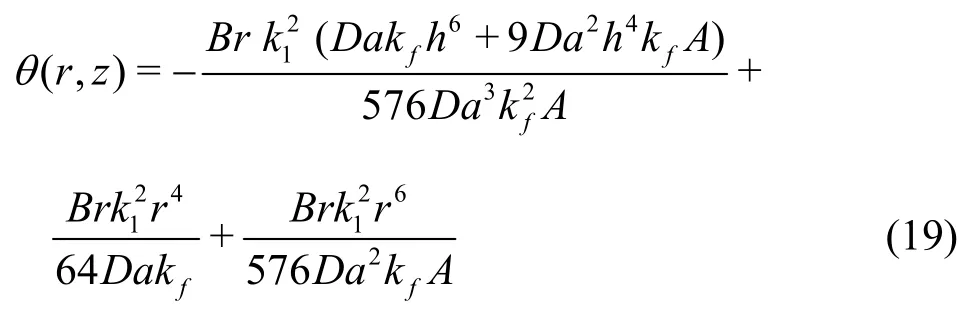
whereI0andI1are modified Bessel functions of the first kind of zero and first order, respectively, and

The volumetric flow rate is defined as

The relationship between volumetric flow rate in both frames of reference (moving and fixed) is expressed as

Using Eqs. (18), (21), the pressure gradient is obtained as

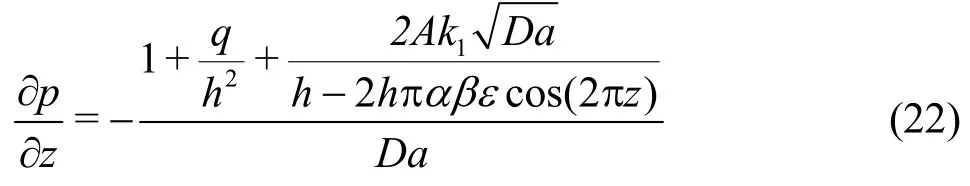
The pressure difference across one wavelength is further defined as

3. Entropy generation

The viscous dissipation term (）(see for example Refs. [18-29]) is defined as

Volumetric entropy generation is given by

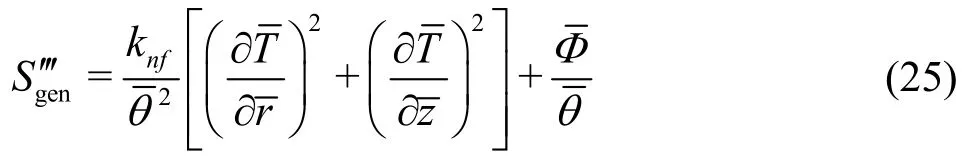
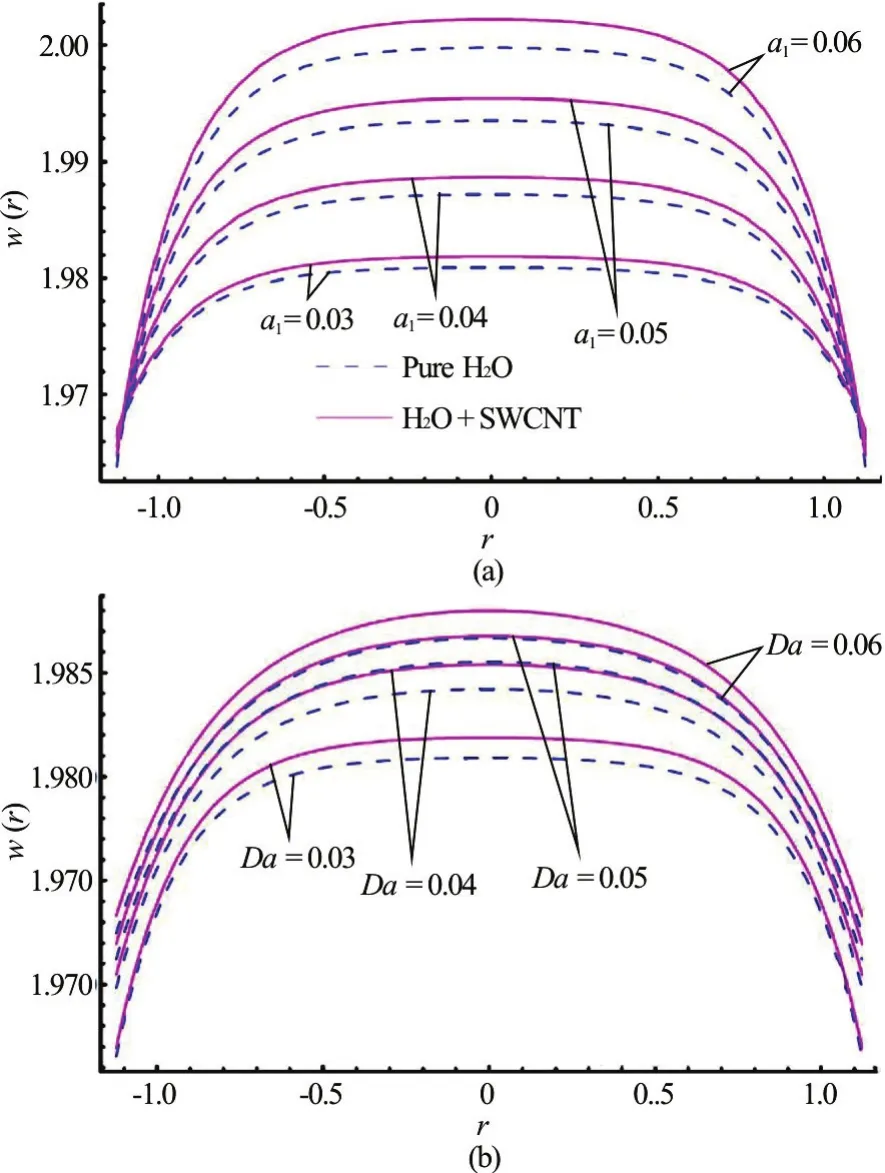
Fig.2 (Color online) Velocity profiles (axial velocity against the radial coordinate) for different values. Other parameters are fixed i.e., α=0.2, ε=0.4, β=0.2,Q=-2.5

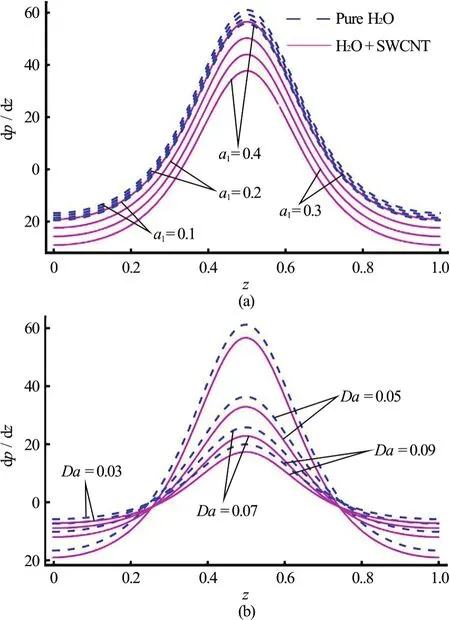
Fig.3 (Color online) Pressure gradients along the tube length for different values. Other parameters are fixed i.e.,α =0.3, ε=0.4, β=0.2, Q=-0.5

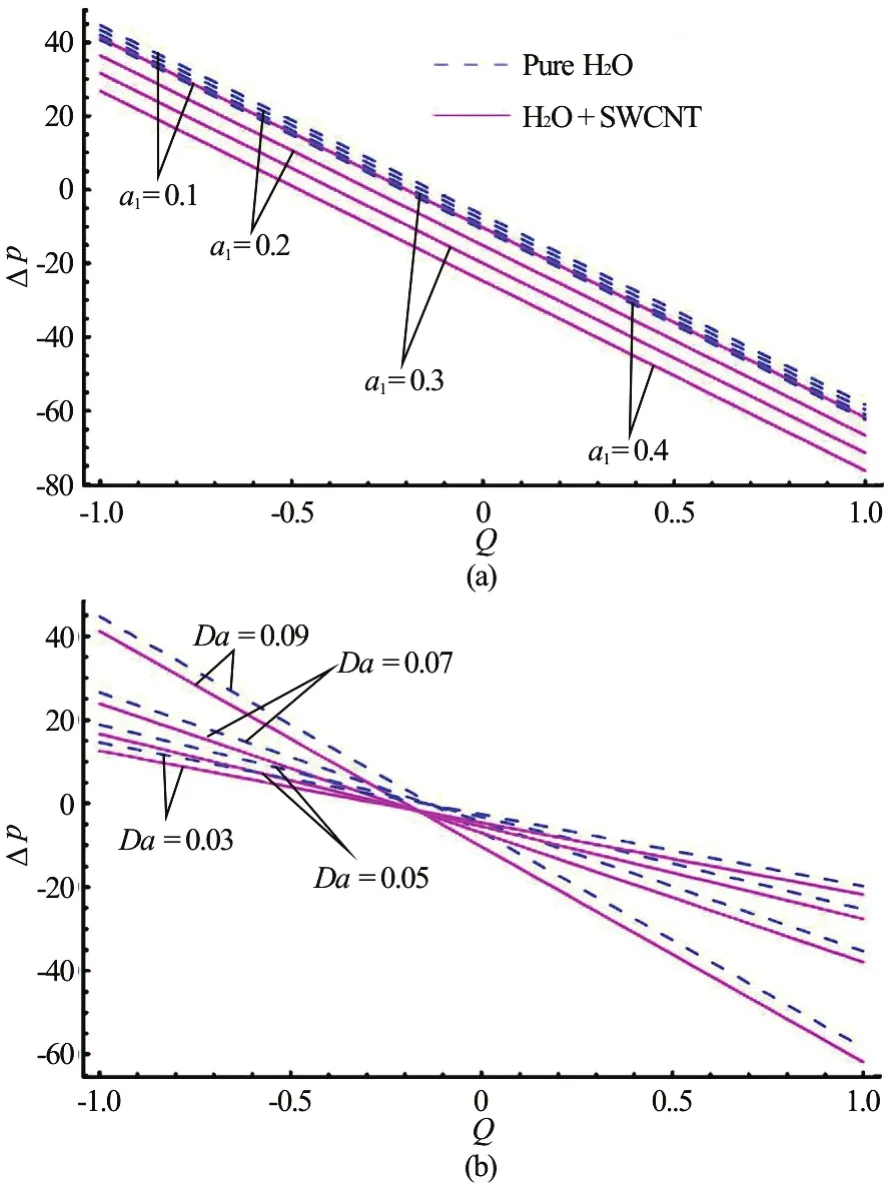
Fig.4 (Color online) Pressure rises against the flow rate for different values. Other parameters are fixed i.e.,α= 0.3, ε=0.4, β=0.2, Q=-0.5

Entropy generation in non-dimensional form is given as

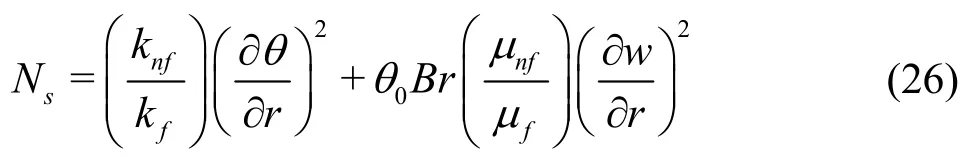
where θ0=/Hereis dimensional temperature at the wall andis non-dimensional temperature at the wall (andrefer to dimensional and non-dimensional temperatures,respectively). Equation (26) consists of two parts, in which the first part is the entropy generation due to finite temperature difference (Nscond) and the second part is the entropy generation due to viscous effects(Nsvisc). The Bejan number[18]is defined as

which may further be expressed in the form

Fig.5 (Color online) Temperature profiles (temperature against the radial coordinate) for different values. Other parameters are fixed i.e., a1 =0.04, ε=0.4, β =0.2,φ= 0.3, Q=2.5

The Bejan number is clearly a function of the Brinkman number (Br). AsBrincreases, the entropy generation due to fluid friction irreversibility increases in the system. Irreversibility mechanism domination is an important aspect of entropy generation analysis but the volumetric entropy generation does not provide any information regarding this. The Bejan number (Be) has been introduced in modern second law thermodynamic analysis to overcome this shortcoming. The Bejan number embodies the ratio of entropy generation which is caused through heat transfer to the total entropy generation.

4. Numerical results and discussion

In this section, the graphical explanation of the analytical expressions for velocity, temperature,pressure gradient, pressure rise, entropy generation,Bejan number and streamlines is expressed with respect to certain changes in the physical parameters through illustrations (Figs. 2-11). A comparative study for pure water and SWNT-water is also depicted through the numerical results.

Fig.6 (Color online) Bejan numbers against the radial coordinate for different values. Other parameters are fixed i.e.,a1 =0.04, ε=0.4, β=0.2, φ=0.3, Q=2.5

Figures 2(a), 2(b) represent the changes in the fluid axial velocity profiles with respect to slip parameter (a1) and Darcy number (Da). It is observed that velocity is directly proportional to both the physical parameters. As slip parameter increases the adherence of the fluid to the tube walls decreases.This leads to acceleration in axial flow. With greater Darcy number, the Darcian porous drag force (i.e.,bulk drug effect due to porous media solid fibers) is reduced. Larger Darcy numbers correspond to a greater permeability in the porous medium which implies a lesser concentration of solid fibers. The increase in permeability aids percolation of fluid and this manifests in axial flow acceleration i.e. a rise in the magnitude of axial velocity. In both Fig.2(a), the axial velocity,w(r), attains its maximum values at the center of the tube and decreases near the boundary of the tube. We also note that the change in the velocity profile with respect to is greater as compared toDa.This demonstrates that hydrodynamic wall slip exerts a greater influence than porous medium permeability on the axial flow. It is further revealed that the variation in velocity profile for SWCNT-nanofluids is more than pure water at fixed values of other parameters.

Figures 3(a), 3(b) illustrate the evolution of pressure gradient with axial tube length. It is evident that

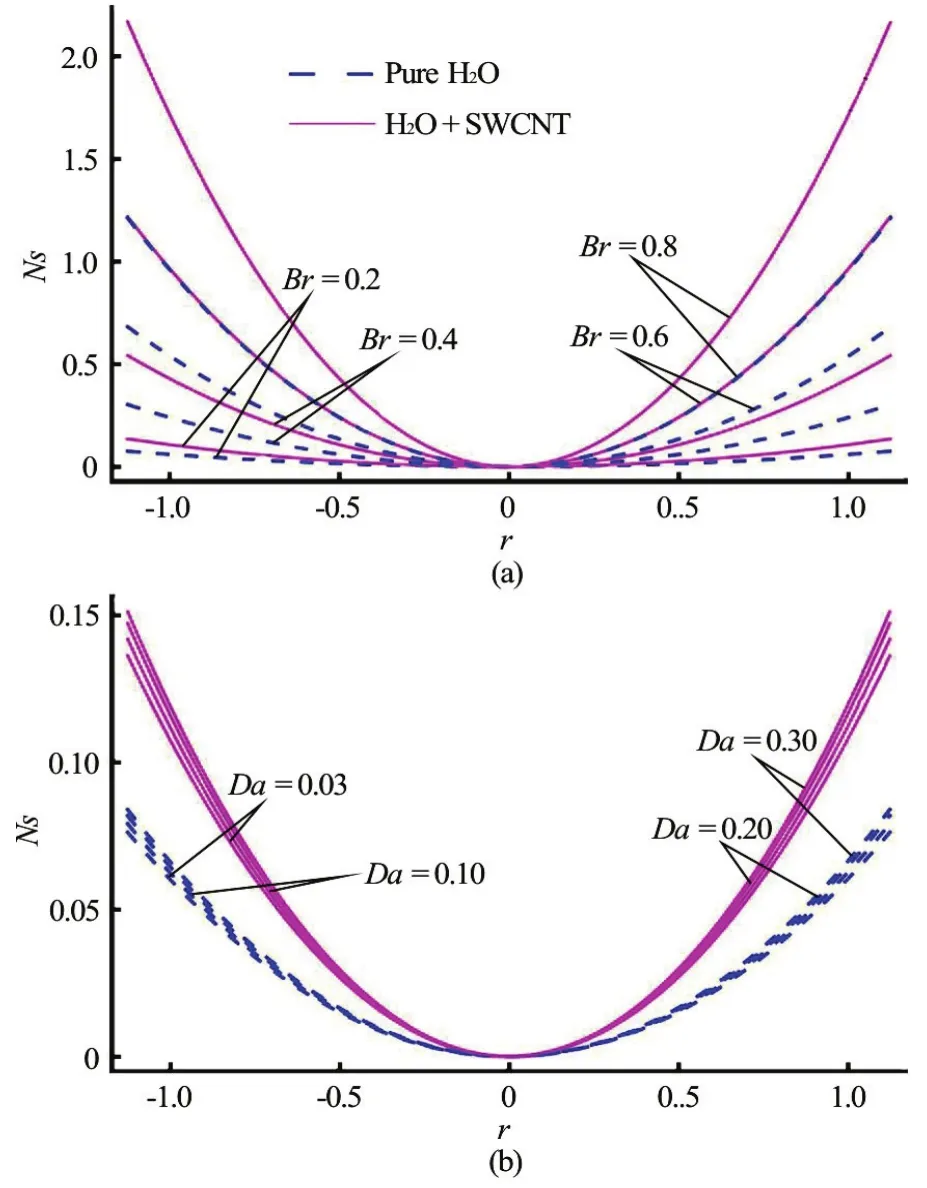
Fig.7 (Color online) Entropy generations against the radial coordinate for different values. Other parameters are fixed i.e., a1 =0.04, ε=0.4, β=0.2, φ=0.3,Q=2.5

pressure gradient is directly proportionalto eccentricity of the elliptical motion ()α whereas it is inversely proportional to flow rate (Q). It is also revealed that the variation in pressure gradient profile with respect to (Q) is greater as compared to ()α.In all cases, the maximum pressure gradient arises at the center of tube length (z=0.5). The flow is therefore strongest in the core region of the tube.Pressure gradient is less for SWCNT-nanofluids in comparison with only the base fluid.

Figures 4(a)-4(c) depict the variation of pressure rise against the flow rate for the effects of slip parameter, Darcy number and eccentricity of the elliptical motion. It is apparent that pressure rise magnitudes for pure water exceed those of SWCNT-nanofluids. Figure 4(a) shows that pressure rise diminishes with increasing magnitude of slip parameter, which is physically logical since flow acceleration occurs with greater slip and this reduces pressure rise.

Figure 4(b) reveals that the pressure increases with increasing value of Darcy number in the pumping region (Δp＞0), whereas the reverse trend is computed in augmented pumping region (Δp＜ 0)and a constant value at free pumping region(Δp=0).

Fig.8 (Color online) Streamlines at a1 =0.04, ε=0.4,β =0.3, φ=0.3, Q=2.0 and various Darcy numbers for pure water

Figures5(a), 5(b) illustrate the effects of Brinkman number and Darcy number on the radial temperature distributions. Brinkman number essentially number essentially embodies the ratio of direct heat conduction from the wall surface to the viscous heat generated by shear in the boundary layer.It is distinct from Eckert number which symbolizes the kinetic energy of flow to the boundary layer enthalpy difference. Brinkman number is in fact more appropriate for low speed, viscous-dominated flows,as considered in the present case, whereas Eckert number often arises in high speed aerodynamic flows.Both parameters are quantifications of viscous dissipation effects. It can be seen that temperature is directly proportional in both cases toBrandDa.Greater Brinkman number implies greater thermal energy conversion from mechanical energy, which inevitably elevates temperatures i.e. heats the regime.With greater Darcy number, permeability is increased which reduces the presence of solid fibers. This reduces thermal conduction heat transfer in the regime but elevates thermal convection heat transfer and the latter results in an elevation of temperatures. Similar results for both Brinkman and Darcy number effects have been reported in many other studies including Baytas[22]and Basak et al.[31]. The rate of temperature change in the case of SWCNT-nanofluids is observed to be very fast in comparison with pure water. The temperature is maximized at the center of the tube and it starts decreasing towards the boundary walls.

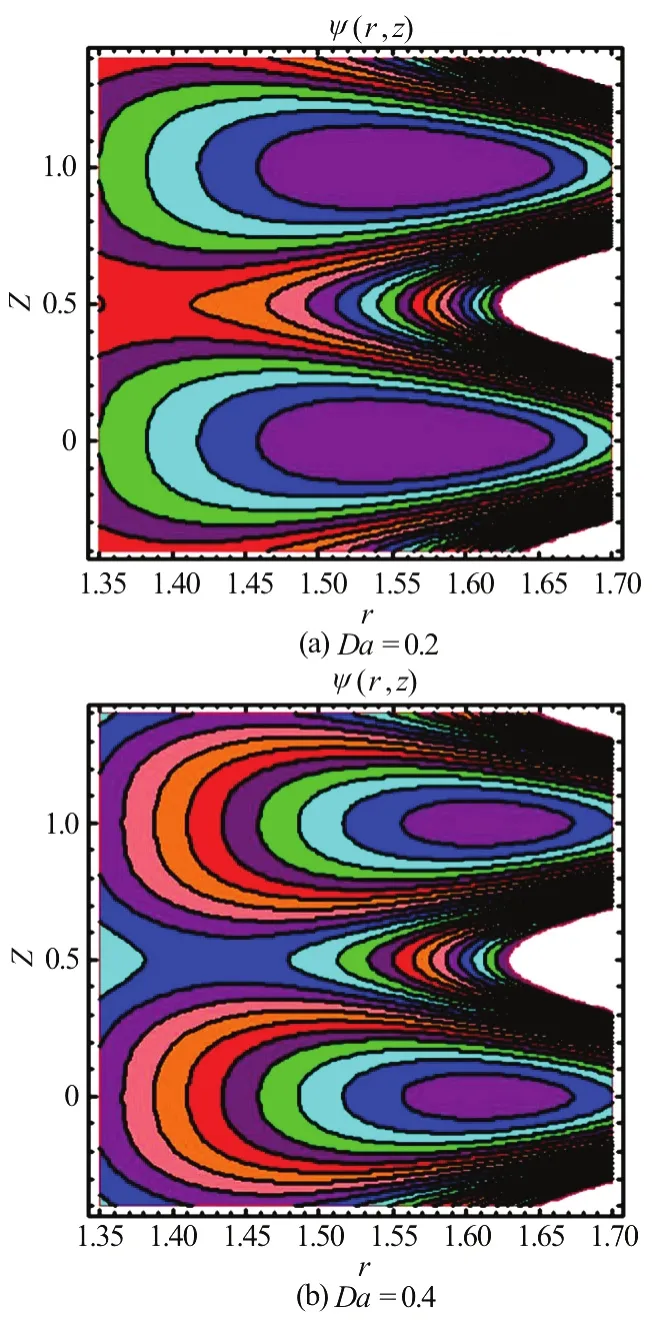
Fig.9 (Color online) Streamlines at a1 =0.04, ε=0.4,β =0.3, φ=0.3, Q=2.0 and various Darcy numbers for SWCNT-nanofluids

Figures 6(a), 6(b) present the variation in Bejan number against the radial coordinate (r) for the influence of Brinkman number and Darcy number. It is found that the profiles are conventional parabolas(unlike the temperature distributions in Figs. 5(a), 5 (b)which are inverted parabolic distributions). It is evident that at zero radial coordinate,Beis a minimum and for positive or negative radial coordinate values, the value of Bejan number increases. It can also be seen thatBeis directly proportional toBrandDa. The changes in Bejan number are greater in SWCNT-nanofluids as compared to pure water.

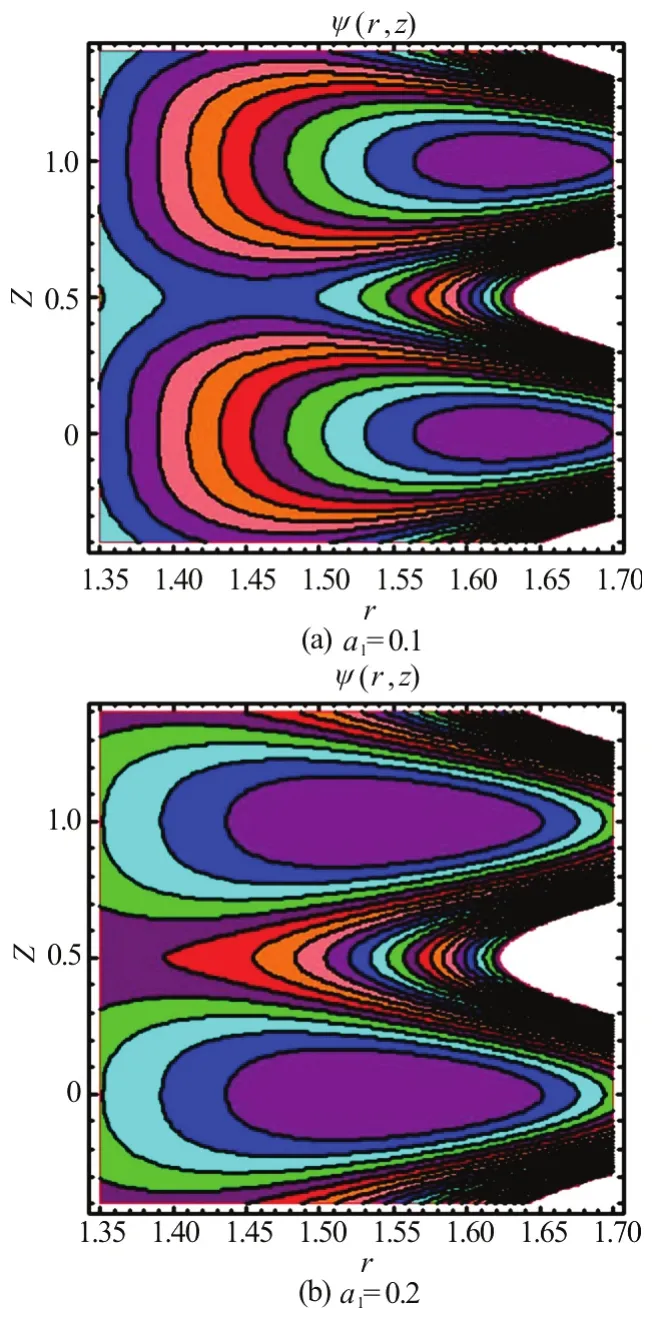
Fig.10 (Color online) Streamlines at Da=0.4, ε=0.4,β= 0.3, φ=0.3, Q=2.0 and various slip parameters for pure water

Figures 7(a), 7(b) present the evolution in entropy generation (Ns) against the radial coordinate are observed with effects of Brinkman number and Darcy number. It is also observed that entropy generation enhances with increasing the magnitude of both parameters i.e., Brinkman number and Darcy number. It is further noted that attains its maximum value at the walls and minimum value at the center of the tube. Another interesting observation is that the change in for the case SWCNT-nanofluids with changes in is slightly different from pure water,however a much greater deviation is observed between SWCNT-nanofluids and pure water with a change in Brinkman number rather than a change in Darcy number.

A very interesting pumping phenomenon, termed trapping is also of relevance in deformable wall flows.This is defined as the process of circulation of stream lines at some particular value of flow rate. The stream lines in the wave frame (obeying the Cauchy-Riemann equations,w=r-1∂ψ /∂randu=-r-1∂ψ /∂z) at ψ= 0are plotted through Figs. 8-11 to study the effects of Darcy number and slip parameter on trapping phenomenon for SWCNT-nanofluids and also base fluid where is dimensional stream function.For pure water the graphs are shown in Figs. 8(a), 8(b)and for SWCNT-nanofluids the graphs are plotted in Figs. 9(a), 9(b) with variation of Darcy number. It is observed that with increment in Darcy number, the trapped bolus inside the streamlines decrease in size in the case of pure water as well as for SWCNT-nanofluids. However when we compare the size of boluses for pure water and SWCNT-nanofluids, the trapped bolus is smaller in size for pure water than that of SWCNT-nanofluids. The presence of SWCNT-nanofluids therefore enhances the bolus magnitude.

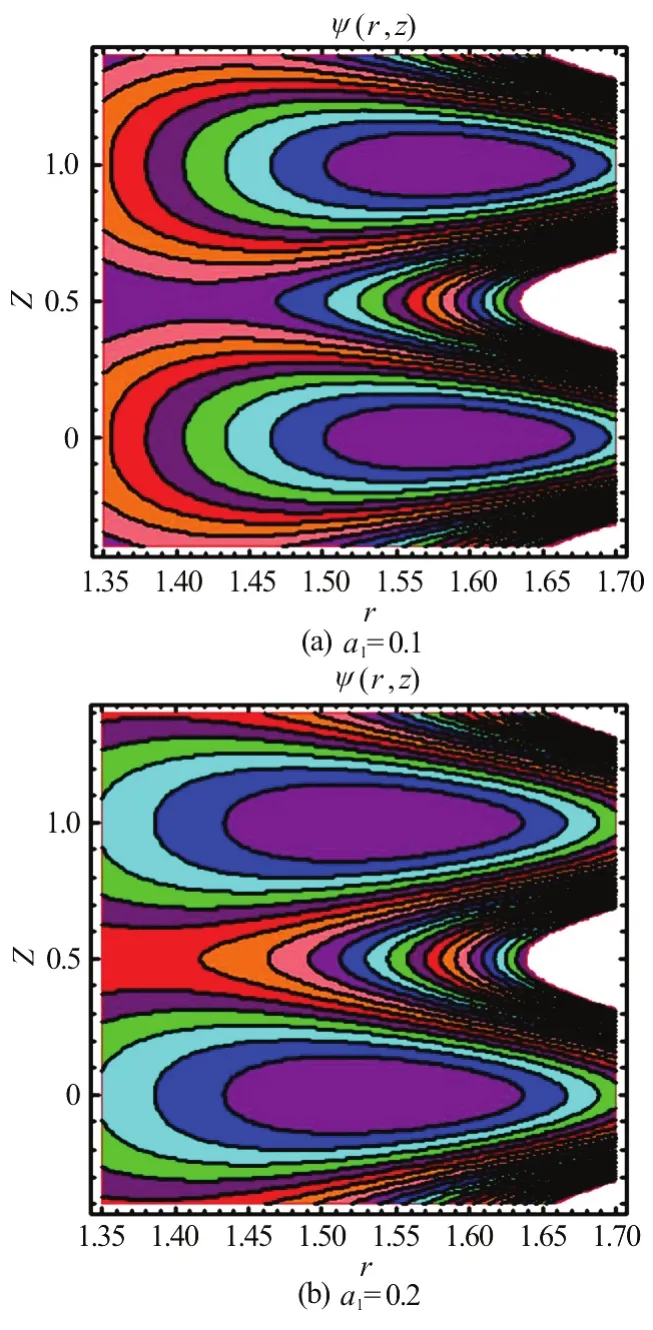
Fig.11 (Color online) Streamlines at Da=0.4, ε=0.4,β =0.3, φ=0.3, Q=2.0 and various slip parameters for SWCNT-Nanofluids

The effects of slip parameter on streamlines for pure water and SWCNT-nanofluids are illustrated in Figs. 10(a), 10(b) and Figs. 11(a), 11(b) for pure water and SWCNT-nanofluids, respectively. Inspection of these figures shows that with increasing value of slip parameter, the trapped bolus inside the streamlines is enhanced in size while the number of bolus reduces in both cases (pure water and SWCNT-nanofluids).

5. Conclusions

A mathematical model has been developed to simulate the effects of pertinent physical parameters on entropy generation and heat transfer of CNT-nanofluid flow driven by metachronal wave generated by beating cilia in a tube containing porous medium with hydrodynamic slip. Based on analytical solutions to the transformed boundary value problem, the present computations have shown that:

(1) Velocity field is enhanced with increasing magnitude of slip parameter and Darcy number(porous medium permeability parameter) and is greater for SWCNT-nanofluids compared with pure water.

(2) Pressure gradient is an increasing function of eccentricity of the cilia elliptical motion whereas it is a decreasing function of flow rate.

(3) Temperature is elevated with increasing magnitude of Brinkman number (viscous dissipation parameter) and Darcy number. Furthermore, the temperature is higher for SWCNT-nanofluids relative to pure water (base fluid).

(4) Entropy generation is enhanced with rising values of both Brinkman number and Darcy number and is greater for SWCNT-nanofluids.

(5) Bejan number follows a parabolic distribution with radial coordinate and is enhanced both with increasing Brinkman number and Darcy number.

(6) Bejan number is of higher magnitude for SWCNT-nanofluids as compared with pure water.

(7) The size of trapped bolus expands with increasing value of slip parameter whereas it contracts with increasing Darcy number.

(8) The size of the trapped bolus for pure water is smaller than that of the SWCNT-nanofluids.

The present simulations have neglected magnetic field effects i.e., electrically-conducting properties of magnetic nanofluids[37,39]which are of some significance in medical engineering applications. These offer an interesting area for future investigations.

Acknowledgements

The authors are grateful to the reviewers for their comments and suggestions which have served to improve the present article.

[1] Xie H., Lee H., Youn W. et al. Nan of luids containing multi walled carbon nanotubes and their enhanced thermal conductivities [J].Journal of Applied Physics,2003, 94(8):4967-4971.

[2] Liu M. S., Lin C. C., Huang I. T. et al. Enhancement of thermal conductivity with carbon nanotube for nanofluids[J].International Communications in Heat and Mass Transfer, 2005, 32(9): 1202-1210.

[3] Ding Y., Alias H., Wen D. et al. Heat transfer of aqueous suspensions of carbon nanotubes (CNT nanofluids) [J].International Journal of Heat and Mass Transfer,2005,32(9): 1202-1210.

[4] Xie H., Chen L. Review on the preparation and thermal performances of carbon nanotube contained nanofluids [J].Journal of Chemical and Engineering Data,2011, 56(4):1030-1041.

[5] Murshed S. S., De Castro C. N. Superior thermal features of carbon nanotubes-based nanofluids–A review [J].Renewable and Sustainable Energy Reviews, 2014, 37(3):155-167.

[6] Halelfadl S., Maré T., Estellé P. Efficiency of carbon nanotubes water based nanofluids as coolants [J].Experimental Thermal and Fluid Science, 2014, 53(2): 104-110.

[7] Said Z., Saidur R., Rahim N. et al. Analyses of exergy efficiency and pumping power for a conventional flat plate solar collector using SWCNTs based nanofluid [J].Energy and Buildings, 2014, 78(4): 1-9.

[8] Hordy N., Rabilloud D., Meunier J. L. et al. High temperature and long-term stability of carbon nanotube nanofluids for direct absorption solar thermal collectors [J].Solar Energy, 2014,105: 82-90.

[9] Yadav D., Bhargava R., Agrawal G. et al. Thermal instability in a rotating porous layer saturated by a non-Newtonian nanofluid with thermal conductivity and viscosity variation [J].Microfluidics and Nanofluidics,2014, 16(1-2): 425-440.

[10] Walvekar R., Siddiqui M. K., Ong S. et al. Application of CNT nanofluids in a turbulent flow heat exchanger [J].Journal of Experimental Nanoscience, 2016, 11(1): 1-17.

[11] Xing M., Yu J., Wang R. Thermo-physical properties of water-based single-walled carbon nanotube nanofluid as advanced coolant [J].Applied Thermal Engineering, 2015,87: 344-351.

[12] Jiang H., Zhang Q., Shi L. Effective thermal conductivity of carbon nanotube-based nanofluid [J].Journal of the Taiwan Institute of Chemical Engineers, 2015,55: 76-81.

[13] Den Toonder J. M., Onck P. R. Microfluidic manipulation with artificial/bioinspired cilia [J].Trends in biotechnology, 2013, 31(2): 85-91.

[14] Blake J. A model for the micro-structure in ciliated organisms [J].Journal of Fluid Mechanics, 1972,55:1-23.

[15] Khaderi S., Onck P. Fluid–structure interaction of three dimensional magnetic artificial cilia [J].Journal of Fluid Mechanics,2012,708: 303-328.

[16] Khaderi S., Baltussen M., Anderson P. et al. Breaking of symmetry in microfluidic propulsion driven by artificial cilia[J].Physical Review E, 2010, 82(2): 027302.

[17] Khaderi S., Den Toonder J., Onck P. Microfluidic propulsion by the metachronal beating of magnetic artificial cilia:A numerical analysis [J].Journal of Fluid Mechanics,2011,688: 44-65.

[18] Bejan A. A study of entropy generation in fundamental convective heat transfer [J].Journal of Heat Transfer,1979, 101(4): 718-725.

[19] Bejan A. The concept of irreversibility in heat exchanger design: Counterflow heat exchangers for gas-to-gas applications [J].Journal of Heat Transfer, 1977, 99(3):374-380.

[20] Bejan A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes [J].Journal of Applied Physics, 1996, 79(3):1191-1218.

[21] Abu-Qudais M., Nada E. A. Numerical prediction of entropy generation due to natural convection from a horizontal cylinder [J].Energy, 1999, 24(4): 327-333.

[22] Baytaş A. Entropy generation for natural convection in an inclined porous cavity [J].International Journal of Heat and Mass Transfer, 2000, 43(12): 2089-2099.

[23] Makinde O. D., Bég O. A. On inherent irreversibility in a reactive hydromagnetic channel flow [J].Journal of Thermal Science, 2010, 19(1): 72-79.

[24] Rashidi M., Bég O. A., Parsa A. B. et al. Analysis and optimization of a transcritical power cycle with regenerator using artificial neural networks and genetic algorithms [J].Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2011,225(6): 701-717.

[25] Rashidi M., Bég O. A., Habibzadeh A. First and second law analysis of an ejector expansion Joule–Thomson cryogenic refrigeration cycle [J].International Journal of Energy Research, 2012, 36(2): 231-240.

[26] Bég O. A., Mehr N. F., Rostami B. Second law analysis of hydromagnetic flow from a stretching rotating disk:DTM-Padé simulation of novel nuclear MHD propulsion systems [J].Frontiers in Aerospace Engineering, 2013,2(1): 29-38.

[27] Rashidi M., Parsa A. B., Bég O. A. et al. Parametric analysis of entropy generation in magneto-hemodynamic flow in a semi-porous channel with OHAM and DTM [J].Applied Bionics and Biomechanics, 2014, 11(1-2): 47-60.

[28] Öztop H. F., Şahin A. Z., Dağtekin İ. Entropy generation through hexagonal cross-sectional duct for constant wall temperature in laminar flow [J].International Journal of Energy Research, 2004, 28(8): 725-737.

[29] Dağtekin İ., Öztop H. F., Şahin A. Z. An analysis of entropy generation through a circular duct with different shaped longitudinal fins for laminar flow [J].International Journal of Heat and Mass Transfer, 2005, 48(1): 171-181.

[30] Dağtekin İ., Öztop H. F., Bahloul A. Entropy generation for natural convection in Γ-shaped enclosures [J].International Communications in Heat and Mass Transfer,2007, 34(4): 502-510.

[31] Basak T., Anandalakshmi R., Kumar P. et al. Entropy generation vs energy flow due to natural convection in a trapezoidal cavity with isothermal and non-isothermal hot bottom wall [J].Energy, 2012,37: 514-532.

[32] Guelpa E., Sciacovelli A., Verda V. Entropy generation analysis for the design improvement of a latent heat storage system [J].Energy, 2013,53: 128-138.

[33] Anand V. Slip law effects on heat transfer and entropy generation of pressure driven flow of a power law fluid in a microchannel under uniform heat flux boundary condition [J].Energy, 2014,76: 716-732.

[34] Akbar N. S. Entropy generation and energy conversion rate for the peristaltic flow in a tube with magnetic field[J].Energy, 2015,82: 23-30.

[35] Ellahi R., Hassan M., Zeeshan A. Shape effects of nanosize particles in Cu–H2O nanofluid on entropy generation[J].International Journal of Heat and Mass Transfer,2015,81: 449-456.

[36] Ellahi R., Rahman S., Nadeem S. Blood flow of Jeffrey fluid in a catherized tapered artery with the suspension of nanoparticles [J].Physics Letters A, 2014, 378(40):2973-2980.

[37] Akbar N. S., Raza M., Ellahi R. Influence of induced magnetic field and heat flux with the suspension of carbon nanotubes for the peristaltic flow in a permeable channel[J].Journal of Magnetism and Magnetic Materials, 2015,381: 405-415.

[38] Ellahi R., Rahman S., Nadeem S. et al. Blood flow of nanofluid through an artery with composite stenosis and permeable walls [J].Applied Nanoscience, 2014, 4(8):919-926.

[39] Sheikholeslami M., Bandpy M. G., Ellahi R. et al. Effects of MHD on Cu-water nanofluid flow and heat transfer by means of CVFEM [J].Journal of Magnetism and Magnetic Materials, 2014,349: 188-200.

[40] Nadeem S., Sadaf H. Theoretical analysis of Cu-blood nanofluid for metachronal wave of cilia motion in a curved channel [J].IEEE Transactions on Nanobioscience,2015, 14(4): 447-454.