基于系数运算的并行CRC算法

张笑铭，梁利平，王志君

（1.中国科学院大学北京100029；2.中国科学院微电子研究所，北京100029）

CRC（循环冗余校验）是通信领域广泛使用的一种校验算法，它将计算出的校验码添加在数据位之后，为通信过程提供校验能力。CRC分为串行CRC和并行CRC[1]，串行CRC每个周期只能输入一位数据进行计算，通常使用LFSR[2-3]（线性反馈移位寄存器）进行实现。并行CRC每个周期可以同时输入多位数据，用并行度这一参数来表示它每个周期计算的数据位数。相比串行CRC，并行CRC效率更高，但相应的算法复杂度也较大。一种普遍的做法是查表法[4]，事先将数据的CRC校验码存储在一张表中，使用时直接查表就可以得到要计算的CRC校验码，但缺点是表不能太大，一般按字节进行计算，即并行度为8，此时表的大小为2的8次方。如果需要同时输入4字节进行计算，那么表的大小为2的32次方，这时表所占用的存储空间太大，难以实现。由于查表法适用于较小并行度下使用，因此限制了数据传输的速度。文献[5-7]提出同时计算多次串行CRC完成并行CRC的计算，该方法虽然不需要额外的存储资源，但在并行度较大时推导复杂，并且并行度改变时又需要重新计算。矩阵法[8-10]可以满足并行度较大的情况，但由于涉及大量的矩阵乘法运算，复杂度较高。文献[11-12]提前将矩阵乘法的结果计算出来，但由于不同并行度的矩阵乘法结果不同，需要在计算之前固定好并行度，在需要多种并行度计算的情况下就要为每种并行度计算矩阵乘法的结果，并且只适合于并行度小于生成多项式位数的情况。文献[13-16]提出针对多并行度CRC计算的解决方法，但其资源占用过多且延时较大。本文中的算法利用并行CRC中特殊矩阵的性质，将矩阵乘法的计算简化成矩阵列向量之间的线性组合，只需要计算出该线性组合的系数，可以同时完成多种并行度的CRC计算。在软件层面，该算法在并行度较小时，运行时间大于矩阵法，随着并行度增大，运行时间逐渐小于矩阵法并趋于固定值。在硬件层面，该算法与矩阵法相比在占用更少资源的情况下可以获得更高的工作频率。

1 并行CRC算法

CRC算法的原理是假设发送一个k位的序列，将其表示为{d0，d1，…，dk-1}，为了验证其发送和传输过程中是否发生错误，需要在数据位之后添加校验位，校验位的生成需要一个（m+1）位的生成多项式，省略掉最高位系数（最高位系数恒为1），表示为{pm-1，pm-2，…po}。生成方法是将原本的信息位左移m位后除以生成多项式，这里的除法是二进制除，最终得到的余数就是所要添加的CRC校验码。检测过程将接收到的结果除以生成多项式，如果能被整除，说明数据正确，否则发生了错误。

并行CRC算法每次可以同时输入多位数据进行计算，当所有的数据位输入完成后产生最终的校验位，而串行CRC算法每次只能输入一位数据，所以速度上要比并行CRC算法慢。但串行CRC算法的优点是实现简单并且耗费资源少，适用于对速度要求不高的场合，而对数据处理速度有较高要求时，就需要使用在串行CRC算法基础上推导出的并行CRC算法。

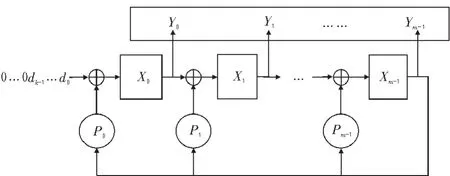
图1 串行CRC实现

由于串行CRC算法一般采用LFSR实现（如图1），而LFSR可以看作是一个离散的线性时不变系统[1]，由线性系统的理论，一个离线的线性时不变系统可以使用方程组来表示。

其中，X表示系统的状态，Y表示系统的输出，U表示系统的输入。X，Y，U为列向量，F，G，H，J为矩阵。通过对此系统进行分析并结合LFSR的性质，可以得出在这个系统中系统的状态同时是系统的输出，即Y=X。因此由第二个方程可以推出H为单位矩阵，J为零矩阵。而第一个方程可以推出

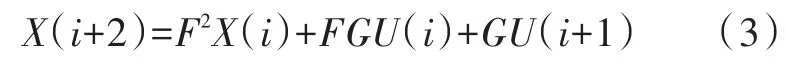
依次类推可以得到一个公式，这个公式就是并行CRC算法的基本公式。

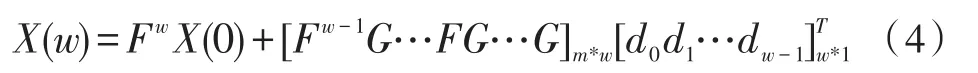
对上面式子使用Galois Field理论，将式中的加法用按位异或运算代替，乘法使用按位与来代替，式子仍然成立。式子变为

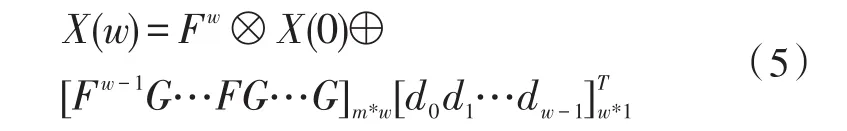
式（5）就是矩阵法所用的公式，w为并行度参数。为了求出w位输入后的系统状态（也就是CRC校验的输出），需要求解F矩阵的1到w次方，因此涉及到大量的矩阵乘法运算。

2 基于系数运算的并行CRC算法

基于系数运算的并行CRC算法在并行CRC公式的基础上推导而来，由文献[1]中并行CRC的生成特性可知X=[xm-1…x1xo]T，G=[0 0 … 0 1]，F=

将一个矩阵表示为列向量的形式T=[t0t1…tm-1]，根据矩阵乘法的性质，其与F矩阵相乘的结果是T·F=[pm-1·t0+…+p0·tm-1t0t1…tm-2]，可以看出是此矩阵每列向右移动一位，第一列变成F第一列每个元素与此矩阵每一列做与运算然后求和的结果。将F矩阵也表示为列向量的形式F=[f0f1…fm-1]，这样F矩阵平方的列向量可以表示为F列向量线性组合的形式。

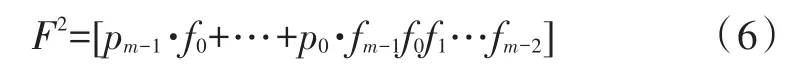
F矩阵n次方的列向量也是F列向量线性组合的形式，区别只是每个列向量的系数不同。当其与某个列向量相乘时，结果是一个列向量，这个列向量也是F列向量的线性组合。

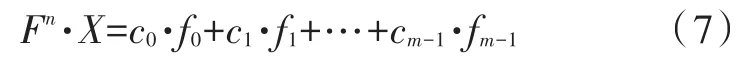
F的（w-1）次方到1次方与列向量G相乘都可以表示为F列向量的一个线性组合，仅仅是列向量的系数不同，所以关键问题就是求出F每一列向量的系数。因为列向量G也可以看作是F的列向量的线性组合。

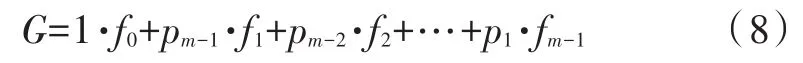
所以列向量G的系数为[1pm-1pm-2…p1]，为了求得FG的系数，对其进行化简。

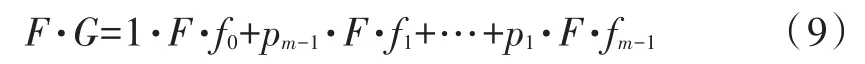
将F展开为列向量[f0f1…fm-1]，原本相乘的列向量按元素展开并进行整理合并。

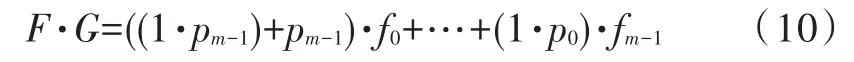
因此FG系数为[((1·pm-1)+pm-1)+((1·pm-2)+pm-2)…(1·p0)]，把系数用新的符号表示。

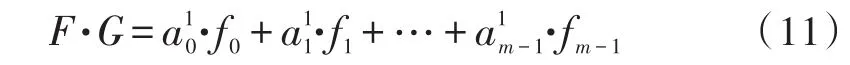
同样为求得F的2次方与G乘积的系数，也需要对其进行整理化简。

F的2次方与G乘积的系数为，依次类推就可以得到F各次方与列向量G相乘的系数表示。

F的w次方每列的系数表示也适用上述类推规则，这是因为G=[0 0 … 0 1]T，Fw·G的结果就是Fw的最后一列，Fw+1·G的结果是Fw的倒数第二列（Fw与F相乘是Fw每列向右移动一位），依次进行下去直到最后Fw+m+1是Fw的第一列，因此可以从系数开始（初值为 [1pm-1pm-2…p1]），按照来生成下一系数表示，直到生成（w+m）次，这样就得到了Fw列向量和[Fw-1G…FG…G]的系数表示。

由于每个系数表示都可以看作是行向量，因此可以把这些行向量组合成一个系数矩阵

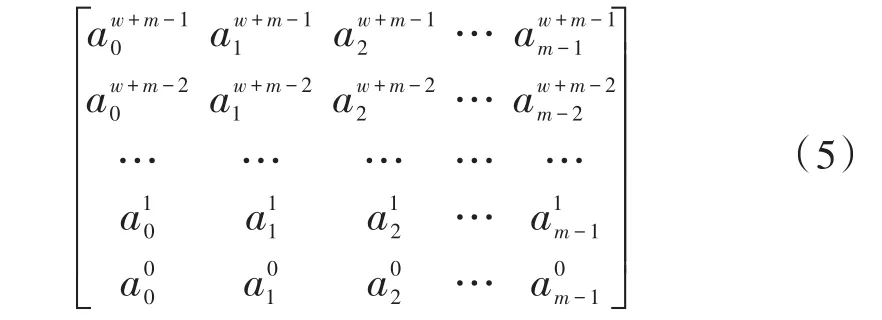
根据矩阵法的公式（式（5）），将系统当前状态与输入数据组成列向量[xm-1…x1x0d0d1…dw-1]T，此列向量分别与系数矩阵的每一列按位与，得到的结果向量中元素之和（用异或代替）就是一个系数的最终计算结果。因此将每个结果向量进行缩减异或运算，得到最终的系数向量[a0a1a2…am-1]，把系数代入线性组合表达式中，就可以获得w位数据输入后系统的状态，同时也是系统的输出。

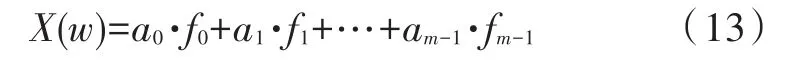
基于系数运算的并行CRC算法可以同时实现多种并行度的CRC计算，当并行度变为w1时（w1小于w），根据矩阵法的公式，需要求出Fw1和[Fw1-1G…FG…G]，因为其系数矩阵和并行度为w时的系数矩阵最后（w1+m）行相同，所以可以将系统当前状态与输入的w1位数据组成列向量，然后在此列向量的起始补 0到（w+m）维，列向量变为[0…0xm-1…x1x0d0d1…dw1-1]T，此时按照并行度为w的方法计算就可以得到并行度为w1时的CRC校验码。

图2 基于系数运算的并行CRC实现

算法的多数操作都是位运算，消除了矩阵法当中大量的乘法运算，因此易于硬件电路的实现，其电路结构如图2所示，可以看出硬件电路的结构和算法实现步骤一致。

3 实验结果

在MATLAB上比较矩阵法和基于系数运算的并行CRC算法的运行时间，设定生成多项式为CRC-32的生成多项式，并行度分别为1，2，4，8，16，32，64和128，测试数据共1 000组，每组大小128字节。实验主机配置：CPU型号Intel Core i5，主频2.7 GHz，内存8 GB。统计在不同并行度下一组数据的平均运行时间，绘制矩阵法和系数运算法的平均运行时间随并行度变化曲线（如图3）。

基于系数运算的并行CRC算法随着并行度的增加运行时间首先递减然后逐渐趋于固定值。因为随着并行度逐渐增大，计算的次数变少，相应的运行时间也在变少，虽然生成系数矩阵的时间随着并行度的增大而增加，但增加的时间小于减少的时间，运行时间出现下降的趋势。当并行度增加到一定程度后，增加的时间和减少的时间基本一致，因而逐渐平稳。矩阵法的运行时间先递减然后线性递增。因为当并行度较小时，计算矩阵的w次方与计算次数相比对运行时间影响较小，因此随着并行度增大运行时间逐渐减少。当并行度w继续增大时，计算矩阵的w次方所用的时间迅速增加，由于较大并行度下的计算次数变化不明显，因而运行时间又开始逐渐递增。根据实验结果，当并行度大于14时，基于系数运算的并行CRC算法运行时间开始小于矩阵法。

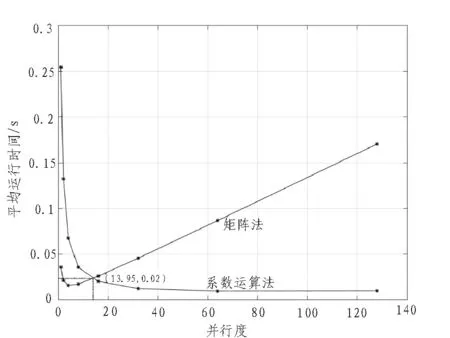
图3 矩阵法和系数运算法运行时间变化曲线

在Xilinx型号为XC6VSX475T的FPGA上进行算法的硬件实现，将其并行度分别设为32，64和128，综合以及布局布线后查看其资源使用率和最高工作频率，与矩阵法的对比如表1，表2和表3所示。

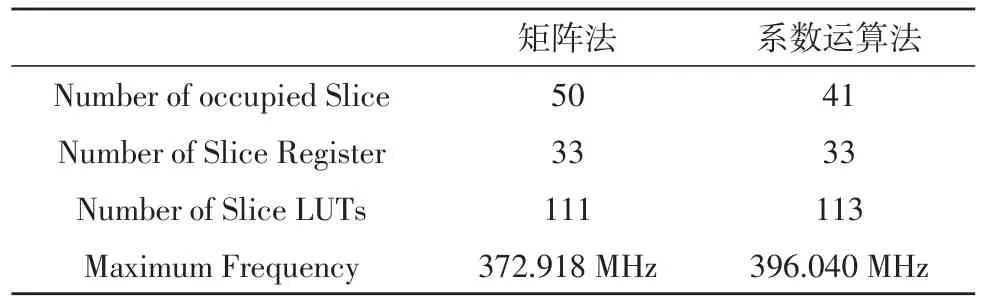
表1 并行度32综合布线结果对比

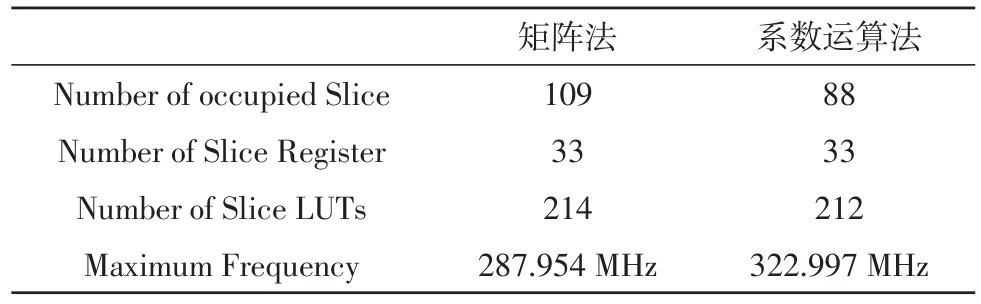
表2 并行度64综合布线结果对比

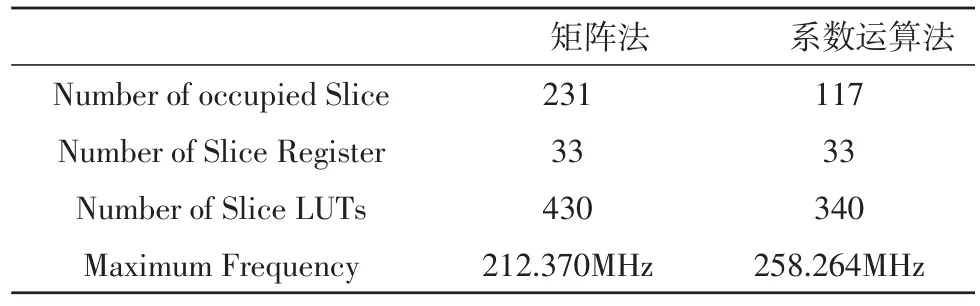
表3 并行度128综合布线结果对比

在并行度为32时，`系数运算法比矩阵法占用的资源少18%，工作频率比矩阵法高6%。在并行度为64时，系数运算法比矩阵法占用的资源少19%，工作频率比矩阵法高12%。在并行度为128时，系数运算法比矩阵法占用的资源少49%，工作频率比矩阵法高21%。并行度越大系数运算法优势越明显，因此更适合于对并行度有较高要求的情况下使用。

4 结论

在并行CRC公式基础之上利用特殊矩阵性质推导出基于系数运算的并行CRC算法。此算法相比矩阵法减少了计算量，并且和矩阵法一样具有通用性，适合于任意并行度的CRC计算。未来的工作是探索其在以太网等对速度要求很高且需要多种并行度情况下的具体应用。

参考文献：

[1]Campobello G，Patane G，Russo M.Parallel CRC realization [J].IEEETransactions on Computers，2003，52（10）:1312-1319.

[2]李永基，魏文军.基于LFSR的CRC校验码在FPGA上的实现[J].兰州交通大学学报，2015，34（6）:91-94.

[3]郑诚玮，戴紫彬，李伟.面向可重构并行化处理的线性反馈移位寄存器统一架构研究[J].微电子学与计算机，2015，32（11）:111-115.

[4]季鹏辉，孟丁，任勇峰.基于FPGA的16bit CRC校验查表法设计[J].电子器件，2013，36（4）:580-584.

[5]朱荣华.一种CRC并行计算原理及实现方法[J].电子学报，1999，27（4）:143-145.

[6]阚佳冲，潘文明，郑坚泽，等.基于FPGA全参数化CRC的推导及实现[J].现代电子技术，2015，38（8）:154-158.

[7]刘伟，王俊芳，王立莹，等.千兆以太网MAC中CRC算法的设计与实现[J].通信技术，2012，45（7）:36-38.

[8]刘昭，苏厉，金德鹏，等.10G以太网系统中的并行CRC编解码器的设计[J].电子技术应用，2004，30（4）:47-50.

[9]梁海华，盘丽娜，赵秀兰，等.CRC查询表及其并行矩阵生成方法[J].计算机科学，2012，39（6）:154-158.

[10]梁海华，盘丽娜.快速CRC逆序校验方法[J].计算机应用，2013，33（7）:1833-1835.

[11]陈玉泉.一种并行CRC算法的实现方法[J].现代电子技术，2005，28（22）:21-23.

[12]薛俊，段发阶，蒋佳佳，等.基于Matlab的并行循环冗余校验Verilog代码自动生成方法[J].计算机应用，2016，36（9）:2503-2507.

[13]袁征，冶晓隆，郭超.基于FPGA的10G以太网并行CRC设计[J].计算机工程与设计，2014，35（5）:1510-1515.

[14]B Li，ZP Huang，SJ Su，et al.Implementation of CRC in 10-Gigabit Ethernet Based on FPGA[J].Applied Mechanics&Materials，2014，599-601:1548-1552.

[15]钟桂森，易清明，石敏.一种新型的10G以太网并行循环冗余校验设计[J].计算机工程，2016，42（5）:292-296.

[16]张友亮，刘志军，马成海，等.万兆以太网MAC层控制器的FPGA设计与实现[J].计算机工程与应用，2012，48（6）:77-79.