超高速空气电主轴动态特性的有限元分析*

，，，，

(1.西华大学 机械工程学院，四川 成都 610039；2.仪陇县交通运输局，四川 南充 637000)

1 超高速空气电主轴应用及结构

随着消费电子产品需求量的快速增加，PCB电路板的需求量也呈快速增长的趋势。为了满足板中微细孔(Φ0.05～Φ0.2 mm)的高精度、高效率的加工要求，超高速空气电主轴被广泛应用于加工行业。以压缩空气为润滑剂的静压轴承由于无固体接触，具有精度高、极限转速高、寿命长、振动小等特点，非常适合作为超高速电主轴的支承元件。但是由于空气的可压缩性、低粘度等固有特性，超高速空气电主轴的承载能力和刚度较小，且在高速运行过程中，电主轴容易出现不稳定现象，严重影响超高速空气电主轴的加工性能，限制了超高速空气电主轴技术的应用与发展[1-2]。

目前国内生产的超高速空气电主轴能够达到的转速是80000～100000 rad/min，主轴回转精度1 μm。本文以广东某电主轴制造公司WF80-01型空气电主轴为研究对象，利用大型有限元分析软件ANSYS，对超高速电主轴系统的动态特性及稳定性进行分析，其结构如图1。

1-后盖；2-气缸外壳；3-气缸座；4-止推；5-后轴承；6-本体外壳；7-本体；8-顶杆；9-三相异步电机定子；10-前轴承；11-气嘴0-3；12-蝶形弹簧；13-主轴夹头；14-轴芯；15-鼠笼转子。

2 空气电主轴有限元模型及分析

WF80-01空气电主轴的结构特点是前轴承采用空气静压轴承，后轴承采用角接触轴承，电机采用三相异步鼠笼电机，转子镶嵌于两轴承之间的主轴中。由于轴承与主轴之间的结合面模型对动态特性影响较大，因此建立合理的结合面模型对空气电主轴有限元分析结果的影响至关重要[3-4]。本文将空气电主轴简化为中空的阶梯轴，把电机转子纳入为主轴结构的一部分，分配同一单元；轴承简化为弹性支撑，前轴承(空气轴承)气膜区采用微小单元法对气膜刚度进行计算。简化后的三维模型如图2。

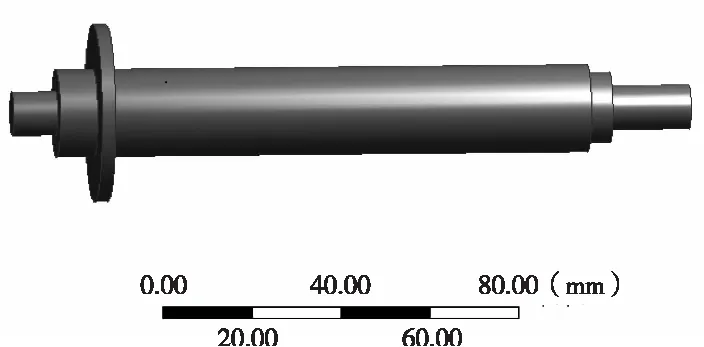
图2 主轴模型示意图

模态分析是动力学分析的基础，其分析的目的是得到空气电主轴系统的固有频率及相应的振型，而且模态分析也是谐响应分析的基础。它主要由四个步骤组成：建模、划分网格及边界条件设置、加载及求解、结果后处理。本文通过三维建模软件UG进行建模，然后导入ANSYS中，进行空气电主轴的有限元动态分析。采用子空间法进行模态提取，供气压力为0.5 MPa，气膜刚度为12 N/μm[5]。网格尺寸大小为2 mm，网格的划分方法设置为自动网格划分，其划分效果图如图3。

图3 主轴网格划分示意图

结合电主轴的实际运作情况，此处设定模拟主轴的六阶模态，根据电主轴的实际工作情况，取其前四阶振型，其具体模态振型图如图4、图5、图6。

由于主轴在旋转方向上的自由度没有约束，故一阶的固有频率为0 Hz，其振动类型为刚性振动，可以忽略不计。

图4 二阶主轴变形位移图

图5 三阶主轴变形位移图

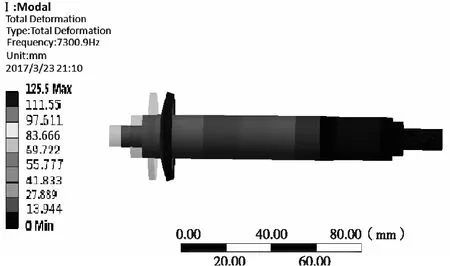
图6 四阶主轴变形位移图

从上述图4、5、6中的振动模态图可以得出电主轴系统在前4阶的振动频率和主轴的变形类型如表1。

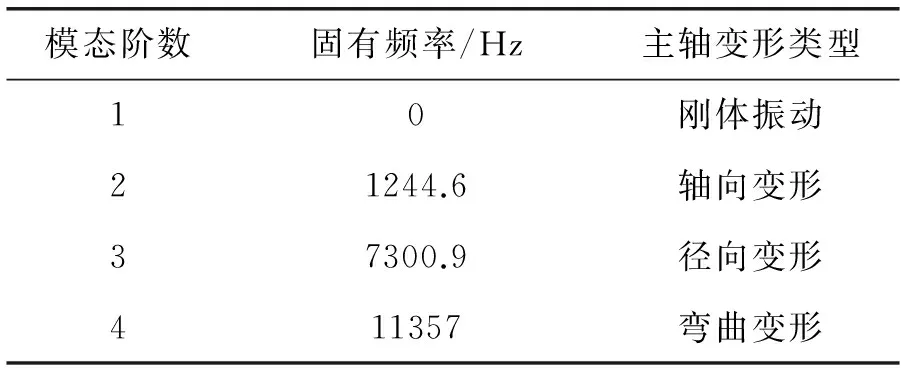
表1 主轴前四阶固有频率和变形类型

3 空气电主轴的临界转速的计算

对于处于工作运转状态下的电主轴首要问题就是共振现象，当电主轴的运转频率与其本身的固有频率接近时就会发生共振现象。此时主轴就会发生剧烈的振动，主轴前面的轴端位移就会变大，严重破坏电主轴系统的动态稳定性。这不仅不利于电主轴高精度的加工而且可能会使主轴发生“抱轴”现象损毁主轴。所以，临界转速的大小很重要。虽然不同的频率对应不同的临界转速，但是，由于其模态振型主要受低阶的影响，因此这里只对前四阶的频率对应的临界转速进行研究即可[6]。

依据上面的模态分析的频率此处可求得各阶不同的临界转速。由公式可知，临界转速和固有频率的运算关系为[7]：

n=60f

(1)

其中：n主轴的临界转速(r/min)；f主轴的固有频率(Hz)。根据此方程式可得到其各阶的临界转速如表2。

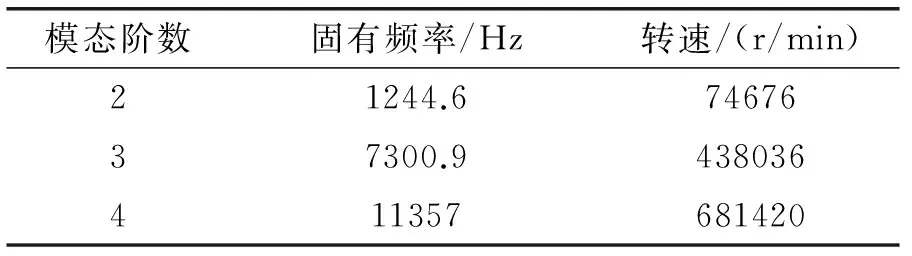
表2 固有频率和临界转速

由表2可以看出，主轴系统的二阶临界转速是74676 r/min，而本文电主轴的最高转速为100000 r/min，明显低于其临界转速。

4 空气主轴系统的谐响应分析

对超高速空气电主轴的谐响应分析，主要是针对模态分析得出的前四阶固有频率进行分析，围绕固有频率选取不同频率的载荷激励，通过ANSYS分析软件得出的频率和振幅二者之间的关系图进行分析，其中振幅的大小与外界激励载荷的大小有很大的关系[8]。对于超高速机床来说，电主轴的轴端往往会安装刀具来进行加工工作，刀具受到周期切削力的作用就会传递给主轴使其产生动态响应，存在着或大或小的变形位移。当切削力的作用频率接近主轴的固有频率时产生共振现象，严重影响电主轴系统的加工精度、稳定性和质量，严重时还会造成电主轴结构的破坏，因此要求主轴转速应该尽量避免出现在固有频率的附近。分析主轴的谐响应情况，可以得出其对于外界激励作用下响应的情况，为电主轴实际运行提供依据[9]。

谐响应分析是在已完成的模态分析的基础上，运用完成分析方法，对主轴的谐响应情况进行分析。谐响应分析的过程和模态分析相似，唯一不同就是要额外给主轴添加一个具有一定规律的外载荷力。为了分析的统一性，这里统一给主轴施加一个大小为5 N的外载荷激励力，作用点是主轴的前端面，分别分析二阶、三阶、四阶固有频率处主轴前端面的位移。而载荷力的方向就要根据各阶的主要变形来确定[10]。

4.1 二阶主轴频率响应分析

由图4，可以看出高速电主轴在二阶f=1244.6 Hz时，主轴主要位移变形是轴向变形，因此所添加的外载荷力激励的方向应与主轴的主要变形相同即轴向方向，而频率范围则以1244.6 Hz为关键点取一个合适的范围，即频率的取值范围为1000 Hz～1400 Hz。在上述的条件下分析得到电主轴前端面的位移—频率关系图(图7)。通过图7可以看出主轴在频率1200 Hz～1280 Hz范围内，其位移响应比较敏感。其中当频率为1200 Hz～1244.6 Hz时，主轴前端的位移响应随着频率的增大而快速增大，此时电主轴的刚度则迅速降低，而当频率为1244.6 Hz～1280 Hz时，主轴前端的位移响应随着频率的增大而快速减少，此时电主轴的刚度迅速增大[11]。其它频率范围主轴的位移响应缓慢，刚度区域较稳定，因此，在这个频率范围内有利于电主轴的持续工作。当频率f=1244.6 Hz时，主轴前端轴向位移的响应值最大[12]。

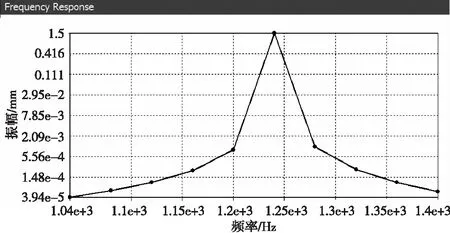
图7 二阶频率响应图

4.2 三阶主轴频率响应分析

由图5可看出超高速电主轴在三阶f=7300.9 Hz时，主轴的主要位移变形是径向变形，因此此处所添加的外载荷力激励的方向应与主轴的主要变形相同即径向方向，而频率范围则以7300.9 Hz为关键点取一个合适的范围即频率范围取6500 Hz～7500 Hz。在上述的条件下分析得到电主轴前端面的位移—频率关系图(图8)。通过图8可以看出主轴在频率7200 Hz～7400 Hz范围内，其位移响应比较敏感。其中当频率为7200 Hz～7300.9 Hz时，主轴前端的位移响应随着频率的增大而快速增大，其电主轴的刚度也迅速降低，而当频率为7300.9 Hz～7400 Hz时，主轴前端的位移响应随着频率的增大而快速减少，则说明其电主轴的刚度迅速增大。在其它频率范围内，主轴的位移响应缓慢，刚度区域较稳定，因此，在这个频率范围有利于电主轴的持续工作。主轴在激励频率f=7300.9 Hz时，前端径向位移响应值最大[13-14]。

图8 三阶频率响应图

4.3 四阶主轴频率响应分析

由2节图6可以看出超高速电主轴在四阶f=11357 Hz时，主轴的主要位移变形是弯曲变形，而针对为了分析主轴的径向位移，因此此处所添加的外载荷力激励的方向为径向方向，而频率范围则以11357 Hz为关键点取一个合适的范围，即频率范围取11000 Hz～11500 Hz。在上述的条件下分析得到电主轴前端面的位移—频率关系图(图9)。通过图9可以看出主轴在频率11300 Hz～11400 Hz范围内，其位移响应比较敏感。其中当频率为11300 Hz～11357 Hz时，主轴前端的位移响应随着频率的增大而快速增大，故其电主轴的刚度也迅速降低，而当频率为11357 Hz～11400 Hz时，主轴前端的位移响应随着频率的增大而快速减少，则说明其电主轴的刚度迅速增大。其它频率范围内，主轴的位移响应缓慢，刚度区域较稳定，因此，在这个频率范围内有利于电主轴的持续工作。当频率f=11357 Hz时，主轴前端径向位移的响应值最大[15]。

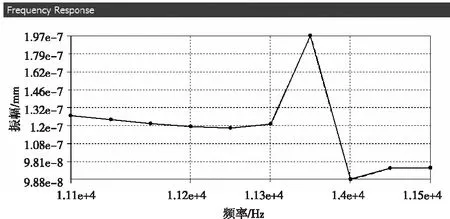
图9 四阶频率响应图

5 结束语

空气静压电主轴是超高机床的核心部件，其动态特性对机床的加工质量有显著影响，本文主要围绕空气静压电主轴的动态特性展开分析，最后结果表明：WF80-01型空气静压电主轴在轴承弹性支撑情况下的各阶固有频率与振型之间关系，通过各阶振型图可以看出电主轴的扭转弯曲分布情况，然后计算出了电主轴的临界转速及其对应的频率。此外，通过上述谐响应分析可知，空气电主轴当外载荷激励的频率在f=1244.6 Hz、f=7300.9 Hz以及f=11357 Hz时，发生共振现象。主轴前端面的振动位移相比于其它的频率范围会发生明显的增大。因此，本文设计的高速电主轴要避开上面的三处频率，消除共振现象的发生，为高速电主轴运行提供相关的理论依据。

[1] 李松生，陈晓阳，张钢，等.超高速时电主轴轴承的动态支承刚度分析[J].机械工程学报，2006，42(11)：60-65.

[2] 曹宇，李强.高速电主轴动态特性的有限元分析[J].包钢科技，2013，39(3)：53-55.

[3] HARRIS T A.Rolling Bearing Analysis[M].Wiley，1984.

[4] YANG D W，CHEN C H，KANG Y，et al.Influence of orifices on stability of rotor-aerostatic bearing system[J].Tribology International，2009，42(8)：1206-1219.

[5] YANG P，ZHU KQ，WANG XL.On the non-linear stability of self-acting gas journal bearings[J].Tribology International，2009，42(1)：71-76.

[6] TOBIAS S A.Machine-tool vibration[M].Blackie，1965.

[7] 王晓明，袁艳.电主轴动态特性分析及结构优化[J].现代制造工程，2013，(8)：53-55.

[8] 熊万里，侯志泉，吕浪，等.气体悬浮电主轴动态特性研究进展[J].机械工程学报，2011，47(5)：40-58.

[9] 王冰，胡志超，汤宏群.PCB钻床超高速电主轴特点及关键技术分析[J].机床与液压，2011，39(17)：42-47.

[10] 边新孝，李谋渭.静压空气轴承的动刚度和阻尼分析[J].轴承，2004(12)：1-3.

[11] 舒鹏程.超高速空气静压电主轴的动静态性能分析与实验研究[D].广州：广东工业大学，2011.

[12] LEE J，JANG G，JUNG K.Optimal design of fluid dynamic bearings to develop a robust disk-spindle system in a hard disk drive utilizing modal analysis[J].Microsystem Technologies，2013，19(9-10)：1495-1504.

[13] YANG L，LI H，YU L.Dynamic stiffness and damping coefficients of aerodynamic tilting-pad journal bearings[J].Tribology International，2007，40(9)：1399-1410.

[14] 余鸿钧.流体静压主轴[M].北京：机械工业出版社，1985.

[15] HUANG H，MENG G，LIU L.Nonlinear dynamical analysis of a micro self-acting gas journal bearing[M].Nonlinear Science And Complexity，2007.