基于扩展分形模型的织物组织设计方法
,,,,
(浙江理工大学,a.信息学院;b.材料与纺织学院,杭州 310018)
0 引 言
织物组织用于表现机织物经纱和纬纱相互交错或彼此浮沉的规律,是影响织物的结构、外观以及物理机械性能的重要因素[1]。研究新颖、高效的织物组织设计方法是纺织品设计的一个重要课题。织物组织的数字化设计方法已有很多,如:赵良臣等[2]通过组织矩阵的旋转变换设计织物组织;施国生等[3]将织物组织看作图像,并运用图像变形技术设计新组织;周赳等[4]引入了全息组织的概念,并结合数码技术进行组织设计;金耀等[5]运用置换群表达织物组织,利用代数运算进行织物组织设计。这些方法均从不同的角度建立织物组织的数学模型,不仅提高了设计效率,而且提供了丰富的织物组织类型。
在众多的数字化设计方法中,基于分形的组织设计是其中一类新型的方法。这类方法根据分形几何的思想,借助组织矩阵[2]、图像变换[3]、代数[5]等工具建立数学模型,设计具有层次结构且相互嵌套的分形组织,所设计的组织具有结构复杂、风格多变、不易模仿等特点。现有的分形组织设计方法大致可分为两类:基于L系统法与基于IFS法,分别从分形理论的L系统和IFS的角度设计组织。张聿等[6]首次将分形理论中的L系统引入织物组织设计,运用L系统的链式语言生成规则生成多层次嵌套的分形组织。基于该方法,贾静静等[7]与岑科军等[8]分别针对缎纹组织与3×3平纹,设计出具有特殊纹理效果的分形织物组织。但是这类方法具有一定的局限性,一般要求基础组织具有循环数小且组织点对称布局等特点,其所能设计的组织比较有限。为此,张聿等[9-10]通过Kronecker积运算,运用迭代函数的思想,提出了基于IFS的分形组织设计方法。该方法所设计的组织具有严格的自相似性,是一种特殊的IFS分形组织,突破了L系统的局限性,能够针对任意形式的基础组织设计出对应的分形组织。雷韩等[11]与熊丽丽等[12]采用该IFS法,分别探索了麦粒分形组织与回纹分形组织的设计方法。马铃琳等[13]改进了该IFS法,运用迭代方法在分形组织的不同层次嵌入不同的基础组织,丰富了织物组织的变换形式。章平等[14]则从IFS的定义出发,研究了仿射变换意义下的分形组织,将其中的仿射变换由恒等变换扩充为旋转变换,从而进一步扩展了分形组织的设计空间。上述方法均在分形理论的框架下进行变化,其局部组织的变换形式单一,因此变化空间因此受到限制而有待进一步增大。
本文在现有分形织物组织设计的研究基础上,对其进行进一步扩展,提出了具有一般性的分形织物组织设计方法。该方法基于所定义的组织矩阵的代数运算,将IFS法的仿射变换扩展为一般形式的变换,且增加对填充组织的变化,建立了扩展分形织物组织数学模型。它突破了传统分形织物组织的设计思路,不仅能设计出传统方法所能获得的织物组织,而且具有更大、更灵活的变化自由度,能够设计出传统方法所不能获得的新颖织物组织,从而为织物组织的数字化设计提供了一种新的思路。
1 扩展分形织物组织的数学模型
本文提出的扩展分形织物组织模型是对传统分形织物组织模型的一种推广,其基本思想是增加局部组织的变换形式,包括各种基础组织及填充组织等,为设计者提供更多变化的可能性。本文运用矩阵代数的工具建立扩展分形织物组织的数学模型,首先针对织物组织定义其代数运算。运用Kronecker积描述分形织物组织模型[9-10]的思想,本文同样将织物组织看作布尔矩阵(组织矩阵),并对其定义三种基本的代数运算,由此建立分形织物组织的统一模型。设有组织矩阵(aij)m×n与(bij)m×n,其中aij,bij∈{0,1},则有:
a) 逻辑加⊕:(aij)m×n⊕(bij)m×n=(max(aij,bij))m×n;


fn=A⊗fn-1(n∈N-{0},A∈Wb),f0=A
(1)
由式(1)所定义的递推关系可知,织物组织A的n阶分形组织的结果即对A自身连续施加n次Kronecker积运算:A⊗A⊗…⊗A,本文称之为“Kronecker幂”,记为An。
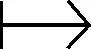

(2)
其中运算优先级⊗高于⊕。
根据生成分形织物组织的数学模型[9-12]可知,分形织物组织由基础组织与填充组织的具体形式唯一确定。其设计过程可分为两大步骤:a) 根据基础组织生成分形组织;b) 运用填充组织生成分形织物组织。因此,分形织物组织可通过对基础组织和填充组织施加变换实现组织结构与形式的变化。
现有数学模型[13-14]的基础组织变换受限于指定的恒等变换或旋转变换,且地填充组织是固定不变的,它们虽然在一定程度上增加了变化形式,但仍未能充分扩大设计空间。为此,本文提出一种扩展的分形织物组织模型。为了方便描述,本文亦将用于设计的组织分为两大类:基础组织Wb与填充组织Wc。它们的含义与其原始定义[6,10]略有不同:基础组织用于生成分形组织的层次结构;填充组织用于对分形组织的组织点进行填充形成最终的织物组织,其中分形组织的经组织点和纬组织点分别填充以不同的组织,在本文中对应地称之为“面填充组织”与“地填充组织”。
由此,本文提出的扩展分形织物组织的数学模型描述如下:

(3)

由该模型的定义(式(3))可见,它是对传统分形织物组织模型的扩展,而后者仅是前者的特例。具体讲,它们存在如下关系:



2 扩展分形织物组织的设计方法
异于传统的分形织物组织设计方法,本文所提出的分形织物组织模型(式3)增加了更多的可控自由度,其组织设计过程也略有区别,具体步骤为:
步骤一:选定基础组织集Wb、填充组织集Wc、分形变换的层数n以及最里层变换函数g,h与其它层组织变换函数rk;
步骤二:从Wb中依次选取n个组织并分别对其施加变换rk,然后再进行分形变换fn-1生成分形组织,其中选取组织的方法可以是人为指定的,也可以是随机生成的(下同);
步骤三:从Wc中选取一个面填充组织,在变换g作用下,按坐标填入分形组织的经组织点;
步骤四:从Wc中选取一个地填充组织,对其进行h变换后按坐标填入分形组织的纬组织点。
在上述步骤中,关键是组织集的选取、分形层数确定以及变换函数的设计。
基础组织决定分形组织的整体结构。在选取基础组织集时,织物组织的组织循环数的大小和组织点分布形式可以自由选取,如可以是常见的规则组织和不规则组织。填充组织的作用是为防止浮点过长,对组织最终形成的肌理效果影响较大,理论上它也可以选取各类组织。但是考虑到局部组织的变换,为使得组织便于在固定大小的空间内进行“填充”,基础组织和填充组织的循环数需满足一定的约束:对于Wb中的组织,其循环数可互不相同;但对于Wc中的组织,其循环数均需相同。
分形层数n很大程度上决定了分形组织结构的复杂性。当n=0时,即为原组织本身;当n>0时,便出现层次嵌套的现象,n越大层次越深,分形组织的结构也越复杂。分形层数一般根据实际设计意图和需求确定,通常取作:3≥n≥1。
变换函数决定了肌理的复杂性与多样性。变换函数可以根据基础组织与填充组织的特点进行设计。例如可以将组织看作几何图形进行旋转变换,亦可以将组织看作矩阵进行转置变换等。此外,变换函数不仅可以对同层组织施加同一种变换,也可以对各个组织点分别进行独立变换,即可设计关于组织点坐标的任意函数,因此其设计空间非常大,也非常灵活。但需要注意的是变换rk、g和h均不能改变原组织的循环数。
3 实 验
本文在Visual C++2017开发环境下实现了分形织物组织的生成算法,其中采用Eigen库实现组织矩阵的存储与运算,并运用MFC的文档与视图框架实现组织意匠图的可视化。


图1 本文算法生成的分形织物组织注:其中组织(a)上方的两个小组织分别生成下方的基础组织与地填充组织;(b)、(c)上方四个组织中前两个是基础组织,第三个是面填充组织,第四个是地填充组织。
与传统的IFS模型及其变种[10,13-14]比较,本文提出的扩展分形织物组织模型具有更大的优势,它所能设计的组织空间更大,既能够设计出传统方法所能设计的组织,也能设计出传统方法不能设计的组织。下面给出两个例子进行说明。



图2 不同变换生成的分形组织图
本文方法增加了对地填充组织的变化。传统方法在设计分形织物组织时,所用的“填充组织”,即对应本文的地填充组织均是单一不变的,而本文方法可对地填充组织进行选择性地变化。该变化形式取决于用户所给的变换hij(见式(5))。除了采用常用的旋转变换外,亦可以采用其它形式的变换,例如上述的转置变换。图3给出了由(a)某分形组织配合由三个函数l(i,j)=0,l(i,j)=i+j


图3 不同变换算子作用下所形成的分形织物组织
本文算法的时间复杂度是O(m2(n+1)),其中m是输入基础组织和填充组织的平均组织循环数。该算法尽管采用了Kronecker积定义分形织物组织,但实际计算时并不直接根据Kronecker积的运算法则进行,而是利用组织矩阵的特点,仅在组织矩阵元素为1的位置填充组织,从而避免了大量的乘法计算,节省了计算时间。大量实验表明,对于生成一般的分形织物组织(基础组织与填充组织的循环数小于10,层数小于3),本文算法均能达到实时响应的速度,能够满足交互设计的需求。
4 结 论
本文提出了基于扩展分形模型的织物组织设计方法。该方法基于代数运算,并引入针对组织的各种变换算子,建立了具有一般性的分形织物组织模型,并提出了基于该模型的分形组织设计方法。计算机仿真实验表明,运用该方法进行组织设计是可行的。它提高了组织设计的自由度与灵活性,能够设计出比传统方法更为复杂多变的组织;从而更进一步拓展了组织设计的空间,为分形织物组织设计提供了新的思路。在今后的工作中,将引入更多的变换算子并研究变换算子对最终形成的组织外观的影响规律。
参考文献:
[1] 蔡陛霞.织物结构与设计[M].北京:中国纺织出版社,2008:32-40.
[2] 赵良臣,闻涛.旋转组织设计的数学原理[J].纺织学报,2003;24(6):33-4.
[3] 施国生,张瑜秋,熊超.图像变换在多臂织物组织设计上的应用[J].纺织学报,2006,27(7):23-26.
[4] 周赳,吴文正.基于数码技术的机织物组织设计原理和方法[J].纺织学报,2007,28(4):48-51.
[5] 金耀,张聿.织物组织的群表达方法[J].纺织学报,2010,31(6):48-51.
[6] 张聿,金耀,孙家武,等.基于L系统的织物分形组织设计方法[J].纺织学报,2007,28(5):51-54.
[7] 贾静静,张聿.基于L系统的缎纹分形组织及其织纹效果设计[J].丝绸,2011;48(5):32-4.
[8] 岑科军,贾静静,孙家武,等.基于L系统的3×3平纹分形组织设计应用方法[J].纺织学报,2011,32(11):49-52.
[9] ZHANG Y, Han L. Design method of plain fractal weave based on IFS & Kronecker product[C]//2011 4th IEEE International Conference on Computer Science and Information Technology (IEEE ICCSIT 2011 ).IEEE,2011:401-404.
[10] 张聿,金耀,岑科军.基于IFS的非规则分形组织设计方法[J].纺织学报,2012,33(12):30-34.
[11] 雷韩,张聿.基于IFS确定性迭代算法的麦粒分形组织设计法[J].丝绸,2012;49(8):26-9.
[12] 熊丽丽,张聿.基于斜纹基本组织的回纹分形组织设计方法[J].丝绸,2015,52(1):31-34.
[13] 马铃琳,张聿.各层基础组织互异的分形组织设计方法[J].丝绸,2013;50(9):45-9.
[14] 章平,张聿.同层仿射分形织物的设计方法[J].丝绸,2014;51(12):35-8.

