回溯算法案例分析

冯建

摘要

回溯算法是《数据结构与算法》课程中介绍的一种广泛应用的搜索策略算法，本文作者在长期教学实践中总结出一套实用的回溯算法的框架。本文描述回溯算法的基本思想，分析回溯算法的基本框架，通过案例详细介绍回溯算法的实现过程，进一步验证回溯算法程序框架的可行性。对回溯算法的分析总结，有助于加深对回溯算法的理解，提升程序设计的能力。

【关键词】回溯 算法 案例

回溯算法是一种搜索策略算法，是一种从问题的解空间中寻找可行解或最优解的一种算法。它广泛应用于各种软件系统的开发。应用回溯算法的经典案例有：猎人过河、分油问题、八皇后问题等。探讨回溯算法的基本框架，对加深回溯算法的理解，增强编程兴趣，提高编程能力具有重要意义。

猎人过河问题：一个猎人带一匹狼、一只羊和一捆草来到河边，河边有一条小船，只有猎人会撑船，而且小船每次最多只能带一样东西过河。当猎人不场时，狼会吃羊，羊会吃草。问猎人该如何过河，才能使狼、羊、草全部安然到达河对岸。

分油问题：现有三件无油量刻度的油瓶，容量分别为10斤、7斤和7斤。其中，10斤容量油瓶装满油。如何操作，才能将10斤油平均分成两份。

1回溯算法的基本思想

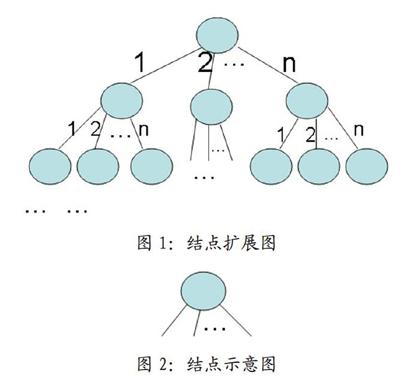
猎人过河问题、分油问题都可以归结为一个结点沿着不同方案扩展为新结点的演变过程。如图1所示，从初始状态（根结点）有若干个方案向子结点扩展，每个子结点又有若干个方案向新的子结点扩展。依此类推，构成树状结构图。

回溯算法寻找目标结点的基本思想是：每次优先选择第一个方案向下扩展，直到新产生的结点不合理或己产生过，再返回上一结点，若此时存在下一个未扩展方案，则选择下一个方案继续依此向下扩展，否则，继续回退。直到找到目标结点或所有方案均穷尽为止。

2回溯算法的程序框架

2.1回溯算法的描述

设结点的扩展方案为n个。

（1）从当前结点current Node依次从方案1到方案n尝试扩展新结点。

（2）每当产生的新结点合理时，就立即从新结点依次从方案1到方案n扩展新结点。

（3）当某结点所有方案均已扩展，并且未找到目标结点，则该结点视为不合理结点。

（4）直到找到目标结点或所有方案扩展完毕为止。

2.2回溯算法的结点结构

以下利用C语言格式的伪代码描述回溯算法的程序框架。首先，将状态值与该状态已扩展的路径编号合在一起，定义成状态结点。如图2所示。

结点结构定义如下：

struct node

{

状态值：

int path; //上一次搜索过的路径编号

};

typedef struct node State;

2.3回溯算法的非递归程序框架

对回溯算法的求解，通常可以使用递归与非递归方式。借助栈的结构，可利用非递归方法实现回溯算法，其程序框架如下：

int total_path;//总方案数

State current，new_node;//定义变量

current-初始状态值：

current.path=0;//初始，己扩展的方案为

push（current）;//当前结点进栈

while（栈非空）{

currenFpop（）;∥出栈

if（current.path！=total_path）{ //该结点可扩展

current.path++;

push（current）;

∥进栈

new_node=createNew（current）;//扩展新结点

if（new_node==最终目标）{

输出栈中元素及最终目标。

程序结束;

}

else if（new_node与栈中元素不相同，并且new node是合理的）{

new_node.path=0;

push（new_node）;

}

}

}

2.4回溯算法的递归程序框架

回溯算法本质上是深度优先搜索，具有明显的递归特征，可利用递归的方法来实现。从当前出结点出发搜索目标结点的函数记为：dfs（State current），程序框架如下：

void dfs（State current）{

if（current==目標结点）

{

打印栈中元素，程序结束。

}

else{

for（i-1;i<-总方案数;i++）{

new_node= createNew（current，i）;∥按方案i扩展新结点

if（new node是合理结点，并且不与栈中元素相同）

{

push（new_node）;∥新结点进栈

dfs（new_node）;//从新结点开始搜索

pop（）;//出栈恢复现场

}

}

}

}

3回溯算法的案例分析

以下利用“猎人过河”案例，描述回溯算法非递归程序的具体实现过程。本程序为突出算法框架，省略对栈空及栈满判断等细节。结构体中h（human）代表人，w（wolf）代表狼，s（sheep）代表羊，g（grass）代表草。状态值O表示未过河，1表示己过河。

#define MaxSize 10000

#define total_path 4

struct node

{

int h，w，s，g;//分别代表人、狼、羊、苴

int path; //上一次搜索过的路径编号

};

typedef struct node State;

struct stackf

State data[MaxSize];

mt top;

};

typedef struct stack Stack;

void push（Stack* s，State current）{//进栈，本处省略栈满情况

s->top++;

s->data[s->top]=current;

}

State pop（Stack* s）{ //出栈，本处省略栈空情况

State current;

current=s->data[s->top];

s->top--;

return current，

}

State createNew（State current）{//擴展新结点

State newState，

int path=current.path;

newState=current;

newState.path=0;

newState.h=（newState.h+l）%2; //人总要过河

if（path==l） newState.w=（newState.w+1）%2;//人带狼过河

else if（path==2） newState.s=（newStates+11%2;//人带羊过河

else if（path==3） newState.g=（newStateg+1）%2; 11人带草过河

return newState;

//path=4时，只有人过河

}

int reasonable（State st）{

//判断当前结点是否合理

if《st.w=st.s）&& （st.w！=st.h》 return 0;//人不在，狼吃羊

else if《st.s==st.g）&& （st.s！=st.h》 retumO;//人不在，羊吃草

else return 1：

}

int isSame（Stack* s，State cur）{//判断当前结点在栈中是否存在

mt1：

State St：

for（i=O;i<=s->top;i++）{

st=s->data[i];

if（st.h==cur.h&&st.w==cur.w&&st.s==cur.s&&st.g==cur.g） return 1;//当前结点以前产生过

}

return 0：

}

void prt（Stack*s）{//打印栈中元素

mt1;

State St：

for（i=O;i<=s->top;i++）{

st=s->data[i];

printf（”（%d，%d，%d，%d）—“，st h，st W，st.s，st g）;//输出人、狼、羊、草的状态

}

}

in main（）{

State current， new_node;//定义变量，goal为目标结点。

Stack s;

s.top=-l;//初始栈为空栈

current.h=0;

current.w=0，

current.s=0;

current.g=0;

current.path=0; //初始，己扩展的方案为O

push（&s，current）;//当前结点进栈

while（s.top！=-l）{//栈非空

current=pop（&s）;∥出栈

if（current.path

current.path++;

push（&s，current）;

//进栈

new_node=createNew（current）;//扩展新结点

if（new_node.h*new_node.w*newnode.s*new_node.g==l）{//找到目标结点

pn（&s）;

printf（"（1，1，1，1）"）;//输出栈中元素及终点状态

retum0：

}

else if《！isSame（&s，new_node》&&reasonable（new_node》{

push（&s，new_node）;

}

}

}

}

程序运行结果按人、狼、羊、草的状态输出。0表示未过河，1表示己过河。运行结果如下： （0，O，O，0）一（1，0，1-o）一（0，0，1，0）一（1，l，1，0）一（O，1，O，0）一（1，1，O，1）一（O，1，0，1）一（1，1，1，1）

上述程序也可利用递归的方法来实现，同样，可以利用回溯算法的程序框架，解决分油问题、八皇后问题等。程序不再赘述。

4结束语

回溯算法是应用较为广泛的搜索算法，在具体应用中具有较大的改进与优化空间。本文提出回溯算法的基本框架，并用实例验证该框架的有效性。对初学者应用回溯算法解决问题具有借鉴意义。也为后续进一步学习分枝限界法等其它算法打下良好的基础。

参考文献

[1]程香，用回溯算法诊断数据库性能故障[J].长春师范大学学报，2015，34 （12）：30-34.

[2]高小芳.回溯算法在可视化物流配送最优路径规划模拟软件中的应用[J]，聊城大学学报（自然科学版），2017，30 （04）：101-106.

[3]李志伟，曹阳，张凯，数据结构中八皇后问题的堆栈非递归方法的实现研究[J].福建电脑，2012 （02）：115-116.

[4]王永建，铁小辉，董真等，一种人工智能搜索算法的改进研究[J].通信技术，2017， 50 （02）： 248-254.

[5]申云成，赵莉，顾庆传，基于C语言的递归算法分析[J].福建电脑，2015 （06）：133-134.

[6]任小康，吴尚智，苟平章，基于动态状态树的回溯算法[J].计算机工程与设计，2007， 28 （04）： 755-756.