一个新四翼忆阻混沌系统的设计与性能分析

雷宇

摘要

将一个基于双曲函数的非线性函数应用于三次磁控忆阻混沌系统得到一个四翼吸引子混沌系统，通过吸引子相图、lyapunov指数分析表明，该多翼混沌吸引子具有更丰富，更复杂的动力学特征，仿真结果和理论计算一致，为新的混沌电路的设计提供了一种思路。

【关键词】连续非线性函数 忆阻混沌系统 混沌吸引子 lyapunov指数

1982年，蔡少棠提出了著名的蔡氏电路，在一定参数条件下，可产生各种分岔、单涡卷和双涡卷混沌吸引子等非线性现象和混沌动力学行为[1-2]。Itoh和蔡少棠[3]利用一个分段线性的忆阻器替换蔡氏混沌电路中的蔡氏二极管，得到第一个忆阻混沌振荡路。Muthuswamy[4]将一个不连续分段线性忆阻器代替蔡氏电路中的二极管，得到新的混沌行为。

包伯成基于一个具有光滑连续的三次单调上升的磁控忆阻器设计出忆阻混沌电路，具有丰富而独特的动力学特性[5-6]。自1993年suyken等成功构造多涡卷系统后，许多学者分别采用分段线性函数、时滞函数、正弦函数和饱和函数[7-10]在Lorenz系统[11-13]、Jer[14]、colpitts[15]等不同混沌系统构建了更为复杂的多涡卷吸引子，被广泛的应用于保密通讯、信息加密、数字语音等信息领域，这种获得更为复杂的混沌吸引子的方式也日益被关注。

本文设计了一个基于双曲函数的连续非线性函数，将此函数应用于三次光滑忆阻混沌系统，对新系统进行动力学分析，并对其进行matlab仿真仿真，结果与数值计算结果一致。2新的四翼忆阻混沌系统的设计

（1）包伯成构建的光滑忆阻混沌系统的动力学方程为：

x=A[y-x+Dx-W（w）x]

y=x-y+z

z=-By-Cz

w-x

W（w）忆阻器忆导，W（w）=a+3bw2，式（1）中：x，y，z，w为状态变量，A，B，C，D，a，b为系统参数。当选择参数A=16.4，B=15，c=o.5，D=1.4，a=0.2，b=0.4时，系统（1）存在一个典型的两涡卷混沌吸引子，如图1所示。

（2）构建一个基于双曲函数的非线性函数，表达式为：

F=k*z-p*k*（-tanh（n*z）+tanh（n*z）+tanh（n*（z+2 *p》+tanh（n*z）+tanh（n*z-2 *p》

此函数由线性函数和非线性函数合成，是连续的，k分别为0 65和0 35时非线性函数F（z）的曲线图如图2所示，由图1可知，k可改变非线性函数的斜率。

（3）将非线性函数引入到系统（1）第4式，从而构建了如下的新的忆阻混沌系统（2）：

x=A[y-x+Dx-W（w）x]

y =x-y+z

z=-By-Cz

w=x+k+z—p*k*（-tanh（n*z）+tanh（n*z）+tanh（n*（z+2*p》）+tanh（n*z）+tanh（n*z-2*p》

3新系统的动力学分析

3.1对称性

新系统作变换（x，y，z，w）一（-x，-y，-z，-w），系统保持不变，即系统关于原点对称，这种对称性，对于所有参数都成立。

3.2耗散性

散度

vv=

此时系统是耗散的，当在此条件下，当t趋近于无穷大时，系统轨线上每一个小体积元收敛到零，系统的轨道逐渐趋于一个吸引子。

3.3混沌吸引子，lyapunov指数和维数

设新混沌系统初始值为（O.l，0.1，O.l，O.l），在matlab中应用龙格.库塔法进行数值计算可以得到吸引子相图，利用wolf方法可以得到李雅普诺夫指数。

固定，时间步长为0.5，最大时长为400，新系统混沌吸引子如图所示，由图可看出：相比单向两涡卷混沌系统相比，该系统在多方向上分离产生四翼吸引子，具有更复杂的动力学行为。

3.3.1固定P=5，n=30，k=0.95

设时间步长为0 5，最大时长为400，新系统混沌吸引子如图3所示，由图可看出：相比单向两涡卷混沌系统，新系统相轨在更多方向上分离，在不同方向拉伸折叠变换，产生四翼吸引子。当初始值为（0.1，O.l，O.l，O.l），时间步长为0 5，最大时长为400，李雅谱诺夫指数为LEl=0.104657，LE2=0，LE3=-0 851344，LE4=-19.664244，系統的维数为：

Ei= 2.0051，系统lyapunov指数一个为正，一个为O，两个为负，且lyapunov维数是分数，因此系统在此参数下是混沌的。

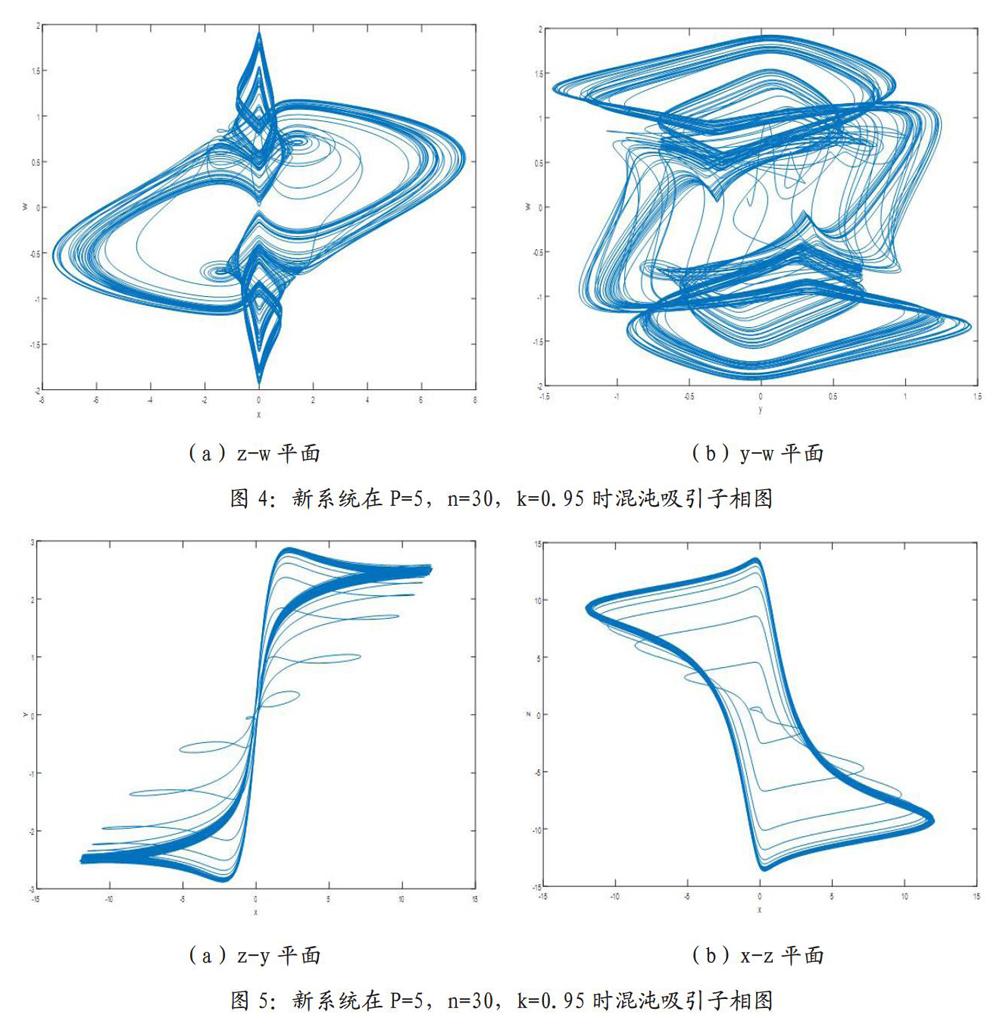
3.3.2固定P=5，n=3，k=0.4

新系统的混沌吸引子如图所示4。新系统相轨同样产生四翼吸引子，但吸引子在x和方向收缩。当初始值为（O.1，O.l，O.l，O.l），时间步长为0.5，最大时长为400，李雅谱诺夫指数为LEl=0.167547，LE2=0，LE3=-0.792802，LE4=-17.720023，系统的维数为2 0092，系统lyapunov最大正指数相比参数为P=5，n=3，k=0.95时的状态更大，且lyapunov维数是分数更大，因此系统在此参数下是混沌复杂度增大。

3.3.3固定P=5，n=30，k=-0.2

新系统的混沌吸引子如图5所示。新系统以周期轨道运行。当初始值为（O.l，O.l，O.l，O.l），时间步长为0 5，最大时长为1200，新系统李雅谱诺夫指数为LEl=-0.072336，LE2=-0.131838， LE3=-0.331302， LE4=-26.192317，新系统lyapunov指数一个为O，三个为负值，可以说明系统处于周期态。

4结语

本文在一个二翼忆阻混沌系统的基础上提出了一个新四翼混沌系统，利用理论分析和matlab数值计算分析了新系统，其既能产生不同形状的四翼吸引子，也能得到周期性轨道，具有更加丰富的动力特征。为获得新的混沌系统提供一种思路，在保密通信中的信息加密具有较高的应用价值，为在通讯安全领域的应用提供可行性依据。

参考文献

[l]Chua L O， Komyro M， Matsumoto T.The Double Scroll Familiy[J].IEEE Transactions on Circuits andSys tems，

1986， 33 （11）： 1072-1118.

[2]Chua L O， Lin G N. CanonicalR ealization of Chua' s CircuitFamily [J]. IEEE Transactions onCircuits and Systems， 1990， 37 （7）： 885-902.

[3]1toh M， Chua LO. Memristoroscillators [J]. Int J Bifur Chaos，18： 3183-3206.

[4]Muthuswamy， B， and Kokate， PP.Memristor-Based Chaotic Circuits [J].IETE Tech.

Rev.，

2009， 26 （6）： 417-429.

[5]包伯成，胡文，许建平，刘中，邹凌，忆阻混沌电路的分析与实现[J].物理学报，2011， 60 （12）：120502.

[6]包伯成，刘中，许建平，忆阻混沌振荡器的动力学分析[J].物理学报，2010， 59 （06）： 378509.

[7] Yuan Fang， Wang Guangyi， WangXiaowei. Extreme multistabilityin a memristor-based multi-scrollhyperchaotic system[J]. Chaos，2016，2 6 （7）：1-10.

[8] Henry Alombah N， HilaireFotsin，MegamNgouonkadi E B， et al. Dynamics，analysis and implementation ofamultiscrollmemristor-basedchaotic circuit [J]. InternationalJournal of Bifurcation and Chaos，2016，26 （8）：1650128：1-20.

[9]Hu Xiaoyu， Liu Chongxin， Liu Ling， etal.

Mult i-scroll

hidden attractorsin improved sprott a system[J].Nonlinear Dynamics，

2016， 86 （3）： 1725-1734.

[10] Sajadjafari， Viet-Thanh Pham，Tomasz Kapitaniak. Multiscrollchaotic sea obtained from a simple3D system without equilibrium[J].International Journal of Bifurcationand Chaos， 2016， 26 （2）： 1-7.

[11]艾星星，孫克辉，贺少波.不同类型混沌吸引子的复合[J].物理学报，2014， 63 （04）： 040503.

[12]孙克辉，傅元理，简化Lorenz系统多翅膀混沌吸引子的设计与电路实现[J].动力学与控制学报，2016，14 （05）： 395-400.

[13]艾星星，孙克辉，贺少波，王会海，简化Lorenz多涡卷混沌吸引子的设计与应用[J].物理学报，2014，6 3 （12）：120511.

[14]王雅丽，李志军等，电流型网格多涡卷混沌电路的设计与实现[J].微电子学，2017， 47 （02）： 226-232.

[15]王振宇，苏咏梅，一种网格多涡卷混沌Colpitts振荡器及其电路实现[J].电子器件.2017，40（06）：1441-1444.