iGPS导航技术的探索分析研究

张佩华，吕红丽

（1 中国电子科技集团公司第二十研究所，西安 710068；2 陕西省组合与智能导航重点实验室，西安 710068）

0 引言

铱星系统是摩托罗拉公司于 1998年建设完成的全球通信系统，分布卫星数量多，在全球任意区域可见卫星数是1～3颗；铱星系统空间段包括72颗星，分别分布在6个倾角为的极地轨道面上，每个轨道面包括11颗业务星和1颗备份星。业务星轨道高度是780km，轨道周期100min，飞行速度27070km/h；备份星留轨高度是677km，留轨以随时顶替不能服务的业务星。

铱系统卫星属于低轨通信卫星，运动速度大，在空中几何构型快速变化，信息速率高，信号功率高，不易被干扰，铱系统与GPS L1频率接近，可共用天线。

基于铱星系统的以上特点，2002年，美国波音公司提出了将 GPS与铱星系统相结合的增强导航系统，即iGPS（the High Integrity GPS），所以iGPS是一个 LEO-MEO卫星结合的导航和授时系统；2007年，波音公司针对iGPS进行抗干扰测试，iGPS能抵抗恶意和无意干扰，对美国军方很有吸引力，并着手下一代Iridium Next系统的建设；2009年，iGPS验证了在运动车辆受到强烈干扰环境下的捕获GPS信号的能力；2013年，铱星公司计划在下一代卫星上装载iGPS载荷，播发宽带扩频码信号，

地面参考站和铱星地面终端接收过境的 GPS卫星和铱星卫星的信息，传输给操控中心，操控中心确定铱星星历和钟差数据，上注给铱星卫星。

铱星卫星过境时间相对较短，持续 10～20分钟，但接收功率比中高轨导航卫星强，每个卫星分配有卫星（SV）编号，所以在导航终端一般可见卫星不足3颗，拟采用多普勒测量进行定位。

iGPS工作方式为：

可以利用铱星卫星和GPS卫星联合解算，改善用户观测几何因子，比普通GPS用户几何因子可以改善30%；

低轨卫星的大多普勒和相对于导航用户终端的几何构型变化快，用户观测数据几何变化明显，可加快接收机载波相位整周模糊度收敛速度，支持快速获得高精度定位结果，定位收敛时间由20～30分钟缩短至 2～3分钟；整周模糊度是利用其在一段连续观测时间内保持不变的特点，基于不同时间内多个观测数据进行解算确定，如果观测数据变化快则整周模糊度收敛快，否则收敛速度慢。收敛速度可简单的描述为与卫星和接收机连线划过的角度正相关，相同时间划过角度越大则收敛越快。如图3所示，低轨卫星的轨道高度是780km，运行速度为8km/s左右，GPS卫星高度20000km左右，运行速度4km/s左右。相同时间低轨卫星划过的角度是GPS的60倍左右，因此在相同的可见卫星数条件下，铱星的载波收敛速度是GPS的60倍左右。

图3 观测数据变化图

1.2 iGPS系统时间同步设计

铱星载荷上采用成本较低的晶体振荡器来生成通信信号并维持系统时间。短时间间隔内，这些时钟非常稳定，但是时间超过100s，这些时钟的偏置和漂移比GPS卫星使用的原子钟不稳定的多，所以铱星的钟差和钟漂每天至少要和地面校正两次，所以铱星每天至少需要两次时间同步与地面站进行钟差和钟漂校正，钟差和钟漂比较大的铱星可以被多次校正。iGPS系统的时间同步结构建立除了GPS卫星和铱星外，还包含地面参考站、控制中心和铱星用户终端等，用于收集过境星信息再转发到控制中心。为了有效地将铱星星座用于GPS的增强，必须知道铱星的位置，并且必须准确地估计铱星时钟及相对于GPS系统的时差。铱星之间使用星间链路获得铱星星间相对时差，并通过下行链路传递给的参考站；每个地面参考站使用单频GPS L1并配有铷钟的接收机校准到GPS系统时，同时获得铱星下行链路测量数据。这样，所有地面参考站收集了参考站与GPS系统的时差测量数据、与铱星的时差测量数据以及铱星星间时差测量数据，通过地面网络控制链路送操控中心进行综合处理，从而获得铱星的星历和时钟偏差通过上行 K波段通信链路注入铱星。其时间同步结构如图4所示。

图4中地面参考站与GPS系统之间的时差可通过高精度GPS测量接收机实现，其精度可达到10～20ns，比下行链路测量误差小得多。这里铱星的钟差和下行链路测量误差才是系统的主要误差。其下行链路时差测量误差模型为：

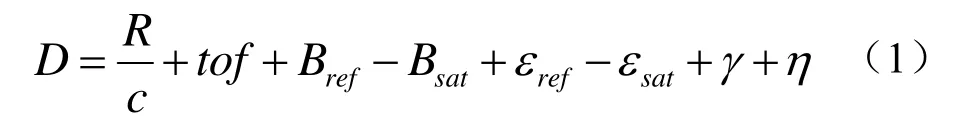
其中，R为铱星与地面参考站之间的几何距离，tof为铱星运动带来的误差，Bref为参考站的钟偏，Bsat为铱星钟偏，εref为参考站接收机硬件偏差，εsat为卫星发射机硬件偏差，γ包括电离层和对流层延迟误差，η表示所有其他误差。

采用地面参考站和铱星的已知位置，可消除式（1）的几何距离和铱星运动带来的误差，同时采用高精度GPS测量可消除地面站的钟偏，因此下行链路时差测量的残留误差为：

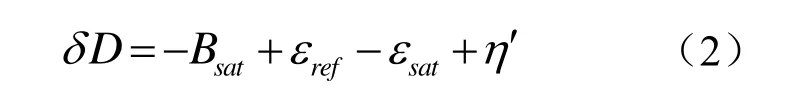
其中，η′为包含电离层和对流层残留误差、残余星历误差、多径及下行信号测量等，通常该残留误差不超过50ns[2]。

因此，iGPS系统时间建立是基于铱星星载廉价的晶振、GPS信号的载波测量以及地面参考站网络的误差修正相结合而合成的高稳定时钟模型结构。

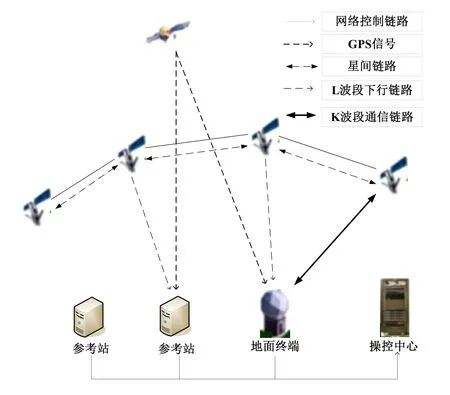
图4 iGPS时间同步结构图

1.3 iGPS导航用户终端的多普勒测量定位

因为 iGPS卫星导航系统卫星轨道高度低、运行速度快，与用户终端之间产生很大的多普勒频移，给用户终端的解调带来了很大困难，降低了导航系统性能。为保证可靠稳定的信号跟踪，必须获取卫星在可视范围内对用户终端的多普勒频偏和变化规律，并给出相应补偿，实现快速跟踪解调。并在用户终端的环路设计中采用高动态的捕获与跟踪算法，尽力减少捕获时间，快速实现稳定跟踪，获得连续可靠的多普勒测量值和导航电文信息。

接收低轨卫星信号的瞬时频率f为：

f0为低轨卫星信号的载波频率，fd观测多普勒频率[3]。其中，多普勒频率

其中，r˙(t)是卫星与用户之间距离的导数，即相对运动速度，如图 5。假定卫星与用户距离方向上的单位矢量则第i时刻的r˙(t)可以通过式（6）建立与目标坐标之间的关系，即

其中，为卫星位置。

由此，根据式（3）、式（4）和式（5），第i时刻用户终端测量第i颗星得到的多普勒测量值为：

其中，

而ζi是第i时刻测频的噪声，各个时刻的测频噪声服从独立的高斯分布。

将同一时刻的N个测量信息用矩阵的形式表示为：

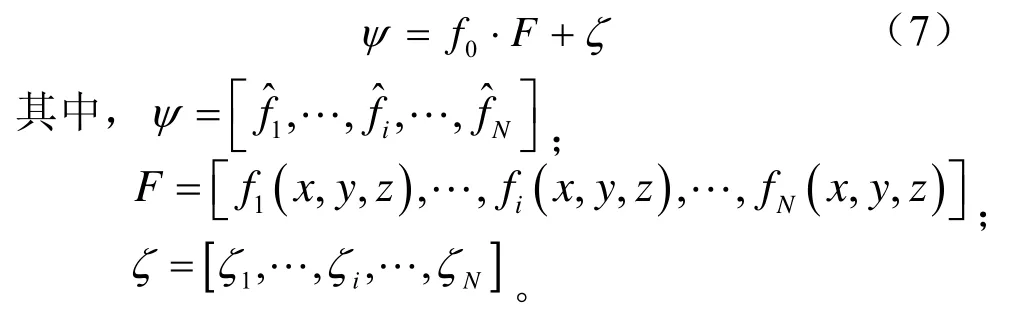
根据式（6）解算用户位置(x,y,z)和测频噪声ζi，存在四个未知参数，因此需要获得同一时刻至少四颗可见卫星的多普勒测量值才能解算用户的精确位置。针对低轨卫星快速运动的特点，在可见卫星数小于方程未知数时，如图5所示，可通过对同一颗卫星进行连续多次测量，总测量次数大于等于方程未知数，获得用户位置。

图5 多普勒定位原理图

这种定位原理是基于低轨卫星高速运动的特点，主要针对低动态用户在短时间间隔内可以获得多次多普勒测量值，且多普勒测量值变化较大，从而获得较好GDOP分布，实现高精度用户定位。

2 iGPS试验验证

由于不能对在轨的铱星系统进行改造，iGPS系统试验采取转发模式，地面处理生成差分和测距信号，利用铱星下行通信信号转发给用户。

图6 iGPS静态试验测试结果

利用铱星空间几何构型迅速变化的优势，可进行载波相位测量的整周模糊度的快速解算。在精密单点定位（PPP）模式下，车辆动态定位，首次定位时间由30分钟缩短至2分钟，定位精度为亚米级。如图6是静态测试结果，水平测试误差小于6cm。图7是动态试验测试轨迹。

图7 iGPS动态试验测试轨迹

铱星卫星高速运行，快速变化的观测数据，可以增加 iGPS用户测量的卫星数量，改善可用性。尤其是在城市峡谷、山区等地方将获得更高的可用性，iGPS用户可见卫星数量增加至少两颗，HDOP值则改进30%以上，如图8所示。

图8 采用铱星和GPS联合解算后HDOP的改善

3 iGPS的特点和意义

iGPS依托美国强大的航天体系优势，通过卫星导航与卫星通信的融合提供性能优化的导航增强服务，是航天体系应用的经典案例；采用资源整合和综合利用方式，主要以软件形式实现增强，性价比十分突出；增强效果良好，重点实现了最为关键的定位精度和抗干扰能力的大幅度增强，极大地增强了GPS系统服务性能；iGPS在美国导航体系中的位置如图8所示，重点提供厘米级到米级的定位精度，但是由于 iGPS系统属于在轨资源的综合利用，第一阶段方案实现受限于低轨通信卫星转发体制，需依赖地面设施支持，系统灵活性存在不足。

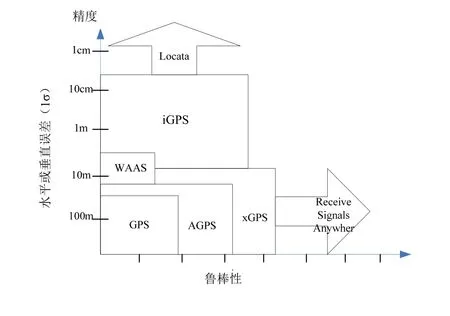
图9 美国导航体系构架图

4 结论

通过 iGPS系统探索分析研究，对类似低轨星导航应用系统会有诸多启示。

首先，在工作体制上，利用低轨卫星构建导航系统可以采用直发信号体制和直发加转发信号体制两种模式，直发信号体制是自己播发导航服务信号，转发信号就是转发中高轨导航卫星的导航信号，增强信号功率，提高抗干扰能力。

其次，在导航终端方面，导航终端可采用多普勒独立定位，这样在可见星布局少的情况下也可以完成定位解算；另外一种模式就是在利用低轨卫星增强中高轨卫星的时候，充分利用低轨卫星观测数据快速变化特点，可支持用户直接利用载波相位观测数据参与定位解算，快速获得高精度定位结果。

最后，iGPS对低轨卫星导航应用系统建设的借鉴经验，低轨星导航系统可以作为一个独立的导航系统，也可以成为对中高轨卫星的增强系统，但是为了增加低轨星导航系统的灵活性，在卫星定轨和时间同步方面尽量采用星载GNSS接收机和星间链路实现自主计算，减少对地面站点的依赖，以提高系统自主运行能力。

参考文献：

[1]David Whelan. iGPS: Integrated Nav& Com Augmentation of GPS Boeing Defense Space & Security& Dr.Per Enge, Stanford University Dr.Greg Gutt, iKare Corporation November 2010.

[2]John Pratt.PeninaAxelrad.Kristine M.Larson.Bruno Lesage.Richard Gerren.Nicholas DiOrioSatellite clock bias estimation for iGPS GPS SolutDOI 10.1007/s10291-012-0286-4

[3]潘磊.基于多普勒频差的机载无源定位技术研究[D].西南交通大学, 2013.