基于地理邻近性的自编码器在地点推荐中的应用

张文翔

(天津大学管理与经济学部,天津 300072)

0 引 言

伴随着基于位置的社交网络(Location-based Social Networks, LBSNs)的快速发展，例如Foursquare，Brightkite和Gowalla等，签到行为成为用户分享生活的关键途径之一[1]。因此，从用户的签到数据中挖掘用户的兴趣偏好——用户地点推荐吸引了诸多学者的关注。个性化地点推荐不仅可以节省用户时间，提高用户满意度，而且有利于商家的定制化营销[2]，因此，个性化地点推荐已经成为LBSNs发展中比较重要的一个方面，关于这方面的研究至关重要。

以往研究中，往往将所有的地点(Point of Interest, POI)同等看待，这就意味着用户一周去6次博物馆，与一周去6次超市同等看待，但是去超市比较常见，经常去博物馆极为少见，不可同等看待。因此，本文根据权重分析理论TF-IDF，将签到频率转换为基于类别的用户偏好。与传统推荐任务不同的是，在POI推荐领域，最重要的就是地理影响[3-5]。如地理学第一定律所陈述“任何事物都相关，但是相近的事物之间关系更密切”，相近的POI之间更有可能具有密切的联系，这种联系叫做地理邻近性。因此，对地理邻近性进行建模，对于个性化地点推荐至关重要。在过去的几年里，深度学习由于在特征挖掘方面的巨大优势，在机器智能领域取得了巨大的成功[6]。在地点推荐系统中，挖掘有效的地点特征是算法的关键。因此在本文中，利用深度自编码器处理地点推荐任务。

1 地点推荐系统的研究现状

1.1 地点推荐系统

LBSNs中地点之间存在地理邻近性，而且很多研究发现，在LBSNs中的用户签到的POI分布上，存在某种地理聚集现象。例如，有部分学者根据用户的签到数据发现，被同一个用户签到的POIs的距离服从统一的分布，即幂律分布，因此可利用幂律分布计算POIs之间的关联，最后用于预测用户对于POI的推荐列表[7-9]。也有学者发现用户的签到行为集中在几个中心地区，因此可利用多中心高斯分布对用户签到的POI进行建模，之后结合基于模型的协同过滤算法[3]。而文献[10]利用基于二维地点坐标的核密度分布对地理邻近性进行建模，同时结合二维核密度分布，形成基于模型的地点推荐系统。

本文尝试采用一种新的方法对地理信息建模，利用基于地理邻近性的深度自编码器模型对POIs之间的关系进行建模，提取POIs之间潜在关系和特征。

1.2 深度学习与地点推荐

作为一种表示学习方法，深度学习具有多层表示结构，每一层由许多简单的非线性单元组成，且每个单元可以将底层的表示转化到更好、更抽象的层级[6]。深度学习技术，由于在特征提取上的强大优势，已经被应用于多个领域，但是深度学习技术在推荐系统领域的研究刚刚起步，还没出现系统化的研究。最早利用深度学习相关技术研究推荐系统的是利用受限玻尔兹曼机组成的协同过滤技术形成推荐算法[11]，但是该方法不适用于地点推荐。

最近一些学者逐渐开始研究深度学习技术在地点预测领域的应用。例如，在文献[12]中，作者提出一种空间嵌入模型对LBSNs中的签到数据进行建模，与深度学习处理词向量的词嵌入方式类似，该方法利用深度学习技术对签到数据进行嵌入处理。该方法的关键是将多个上下文信息(用户、地点、时间等)融合在同一个模型中，并嵌入到同一个表示空间，即利用同一个嵌入空间表示多种上下文信息的深度学习技术。而文献[13]中，作者利用循环神经网络对短期的上下文进行建模，利用门限循环单元对长期的上下文进行建模，将长短期上下文融合到一个深度学习模型中。

与现存方法不同，本文试图利用深度学习技术对地理邻近性进行建模，而非时间、序列等信息。深度学习模型包括许多，如卷积神经网络、循环神经网络、长短期模型和门限循环单元等。但是，上述提到的模型大多是监督学习技术，然而，人类行为具有很大的非监督特性[6]。因此，本文尝试挖掘深度学习技术在非监督领域的优势。换言之，本文利用非监督的深度学习技术(自编码器)对LBSNs中的地理进行建模，挖掘用户的潜在偏好，并最终应用于地点推荐任务。

2 基于地理邻近性的深度自编码器在地点推荐中的应用

2.1 基于TF-IDF的签到数据转换

如前文所述，不同种类中的POI的签到频率不能同等看待，例如休闲场所(酒吧等)，用户的签到频率注定会比较高。因此，本文将用户的签到频率转化为基于类别的偏好数据。

词频-逆向文档频率(Term Frequency-Inverse Document Frequency, TF-IDF)是一种在信息检索中比较流行的加权技术。TF-IDF的初衷是衡量一个词对于一个文档的重要程度，该词的重要程度与它在该文档中出现的次数成正比，同时又与它在语料库中的频率成反比。因此，TF-IDF具有很好的类别区分能力。受此启发，本文将TF-IDF技术用于计算类别在签到频率中的重要程度。

对于一个特定的用户i，对于地点j的签到频率可以进行如下转化：

(1)

其中，xij是用户i对于地点j的签到频次,αij代表模型参数，而βij则代表基于TF-IDF类别的权重：

(2)

其中，Nik代表属于类别k的，且用户i签到的POI数量,集合Cat表示类别集合。Nuser表示用户总数，Nc表示去过类别c所属的地点的用户总数。

2.2 基于地理邻近性的深度自编码器

2.2.1 地理邻近性

许多研究发现，同一个用户签到的POI之间的距离分布服从幂律分布(Power-law Distribution, PD)[7-9，14]，分布函数中的参数可以通过签到数据估计得到，这种地理上的分布也被叫做地理邻近性(Geographical Proximity)。因此，本文利用幂律分布计算POIs之间的地理邻近性：

s=α×Dβ

(3)

其中，α和β代表幂律分布的参数，D代表同一个用户签到的2个POIs之间的距离，而s则表示2个POIs之间的地理邻近性。用户的签到行为受到他们移动性的影响，这种用户移动性可以通过他们签到的POIs的距离分布表示。因此，本文利用基于幂律分布的地理邻近性和签到效用结合描述地理因素对于用户的影响。

2.2.2 深度自编码器

简单的自编码器(Auto-encoder)可以看做是一种3层神经网络[15-16]，分别是输入层、隐藏层和输出层。自编码器的目的是输出数据尽可能还原输入数据，因此，其中输入层到隐藏层之间的过程叫做编码，而隐藏层到输出层之间的过程叫做解码。为了提高自编码器的学习能力，可以将网络扩展到多层，即隐藏层由多层网络构成，由此产生了深度自编码器(Deep Auto-encoder,DAE)[17]。深度自编码器由多层编码网络和多层解码网络组成，其中编码网络将输入数据转换到高层级特征表示，解码网络从高层级特征表示中还原数据。深度网络中，每层特征表示抓取下一层单元之间的强关联。

深度自编码器的学习过程主要分为2个部分：逐层预训练和参数微调。首先逐层、贪婪地进行预训练，之后再利用后向传播算法对网络参数进行最后微调，这样可以避免网络陷入局部最小值。

1)逐层预训练。

本文将深度自编码器中的每一层看做一个受限玻尔兹曼机，之后逐层训练受限玻尔兹曼机。每个受限玻尔兹曼机的输出层作为下一个受限玻尔兹曼机的输入，之后利用对比散度进行训练，这样就形成了一个多层的编码网络。最后将训练后的多层编码网络复制展开成带有相同权重的解码网络，形成深度自编码器，至此，完成深度自编码器的预训练过程。

2)参数微调。

深度自编码器的参数微调过程类似传统神经网络，首先训练数据进入网络，逐层向后传播并计算隐层，利用链式法则对损失函数进行求导，之后将数据的损失值(误差值)逐层向后传播，并逐层更新(微调)网络参数，直至收敛条件，则深度自编码器训练完成。其中后向传播是一种训练神经网络的流行方法，通过数据误差的逐层向后传播，不断更新网络参数。在后向传播阶段，本文采用输入层输出层之间的误差来微调网络权重。具体来说，对于每个训练数据t，集合Lt表示输入层的数据单元集合，由此，本文定义误差函数为总体平方误差：

(4)

其中，yi表示输入层单元i的真实值(输入数据)，oi∈Outputs表示输出层单元i的预测值(模型预测值)。在本文中，对于每个训练实例t,只计算在真实数据集合Lt中的单元，缺失单元不纳入损失函数中。

若训练集T中含有N个训练实例，则总体损失函数可以定义为：

(5)

其中，第一项是所有训练数据损失的平均值，第二项是正则项，用于减小参数量级带来的影响，减缓过拟合问题。

2.2.3 深度自编码器与地理邻近性结合

假设所有的POIs数量是M，用户数量是N，那么在输入层就会有M个单元，代表所有的POIs。同时，每个用户i都存在一个对应的POI集合Li，代表该用户签到过的所有POI，并且集合Li中的所有POI都对应于输入层中的一个单元。假设在深度自编码器中一共存在2R个网络层，即存在R层编码网络和R层解码网络，在每一层中，本文用W(r)和b(r)表示第r层的连接权重和偏置。

然而，每个用户签到的POIs不尽相同，这意味着每个训练实例，都会在输入层存在缺失值。本文中，每个用户i都代表一个不同的自编码器，并且每个自编码器都有不同的输入单元，代表不同的POIs。但是所有的自编码器都共享相应的权重和偏置，在模型训练阶段，POI对应的权重只会通过这些签到过的用户数据进行更新。

正常的DAE在输入输出层之间是没有内部链接的，但是在本文模型中，输入输出层代表POI，而且POI之间存在地理邻近性，因此，DAE输入输出层之间必然存在关联，即应该存在内部链接。由此，本文提出一种基于地理邻近性的DAE模型(Geo-DAE)。在Geo-DAE中，本文在输入输出层之间加入内部链接权重，并且该权重的值等于2个POIs之间的地理邻近性(由公式(3)计算)。另外，该内部权重不参与模型更新，即其值固定不变，只参与模型计算而本身不进行更新。因此，Geo-DAE的模型预训练和学习过程与传统的DAE相似，唯一的不同在于计算输入输出值时，需要考虑内部链接权重。

2.3 产生推荐

本文提出的模型可以输出用户对于所有POI的预测偏好，表示预测的兴趣偏好，将这些偏好的预测值进行排序，之后输出排名靠前的k个候选POI，即可形成推荐。

3 实验及算法评价

3.1 实验数据与评价指标

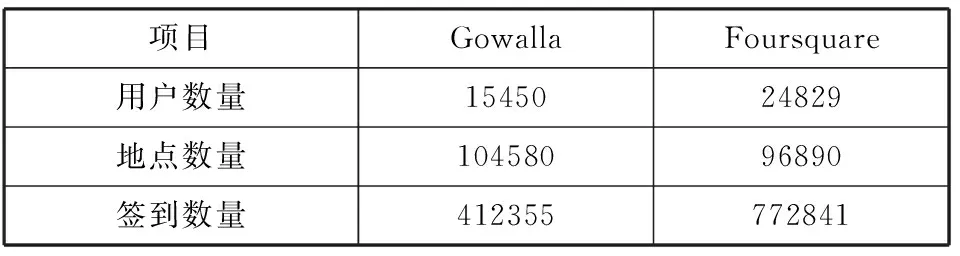
本文实验部分使用了2个真实的LBSNs数据集进行实验：Gowalla数据集和Foursquare数据集。具体信息如表1所示。

表1 Gowalla和Foursquare数据集中的统计数据

项目GowallaFoursquare用户数量1545024829地点数量10458096890签到数量412355772841

为了估计地点推荐系统的质量，实验部分采用如下评价指标：准确率(Precision)、召回率(Recall)和F1。如果给定推荐地点的个数K(K=5,10,15,20,25,30)之后，评价指标可以进行如下定义：

(6)

(7)

(8)

其中，S为测试集中地点集合，L为推荐列表中的地点集合。因此，准确率为推荐列表与测试集重合地点数在推荐列表中的占比，而召回率为所有签到地点中被召回的比重。

3.2 对比算法

本文选择了几个典型的模型作为对比算法，与本文算法进行实验对比。对比算法分别为：融合地理与社交信息的传统协同过滤算法(Geo-CF)[7]、基于地理影响的概率因子模型(Geo-PFM)[5]、基于受限玻尔兹曼机的推荐算法(RBM)[11]。

1)Geo-CF。该方法是传统的基于内存的协同过滤算法，将基于距离的地理邻近性和社交影响融入协同过滤算法之中。

2)Geo-PFM。Geo-PFM是经典的基于模型的协同过滤算法，利用考虑了地理邻近性的隐因子模型处理地点推荐任务。

3)RBM。该方法是基于受限玻尔兹曼机的传统协同过滤推荐算法。

3.3 实验结果分析

本文算法以及其他对比算法在准确率、召回率和F1这3个指标上的实验结果如图1所示。

从图1中可以看出，本文算法Geo-DAE在2个数据集上的表现效果都要高于其他对比算法，具体实验效果排名为：Geo-DAE,Geo-CF,RBM,Geo-PFM。

(a) Gowalla 数据集 (b) Foursquare数据集图1 不同算法的实验对比

本文算法Geo-DAE和协同过滤算法Geo-CF都考虑了地理邻近性，Geo-DAE利用深度自编码器与地理邻近性结合，而Geo-CF则是利用基于朴素贝叶斯的传统协同过滤技术与地理邻近性进行结合。但是Geo-DAE算法实验效果优于Geo-CF，说明深度学习模型对地理邻近性建模更有效，更适合地点推荐场景。深度学习技术可以在多层空间中隐式地学习数据中的潜在特征，因此对地理邻近性也同样具有优势。

本文算法利用Geo-DAE对地理邻近性建模，并且实验效果明显优于RBM，说明Geo-DAE对于地理角度的特征进行了有效的提取，在地点推荐领域具有优势。

另一个基于模型的算法Geo-PFM，在概率矩阵分解模型中加入地理因素，即在矩阵分解算法中加入一项基于距离的参数，来对地理邻近性建模。虽然Geo-PFM同样考虑了地理邻近性，但是本文算法Geo-DAE的实验表现更佳，这意味着本文提出的深度自编码器可以更加有效地对地理邻近性建模，在POI推荐领域Geo-DAE具有很大的潜力。

从图1中可以看出，虽然都考虑了地理邻近性，但是Geo-CF算法明显优于Geo-PFM算法。其中一个原因可能是：虽然Geo-PFM利用复杂的模型对地理邻近性建模，但是简单的朴素贝叶斯方法更适合对地理邻近性建模。在这2种算法中，都利用了与幂律分布相关的函数计算地理邻近性。但是在Geo-PFM算法中，算法首先利用多项式分布为用户计算多个潜在活动区域，在区域内部计算地理邻近性。因此，Geo-PFM效果不佳的另一个原因可能是：整体来讲，用户的移动性(移动距离)服从幂律分布，但是在某个小的区域内可能幂律分布并不能准确地描述用户的移动性，由此导致Geo-PFM的推荐效果不如Geo-CF。因此，虽然地理邻近性有助于提高地点推荐的效果，但如何计算地理邻近性以及有效的建模方式同样至关重要。有效的地理邻近性计算方法和建模方式，更有利于挖掘地理因素对于用户签到行为的影响。

本章利用真实LBSNs中的签到数据，对4种相关的算法进行了实验和分析。通过与3种典型POI推荐算法的分析，证明了本文算法Geo-DAE在多种指标上都具有明显优势。

4 结束语

本文先根据IF-IDF加权理论，将用户签到频率转换成基于类别的偏好数据。之后提出一种基于Geo-DAE的地点推荐算法，充分挖掘POI之间的地理邻近性。最后为了验证本文算法的有效性，利用真实数据进行了实验分析，实验结果证明本文提出的算法相对于对比算法具有明显的优势。

参考文献：

[1] Li Nan, Chen Guanling. Sharing location in online social networks[J]. IEEE Network, 2010,24(5):20-25.

[2] Liang Ting-peng, Lai Hung-Jen, Ku Yi-cheng. Personalized content recommendation and user satisfaction: Theoretical synthesis and empirical findings[J]. Journal of Management Information Systems, 2006,23(3):45-70.

[3] Cheng Chen, Yang Haiqin, King I, et al. A unified point-of-interest recommendation framework in location-based social networks[J]. ACM Transactions on Intelligent Systems and Technology, 2016,8(1): Article No. 10.

[4] 胥皇,於志文,封云,等. 基于LBSN的个性化旅游包推荐系统[J]. 计算机与现代化, 2014(1):186-191.

[5] Liu Bin, Xiong Hui, Papadimitriou S, et al. A general geographical probabilistic factor model for point of interest recommendation[J]. IEEE Transactions on Knowledge and Data Engineering, 2015,27(5):1167-1179.

[6] LeCun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015,521(7553): 436-444.

[7] Ye Mao, Yin Peifeng, Lee W C, et al. Exploiting geographical influence for collaborative point-of-interest recommendation[C]// Proceedings of the 34th International ACM SIGIR Conference on Research and Development in Information Retrieval. 2011:325-334.

[8] Brockmann D, Hufnagel L, Geisel T. The scaling laws of human travel[J]. Nature, 2006,439(7075):462-465.

[9] Gonzalez M C, Hidalgo C A, Barabasi A L. Understanding individual human mobility patterns[J]. Nature, 2008,453(7196):779-782.

[10] Zhang Jia-dong, Chow C Y. CoRe: Exploiting the personalized influence of two-dimensional geographic coordinates for location recommendations[J]. Information Sciences, 2015,293:163-181.

[11] Salakhutdinov R, Mnih A, Hinton G. Restricted Boltzmann machines for collaborative filtering[C]// Proceedings of the 24th International Conference on Machine Learning. 2007:791-798.

[12] Zhou Ningnan, Zhao W X, Zhang Xiao, et al. A general multi-context embedding model for mining human trajectory data[J]. IEEE Transactions on Knowledge and Data Engineering, 2016,28(8):1945-1958.

[13] Song Xuan, Zhang Quanshi, Sekimoto Y, et al. Prediction and simulation of human mobility following natural disasters[J]. ACM Transactions on Intelligent Systems and Technology, 2017,8(2): Article No. 29.

[14] Miller H J. Tobler’s first law and spatial analysis[J]. Annals of the Association of American Geographers, 2004,94(2):284-289.

[15] Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006,313(5786):504-507.

[16] 牛玉虎. 卷积稀疏自编码神经网络[J]. 计算机与现代化, 2017(2):22-29.

[17] 曲建岭,杜辰飞,邸亚洲,等. 深度自动编码器的研究与展望[J]. 计算机与现代化, 2014(8):128-134.