基于粒子群投影寻踪插值模型的土壤质量评价
, ,
(新疆大学 信息科学与工程学院, 新疆 乌鲁木齐 830046)
1 材料与方法
1.1 评价等级标准的建立方法
土壤质量评价的框架体系要确保全面性。影响土壤质量的因素很多,选取的指标应能正确反映土壤基本功能,又能避免使指标体系过于复杂化[2]。土壤质量评价体系目前没有明确标准,根据全国第2次土壤普查质量评价指标体系,本文中选取8个代表性的分析性定量指标,即有机质、全氮、全磷、全钾、速效氮、速效磷、速效钾、pH。各个因素的指标评价标准如表1所示。
1.2 建立模型
针对非线性、 非正态高维观测数据(生物学指标、 化学指标等)难以计算处理的情况,采用投影寻踪(projection pursuit)方法将数据投影到低维子空间对投影值进行统计分析,获得高维数据的结构特征[7-8]。在土壤数据的分析过程中,确定最佳投影方向是解决评价问题的关键点,传统的优化方法对于计算特定目标函数具有一定的优势,本文中构建的投影寻踪插值模型基于粒子群算法[9],可以有效地克服传统方法的局限性,具体步骤如下。

表1 土壤质量等级评价标准
1.2.1 建立样本集
设由评价标准表产生的样本经验等级为y(i),样本指标表示为{x*(i,j)|i=1, 2, …,n;j=1, 2, …,p},其中n为样本个数,p为指标个数,1~N表示等级由低到高。先对各指标值无量纲化处理,统一变化范围,加快训练的收敛性,然后进行归一化处理。
对于正向指标,
(1)
对于逆向指标,
(2)
式中:xmax(j)、xmin(j)表示第j个指标值的2个极值;x(i,j)为指标特征值归一化的序列[10]。
式(1)、(2)应用于正向指标(权重大于0)和逆向指标(权重小于0)的归一化处理,但对于不能明确判定指标特征的,则采用式(1)进行归一化处理。
1.2.2 投影值的计算
设a=(a1,a2, …,ap)为投影方向, 将数据x(i,j)投影到a上,得到投影值z(i),

(3)
由式(3)可见,选定最优投影方向后,z(i)的值越大,数据{x(i,j)}中的信息提取得越多。
1.2.3 构造投影指标函数Q(a)
构造投影指标函数
Q(a)=Sz|Rzy|,
(4)
式中:Sz为投影值z(i)的标准差;Rzy为z(i)与y(i)的相关系数。
(5)
(6)
式中E(z)、E(y)分别为序列{z(i)}和{y(i)}的均值。
式(5)中Sz越大,获得{x(i,j)}的变异信息越多;式(6)中|Rzy|越大,投影值就可以反映预测因子系统更多的变异信息,对预测对象y(i)的解释性越好。
数据结构的不同特征可以通过不同的投影方向反映,能够表现出高维数据某类特征结构的就是最佳投影方向,最佳投影方向预测就是投影指标函数的最大化问题[11],即
maxQ(a)=Sz|Rzy|,
(7)
(8)
a=(a1,a2,…,ap)为优化变量的非线性优化问题,本文中采用罚函数法[12]生成新的目标函数,将有约束优化问题转化为无约束优化问题,即
(9)
式中h为惩罚因子。
1.2.4 投影指标函数优化算法
粒子群算法通过不断迭代计算,将每个粒子与其个体历史最优位置和在粒子群中的全局最优位置比较,从而不断调整自身位置来接近最优位置,所有粒子的最终聚集位置就是优化问题的解。
投影寻踪模型中的投影方向即为粒子群算法要优化的问题[13]。设粒子的种群规模为N,第k(k=1,2,…,N)个粒子的速度和位置更新公式为
vk(t+1)=wvk(t)+c1r[qk(t)-ak(t)]+
c2r[g(t)-ak(t)],
(10)
ak(t+1)=ak(t)+vk(t+1),
(11)
式中:w为惯性权重因子;c1、c2为常数,称为学习因子;r是介于[0,1]随机数;q是历史最优位置;g是全局最优位置,迭代次数达到预定值,就可通过粒子聚集的位置获得最佳投影方向a*。
1.2.5 投影寻踪插值模型
将计算出的最佳投影方向a*代入式(3)获得投影值z*(i),根据z*(i)-y(i)的散点图建立土壤等级评价模型y*=f(z),代入归一化处理后的评价样本得出各评价样本的所属等级。
2 结果与分析
选取全国第2次土壤普查中的黑龙江省、长白山、内蒙古自治区及新疆维吾尔自治区阜康市共4个地区剖面取样的4组实测数据作为待评价的样本,见表2。
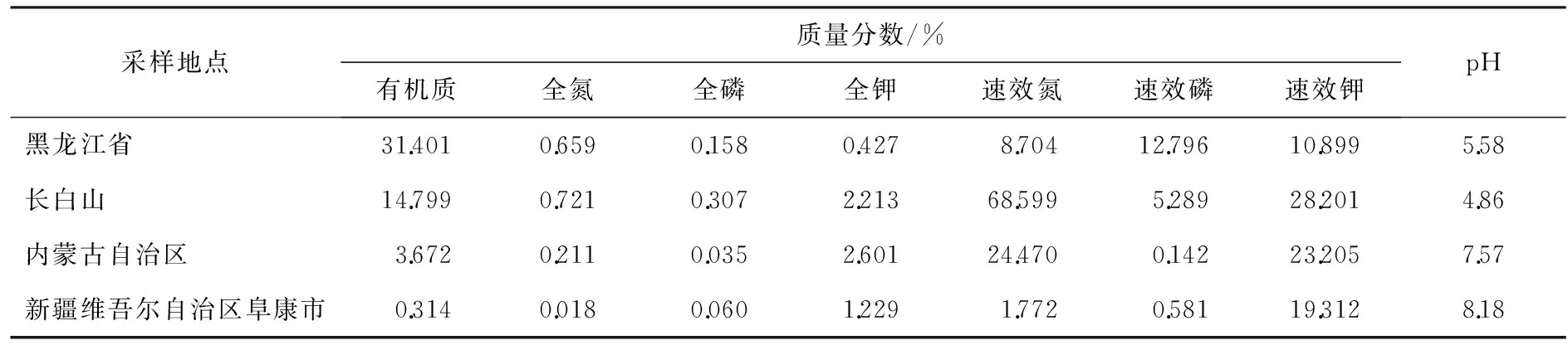
表2 待评测样本数据表
按照表1所示的6个土壤质量评价等级范围,从全国第2次土壤普查数据中每个等级均匀随机产生100个指标, 形成600个样本数据x*(i,j), 并对x*(i,j)进行归一化处理为x(i,j),i=1, 2,…,600,y=1,2,…,8。参数设置为:N=100,c1=c2=2,h=200。 MATLAB程序计算出最大投影指标值为0.729 7, 最佳投影方向a*=(0.230 9, 0.211 3, 0.312 1, 0.278 0, 0.431 3, 0.500 2, 0.446 3, 0.305 8),具体结果见图1。
最佳投影方向各分量绝对值越大,对质量评价影响就越大,该数据还可以作为检验土壤质量分级标准合理性的依据。将a*代入式(3)可以计算出最佳投影值,最佳投影值与对应等级如图2所示。


图1 最佳投影方向a*

图2 z*(i)与y(i)的散点关系图

表3 土壤质量等级评价结果
3 结论
本文中依据全国第2次土壤普查质量评价等级标准构建评价指标样本,把样本数据应用于粒子群投影寻踪插值模型中,获得多维土壤质量评价指标的最佳投影值, 根据最佳投影值与质量等级的对应关系建立插值模型以实现对土壤质量等级的综合评价。模型建立和评价的方法切实可行,评价结果科学合理,避免了人为干扰,为土壤质量评价等方面的研究提供了一个新思路。
参考文献:
[1] 路鹏, 苏以荣, 牛铮, 等. 土壤质量评价指标及其时空变异[J]. 中国生态农业学报, 2007, 15(4):190-194.
[2] 黄勇, 杨忠芳. 土壤质量评价国外研究进展[J]. 地质通报, 2009, 28(1): 130-136.
[3] 吴玉红, 李云,郝兴顺,等. 土壤质量评价国内外研究进展[J]. 安徽农学通报, 2012, 18(16):24-25.
[4] 黄鑫,李洪良,邱林. 土壤质量等级模糊模式识别综合评价研究[J]. 人民黄河,2012,34(3):68-70.
[5] 刘占锋, 傅伯杰, 刘国华, 等. 土壤质量与土壤质量指标及其评价[J]. 生态学报, 2013, 26(3): 901-913.
[6] 张鑫, 余树全, 李清林, 等. 洞头列岛土地利用对土壤及沉积物重金属污染的影响及其生态风险评价[J]. 生态科学, 2016, 35(5):126-135.
[7] ZHANG H L, WANG C, FAN W H. A projection pursuit dynamic cluster model based on a memetic algorithm[J]. Tsinghua Science and Technology, 2015, 20(6): 661-671.
[8] 韩锐, 董增川, 施露, 等. 投影寻踪法在滦河流域生态系统健康评价中的应用[J]. 水力发电,2016,42(9):5-8.
[9] LIU Y L, LIU D F, LIU Y F, et al. Rural land use spatial allocation in the semiarid loess hilly area in China: using a particle swarm optimization model equipped with multi-objective optimization techniques[J]. Science China Earth Sciences, 2012, 55(7): 1166-1177.
[10] 陈默. 基于投影寻踪等级评价模型的大伙房水库水质评价[J]. 甘肃水利水电技术, 2016, 52(12):1-3.
[11] 李芳凤, 张国权. 粒子群投影寻踪模型在土壤重金属监测中的应用[J]. 广东农业科学, 2012, 39(8):68-70.
[12] 李志刚, 吴文传, 张伯明, 等. 一种基于高斯罚函数的大规模无功优化离散变量处理方法[J]. 中国电机工程学报, 2013, 33(4): 68-76
[13] 赵小勇, 付强, 邢贞相. 投影寻踪等级评价模型在土壤质量变化综合评价中的应用[J]. 土壤学报,2007,44(1):164-168.

