单层网络目标控制的多属性决策方法*

杜亚星，鲁富荣，仇智鹏，钱宇华+

1.山西大学 大数据科学与产业研究院，太原 030006

2.山西大学 计算智能与中文信息处理教育部重点实验室，太原 030006

3.山西大学 计算机与信息技术学院，太原 030006

1 引言

控制复杂系统是人们对复杂系统模型结构及相关动力学进行研究的最终目标，具有广泛的应用价值，例如控制网络上的同步、控制疾病和谣言的传播等，引起众多学者的广泛关注。Liu等人[1]基于结构可控理论[2]，首次提出了控制复杂网络系统的方法，并且取得了很多重要的研究成果。然而在实际中，通常缺乏有效的技术和工具来实现复杂网络的有效控制[3-8]。

通过结构可控性理论和最大匹配方法[9-10]，人们能够确定控制一个网络所需的最小的驱动节点数目[11]。对于工程系统，如自动驾驶飞机系统，结构控制是至关重要的。然而，许多生物、技术和社会系统是巨大的和复杂的[12]，对它们实现结构控制既不可行，也不必要。因此，在一个选定的任务中控制一个系统的目标节点是至关重要的。在生物、化学工程[13]、传播学[14]和经济网络[15]确定一组最小的驱动节点方法满足任意的目标控制复杂的网络，仍然是一个悬而未决的问题[16]。

由于现有的复杂网络节点重要性的单一评价指标存在局限性，并且节点在复杂网络中的重要性不仅仅受单一因素的影响，可以采用一种基于多属性决策的节点重要性综合评价方法[17]。运用此方法可以有效地找出整个网络中比较重要的节点，对其进行目标控制，其所需的驱动节点数目在很大程度上比单一指标所需的数目少。

2 目标控制理论

与结构控制理论不同，目标控制不会对整个网络的所有节点加以控制，而是旨在选择并控制网络中的部分节点。本文将主要研究线性时不变系统的目标控制[18]。对于以下一个线性时不变系统：

其中，x∈RM，u∈RM和y∈RS分别代表系统的初始状态、输入和输出向量。A∈RN×N,B∈RN×M和C∈RS×N分别代表系统的状态、输入和输出矩阵。A是网络系统的邻接矩阵，B代表输入外部信号后哪些节点被控制，u是对矩阵B施加的独立不相干的控制输入，C是需要控制的目标节点的输出矩阵。

给定一个特定的网络N={1,2,…N},θ={c1,c2,…,cs}为所需要控制的目标节点集，其中S=|C|=fN。C=[I(c1),I(c2),…,I(cs)]表示输出矩阵，其中I(ci)表示一个N×N单位矩阵的第I行。系统(A,B,C)是否可控定义如下：对于一个给定的目标节点集，如果存在相互独立的输入向量u(t)=(u1(t),u2(t),…,uM(t))Τ，能够使得驱动节点在有限的时间间隔内从任意的初始状态到达任意想要的最终状态。

系统(A,B,C)是可控的当且仅当输出可控子集的维度满足：

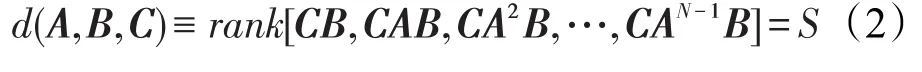
以上给出了目标可控的数学条件。如果S=N，C是单位矩阵，式（2）和结构控制一样满足Kalman可控条件[18]。

3 节点重要性

重要节点是指相比网络其他节点而言，能够在更大程度上影响网络结构与功能的一些特殊节点。重要节点一般数量非常少，但其影响却可以快速地波及到网络中大部分节点[19]。例如，在对一个无标度网络的蓄意攻击中，少量最重要节点被攻击就会导致整个网络瓦解[20]；微博中最有影响力的几个用户所发的微博很快就能传遍整个网络[21]；仅仅1%的公司却控制着40%的全球经济。可见重要节点对网络的结构和功能有着巨大的影响。因此，在一个网络中选出重要的节点并对它们进行目标控制意义重大[22]。

3.1 单一评价指标

目前，学术界已经提出很多衡量节点重要性的单一评价指标。然而，在复杂网络中，仅仅依赖于单一指标来判断节点在网络中的重要程度具有很大的片面性[17]。需要从不同的角度，利用节点的多个重要性指标来进行综合评价。

进行综合评价时，首先要对可用的评价指标进行筛选。本文基于“逼近理想排序法”[23]的多属性决策方法，对网络中单个节点的度中心性、介数中心性、接近中心性、PageRank[24-25]这4个指标作为决策评价方案的属性进行综合计算。度中心性对于有向网络来说，每个节点的度分为出度和入度，这里仅对入度中心性进行分析，也就是说，只考虑进入一个节点的流通量以及它的接收信息的能力；对于介数中心性和接近中心性，其基础思想都是按照最短路径定义的，最短路径算法对有向网络是适用的，因此可以对其进行相应的修改使其适用于有向网络；Page-Rank本身就可以对有向网络进行计算。

（1）入度中心性（degree centrality）

节点i的度ki定义为与该节点连接的其他节点的数目。入度中心性定义为节点i的入度与该节点可能存在的最大边数的比率。入度中心性可由式（3）计算：

其中，N为节点数量；表示网络中进入节点i的边数。入度中心性定义表明了一个节点接收其他节点信息通信的能力，数值越大，在网络中越重要。

（2）介数中心性（betweenness centrality）

节点i的介数定义为网络中节点对j与k之间最短路径经过节点i的条数占所有最短路径数的比例。若gjk(i)表示节点对j与k之间经过节点i的条数，njk表示节点对j与k之间存在的所有最短路径的条数，则介数中心性可表示为：

介数中心性的值越大，表示该节点在网络中的影响力越大。

（3）接近中心性（closeness centrality）

节点i的接近中心性定义为其到网络中其他所有节点距离之和的倒数。实际网络并不都是完全连通的，将接近中心性用以下公式表示，同样适合不连通复杂网络的情形，其表达式为：

如果节点vi和vj之间没有路径可达，则定义dij=∞，即1/dij=0。N为节点数量，dij表示以节点i为起点，以j为终点的最短路径中所含边的数量[25]。接近中心性越大，表示节点越居于复杂网络的中心位置。

（4）PageRank

PageRank算法认为万维网中一个页面的重要性取决于指向它的其他页面的数量和质量。初始时刻，赋予每个节点（网页）相同的PR值，然后进行迭代，每一步把每个节点当前的PR值平分给它所指向的所有节点。修正的PageRank算法在上述过程基础上引入一个随机跳转概率c。每一步，不管一个节点是否为悬挂节点（出度为0的节点），其PR值都将以c的概率均分给网络中所有节点，以1-c的概率均分给它指向的节点。每个节点更新后的PR值为它所获得的PR值之和，因此节点vi在t时刻的PR值为：

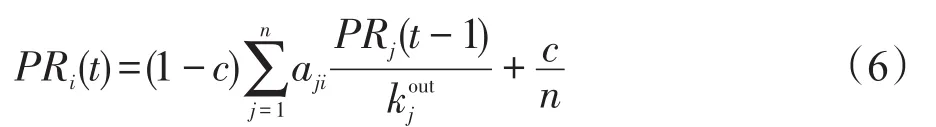
其中，kojut为节点vj的出度。针对万维网的网页排序，研究显示c=0.15是一个比较好的参数。节点的PR值越大，表示节点越重要。

基于以上4个指标，本文将建立一种基于多属性决策的节点重要性评价方法。

3.2 综合评价体系

基于多属性决策的节点重要性综合评价方法，其基本思想是将复杂网络中的每一个节点看作一个方案，将评价节点重要性的多个评价指标分别看作各方案的属性，从而将节点重要性的评价问题转化为一个多属性决策问题，决策的准则是评价各方案在复杂网络中的重要程度。

假设复杂网络中有N个节点，用集合P={P1,P2,…,PN}表示，每个节点特性指标有M个，用集合Q={Q1,Q2,…,QM}来表示，则此网络中的第i个节点的第j个指标可用Pi(Qj)(i=1,2,…,N;j=1,2,…,M)来表示，则节点的多属性（指标）矩阵可表示为:

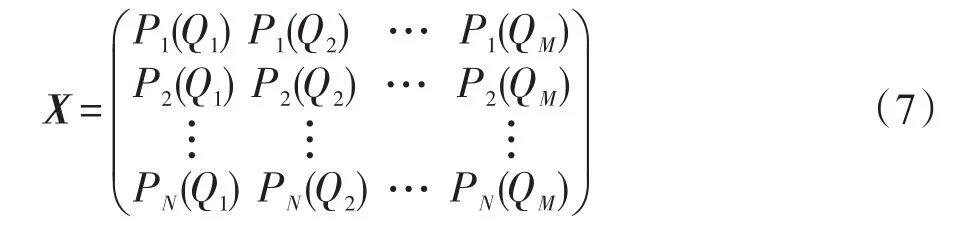
上述所选指标（入度中心性DC、介数中心性BC、接近中心性CC和PageRankPR）均为效益型指标，即值越大表示该节点越重要，因此需要对矩阵X做归一化，得到R=(rij)N×M，其中：

根据层次分析法（analytic hierarchy process，AHP）[26]，并经过一致性经验，为节点重要性多属性评价模型的各个指标赋予权重：首先经过比较计算建立一个比较矩阵B；然后通过变换将比较矩阵转化为判断矩阵，并进行一致性检验；最后得到指标权重。参照文献[15]对比较矩阵的值做了调整，见表1。

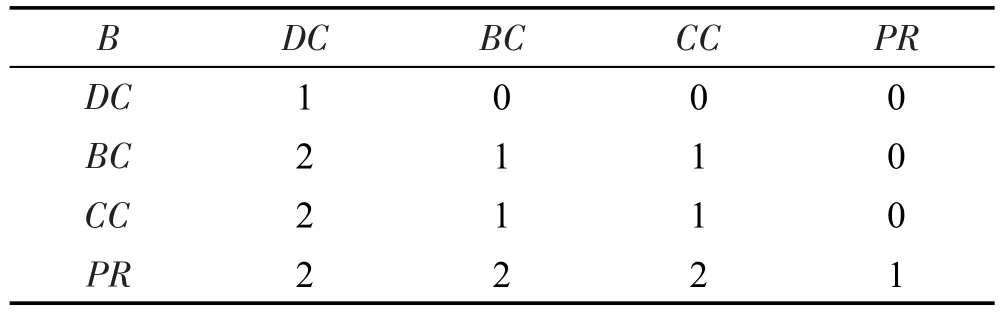
Table 1 Value of comparison matrix表1 比较矩阵的值

表1中：

对比较矩阵B的构建基于以下因素考虑：因为度中心性在有向网络中涉及的网络结构因素最少，所以和其他指标相比重要性较差；介数中心性和接近中心性均基于最短路径理论，很难对比两个指标的好坏，在矩阵B中给出了重要性相同的评价；Page-Rank和其他3个指标相比，针对有向网络可以准确地找出网络中相对重要的节点，因此本文在比较矩阵B的构造中给PageRank赋予了比其他指标更高的值。

对比较矩阵B按照极差法构造判断矩阵[26]，经一致性检验，得到各相关指标权重的值分别为wDC=0.086 1,wBC=0.207 3,wCC=0.207 3,wPR=0.499 3。

设第j个指标的权重为wj(j=1,2,…,m,∑wj=1)，该向量和规范化决策矩阵R构成加权规范化矩阵：

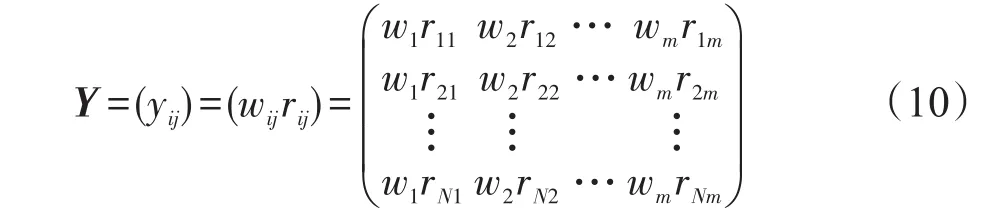
采用理想方案[23]对每个节点的重要性进行评估，计算公式如下：

其中，与可通过欧式范数计算得到：=为矩阵Y每列中的最大值，yminj为矩阵Y每列中的最小值。

计算理想方案的值Ki，按照Ki值的大小进行重要度排序，完成评估任务。经过上述处理，Ki值越大表示节点在网络中的重要程度越高。

4 实验分析

4.1 在真实网络上的实验分析

基于以上理论，对不同类型的真实数据分别按DC、BC、CC、PR和综合指标对节点的重要性进行计算排序，从大到小选取前10%的节点，把它们当作目标节点分别进行控制，用目标控制算法在整个网络中控制这些目标节点，然后分析驱动节点的数量。结果如表2所示，其中黑色加粗下划线数字表示效果差的方法所需要的驱动节点数目。

表2中Type为数据类型，Name为数据名称，N和L是节点和边的数量，ND是控制整个网络所需要的驱动节点数目，这个结果和结构可控理论运用最大匹配算法得出的结果一致；n为分别对各个数据选取10%节点的数目（即各个数据在整个网络中需要控制的目标节点数目）；DC、BC、CC、PR和AD是按各自的指标值进行排序选取前10%的节点作为目标节点进行控制时得出的驱动节点的数目（AD为综合指标下计算得出的驱动节点数目）。从表2中可以看出，对于大部分数据来说，综合性指标比其他单一指标得出的驱动节点的数量都少。

Table 2 Driver nodes based on single index and integrated index表2 基于单一指标及综合指标所得到的驱动节点数

可以看出，各个数据在综合性指标下计算得出的驱动节点数目大部分都比单一指标低。虽然有个别指标，例如介数中心性BC对于数据WikiVote比综合性指标低，但是对于其他数据，驱动节点数目的结果并不是很理想。其他指标如入度中心性DC、接近中心性CC以及PageRank值PR等单一指标的结果均类似这种情况，对于大部分数据来说综合指标情况下驱动节点数量均相对较少。因此在综合性指标能够有效地选取出网络中重要节点的基础上，达到了整体而言驱动节点数目相对最少。

4.2 在人工生成网络上的实验分析

为了研究平均度＜k＞和幂律γ对驱动节点数目的影响，将4.1节的分析过程运用到无标度网络和ER随机模型网络中。

图1是无标度网络的处理结果，纵坐标均是控制模型网络所需驱动节点数量与网络目标节点数量的比值。图1中横坐标＜k＞和γ分别代表平均度和幂律，纵坐标ratio代表驱动节点与目标节点的比率。图（a）和（c）为基于结构控制理论即控制整个网络（10 000个节点）的结果，图（b）和（d）是基于目标控制理论对网络选取的10%重要节点（1 000个节点）进行目标控制的结果。所有实验结果都是重复做了10次取平均值。

图2是ER随机网络的处理结果，纵坐标依旧是控制模型网络所需驱动节点数量与网络目标节点数量的比值。横坐标＜k＞代表平均度，纵坐标ratio代表驱动节点与目标节点的比率。图（a）为基于结构控制理论即控制整个ER网络（10 000个节点）的结果，图（b）则是基于目标控制理论对网络选取的10%重要节点（1 000个节点）进行目标控制的结果。所有实验结果都是重复做了10次取平均值。

图1（a）说明，网络幂律γ一定时，随着网络平均度＜k＞的增大，结构控制时驱动节点与网络节点的比值逐步降低，即所需驱动节点的数量在减少；网络平均度＜k＞一定时，幂律γ越大，比值越小，驱动节点的数量越小。

Fig.1 Scale-free network processing results图1 无标度网络的处理结果

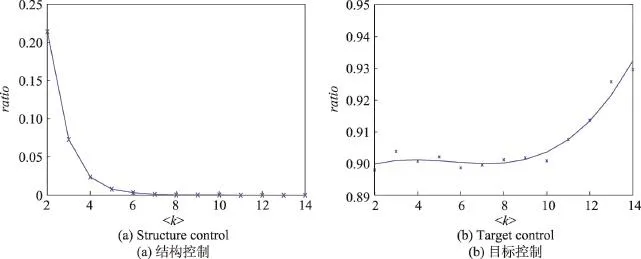
Fig.2 ER network processing results图2 ER随机网络的处理结果

图1 （b）说明，网络幂律γ一定时，随着＜k＞增大，目标控制时驱动节点与目标节点的比值整体先下降后上升；对于不同的幂律值又有不同的变化，γ=2.4时，曲线先上凸后下凹；而γ=5.0时，曲线先下凹后上凸。

图1（c）表明，网络平均度＜k＞一定时，随着幂律γ增大，结构控制时驱动节点与网络节点的比值逐步降低，所需驱动节点的数量减少；幂律值γ一定时，平均度＜k＞越大，比值越小，驱动节点的数量反而越小。

图1（d）表明，平均度 ＜k＞=5时，随着幂律γ增大，目标控制时驱动节点与目标节点的比值曲线先下凹后上凸，当＜k＞逐渐增大，所需驱动节点的数量逐渐上升，并且驱动节点与目标节点的比值逐渐趋于1，当＜k＞=16时，比值几乎完全为1。可以得出，当网络异常稠密时，目标控制所需驱动节点数目即为目标节点的数目；当网络幂律γ一定时，随着平均度＜k＞的增大，目标控制时驱动节点与目标节点的比值增加，所需驱动节点数量增加。

对于图1（d），正是由于只选取了10%的目标节点（其选取数量为1 000），驱动节点数量大部分密集在950～1 000之内，从而驱动节点与目标节点比例也集中在[0.95,1.00]区间内，则纵坐标值很接近，导致个别数据波动时被放大，实际曲线变化的趋势为开始时下降，然后逐渐上升，整体趋势是很明显的。

由图2（a）可以看出，随着网络平均度的增大，通过结构匹配算法控制整个网络所需驱动节点减少；从图2（b）看出，随着网络平均度的增大，目标控制时所需驱动节点增加。由此可以得出，对于越稠密的ER随机网络，目标控制时所需的驱动节点越多。

5 结束语

本文在目标控制中提出一种基于多属性决策的节点重要性综合评价方法，以此来选取重要的节点进行目标控制。在真实网络与人工生成网络上进行实验，通过综合性指标选取10%的节点。结果表明，在真实网络上，通过综合性指标得出的驱动节点数量明显整体比单一指标少；在人工生成网络上，无论对于无标度网络还是ER随机网络，驱动节点与目标节点数量的比值曲线整体的趋势是一个上升的过程。此外，对于上述两种网络，平均度越大，即当网络越稠密时，目标控制所选出的重要节点需要的驱动节点越多。

[1]Liu Yangyu,Slotine J J,BarabásiAL.Controllability of complex networks[J].Nature,2011,473(7346):167-173.

[2]Lin C T.Structural controllability[J].IEEE Transactions on Automatic Control,1974,19(3):201-208.

[3]Yuan Zhengzhong,Zhao Chen,Di Zengru,et al.Exact controllability of complex networks[J].Nature Communications 2013,4:2447.

[4]Gong De'en.An introduction to the economic cybernetics[M].Beijing:China Renmin University Press,1988.

[5]Zheng Dazhong.Linear system theory[M].Beijing:Tsinghua University Press,1990.

[6]Guan Zhizhong,Xia Gongke,Meng Qiao.Signal and linear system[M].Beijing:People's Education Press,1982.

[7]Rugh W J.Linear system theory[M].Upper Saddle River:Prentice-Hall,1996.

[8]Chen C T.Linear system theory and design[M].Oxford:Oxford University Press,1995.

[9]Lovasz L.Matching theory(North-Holland mathematics studies)[M].Oxford:Elsevier Science Ltd,1986.

[10]Hopcroft J E,Karp R M.Ann5/2algorithm for maximum matchings in bipartite graphs[J].SIAM Journal on Computing,1973,2(4):225-231.

[11]Kuchtey J,Fulton S A,Reba S M,et al.Interferon-αβ mediates partial control of early pulmonary mycobacterium bovis,bacillus Calmette-Guérin infection[J].Immunology,2006,118(1):39-49.

[12]Kalman R E.Mathematical description of linear dynamical systems[J].Journal of the Society for Industrial&Applied Mathematics,1963,1(2):152-192.

[13]Baldea M,Daoutidis P.Model reduction and control of reactorheat exchanger networks[J].Journal of Process Control,2006,16(3):265-274.

[14]Cohen R,Havlin S,Ben-Avraham D.Efficient immunization strategies for computer networks and populations[J].Physical Review Letters,2004,91(24):247901.

[15]Galbiati M,Delpini D，Battiston S.The power to control[J].Nature Physics,2013,9(3):126-128.

[16]Xie Guangming,Wang Long.Controllability and stabilizability of switched linear-systems[J].Systems&Control Letters,2003,48(2):135-155.

[17]Yu Hui,Liu Zun,Li Yongjun.Key nodes in complex networks identified by multi-attribute decision-making method[J].Acta Physica Sinica,2013,62(2):020204.

[18]Gao Jianxi,Liu Yangyu,D'Souza R M,et al.Target control of complex networks[J].Nature Communications,2014,5:5415.

[19]Albert R,Jeong H,Barabási A L.Error and attack tolerance of complex networks[J].Nature,2000,406:378-382.

[20]Cohen R,Erez K,Ben-Avraham D,et al.Breakdown of the Internet under intentional attack[J].Physical Review Letters,2001,86(16):3682.

[21]Weng Jianshu,Lim E P,Jiang Jing,et al.Twitterrank:finding topic-sensitive influential Twitterers[C]//Proceedings of the 3rd International Conference on Web Search and Web Data Mining,New York,Feb 4-6,2010.New York:ACM,2010:261-270.

[22]Hou Lvlin,Lao Songyang,Xiao Yandong,et al.Recent progress in controllability of complex network[J].Acta Physica Sinica,2015,64(18):477-487.

[23]Dedania H V,Shah V R,Sanghvi R C.Portfolio management:stock ranking by multiple attribute decision making methods[J].Technology&Investment,2015,6(4):141-150.[24]Qin Li,Yang Zilong,Huang Shuguang.Synthesis evaluation method for node importance in complex networks[J].Computer Science,2015,42(2):60-64.

[25]Ren Xiaolong,Lv Linyuan.Review of ranking nodes in complex networks[J].Chinese Science Bulletin,2014,13:1175-1197.

[26]Zhu Yin,Meng Zhiyong,Kan Shuyu.Determination of weight value by AHP[J].Journal of Northern Jiaotong University,1999,23(5):119-122.

附中文参考文献：

[4]龚德恩.经济控制论概论[M].北京:中国人民大学出版社,1988.

[5]郑大钟.线性系统理论[M].北京:清华大学出版社,1990.

[6]管致中,夏恭恪,孟桥.信号与线性系统[M].北京:人民教育出版社,1982.

[17]于会,刘尊,李勇军.基于多属性决策的复杂网络节点重要性综合评价方法[J].物理学报,2013,62(2):020204.

[22]侯绿林,老松杨,肖延东,等.复杂网络可控性研究现状综述[J].物理学报,2015,64(18):477-487.

[24]秦李,杨子龙,黄曙光.复杂网络的节点重要性综合评价[J].计算机科学,2015,42(2):60-64.

[25]任晓龙,吕琳媛.网络重要节点排序方法综述[J].科学通报,2014(13):1175-1197.

[26]朱茵,孟志勇,阚叔愚.用层次分析法计算权重[J].北京交通大学学报,1999,23(5):119-122.