多重代价多粒度决策粗糙集模型研究*

陈家俊，徐华丽，魏 赟

1.皖西学院 电子与信息工程学院，安徽 六安 237012

2.同济大学 电子与信息工程学院，上海 201804

3.嵌入式系统与服务计算教育部重点实验室（同济大学），上海 201804

4.兰州交通大学 铁道技术学院，兰州 730000

1 引言

粗糙集理论[1-2]是波兰数学家Pawlak提出的一种处理不确定、不精确信息系统的新型数学工具，决策粗糙集模型[3]是针对经典粗糙集模型在处理分类决策时缺乏容错能力和风险代价敏感性等问题提出的一种概率型粗糙集拓展模型，是粗糙集理论的重要组成部分，近年来备受广大学者关注。

对决策粗糙集的研究主要体现在两方面：一方面为决策粗糙集模型及其拓展模型的研究，如基于风险代价的决策粗糙集模型[4-6]、多用户决策粗糙集模型[7]、三支决策和决策粗糙集融合模型[8]等。在决策粗糙集模型研究中，阈值的确定问题是其关键因素之一，其中基于代价损失的阈值求解方法得到广泛关注。姚一豫等人[3,9]根据贝叶斯最小风险决策理论，详细分析了基于代价损失函数的阈值求解方法。决策粗糙集模型是基于单个代价损失矩阵构建的，因此获得的决策规则及决策代价存在局限性；文献[4-6]从多代价损失角度出发，提出了多代价决策粗糙集概念，并研究了悲观决策粗糙集和乐观决策粗糙集模型。而实际生活中专家给定的代价损失矩阵主观性较强，且每个专家在领域的认可度差别较大，通过研究乐观和悲观代价决策粗糙集模型仅能预测最小和最大决策代价，不能满足人们往往更希望获得具有代表性的决策代价的需求。对决策粗糙集的另一研究主要体现在决策粗糙集的属性约简、决策分类和规则获取方法方面，其中决策粗糙集模型的相关性质和属性约简算法是重要的研究内容。文献[10-14]分别从不同的角度研究了决策粗糙集属性约简方法。以上无论对决策粗糙集模型还是对决策粗糙集知识获取方法的研究，都是建立在单一不可分辨关系基础上，而在实际决策问题分析中，往往需要从多粒度、多层次角度对目标概念进行分析和处理。Qian等人[15]首先将多粒度概念融入到粗糙集模型中，提出了多粒度粗糙集模型，在此基础上，学者们纷纷提出了各种基于多粒度粗糙集模型的扩展模型和相关算法[16-20]。而现有的多粒度粗糙集模型大都集中在以经典粗糙集和变精度粗糙集模型为基础的，对于多粒度决策粗糙集模型的研究较少。自2014年Qian等人[21]首先提出多粒度决策粗糙集模型基本框架以来，近两年对多粒度决策粗糙集模型的研究屈指可数[22-25]，其中文献[22]分析了不完备多粒度决策粗糙集模型，文献[24]提出了基于覆盖的多粒度决策粗糙集模型。而这些文献仅针对多粒度决策粗糙集模型的构建以及模型所具有的相关性质进行研究，对多粒度决策粗糙集模型中决策代价和多粒度在决策粗糙集模型中的应用并没有进行深入的研究。

本文在对基于多重代价决策粗糙集模型和多粒度粗糙集模型的研究基础上，为克服基于单代价损失矩阵构建的模型存在的局限性，综合考虑多重代价矩阵和多粒度思想，将权重均值代价策略引入决策粗糙集中，提出了一种权重多重代价的不完备多粒度决策粗糙集模型。在不完备信息系统中，分析了悲观代价决策粗糙集、乐观代价决策粗糙集和权重多重代价多粒度决策粗糙集模型，并给出了各决策代价的总代价计算公式。最后以权重多重代价的多粒度决策粗糙集模型为例，讨论了该模型下随着粒度的变化其正域的变化情况，并给出了一种基于代价最小化的粒度约简方法。

2 预备知识

2.1 不完备信息系统与容差关系

若四元组S=(U,A,V,f)是一个信息系统，S包含一组非空的有限对象集合，U={x1,x2,…,xn}为论域；A=C∪D(C∩D=∅)表示属性的有限集合，C表示条件属性集合，D表示决策属性集合；，其中Va表示属性a的值域；F为U×A→V的一个信息函数，表示为f(x,α)∈Va,∀α∈A,x∈U；假设C包含m个条件属性，用C={c1,c2,…,cm}表示，若存在任意ci∈C，x∈U，有f(x,ci)=*（*表示未知属性值），则称该信息系统为不完备决策信息系统。

若决策表S=(U,C∪D,V,f)为一个不完备决策信息系统，对于任意子集P⊆C，由P决定的U上的容差关系TP定义为TP={(x,y)∈U×U|∀a∈P,f(x,a)=f(y,a)⋁f(x,a)=*⋁f(y,a)=*}。显然TP满足自反性和对称性，而不一定满足传递性。对于∀x∈U,TP(x)={y∈U|(x,y)∈TP}称为x的P容差类，TP(x)描述了与对象x在属性集合P下的最大不可区分对象子集。对于任意子集X⊆U，则在属性集P下X关于容差关系的下近似集和上近似集分别定义为:

2.2 决策粗糙集

若S=(U,C∪D,V,f)为一个不完备决策信息系统，假设Ω={θ1,θ2,…,θm}表示对象的m个状态集，B={b1,b2,…,bt}表示t个可能的决策，对于任意x∈U，令Pr(θj|x)表示对象x具有状态θj的条件概率，λ(bi|x)表示对象x在状态θj下采取决策bi的风险代价，则根据贝叶斯风险决策规则，对象x采取决策bi的期望风险可表示为：

根据Yao提出的决策理论粗糙集，设Ω={X,XL}表示对象的两种状态集，每种状态对应3种决策动作，记为B={αP,αN,αB}，其中αP、αN、αB分别表示将对象x进行分类决策的3种动作行为，即确定将对象x分类到其正域中x∈POS(X)，分类到其负域x∈NEG(X)和分类到其边界域x∈BND(X)中。当已知一个对象x属于某个状态时，采取不同的动作决策就会产生不同的损失。假设决策误判代价矩阵已由领域专家给出，如表1所示。

Table 1 Misclassification cost matrix表1 决策误判代价矩阵

依据贝叶斯决策理论和决策误判代价矩阵，已知对象x(x∈U)，P⊆C，TP(x)为对象x的P容差类，则对象x采取3种决策产生的期望损失可表示为：

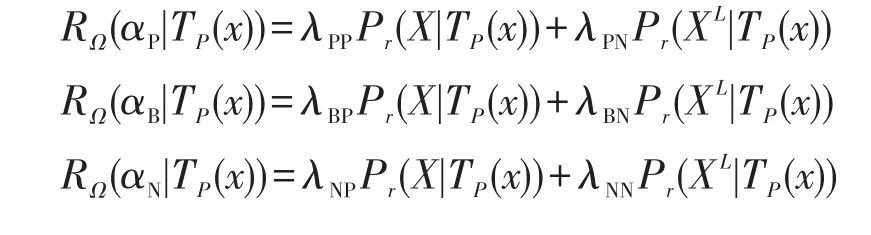
其中，Pr(X|TP(x))和Pr(XL|TP(x))分别表示对象x属于X和不属于X的条件概率。

考虑实际应用的合理情况，对于原本属于X的对象，将其分类到X的正域，其损失小于等于将其分类到边界域的损失，且两者的损失均小于将其划分到负域的损失；反之亦然。即损失函数满足：λPP≤λBP＜λNP，λNN≤λBN＜λPN。

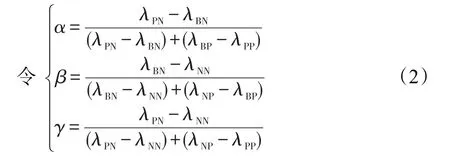
根据Yao三支决策语义规则可知1≥α≥β≥0。对于给定的不完备决策信息系统S=(U,C∪D,V,f)，由决策属性D导出的划分πD={D1,D2,…,Dm}，对∀x∈U，则容差决策粗糙集模型下(α,β)- 正区域、边界域和负区域的决策规则可分别表示如下：

其中Pr(Dmax(TP(x))|TP(x))=表示对象被划分到具有最大概率的决策类。

2.3 多粒度粗糙集

定义1给定一个不完备决策信息系统S=(U,

C∪D,V,f)，令A1,A2,…,Am为条件属性C的m个属性子集，其诱导的容差关系簇为{TA1,TA2,…,TAm}，对于

∀X⊆U，则X关于属性子集A1,A2,…,Am的乐观多粒度粗糙集的下、上近似集可分别定义为：

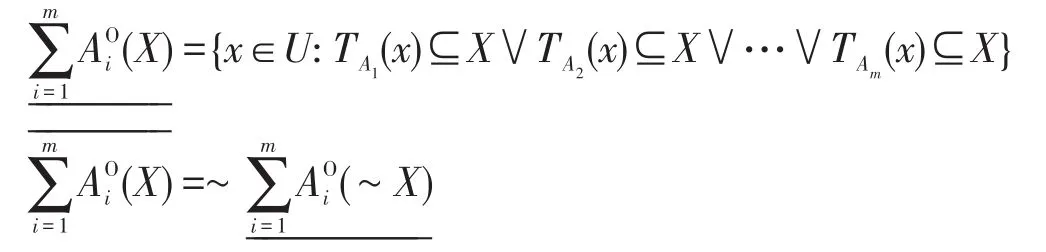
其中～X为X的补集。二元组称为集合X的乐观多粒度粗糙集。

定义2给定一个不完备决策信息系统S=(U,C∪D,V,f)，令A1,A2,…,Am为条件属性C的m个属性子集，其诱导的容差关系簇为{TA1,TA2,…,TAm}，对于∀X⊆U，则X关于属性子集A1,A2,…,Am的悲观多粒度粗糙集的下、上近似集可分别定义为：

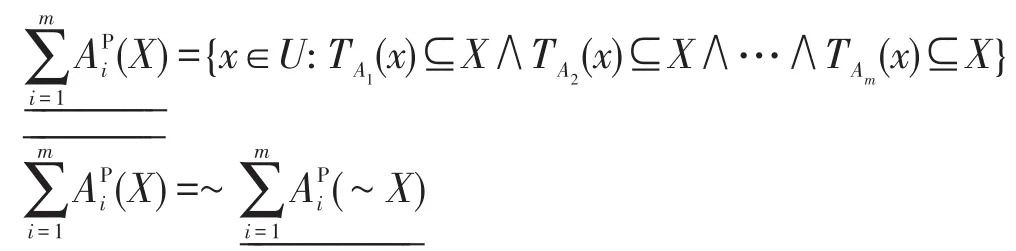
3 多重代价决策粗糙集

由2.2节可以看出，决策粗糙集是基于单个决策误判代价矩阵构建的，且误判代价矩阵通常是由领域专家给定，因而获得的决策规则及决策代价存在局限性。文献[5-6]对多重代价决策粗糙集进行了讨论，构建了乐观代价决策粗糙集和悲观代价决策粗糙集。

设M1,M2,…,Mm为m个不同的决策误判代价矩阵，则第i(i=1,2…,m)个决策误判代价矩阵如表2所示。由m个决策误判代价矩阵，对应得到m个(α,β)阈值，考虑m个阈值中最小值和最大值的情况，根据第i个决策误判代价矩阵和式（2），可计算得到第i个阈值 (αi,βi)为：

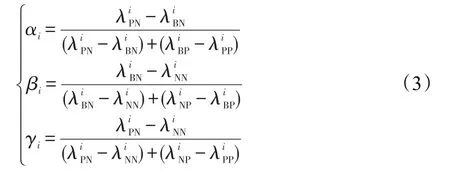
Table 2 i-th cost matrix表2 第i个代价矩阵

根据阈值 (αi,βi)和2.2节中的决策规则（P）、（B）和（N），可分别得到基于容差关系的乐观代价决策规则和悲观代价决策规则。

乐观代价决策规则表示为：

悲观代价决策规则表示为：

若令Pr(Dmax(TP(x))|TP(x))=l，则基于乐观代价决策粗糙集的总体决策代价可定义为：

基于悲观代价决策粗糙集的总体决策代价可定义为：

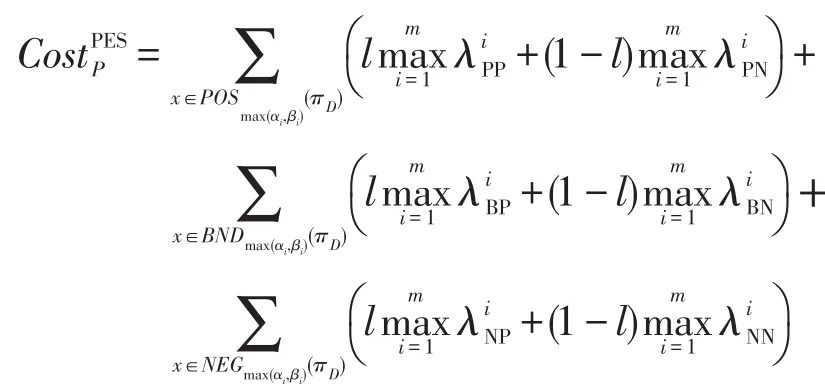
通过研究乐观和悲观代价决策粗糙集来判定决策规则，能预测整个信息系统的最小和最大总体决策代价。但在实际生活中专家给定的误判代价矩阵主观性较强，且每个专家在领域的认可度差别较大，而在智能决策信息系统的研究过程中，人们往往希望获得的决策误判代价更具有代表性和一般性准则，以提高决策规则的可信度。因此，本文将权重均值代价策略引入决策粗糙集中，提出一种基于权重多重代价的决策粗糙集模型。

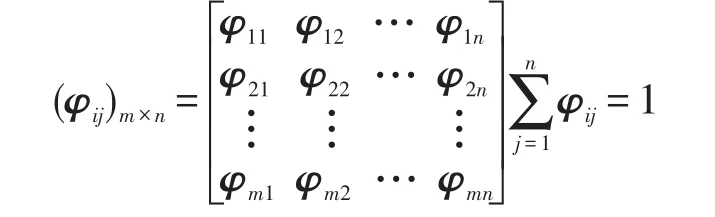
定义3（代价认可度）设M1,M2,…,Mm为m个不同专家给出的决策误判代价矩阵，假设第i个代价矩阵如表2所示。令φij=[φi1,φi2,…,φin]代表领域用户对第i个专家的n个认可度评价，则每个代价矩阵的认可度可通过专家的认可度来描述。m个决策误判代价认可度可用矩阵描述如下：

在实际应用中，可通过计算每位专家n个认可度评价的平均值作为该专家的认可度，则第i个专家的代价认可度权重定义为：

ωi值越大，说明该领域专家在领域用户中的认可度评价越高，其给出的决策代价矩阵可信度越高，因此对应的决策代价矩阵权重越大。记m个代价矩阵的认可度权重为：

根据式（3）和式（4），可计算得到基于权重多代价的阈值 (α′,β′),其值分别为：

则基于权重多重代价的容差决策粗糙集模型正区域、边界域和负区域的决策规则可表示为：

则基于权重多重代价决策粗糙集的总体决策代价可定义为：

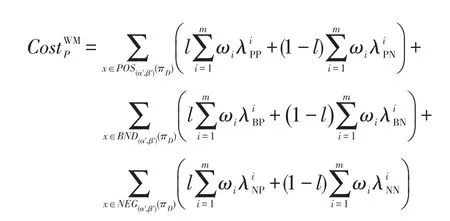
4 基于权重多重代价的多粒度决策粗糙集

4.1 权重多重代价的多粒度决策粗糙集

给定不完备决策信息系统S=(U,C∪D,V,f)，令A1,A2,…,Am为条件属性C的m个属性子集，其诱导的容差关系簇{TA1,TA2,…,TAm}称为m粒度空间结构。假设在每个粒度结构下，其状态集均用Ω={X,XL}表示，对应的决策动作集A={αP,αN,αB}，其决策误判代价矩阵由m个不同的专家给出，其权重记为φ=，假设在每个粒度结构下，决策代价矩阵相同，则任意对象x执行决策αP、αN、αB的期望损失可表示为：

根据三支决策原则和悲观多粒度粗糙集，执行决策αP、αN、αB的期望损失可表示为：

其中∨表示取Pr(X|TAk(x)),k=1,2,…,m中的最大值。

根据三支决策原则和乐观多粒度粗糙集，执行决策αP、αN、αB的期望损失可表示为:

其中∧表示取Pr(X|TAk(x)),k=1,2,…,m中的最小值。

下面将针对基于权重多重代价的悲观多粒度决策粗糙集模型进行分析。由前面描述可知，Pr(X|TAk(x))+Pr(XL|TAk(x))=1，则执行决策αP、αN、αB的期望损失可表示为：

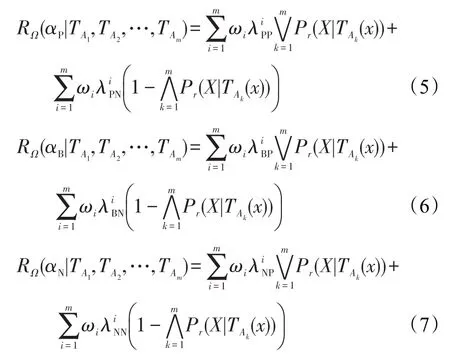
根据贝叶斯风险决策规则可得：

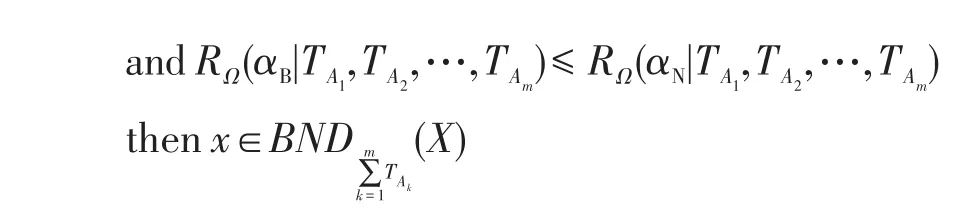
根据规则（PIPI）和式（5）得到：

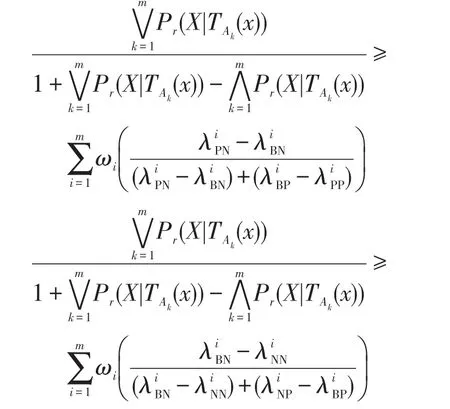
根据规则（PINI）和式（6）得到:

根据规则（PIBI）和式（7）得到：

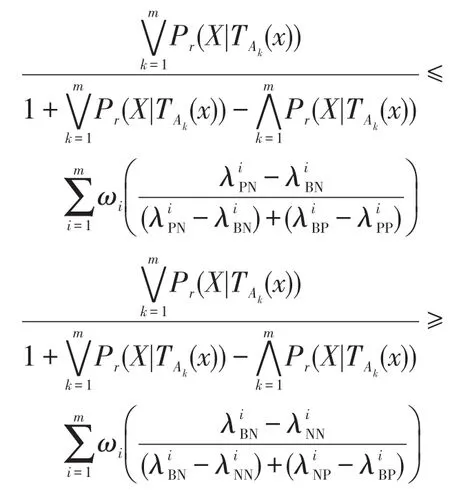
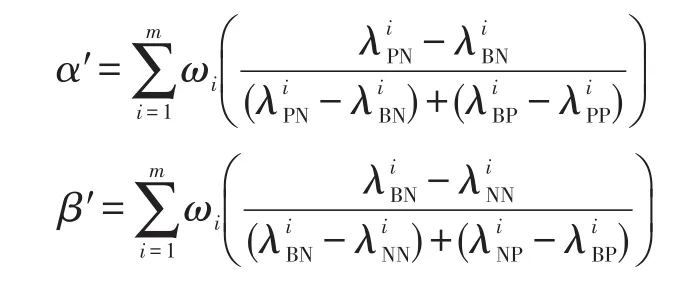
则1≥α′≥β′≥0，得到基于权重多重代价的悲观多粒度决策粗糙集下的正区域、边界域和负区域的决策规则可表示为：

用相同的分析方法，可以得到权重多重代价的乐观多粒度决策粗糙集下的正区域、边界域和负区域的决策规则可表示为：

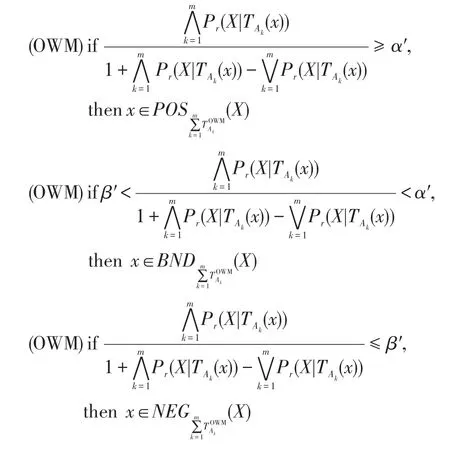
定义4给定一个不完备决策信息系统S=(U,C∪D,V,f)，令A1,A2,…,Am为条件属性C的m个属性子集，其诱导的容差关系簇为{TA1,TA2,…,TAm}，对于∀X⊆U，则X关于属性子集A1,A2,…,Am基于权重多重代价的悲观多粒度决策粗糙集下的正区域、边界域和负区域定义为：

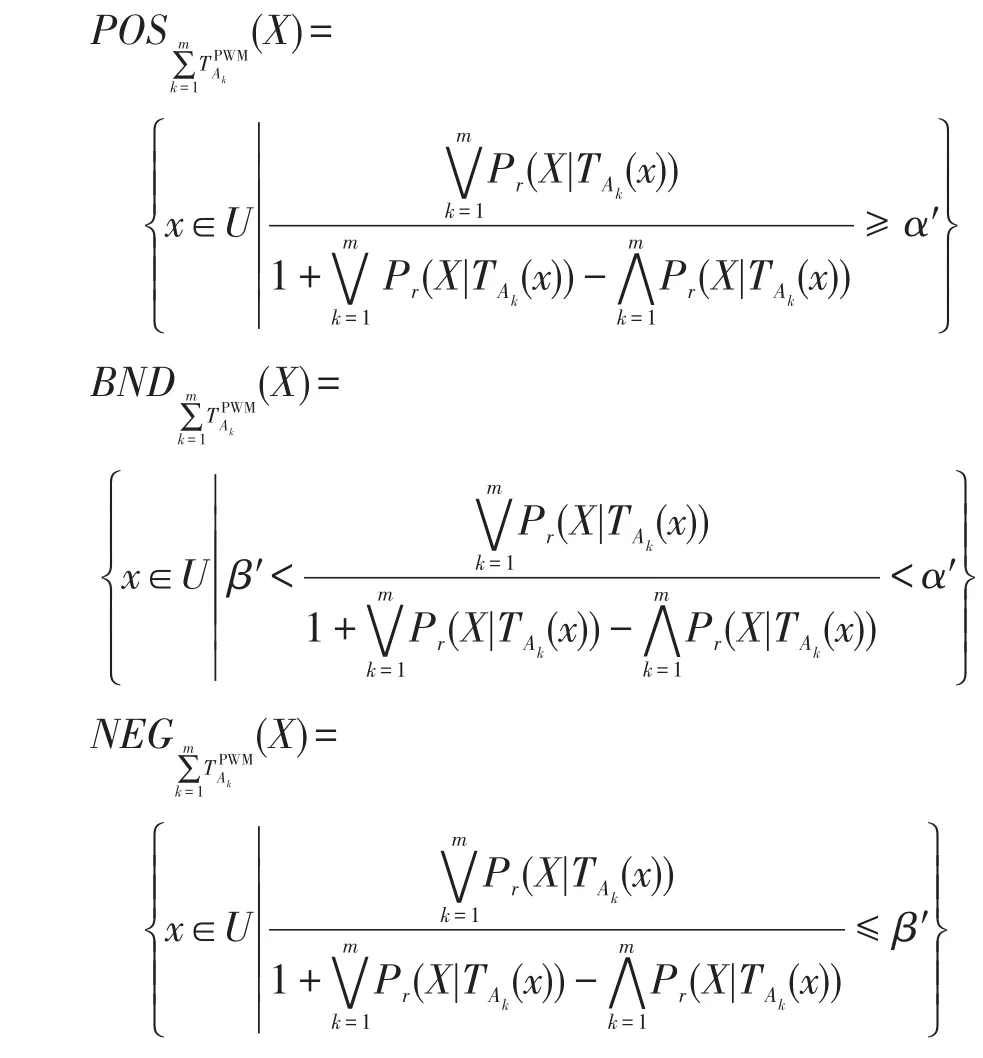
基于权重多重代价的悲观多粒度决策粗糙集X的上、下近似集可定义为：

定义5给定一个不完备决策信息系统S=(U,C∪D,V,f)，令A1,A2,…,Am为条件属性C的m个属性子集，其诱导的容差关系簇为{TA1,TA2,…,TAm}，对于∀X⊆U，则X关于属性子集A1,A2,…,Am基于权重多重代价的乐观多粒度决策粗糙集下的正区域、边界域和负区域定义为：

基于权重多重代价的悲观多粒度决策粗糙集X的上、下近似集可定义为：

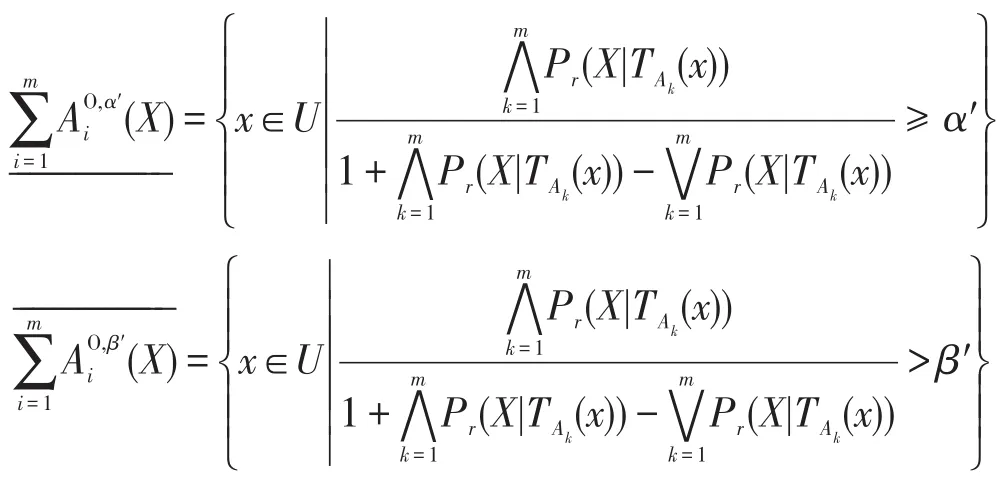
4.2 基于权重多重代价的多粒度决策粗糙集模型相关性质与决策代价

根据权重多重代价的悲观多粒度决策粗糙集模型和乐观多粒度决策粗糙集模型的上、下近似集定义，当α′=1，β′=0时，可以得到：

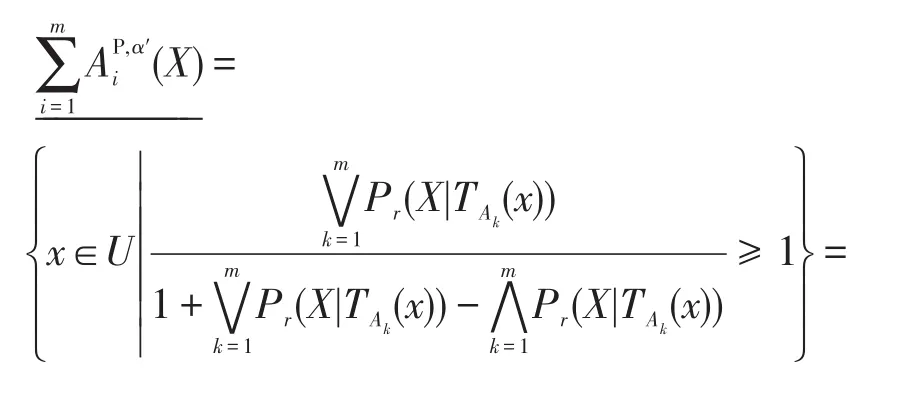
当m=1时，可以得到：

显然，悲观多粒度决策粗糙集当α′=1，β′=0时即为多粒度粗糙集；当m=1时即为决策粗糙集。

定理1设S=(U,C∪D,V,f)是一个不完备决策信息系统，令A1,A2,…,Am为条件属性C的m个属性子集族，P:2U→[0,1]是定义在幂集2U上的概念函数，对任意1≥α′≥β′≥0和X⊆U,有以下性质成立：

以上性质根据定义4和定义5很容易证明。

定义6给定一个不完备决策信息系统S=(U,C∪D,V,f)，令A1,A2,…,Am为条件属性C的m个属性子集，其诱导的容差关系簇为{TA1,TA2,…,TAm}，由决策属性D导出的划分πD={D1,D2,…,Dm}，对∀x∈U，基于权重多重代价悲观多粒度决策粗糙集下的(α′,β′)-正区域、边界域和负区域的决策规则可表示为：

表示在所有满足条件的决策类中，对象x被划分到最大可能性的决策类中，则基于权重多重代价悲观多粒度决策粗糙集的总体决策代价可表示为：

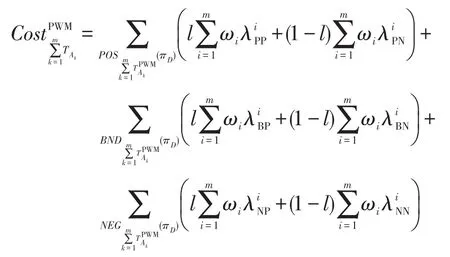
基于权重多重代价乐观多粒度决策粗糙集下的(α′,β′)-正区域、边界域和负区域的决策规则可表示为：

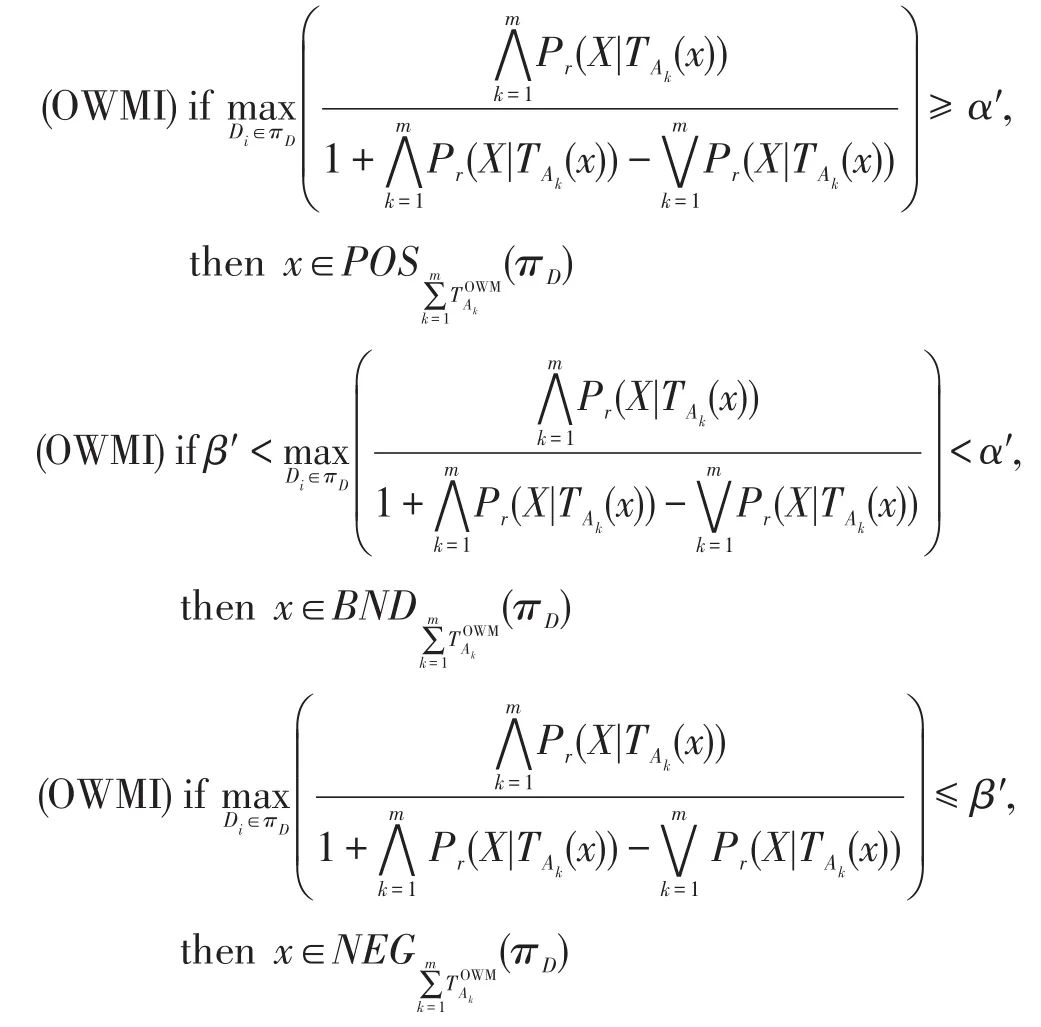
则总体决策代价可表示为：

5 粒度约简方法

属性约简是决策粗糙集理论研究的一个重要内容。在多粒度环境下的目标决策中，通过粒度约简去除那些冗余的知识粒度也是多粒度粗糙集模型中的关键问题。本文将多粒度思想和决策粗糙集模型结合，构建了基于权重多重代价的多粒度决策粗糙集模型，其本质上仍然具有决策粗糙集模型的性质。文献[11-14]从不同角度给出了一系列的决策粗糙集的属性约简方法。文献[12]对决策粗糙集的属性约简准则进行了研究，即决策单调性准则、一般性准则和代价准则。文献[14]讨论了几种与正域相关的决策粗糙集属性约简定义，提出一种保正域不变的决策粗糙集属性约简。下面以基于权重多重代价的悲观多粒度决策粗糙集为例，分析其正域随粒度的变化情况，并提出一种基于最小代价的粒度约简方法。

定理2设不完备决策信息系统S=(U,C∪D,V,f)，令A={A1,A2,…,Am}为条件属性C的m个属性子集族，(α′,β′)为满足条件的一对阈值，给定A′⊆A,X∈U/D，则不成立。

证明若证明不成立，只需找到任意对象x∈AP,α′i(X)满足即可。令粒度空间A′诱导的最大值，最小值，假设Ai∈A′且满足Pr(X|TAi(x))=,则，即若，则满足m≥α′。根据公式：

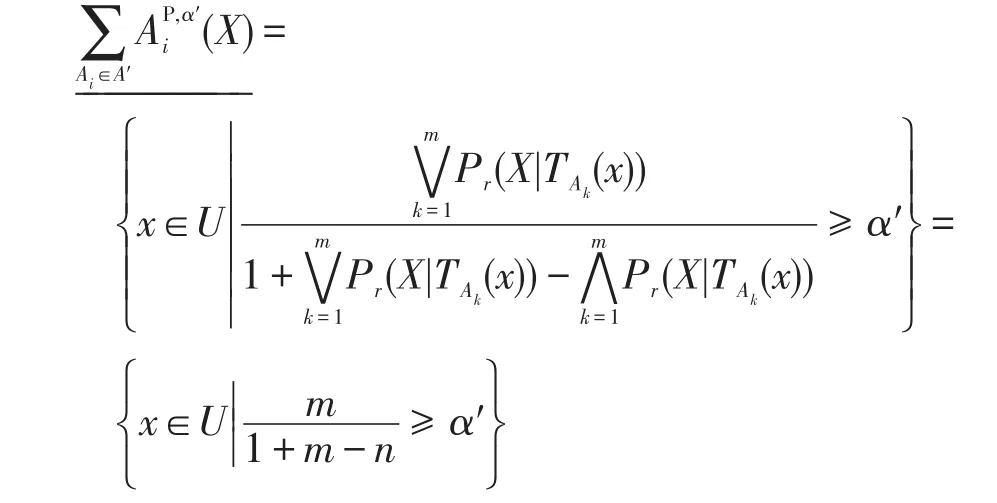
由定理2可知，基于权重多重代价的悲观多粒度决策粗糙集中，其正域并不随粒度的变化而单调性变化，因此采用正域不变的方法对粒度约简在理论性和可解释性上有一定的困难。根据定义6中基于权重多重代价多粒度决策粗糙集的总体决策代价的计算方法，本文以基于权重多重代价悲观多粒度决策粗糙集为例，提出一种基于代价最小的粒度约简定义。

定义7设不完备决策信息系统S=(U,C∪D,V,F)，令A={A1,A2,…,Am}为条件属性C的m个粒度空间集合，其诱导的容差关系簇为{TA1,TA2,…,TAm},知识粒度集A′⊆A是关于权重多重代价悲观多粒度决策粗糙集模型中的一个粒度约简，当且仅当满足：

6 结束语

决策粗糙集模型是根据Bayes风险决策理论，通过分析各种决策的风险代价，从而找出最小风险代价的决策；多粒度粗糙集模型是从多粒度、多层次角度对决策问题进行分析。本文将决策粗糙集和多粒度粗糙集进行有效结合，在分析多重代价决策粗糙集模型和多粒度粗糙集模型的基础上，提出一种基于权重多重代价的多粒度决策粗糙集模型，该模型拓宽了决策粗糙集模型的应用领域；同时，在不完备信息系统中，分析了悲观代价决策粗糙集、乐观代价决策粗糙集和权重多重代价多粒度决策粗糙集模型的决策规则和决策风险代价，并给出了一种基于代价最小化的粒度约简方法，为多粒度粗糙集模型的粒度约简问题提出了一个新思路。

[1]Pawlak Z.Rough sets[J].International Journal of Computer&Information Sciences,1982,11(5):341-356.

[2]Miao Duoqian,Li Daoguo.Rough set theory,algorithm and application[M].Beijing:Science Press,2007.

[3]Yu Hong,Wang Guoyin,Yao Yiyu.Current research and future perspective on decision-theoretic rough sets[J].Chinese Journal of Computers,2015,38(8):1628-1639.

[4]Li Huaxiong,Zhou Xianzhong.Risk decision making based on decision-theoretic rough set:a three-way view decision model[J].International Journal of Computational Intelligence Systems,2011,4(1):1-11.

[5]Dou Huili,Yang Xibei,Song Xiaoning,et al.Decision-theoretic rough set:a multicost strategy[J].Knowledge-Based Systems,2016,91:71-83.

[6]Ma Xingbin,Ju Hengrong,Yang Xibei,et al.Multi-cost based decision-theoretic rough sets in incomplete information systems[J].Journal of Nanjing University:Natural Sciences,2015,51(2):335-342.

[7]Yang Xiaoping,Yao Jingtao.Modelling multi-agent threeway decisions with decision-theoretic rough sets[J].Fundamenta Informaticae,2012,115(2):157-171.

[8]Meng Chao,Yu Jiankun.Merging three-way decisions with decision-theoretic rough sets[J].Computer Systems&Applications,2016,25(4):175-179.

[9]Yao Yiyu.Decision-theoretic rough set models[C]//LNCS 4481:Proceedings of the 2nd International Conference on Rough Sets and Knowledge Technology,Toronto,May 14-16,2007.Berlin,Heidelberg:Springer,2007:1-12.

[10]Yao Yiyu,Zhao Yan.Attribute reduction in decision-theoretic rough set models[J].Information Sciences,2008,178(17):3356-3373.

[11]Jia Xiuyi,Liao Wenhe,Tang Zhenmin,et al.Minimum cost attribute reduction in decision-theoretic rough set models[J].Information Sciences,2013,219:151-167.

[12]Ju Hengrong,Yang Xibei,Yu Hualong,et al.Research on attribute reduction criteria in decision-theoretic rough set[J].Journal of Nanjing Normal University:Natural Science Edition,2015,38(1):41-47.

[13]Ma Xi'ao,Wang Guoyin,Yu Hong.Heuristic method to attribute reduction for decision region distribution preservation[J].Journal of Software,2014,25(8):1761-1780.

[14]Huang Guoshun.Positive region preservation reducts in deci-sion-theoretic rough set models[J].Computer Engineering andApplications,2016,52(2):165-169.

[15]Qian Yuhua,Liang Jiye,Yao Yiyu,et al.MGRS:a multigranulation rough set[J].Information Sciences,2010,180(6):949-970.

[16]Zhang Ming,Cheng Ke,Yang Xibei,et al.Multigranulation rough set based on weighted granulations[J].Control and Decision,2015,30(2):222-228.

[17]Xu Yi,Li Ce.A variable precision multi-granulation rough set model based on multiple thresholds[J].Computer Engineering and Science,2016,38(8):1727-1734.

[18]Meng Huili,Ma Yuanyuan,Xu Jiuchen.Granularity reduction of variable precision pessimistic multi-granulation rough set based on granularity entropy of lower approximate distribution[J].Computer Science,2016,43(2):83-85.

[19]Yao Yiyu,She Yanhong.Rough set models in multigranulation spaces[J].Information Sciences,2016,327:40-56.

[20]Ju Hengrong,Li Huaxiong,Yang Xibei,et al.Cost-sensitive rough set:a multi-granulation approach[J].Knowledge-Based Systems,2017,123:137-153.

[21]Qian Yuhua,Zhang Hu,Sang Yanli,et al.Multigranulation decision-theoretic rough sets[J].International Journal ofApproximate Reasoning,2014,55(1):225-237.

[22]Yang Hailong,Guo Zhilian.Multigranulation decision-theoretic rough sets in incomplete information systems[J].International Journal of Machine Learning and Cybernetics,2015,6(6):1005-1018.

[23]Xu Weihua,Guo Yanting.Generalized multigranulation doublequantitative decision-theoretic rough set[J].Knowledge-Based Systems,2016,105:190-205.

[24]Liu Caihui,Pedrycz W,Wang Meizhi.Covering-based multigranulation decision-theoretic rough sets[J].Journal of Intelligent&Fuzzy Systems,2017,32(1):749-765.

[25]Qian Yuhua,Liang Xinyan,Lin Guoping,et al.Local multigranulation decision-theoretic rough sets[J].International Journal ofApproximate Reasoning,2017,82:119-137.

附中文参考文献:

[2]苗夺谦,李道国.粗糙集理论、算法与应用[M].北京:科学出版社,2007.

[3]于洪,王国胤,姚一豫,等.决策粗糙集理论研究现状与展望[J].计算机学报,2015,38(8):1628-1639.

[6]马兴斌,鞠恒荣,杨习贝,等.不完备信息系统中的多重代价决策粗糙集[J].南京大学学报:自然科学版,2015,51(2):335-342.

[8]孟超,余建坤.三支决策与决策粗糙集融合模型[J].计算机系统应用,2016,25(4):174-179.

[12]鞠恒荣,杨习贝,于化龙,等.决策粗糙集的属性约简准则研究[J].南京师大学报:自然科学版,2015,38(1):41-47.

[13]马希骜,王国胤,于洪.决策域分布保持的启发式属性约简方法[J].软件学报,2014,25(8):1761-1780.

[14]黄国顺.保正域的决策粗糙集属性约简[J].计算机工程与应用,2016,52(2):165-169.

[16]张明,程科,杨习贝,等.基于加权粒度的多粒度粗糙集[J].控制与决策,2015,30(2):222-228.

[17]徐怡,李策.基于多重阈值的变精度多粒度粗糙集模型[J].计算机工程与科学,2016,38(8):1727-1734.

[18]孟慧丽,马媛媛,徐久成.基于下近似分布粒度熵的悲观多粒度粗糙集约简[J].计算机科学,2016,43(2):83-85.