ELM优化的深度自编码分类算法*

徐 毅，董 晴，戴 鑫，宋 威

江南大学 物联网工程学院，江苏 无锡 214122

1 引言

近年来，随着人工智能、机器学习、数据挖掘的发展，神经网络算法的研究一直受到学者们的关注。2006年，Hitton教授提出了“深度学习”[1]的概念，深度学习方法实际上是一种深层神经网络框架，在图像、语音、目标检测等方面取得了很好的效果[2-4]。作为深度学习中经常用到的基础模块，自动编码机[5]（autoencoder）可以从大数据中有效提取特征。为了提高特征提取性能，不断有学者对此进行改进及应用。如Vincent等人[6]提出了一种降噪自动编码机，随机破坏输入特征中的一些数据，输出数据仍使用原始数据，自编码网络根据原始数据估计被破坏的值，这样网络的泛化能力更强。胡帅等人[7]将多层降噪自编码神经网络与欠采样局部更新的元代价算法结合，进一步应用于临床分类诊断，提高了分类模型的辅助诊断性能。秦胜君等人[8]将稀疏自动编码机（sparse autoencoder，SAE）和深度置信网络（deep belief network，DBN）结合，建立SD算法进行文本分类。目前自编码神经网络在现实应用中取得了一定的效果，但仍然存在一些共性不足：当特征维数比较小时，难以提取有效的特征；训练过程繁琐困难，需要大量迭代计算，耗费时间。

针对上述问题，本文提出一种极限学习机（extreme learning machine，ELM）优化的深度自编码神经网络算法。ELM是一种简单有效的单隐层前馈神经网络[9-11]，可调参数少，无迭代过程，吸引了许多学者对其进行研究[12-13]，本文将ELM与自动编码机相结合能有效减少训练时间。本文算法在分类过程中，把ELM作为自编码块，将自动编码机原始的无监督学习转化为监督学习，即在各输出层中加入标签节点，比对实际输出与各样本的期望标签，从而在深度学习过程中实现分类训练。为验证本文方法的有效性，在多个UCI数据集中进行广泛的测试。实验结果表明，与其他自编码网络和传统的RBF（radial basis function）神经网络相比，本文算法具有良好的分类准确率，并且有效地提高了训练速度。

2 相关工作

2.1 自编码神经网络

自动编码机是深度神经网络的常用基础模块，是一种三层神经网络，包括输入层L1、隐含层L2和输出层L3。自动编码机是一种使输出等于输入的无监督学习算法，训练样本集合没有类别标签，含P个训练样本，设为 {x(1),x(2),…,x(i),…,x(p)}，其中x(i)∈Rn，输出y=x，其网络结构如图1。

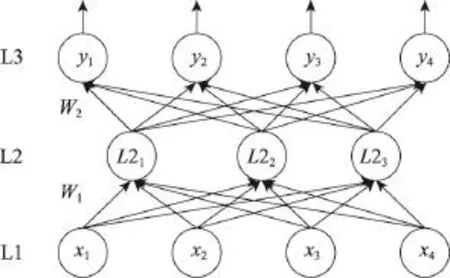
Fig.1 Network structure of autoencoder图1 自动编码机网络结构图

隐藏层L2的输出满足公式：

其中，f(x)=1/(1+e-x)为sigmoid函数；W1为输出层与隐含层之间的权值矩阵；b1为偏置向量。输出层L3满足公式：

由于自动编码机的特殊映射关系，通常定义W2是W1的转置矩阵，b2是隐含层与输出层之间的偏置向量。样本数据由输入层到隐含层看作编码过程，隐含层到输出层看作解码过程。每一个训练样本x先映射到L2，然后再重构成y，每个样本的误差函数为：

总误差函数为：

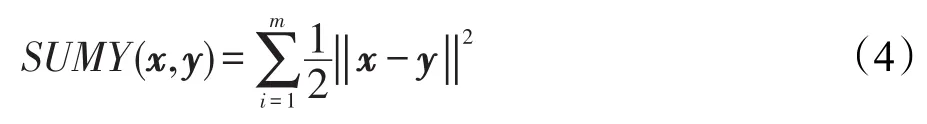
其中，m为训练样本的数量，通过最小化误差函数来优化参数。

对于特征维数较大的样本，隐含层即编码层，可以看作是特征的另一种表达，有效降低了特征维数，为接下来的分类工作降低了难度，减少了计算时间。但当特征维数比较少时，自编码网络的作用难以发挥。

2.2 极限学习机

ELM是一种简单的三层前馈神经网络，输入权值矩阵W和偏置向量b是随机生成的，只需要计算输出权值矩阵β。对K个训练样本，{X,Y}={xi,yi}，i=1,2,…,k，xi∈Rn是n维输入特征，yi是目标向量，训练ELM的数学模型与图1类似，但是输出层L3的输出向量是标签。为了便于介绍，与自动编码机区分，将图1中的W2记作β，数学模型如下：

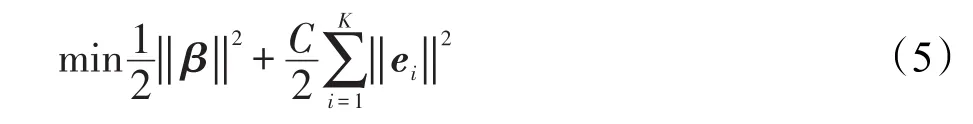
其中，ei=yi-h(xi)β,i=1,2,…,K；C是训练误差的惩罚系数；h(xi)是样本xi在隐含层的输出。得到下面的等价问题：

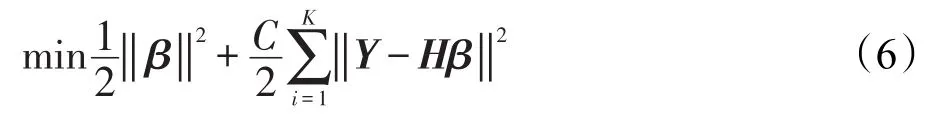
其中，H=[h(x1)T,h(x2)T,…,h(xK)T]T，为了得到上述问题的最优解，将上述目标函数的梯度设置为0，得到下面等式：

通过计算，式（7）的最优解如下：

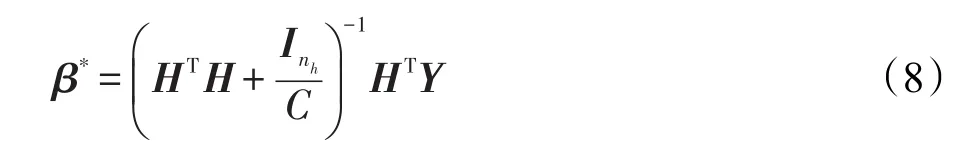
其中，是nh维的单位矩阵。

3 基于ELM的自编码深度神经网络算法

3.1 RP-ELM方法

随机映射（random projection，RP）[14]使用适当的缩放随机矩阵，能够将独立的正态分布数据映射到低维空间，是一种简单有效的降维技术。当样本数据维数较大时，使用RP技术降低维数。RP来源于JL引理（Johnson-Lindenstrauss lemma）[15]：d维欧式距离空间中的任意N个点可以被映射到r维空间，其中r≥O(ε-2ln(N))，并且任意两点之间歪曲的距离不超过1±ε，ε∈(0,1)。在r维空间中，RP能够近似保留N个数据向量之间的距离。Richard等人[15]提出，在2.2节中的矩阵W由式（9）生成：

其中，Wi,j有1/2的概率等于的概率等于，这种随机矩阵既满足JL引理也满足受限等距限制，这就在RP和ELM之间建立了联系。当样本维数过大时，使用RP技术降维，有效减少了计算时间，提高了运算效率。

3.2 深度ELM结构

深度ELM由多个ELM连接而成，输入层的输入数据是训练特征样本或测试特征样本，X∈RN×1，N为特征维数，输入层通过全连接矩阵Wp1∈RM×N连接第一个ELM块隐含层（神经元个数M），隐含层的输出为x1=Wp1X∈RM×1。第i个隐含层单元的输出由sigmoid函数给出：

式（8）计算第一个ELM块的输出权值矩阵β1，并得到输入向量的近似解̂1。以近似解̂1作为第二个ELM块的输入数据，同样的方法计算第二个ELM块的输出权值矩阵β2，得到输入向量的近似解2。之后的ELM块计算均使用以上方式，最后得到一个深度ELM结构。传统的ELM是一种单隐层前馈神经网络，这种浅层网络的学习效果是有限的，而本文提出的ELM优化的深度结构可以更好地学习特征，从而取得更好的分类结果。

3.3 深度ELM监督自编码

在ELM中，当把输入特征作为目标输出，即输 出等于输入时，ELM就成为一个类似2.1节介绍的无监督自编码机。受文献[16]启发，一个简单的方法是在训练样本中加入标签，若有K个训练样本，{X,Y}={xi,yi}，i=1,2,…,k，xi是输入特征，yi是目标向量。设有M个分类，若样本i属于第1类，则yi=[1,-1,-1,…,-1]，若属于第2类，则yi=[-1,1,-1,…,-1]，若属于第M类，则yi=[-1,-1,-1,…,1]。将目标向量加入原始输入特征，目标输出向量为yi+xi，使自动编码机变为监督学习。在深度ELM自编码结构的训练过程中，第一个ELM块的输入数据是原始特征，期望输出是带标签的特征，即加入目标向量的特征，实际输出作为第二个ELM块的输入数据，依然以带标签的特征作为期望输出，计算得到实际输出。之后的ELM块是同样的过程，在这种深度结构中不断学习，不断向期望输出逼近，取实际输出目标向量中的最大值作为预测分类值，直至最后的分类准确率符合分类需求。算法的网络结构如图2。

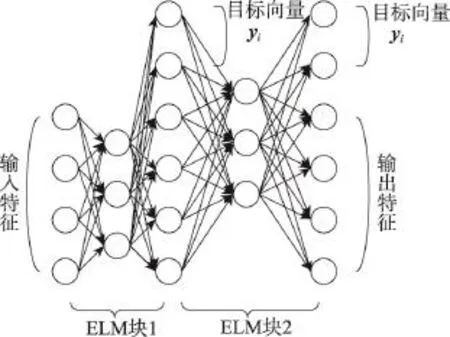
Fig.2 Network structure of ELM optimized deep autoencoder classification algorithm图2 ELM优化的深度自编码算法网络结构图

整个算法主要过程描述如下：

输入：k个n维原始特征样本{x(1),x(2),…,x(i),…,x(k)}，x(i)∈Rn。

输出：加入目标向量的特征样本{x(1),x(2),…,x(i),…,x(k)}，x(i)∈ Rn+M。

步骤1确定自动编码机的隐含层神经元个数及ELM块数。

步骤2将目标向量加入到原始特征中，构成期望输出。

步骤3确定样本特征维数，若维数较大需要降维，使用式（9）生成输入层与隐含层间的权值矩阵W，若不需要降维，跳过此步。

步骤4利用式（8）计算隐含层与输出层间的权值矩阵β。

步骤5利用β计算实际输出，取实际输出中目标向量的最大值作为预测分类值。

步骤6判断分类准确率是否满足要求，若满足要求，算法结束；若不满足要求，增加ELM块数，并返回步骤1。

4 实验结果及分析

4.1 实验数据集

为了验证本文算法的有效性，在UCI Machine Learning Repository上的iris、wine、breastcancer、skin_nonskin、glass、seeds、covtype、LSVT和urbanlandcover数据集上进行实验（数据集出自http://archive.ics.uci.edu/ml/）。所有的数据集均是随机选取2/3作训练数据集，剩下的1/3作测试数据集。各个数据集的基本情况见表1。

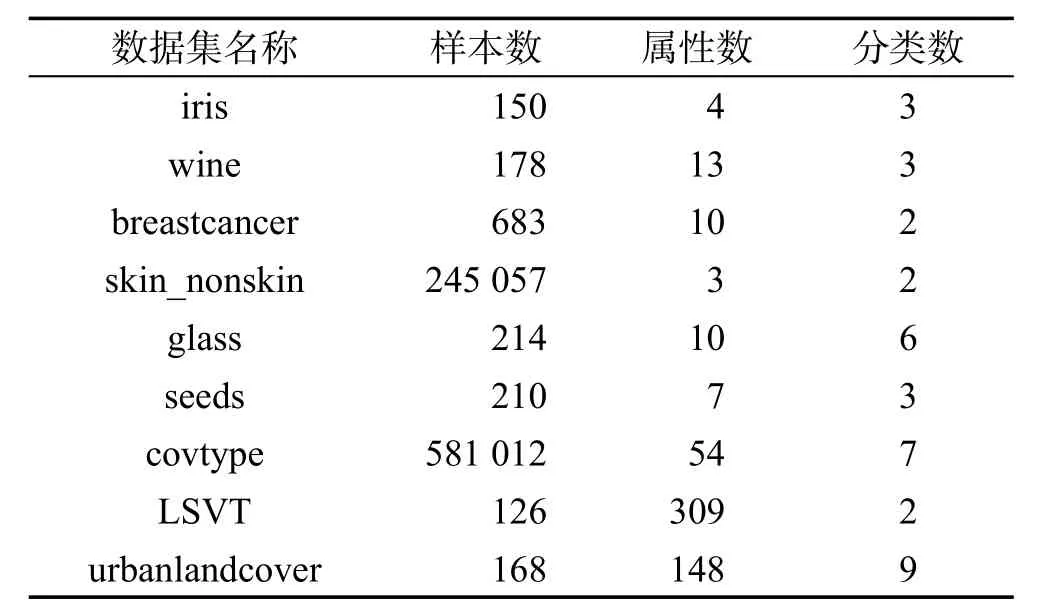
Table 1 Introduction to data sets表1 数据集介绍

4.2 实验结果分析

使用本文算法在UCI的9个数据集上进行实验，分别在module为1、2、4、6的情况下计算分类准确率，module数是ELM块数，即网络的深度。

图3中，（a）是iris数据集的训练数据准确率，（b）是测试数据准确率。数据集中一共有150组数据，为了避免偶然性，做多次实验并计算实验结果的平均值，每次实验从全部150组数据中随机取100组数据进行训练，50组数据进行测试，一共进行100次实验，计算平均值作为最后的实验结果。当深度为2，隐含层神经元为24时，测试准确率最高为95.78%。

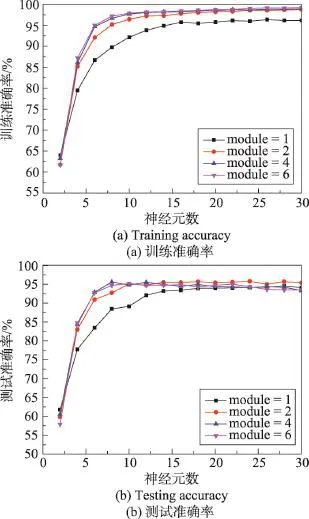
Fig.3 Experimental results on iris dataset图3 iris数据集上的实验结果

图4 是iris数据集在隐含层神经元个数为24，深度为2时的100次随机实验结果。其中图4（a）展现了这100次随机实验的训练准确率和测试准确率，从中可以看出测试的准确率基本保证在90%以上，取平均值后，得到最终测试准确率95.78%。图4（b）展现了训练时间和测试时间，可以看出训练时间较短，即使最长也不会超过0.1 s，保证了学习效率。

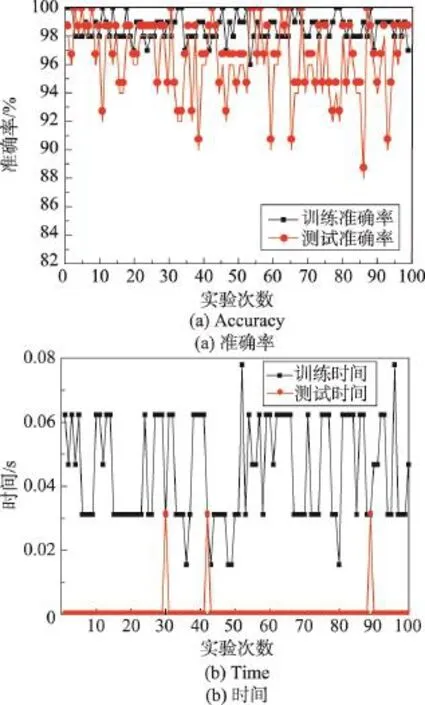
Fig.4 Results of 100 experiments of 2 hidden layers and 24 neurons in iris dataset图4 iris数据集上隐含层神经元24深度2的100次实验结果

图5 是skin_nonskin数据集的实验结果。对于skin_nonskin数据集来说，由于此数据集有245 057组数据，数据过于庞大，为了节约时间，做10次实验后得到平均值。当ELM块的数量一定时，随着隐含层神经元个数的增加，不论是训练准确率还是测试准确率均得到提高，当神经元数量小于14时，准确率的提升比较明显，达到14后，准确率的提升不如之前显著，逐渐趋于稳定。从图中可以看出，ELM块数是1时，准确率不是很高，当块数增加时，准确率有所提高。在skin_nonskin数据集上，当ELM块数为4，即深度为4时，测试的准确率最高达到97.05%。

图6是在breastcancer数据集上的实验结果。隐层神经元数量在范围[2,30]之间，测试数据准确率在ELM块数是1时普遍是最低的，当ELM块数是4时，准确率较高，神经元个数在10之后时基本稳定在97%左右。

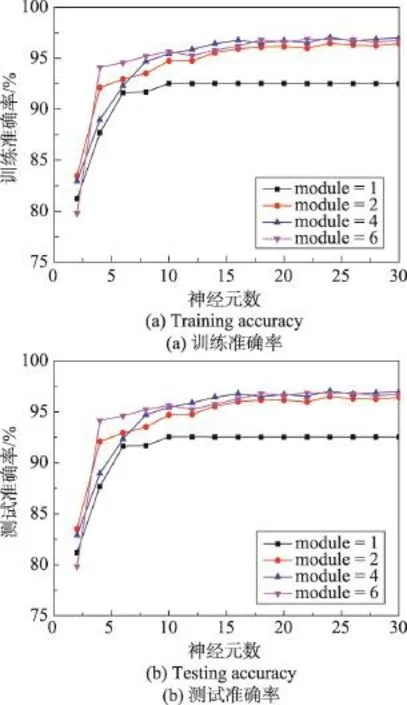
Fig.5 Experimental results on skin_nonskin dataset图5 skin_nonskin数据集上的实验结果

以上 iris、skin_nonskin、breastcance数据集和其他6个数据集上的最佳实验结果如表2。

与DBN算法和RBF神经网络算法的准确率对比实验结果如表3。

与DBN算法和RBF神经网络算法的训练时间对比实验结果如表4。

从表3中可以看出，本文算法（DELMAE）取得了良好的准确率，在breastcancer、wine、seeds、covtype、LSVT、urbanlandcover数据集上的表现均要优于DBN算法、RBF神经网络算法和ELM算法，在iris、skin_nonskin、glass数据集上虽然不是最佳准确率，但是分类效果与最佳准确率相差并不多，在可以接受的范围内。从表4数据可以看出，在9个数据集中，与DBN算法和RBF神经网络算法相比，本文算法极大地缩短了训练时间，有效地提高了训练效率。

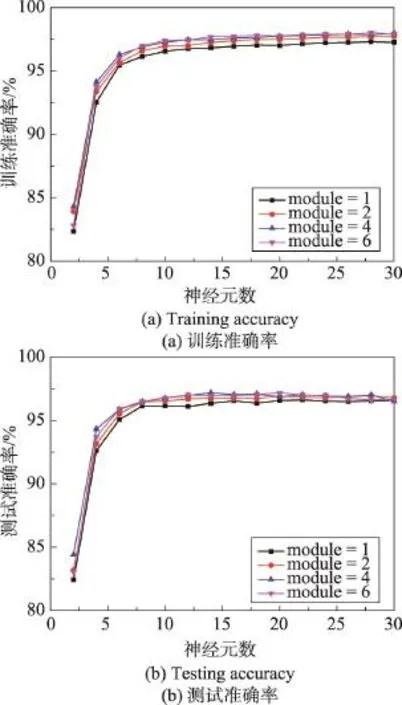
Fig.6 Experimental results on breastcancer dataset图6 breastcancer数据集上的实验结果

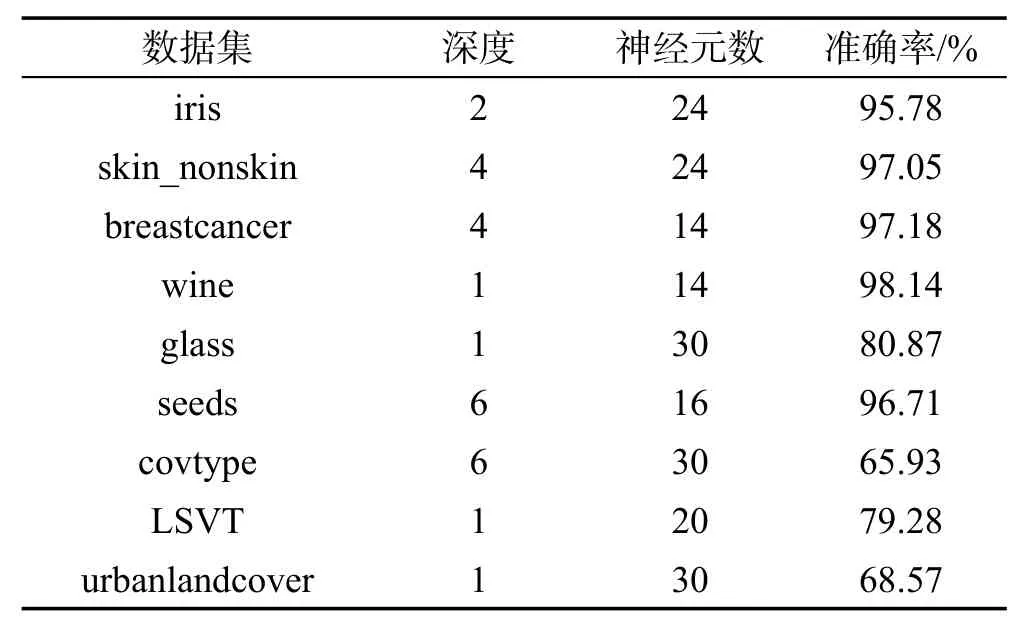
Table 2 Experimental results of accuracy表2 准确率实验结果

以wine数据集为例，图7展示了ELM块数分别为1、2、4、6时在不同的隐含层神经元下的训练时间，隐含层神经元个数范围在[2,30]内，实验结果依然是100次实验取平均值。从图中可以看出，训练时间明显随着深度的增加而增加，在ELM块数为6时，训练时间最大是0.25 s，但是在相同的ELM块数下，受神经元个数的影响比较小，即在深度相同时，训练时间几乎不会随着神经元个数的增加而增加。

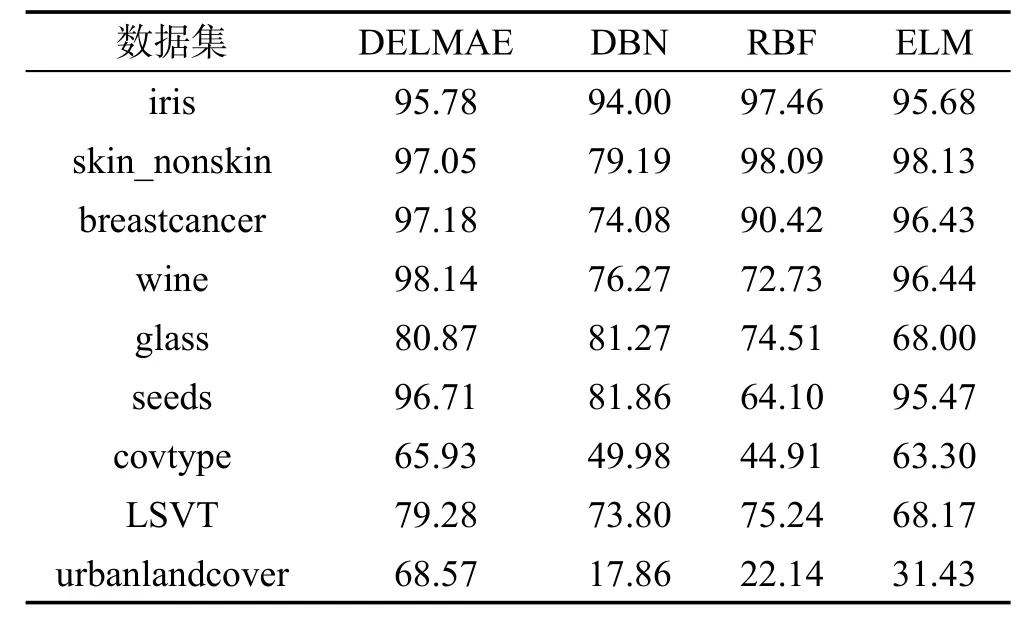
Table 3 Experimental contrast results of accuracy表3 准确率对比实验结果 %

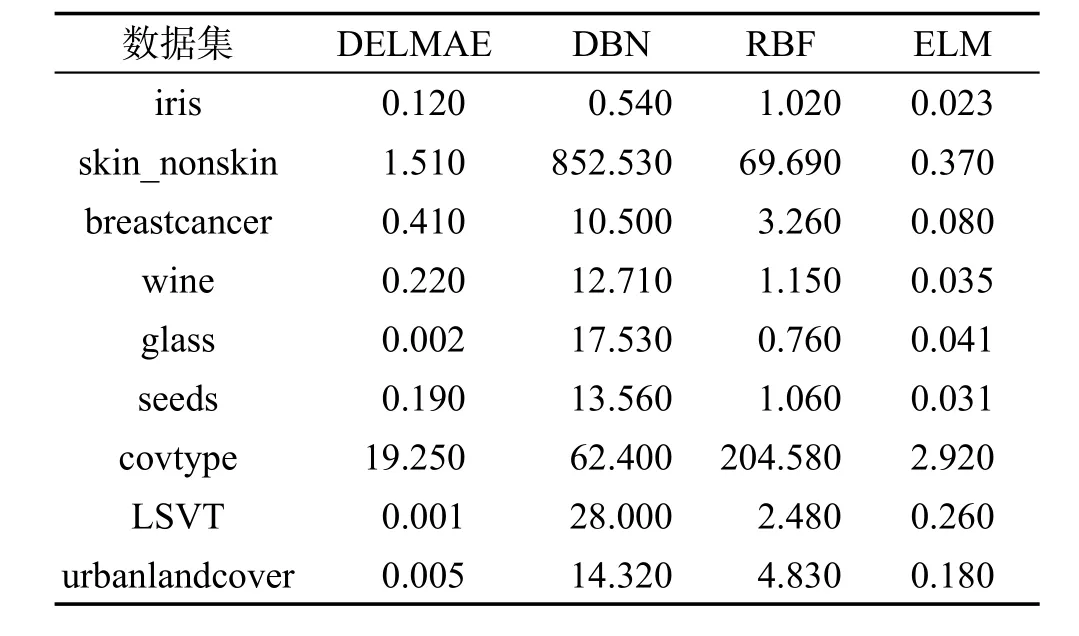
Table 4 Experimental contrast results of training time表4 训练时间对比实验结果 s

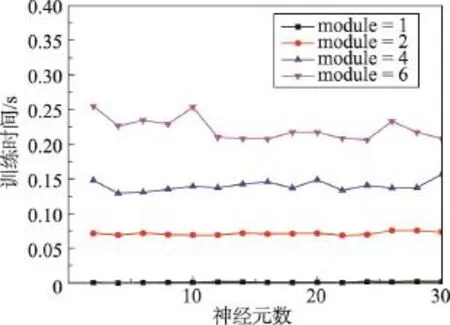
Fig.7 Training time on wine dataset图7 wine数据集上的训练时间

5 结束语

本文提出了一种ELM优化的深度自编码分类算法。为了改善传统的自编码神经网络训练时间长，需要大量迭代计算的缺点，本文算法以ELM作为自编码块，避免了迭代过程。同时对特征维数较大的数据集，采用RP-ELM方法代替传统ELM中的随机输入权值方法，进一步降低特征维数，以减少训练时间。在输出层中加入标签节点，比对实际输出与期望输出，使无监督学习过程转化为监督学习过程。在多个UCI数据集中的实验结果证明，与DBN算法和RBF神经网络算法相比，本文算法的训练时间得到有效减少，提高了训练效率，并且有良好的分类准确率。

[1]Hinton G E,Salakhutdinov R R.Reducing the dimensionality of data with neural networks[J].Science,2006,313(5786):504-507.

[2]Yuan Feiyun.Codebook generation based on self-organizing incremental neural network for image classification[J].Journal of ComputerApplications,2013,33(7):1976-1979.

[3]Cao Meng,Li Hongyan,Zhao Rongrong.A pitch detection method based on deep neural network[J].Microelectronics&Computer,2016,33(6):143-146.

[4]Ouyang Wanli,Wang Xiaogang.Joint deep learning for pedestrian detection[C]//Proceeding of the 2013 IEEE International Conference on Computer Vision,Sydney,Dec 1-8,2013.Washington:IEEE Computer Society,2013:2056-2063.

[5]Wang Haibo.Research of face recognition based on deep learning[D].Hefei:Hefei University of Technology,2014.

[6]Vincent P,Larochelle H,Bengio Y,et al.Extracting and composing robust features with denoising autoencoders[C]//Proceedings of the 25th International Conference on Machine Learning,Helsinki,Jun 5-9,2008.New York:ACM,2008:1096-1103.

[7]Hu Shuai,Yuan Zhiyong,Xiao Ling,et al.Stacked denoising autoencoders applied to clinical diagnose and classification[J].Application Research of Computers,2015,32(5):1417-1420.

[8]Qin Shengjun,Lu Zhiping.Research of text categorization based on sparse autoencoder algorithm[J].Science Technol-ogy and Engineering,2013,13(31):9422-9426.

[9]Huang Guangbin,Zhu Qinyu,Siew C K.Extreme learning machine:a new learning scheme of feedforward neural networks[C]//Proceedings of the 2004 International Joint Conference on Neural Networks,Budapest,Jul 25-29,2004.Piscataway:IEEE,2004,2:985-990.

[10]Huang Guangbin,Zhu Qinyu,Siew C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006,70(1/3):489-501.

[11]Kasun L L C,Zhou Hongming,Huang Guangbin,et al.Representational learning with ELMs for big data[J].Intelligent Systems IEEE,2013,28(6):31-34.

[12]Feng Liang,Ong Y S,Lim M H.ELM-guided memetic computation for vehicle routing[J].IEEE Intelligent Systems,2013,28(6):38-41.

[13]Rong Haijun,Ong Y S,Tan A H,et al.A fast pruned-extreme learning machine for classification problem[J].Neurocomputing,2008,72(1/3):359-366.

[14]Gastaldo P,Zunino R,Cambria E,et al.Combining ELMs with random projections[J].Intelligent Systems IEEE,2013,28(6):46-48.

[15]Baraniuk R,Davenport M,Devore R,et al.A simple proof of the restricted isometry property for random matrices[J].ConstructiveApproximation,2008,28(3):253-263.

[16]Tissera M D,McDonnell M D.Deep extreme learning machines:supervised autoencoding architecture for classification[J].Neurocomputing,2015,174:42-49.

附中文参考文献：

[2]袁飞云.基于自组织增量神经网络的码书产生方法在图像分类中的应[J].计算机应用,2013,33(7):1976-1979.

[3]曹猛,李鸿燕,赵蓉蓉.一种基于深度神经网络的基音检测算法[J].微电子学与计算机,2016,33(6):143-146.

[5]汪海波.基于深度学习的人脸识别方法研究[D].合肥:合肥工业大学,2014.

[7]胡帅,袁志勇,肖玲,等.基于改进的多层降噪自编码算法临床分类诊断研究[J].计算机应用研究,2015,32(5):1417-1420.

[8]秦胜君,卢志平.稀疏自动编码器在文本分类中的应用研究[J].科学技术与工程,2013,13(31):9422-9426.