大规模核方法的随机假设空间方法*
冯 昌,廖士中
天津大学 计算机科学与技术学院,天津 300350
1 引言
大规模核方法是大规模数据分析与挖掘的基本机器学习方法之一。已有工作表明,大规模核方法不仅可给出与深度神经网络相当的学习精度[1],而且模型简单,理论坚实。
核方法是在核诱导的再生核希尔伯特空间(reproducing kernel Hilbert space,RKHS)中训练线性学习器以求解原始学习问题,例如支持向量机(support vector machine,SVM)与核岭回归(kernel ridge regression,KRR)。在高维再生核希尔伯特空间中,核方法训练线性学习器得到的假设具有较好预测性能。但是基于核矩阵的存储与计算使得核方法的计算复杂度至少为O(l2),其中l表示样本规模[2-3]。当训练数据规模较大时,核方法的训练时间过长,存储空间需求过高,从而难以应用于大规模学习问题。
提高核方法可扩展性是核方法学习方法研究一直致力的目标,例如通过分解方法求解对偶二次优化问题的序贯最小优化方法[4]、基于低秩核矩阵近似的算法[5]、并行内点求解法[6]等。在再生核希尔伯特空间中,以上方法虽能在一定程度上缓解核方法对时间和空间的极大需求,但随着噪声样本的增加,支持向量的个数也会线性增加[7]。这将导致核方法不仅在训练阶段,在预测阶段计算开销也将急剧增加。
大规模线性学习算法已有系统研究[8],提出了随机梯度下降法[9]、对偶坐标下降法[10]等。已有结果表明,线性支持向量机虽然在超高维文本和基因分类问题上能取得较好的学习效果,但是对于一般问题,预测精度很难超越核支持向量机[8]。然而,线性或亚线性时间复杂度的求解算法,计算开销小,易于扩展到大规模问题[11],这促进了应用线性学习算法求解非线性问题的研究工作[12-16]。核显式特征表示方法通过显式构造特征映射预处理数据,然后利用预处理后的数据训练线性支持向量机[12]。相比于原始核方法,该方法计算效率高,但只局限于低维的多项式核与串核。
随机傅里叶特征映射方法通过近似平移不变核显式构造特征映射,保证任意两点对应随机特征映射的内积近似其对应的核函数值,为显式构造假设空间求解大规模核方法提供了一种有效途径[14-15]。循环随机特征映射给出一种关于样本维度对数线性时间复杂度的核函数近似方法[16]。本文应用循环随机特征映射构造D维随机假设空间:

其中,α∈ℝD;Π为循环随机矩阵;b为随机向量;C为某一常量;FD为循环随机假设空间。基于拉德马赫复杂性(Rademacher complexity),推导了循环随机假设空间的一致泛化误差界,并给出了其相对于再生核希尔伯特空间中最优假设泛化误差的偏差上界。实验验证了本文方法不仅能够显著地提高非线性核方法的计算效率,而且能够保证预测精度。大规模核方法的随机假设空间方法理论坚实,计算高效,实现简单,是一种大规模核方法的高效实现方法。
2 预备知识
下面简要介绍与循环矩阵有关的基本知识及随机傅里叶特征映射。
2.1 循环矩阵
循环矩阵是一种Toeplitz矩阵,有如下形式:
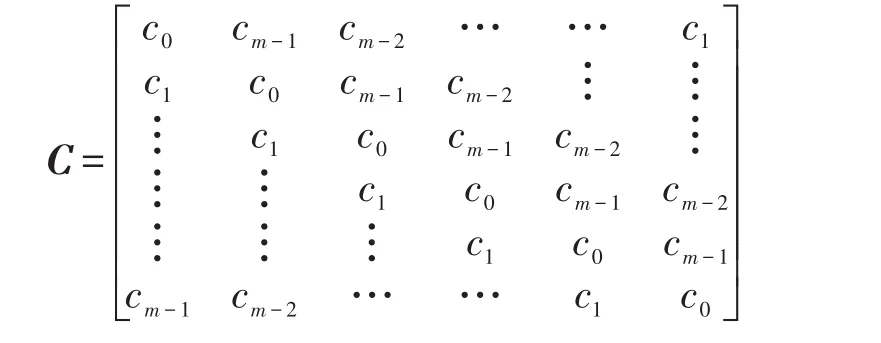
可以看到循环矩阵C的每一列都可由它前一列元素循环向下平移一个元素得到。由此可知,循环矩阵可由它的第一列确定。因此,储存m维循环矩阵的空间复杂度为Θ(m)。循环矩阵有如下离散傅里叶矩阵表示形式[17]。
定理1矩阵C的第一列元素组成的列向量记为c=[c0,c1,…,cm-1]T∈ℝm。C为循环矩阵的充要条件为C有如下离散傅里叶矩阵表示形式:

由定理1可知,对于任意m维向量x,基于快速傅里叶变换(fast Fourier transform,FFT)和快速傅里叶逆变换,循环矩阵投影Cx可在O(mlbm)时间复杂度内计算。
2.2 随机傅里叶特征映射
基于Bochner定理,近似平移不变核可显式构造随机特征映射[14]。
定理2(Bochner定理[18])连续函数f:ℝd↦ℂ 正定,当且仅当f为某一有限非负Borel测度μ的傅里叶变换:

由定理2可知,只要核函数k(⋅)选择合适(归一化),存在一个概率分布p(·)的傅里叶变换与之对应,从而有如下推论。
推论1正定平移不变核K(x,y)=k(x-y)可改写为:
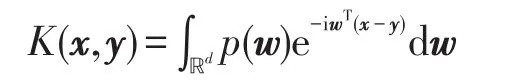
其中,w∈ℝd;p(w)为多维变量概率密度函数。

因此Zw,b(x),Zw,b(y)是高斯核函数的一个无偏估计。通过蒙特卡洛采样方法逼近高斯核,构造如下随机特征映射:

其中,wi∈d是一个高斯随机向量,每一个元素均独立同分布采样于 N(0,1/σ2);bi均匀采样于 [-π,π],i=1,2,…,D。以矩阵形式改写ΦRKS:

其中,W∈D×d为高斯随机矩阵,该矩阵每一个元素均独立采样于N(0,1/σ2);b为均匀随机向量,每一维均独立采样于U[-π,π];cos(·)为逐点映射函数。由此可以看出,RKS由随机投影与余弦变换组成。可证明ΦRKS(x),ΦRKS(y)为高斯核的一个无偏估计,近似的方差为[19-20]:
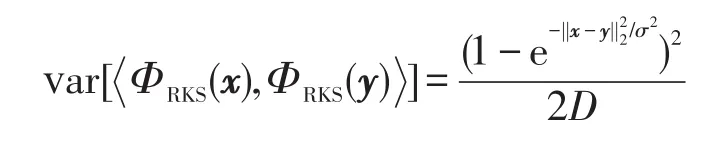
3 循环随机假设空间
首先介绍循环随机特征映射,然后应用循环随机特征映射显式构造循环随机假设空间。
3.1 循环随机特征映射
由定理1可知,若能用具有循环矩阵结构的随机矩阵替代式(2)中的无特殊结构的随机矩阵W,能够显著地提高随机特征映射的计算效率,减少对存储空间的需求。为消除循环矩阵行/列相关性,引入拉德马赫随机变量,定义如下循环随机矩阵。
定义1(循环随机矩阵)矩阵C为m维循环矩阵,第一列元素均独立同分布采样于某一连续概率分布,σ0,σ1,…,σm-1为拉德马赫随机变量 (ℙ[σi=1]=ℙ[σi=-1]=1/2,i=0,1,…,m-1)。称矩阵P=[σ0C0·;σ1C1·;…;σm-1C(m-1)·]为循环随机矩阵,其中Ci·表示循环矩阵C的第i行。
不失一般性,假设d能够整除D,令t=D/d。构造投影矩阵Π=[P(1);P(2);…;P(t)]∈ℝD×d,其中P(i)为循环随机矩阵。用Π代替式(2)中的投影矩阵W,得到循环随机特征映射(circulantrandomfeaturemapping,CRF):

可证明K(x,y)=[ΦCRF(x),ΦCRF(y)],近似方差与RKS近似核函数的方差相同[16]。
3.2 循环随机假设空间
定义2(循环随机假设空间(circulant random hypothesis space,CRHS))基于循环随机特征映射(3)定义如下D维假设空间:
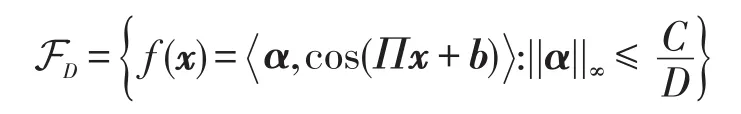
其中α∈ℝD,称之为循环随机假设空间。
定义3(拉德马赫复杂性[21])函数类F的拉德马赫复杂性定义为:

其中σ1,σ2,…,σm为独立同分布拉德马赫随机变量。
引理1循环随机假设空间FD的拉德马赫复杂性:

证明定义集合 S={α∈ℝD:||α||∞≤C/D},集合
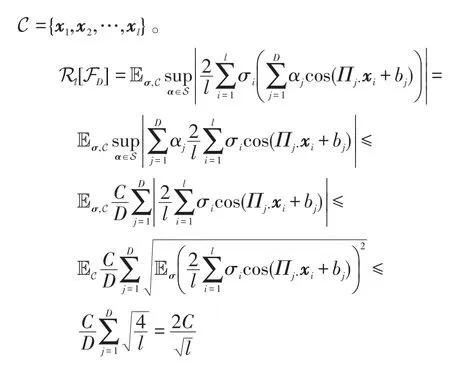
机器学习算法的预测性能一般通过输出假设的泛化误差(generalization error)进行度量。假设的泛化误差定义如下:

其中,ℓ(f(x),y)表示损失函数;P表示X×Y上某个固定但未知的概率分布。正因P未知,所以泛化误差R(f)不可计算,往往通过经验风险(empirical risk)进行估计。经验风险定义:
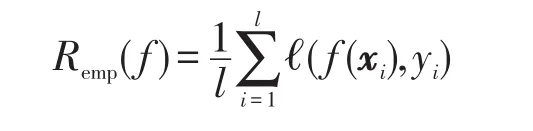
其中,l表示训练样本的规模。循环随机假设空间中任意假设的泛化误差界可由经验风险来界定。
定理3(一致泛化误差)假设间隔损失函数ℓ(y,y′)=ℓ(yy′) 是L-Lipschitz 连续的。对于任意δ∈(0,1),下列不等式至少以1-δ概率成立:

证明基于拉德马赫复杂性,文献[21]给出了期望风险与经验风险之间的关系:
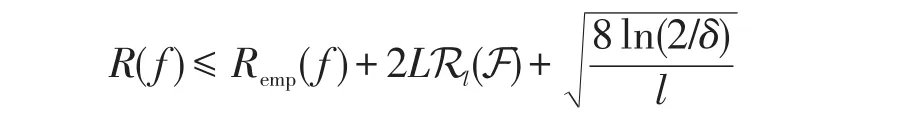
根据引理1可知Rl(FD)的上界为,带入上式即可证明该定理。
令Ω表示循环随机假设空间的参数空间,p(ω)为参数空间上的概率分布。与随机循环假设空间FD对应,定义如下假设类:
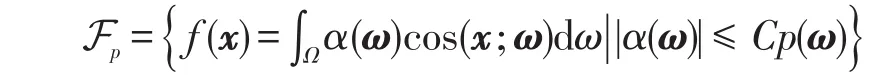
Fp由参数空间Ω上加权余弦函数组成,其权重α(ω)衰减速度高于p(ω)。可证明Fp在再生核希尔伯特空间中是稠密的[22]。因此,再生核希尔伯特空间中假设均可由Fp中假设任意逼近。进一步,可假定目标函数在Fp中,令fp=argminf∈FpR(f),循环随机假设空间中学习算法输出假设记为̂。
定理4假定学习算法的间隔损失函数ℓ(y,y′)=ℓ(yy′)L-Lipschitz连续。训练样本根据某一固定但未知的概率分布独立生成,记为{(xi,yi)l i=1}。循环随机假设空间 FD的随机参数ω1,ω2,…,ωD根据p(ω)独立生成。循环随机假设空间中正则化经验风险最小化算法输出的假设̂满足,对于任意δ∈(0,1/2),下列不等式至少以1-2δ概率成立:

证明类似于文献[23],可证明循环随机假设空间相对于Fp的近似误差界:
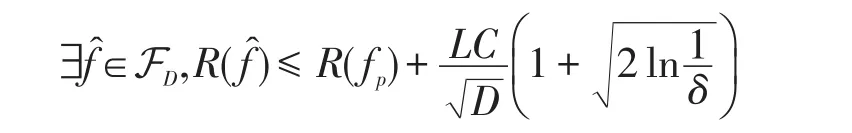
进一步结合循环随机假设空间的一致泛化误差界(定理3)即可证明该定理。
该定理表明在循环随机假设空间中,学习算法输出假设的泛化误差以速度收敛到最优假设fp的泛化误差。因此,循环随机假设空间是一种有理论保证且计算高效的显式假设空间。
类似地,应用RKS[14]与Fastfood[24]构造随机假设空间,分别记为RRHS(RKS random hypothesis space)和 FRHS(fastfood random hypothesis space),其计算复杂度与循环随机假设空间构造的计算复杂度对比如表1所示。
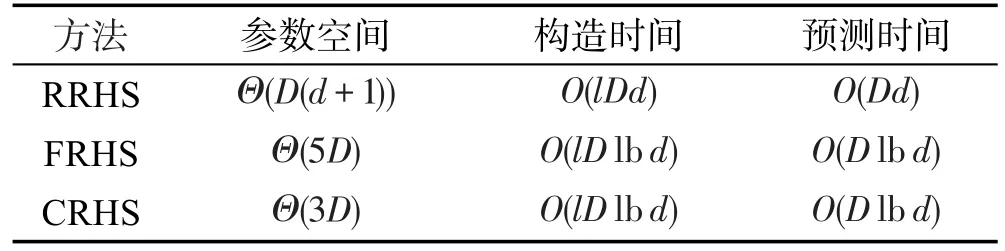
Table 1 Computational complexities of RRHS,FRHS and CRHS表1 RRHS、FRHS与CRHS构造的计算复杂度
4 大规模核方法
下面主要针对分类与回归问题,给出大规模核方法的循环随机假设空间算法。
记样本空间中的数据集合为S={(xi,yi)l i=1},其中xi∈ℝd,对于二分类问题yi={-1,+1},对于多分类问题yi={1,2,…,M1},M1∈ℕ+,对于回归问题yi∈[-M2,M2],M2∈ℝ+,其中i=1,2,…,l。循环随机假设空间是一种显式假设空间,可应用已有的线性/亚线性学习算法求解分类/回归问题。本文提出大规模核方法的循环随机假设空间算法框架,具体描述见算法1。
算法1大规模核方法的循环随机假设空间算法
输入:训练数据S={(xi,yi)li=1},随机假设空间维度D,高斯核参数σ,正则化参数λ。
输出:循环随机假设空间及假设f。
(1)随机生成ω1,ω2,…,ωD~N(0,I/σ2);
(2)随机生成b1,b2,…,bD~U[-π,π];
(3)随机生成σ1,σ2,…,σD~{-1,+1};
(4)构造循环随机矩阵Π及假设空间CRHS;
(5)在CRHS中,利用训练数据S与正则化参数λ,训练正则化线性学习器。
如果一个二元函数K(x,y):X×X→ℝ能够表示成两个一元函数ϕ:X→F内积的形式,即

那么称K(x,y)为核。ϕ(·)往往是超高维甚至是无穷维的,根据优化算法的对偶表示,核方法可以在不知道ϕ(·)具体形式的情形下,仅仅依靠K(·,·)表示学习假设,从而避免了维数灾难,此方法称为核技巧。核K对应的RKHS为:
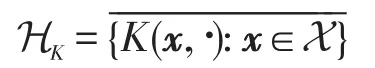
其内积为:

由表示定理可知,目标假设可表示为:
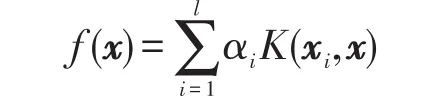
KSVM与KRR可统一地表示为正则化学习问题:
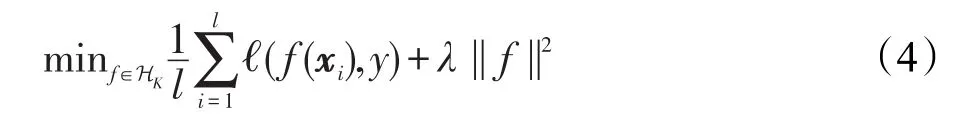
其中,ℓ(·,·)为损失函数;λ为正则化系数。对于支持向量机 ℓ(f(x),y)=max(0,1-yf(x)),对于核岭回归ℓ(f(x),y)=(f(x)-y)2。
算法时间复杂度:在隐式特征空间中,基于核技巧求解式(4)的时间复杂度至少为O(l2),只能适用于中等以下规模学习问题。算法1时间复杂度为O(l),可适用于大规模学习问题。
5 实验结果与分析
针对分类与回归问题,验证大规模核方法的循环随机假设空间算法(CRHS)的有效性与高效性。实验中数据为标杆数据集,包括二分类、多分类、回归数据,如表2所示。
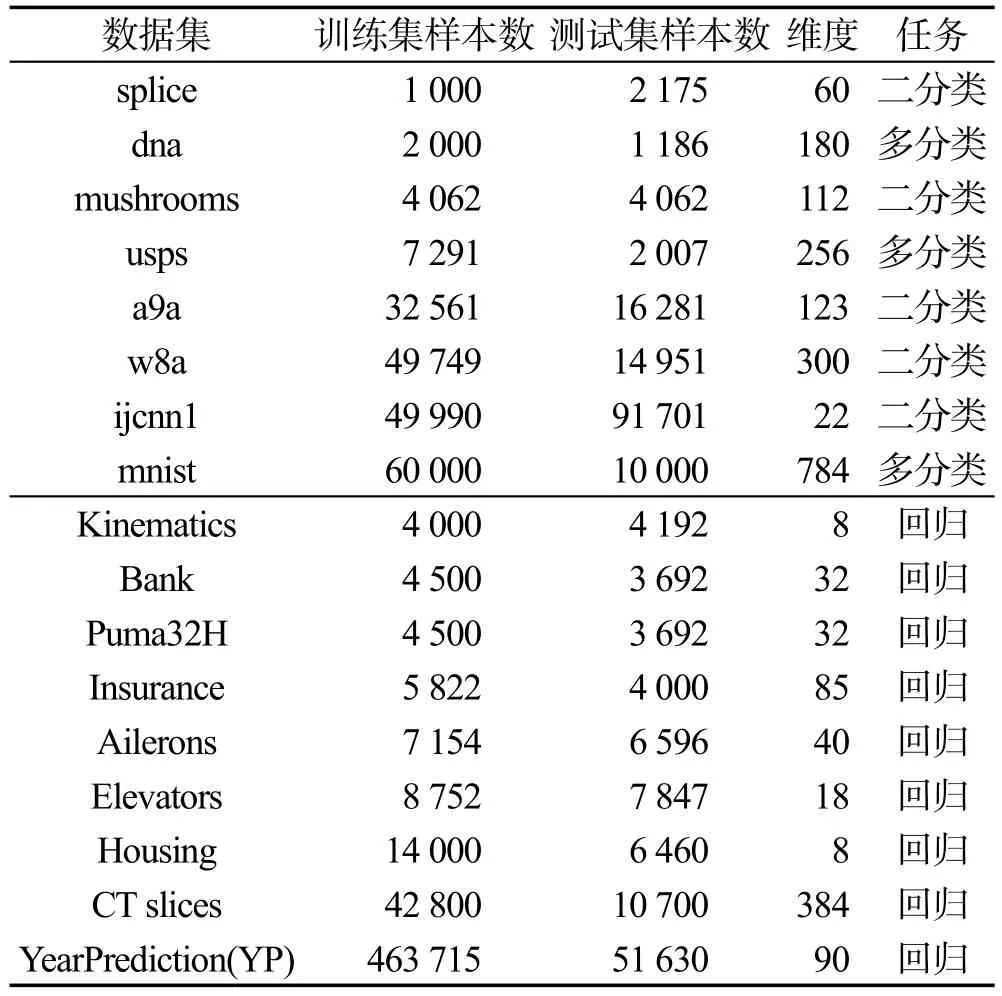
Table 2 Characteristics of datasets表2 数据集说明
对比算法包括大规模核方法的RKS假设空间算法(RRHS)、大规模核方法的Fastfood假设空间算法(FRHS)与精确核方法(Kernel)。高斯核参数γ=1/(2σ2)与正则化参数λ均从备选参数集{2-9,2-7,…,27,29}中选择。对于每一种算法,参数(γ,λ)通过5-折交叉验证确定。假设空间维度D经验地设置为几百到几千。所有随机算法在每个数据集上重复10次,记录平均值及均方误差。实验代码用R语言实现,实验平台为Ubuntu Linux server 16.04,实验环境为2.60 GHz Intel®Xeon®CPU和64 GB内存。
在数据集dna和ijcnn1上,比较RRHS、FRHS和CRHS方法预测准确率随着假设空间维度D变化的情况,实验结果见图1。随着假设空间维度的增加,3种方法的预测准确率快速增加然后趋于平稳。RRHS与CRHS方法的预测准确率基本趋于一致,正好与随机特征映射近似核函数的理论结果相符合。验证了应用循环随机矩阵取代无结构的随机矩阵构造随机特征映射和随机假设空间的有效性。当假设空间维度较低时,在同样的假设空间维度设置下FRHS预测准确率不如其他两种随机假设空间方法。这是因为Fastfood近似核函数的方差比其他两种方法近似核函数方差大。当假设空间维度较低时,其对学习精度的影响不能忽略,FRHS的预测准确率不如其他两种方法。当假设空间维度足够高时,3种方法的预测准确率相当。
在每个数据集上,统一将RRHS、FRHS和CRHS方法的假设空间维度D设置足够高,并与精确核方法相比较,预测精度如表3所示。几乎在所有分类与回归数据集上,3种随机方法都能取得与精确核方法相当或者更高的预测精度。这3种随机方法的预测精度之间并没有显著差别。表4与表5分别给出了不同学习算法对应的训练与预测时间。可以看出,几乎在所有的数据集上,RRHS、FRHS和CRHS的训练与预测效率明显高于精确核方法。除了mnist和CT slices这两个相对高维的数据集,在其他数据集上,FRHS的训练和预测效率明显不如RRHS和CRHS。这是因为FRHS需要通过补0的方式预处理数据以适应快速Hadamard变换。当数据维度较低时,快速Hadamard变换带来的效率提升被数据预处理时间所抵消。因此,只有当数据维度较高时,例如mnist,FRHS的训练与预测效率才显著高于RRHS。然而,所提出的CRHS能够一定程度解决FRHS所面临的问题。一般情况下,当原始数据维度d>100时,CRHS能够在保持预测精度的同时显著地提高训练与预测效率。综上,CRHS是一种高效的大规模核方法学习算法,适用于大规模机器学习。

Fig.1 Testing accuracies of RRHS,FRHS and CRHS with hypothesis space dimension D图1RRHS、FRHS和CRHS的预测准确率随假设空间维度的变化
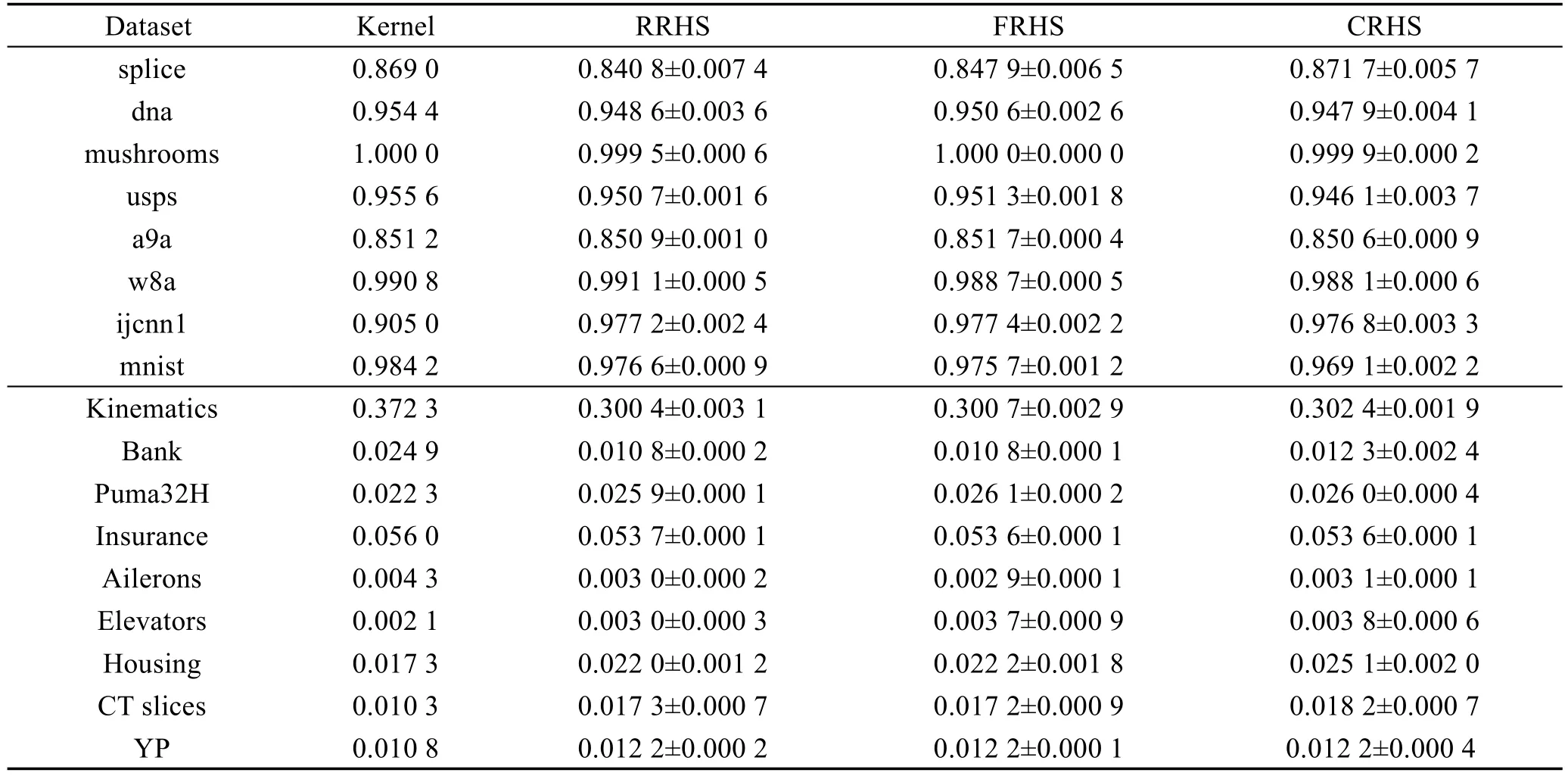
Table 3 Testing accuracies and MSEs on different datasets表3 不同数据集上的测试准确率和均方误差
6 结束语
核方法在高维再生核希尔伯特空间中通过核技巧与二次优化技术寻找一个最优假设以求解样本空间中的非线性学习问题。基于核矩阵的存储与计算使得核方法的计算时空复杂度至少为样本规模的平方级。当数据规模较大时,核方法的训练、预测时间过长,存储空间需求过高,难以应用于大规模学习问题。为此提出大规模核方法的循环随机假设空间方法,一方面能够在关于数据维度对数线性时间复杂度内构造显式假设空间,另一方面在显式假设空间中可应用大量已有的线性或亚线性时间复杂度的线性学习算法来求解非线性问题。循环随机假设空间不仅有一致泛化误差界保证,而且其泛化误差能够以的速率高概率地收敛到最优假设的泛化误差。几乎在所有数据集上,本文方法能够在保证预测精度的情况下,大幅度地提高模型训练与预测效率。
进一步工作考虑循环随机假设空间维度D的设置与概率分布N(0,I/σ2)的选择问题。

Table 4 Training time on different datasets表4 不同数据集上训练时间 s

Table 5 Predicting time on different datasets表5 不同数据集上预测时间 s
[1]Huang P S,Avron H,Sainath T N,et al.Kernel methods match deep neural networks on TIMIT[C]//Proceedings of the 2014 IEEE International Conference on Acoustics,Speech and Signal Processing,Florence,May 4-9,2014.Piscataway:IEEE,2014:205-209.
[2]Vapnik V N.Statistical learning theory[M].New York:Wiley-Interscience,1998.
[3]Schölkopf B,Smola A J.Learning with kernels:support vector machines,regularization,optimization,and beyond[M].Cambridge:MIT Press,2002.
[4]Chang C C,Lin C J.LIBSVM:a library for support vector machines[J].ACM Transactions on Intelligent Systems and Technology,2011,2(3):27.
[5]Drineas P,Mahoney M W.On the Nyström method for approximating a Gram matrix for improved kernel-based learning[J].Journal of Machine Learning Research,2005,6:2153-2175.
[6]Chang E Y,Zhu Kaihua,Wang Hao,et al.PSVM:parallelizing support vector machines on distributed computers[C]//Proceedings of the 21st Annual Conference on Neural Information Processing Systems,Vancouver,Dec 3-6,2007.Red Hook:CurranAssociates,2008:257-264.
[7]Steinwart I.Sparseness of support vector machines[J].Journal of Machine Learning Research,2003,4(6):1071-1105.
[8]Yuan Guoxun,Ho C H,Lin C J.Recent advances of largescale linear classif i cation[J].Proceedings of the IEEE,2012,100(9):2584-2603.
[9]Zhang Tong.Solving large sale linear prediction problems using stochastic gradient descent algorithms[C]//Proceedings of the 21st International Conference on Machine Learning,Banff,Jul 4-8,2004.New York:ACM,2004:919-926.
[10]Fan Rongen,Chang Kaiwei,Hsieh C J,et al.LIBLINEAR:a library for large linear classif i cation[J].Journal of Machine Learning Research,2008,9:1871-1874.
[11]Shalev-Shwartz S,Singer Y,Srebro N,et al.Pegasos:primal estimated sub-gradient solver for SVM[J].Mathematical Programming,2011,127(1):3-30.
[12]Chang Yinwen,Hsieh C J,Chang Kaiwei,et al.Training and testing low-degree polynomial data mappings via linear SVM[J].Journal of Machine Learning Research,2010,11:1471-1490.
[13]Liu Yong,Jiang Shali,Liao Shizhong.Approximate Gaussian kernel for large-scale SVM[J].Journal of Computer Research and Development,2014,51(10):2171-2177.
[14]Rahimi A,Recht B.Random features for large-scale kernel machines[C]//Proceedings of the 21st Annual Conference on Neural Information Processing Systems,Vancouver,Dec 3-6,2007.Red Hook:CurranAssociates,2008:1177-1184.
[15]Feng Chang,Liao Shizhong.Model selection for Gaussian kernel support vector machines in random Fourier feature space[J].Journal of Computer Research and Development,2016,53(9):1971-1978.
[16]Feng Chang,Hu Qinghua,Liao Shizhong.Random feature mapping with signed circulant matrix projection[C]//Proceedings of the 24th International Joint Conference on Artif icial Intelligence,Buenos Aires,Jul 25-31,2015.Menlo Park:AAAI,2015:3490-3496.
[17]Davis P J.Circulant matrices[M].San Francisco:John Wiley&Sons,1979:1-250.
[18]Rudin W.Fourier analysis on groups[M].San Francisco:John Wiley&Sons,2011:1-285.
[19]Sutherland D J,Schneider J G.On the error of random Fourier features[C]//Proceedings of the 31st Conference on Uncertainty in Artif i cial Intelligence,Amsterdam,Jul 12-16,2015.Corvallis:AUAI Press,2015:862-871.
[20]Yu F X,Suresh A T,Choromanski K,et al.Orthogonal random features[C]//Proceedings of the Annual Conference on Neural Information Processing Systems,Barcelona,Dec 5-10,2016.Red Hook:CurranAssociates,2016:1975-1983.
[21]Bartlett P L,Mendelson S.Rademacher and Gaussian complexities:risk bounds and structural results[J].Journal of Machine Learning Research,2002,3:463-482.
[22]Rahimi A,Recht B.Uniform approximation of functions with random bases[C]//Proceedings of the 46th Annual Allerton Conference on Communication,Control,and Computing,Monticello,Sep 23-26,2008.Piscataway:IEEE,2008:555-561.
[23]Rahimi A,Recht B.Weighted sums of random kitchen sinks:replacing minimization with randomization in learning[C]//Proceedings of the 22nd Annual Conference on Neural Information Processing Systems,Vancouver,Dec 8-11,2008.Red Hook:CurranAssociates,2009:1313-1320.
[24]Le Q,Sarlós T,Smola A J.Fastfood—approximating kernel expansions in loglinear time[C]//Proceedings of the 30th International Conference on Machine Learning,Atlanta,Jun 16-21,2013.Brookline:Microtome Publishing,2013:244-252.
附中文参考文献:
[13]刘勇,江沙里,廖士中.基于近似高斯核显式描述的大规模SVM求解[J].计算机研究与发展,2014,51(10):2171-2177.
[15]冯昌,廖士中.随机傅里叶特征空间中高斯核支持向量机模型选择[J].计算机研究与发展,2016,53(9):1971-1978.

