机载激光通信二自由度运动模拟台设计
白杨杨 张立中 孟立新


摘要 机栽激光通信光端机外场实验需要轻小型化姿态运动模拟器。通过对飞机位置姿态变化对激光通信APT(捕获、瞄准、跟踪)系统影响分析,提出了一种具有方位和俯仰功能的新型平行2自由度平台,并利用闭环矢量法建立了运动学模型。通过对Matlab数学模型和ADAMS仿真结果的比较,验证建模方法准确定,为控制系统的设计提供了参考和依据。
【关键词】运动仿真平台 闭环矢量法 激光通信机载
激光通信具有高通信速率、抗干扰、保密性强,低功耗等优点。APT系统作为空间激光通信的基础,是开展激光通信首先需要解决的难题。
高频振动和低频扰动是机载激光通信转台面临的主要因素,转台稳定性受高频振动影响,跟踪性能受低频扰动影响。因此,高频振动与低频扰动在跟瞄转台系统设计时需要着重考虑。常规运动模拟台采用串聯式结构,具有体积大、承载轻特点;并联运动模拟台采用框架式结构,具有体积小、承载重、精度高、无视轴遮挡等优点,适合为野外激光通信跟瞄转台通信试验提供模拟扰动。
1 机载姿态变化分析
高精度激光通信跟踪转台采用粗精复合控制,跟踪速度与加速度直接影响跟踪效果,通过合理选择保精度跟踪速度来满足跟踪精度要求。系统动态滞后误差与保精度角速度、角加速度关系为:
式中,Ω为跟踪角速率,ε跟踪角加速度,Kv为速度品质系数,Ka为加速度品质系数。从式(1)可以看出,动态滞后误差的取决于跟踪系统自身的特性与原始激励。
实际测试试验飞机最大姿态变化约为3.6°/s,最大加速度约为4°/s2。因此,考虑到设备应用扩展,两自由度模拟试验转台的最大模拟速度定为20°/s,最大模拟加速度定为20°/s2,最大运动范围为15°。
2.2一DOF运动模拟台设计
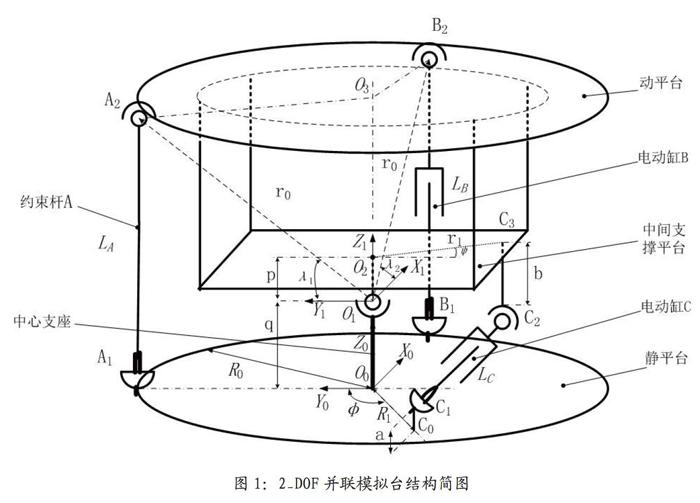
2 DOF运动模拟台结构简图如图1所示,系统由动平台、中间支撑平台(包括四个辅助支撑杆)、中心支座、静平台、约束杆A、伺服电动缸B、伺服电动缸C及其两端支撑杆(coC,和C2C3)外加连接铰链等组成。伺服电动缸B和C同时运动,实现模拟台方位和俯仰的复合运动,该并联机构有2个自由度,与驱动数目相等,因此不存在驱动冗余。
坐标系建立如图1所示,坐标系O0-.X0Y0Z0静平台参考坐标系,坐标系O1-X1Y1Z1为模拟台中心坐标系,两个坐标系的轴系初始状态下分别平行。假设从初始位置起,俯仰先绕Y0轴旋转α角,方位再绕Z0轴转β角得到的当前姿态坐标为(α,β),根据卡尔单角坐标变换关系,得到动平台上任一点e在基坐标
3 动力学仿真分析
根据该运动模拟台设计要求,初始设计参数如下:初始状态下动平台与静平台之间高度315mm,R0=185mm,p=33.5mm;通过仿真计算与结构优化在不考虑铰链间隙、轴系磨损等误差的条件下,根据设计参数建立模拟台的数学模型,并将结构参数代入公式公式(3)、(4)得到两个电动缸杆长实时变化曲线,同时,应用动力学仿真软件Adams建立二自由度模拟台运动学模型。输入方位和俯仰的变化规律,实时测量杆长两端位移变化得到两个电动缸杆长变化曲线,动力学仿真结果与数学模型计算结果如图2和图3所示。
通过对数学建模得到的杆长变化与运动学样机仿真得到的杆长变化对比分析,两电动缸杆长随时间变化曲线基本一致,验证数学模型的正确性;同时将数学模型计算的杆长变化数据,导入到Adams中生成样条曲线,并将数据加载到两个电动缸上,测量两轴变化规律,结果与预先设定的参数完全吻合;通过上面对正反解结果分析,表明二自由度模拟台结构设计无论是从理论上还是应用上都具有可行性,为下一步控制系统设计提供了数学模型。
4 总结
通过对2-DOF运动模拟台的数学模型建立和仿真,该模拟台可实现搭载平台方位俯仰运动,满足机载激光通信APT系统检验对姿态变化的需求,同时由于只有两个自由度,控制系统简单,结构具有轻小型和简便性,方便外场试验。
参考文献
[1]姜会林,佟首峰等,空间激光通信技术与系统[M].北京:国防工业出版社,2010: 5-20.
[2] Bobby.L and Ulich.“Overview ofacquisition, tracking, and pointingsystem technologies”,SPIE, 1988, Vol.887,pp.40-63.
[3]孟立新,张立中,李小明,孙鹤源,李永豪,直升机载高压电力巡线用稳定吊舱设计[J].电力系统自动化,Vol. 36.No.21(2012).
[4]张立中,白杨杨,孟立新,洪进.2-DOF模拟台姿态误差动力学仿真分析[J].长春理工大学学报,2014,37 (05):12-14.
[5]黄真,孔令富,方跃法,并联机器人机构学理论及控制[M].北京:机械工业出版社.1997:25-36.

