福建省交通工程材料价格定价来源相对重要性评价

■李道松

（福建省交通工程造价管理站，福州 350001）

1 引言

当前，交通工程造价站在网上定期发布交通工程材料价格时，其价格的制定主要是参考各定价来源收集到的价格而最终确定出来的。虽然，当前材料价格市场存在波动加剧，以及定价来源不断增多的情况，但往往会发现某个或者几个定价来源对于材料价格的制定与发布参考价值更大。因此，如何更加有效的、高效的利用各个定价来源的数据，如何更加准确的考虑各个定价来源的相对重要性以及制定与发布材料价格，对于提升交通工程造价站的整体服务水平和服务质量都至关重要。

定价来源相对重要性评价是一个典型的自变量相对重要性评价问题，针对该问题，已有许多学者进行了相关研究。张波等[1]提出了一种可视化图示法用于评价线性回归模型中自变量的相对重要性。施庆生等[2]通过偏最小二乘法对影响江苏省房价的九类自变量进行了研究，并利用变量投影重要性计算了各影响变量的重要程度。马金辉等[3]采用优势分析方法对影响白龙江流域泥石流灾害的自变量的相对权重进行了求解。于松青和林盛[4]基于偏最小二乘回归的方法对影响山东省电力需求的自变量进行了重要性分析。杨卫兵等[5]通过Logistic回归模型和决策树模型得出了影响居民环境治理支付意愿的自变量重要性排序。楼狄明等[6]基于偏最小二乘法分析了影响柴油机颗粒物排放特性的自变量的影响强度。Admassu和Jan[7]采用Shapley值法对影响人类主观幸福感的几个因素进行了相对重要性分析。Tso等[8]通过使用互相关分析，对液压断层分析中的影响因素进行了相对重要性的研究。

在传统的多元线性回归模型当中，如果自变量之间互不相关，则有以下三种方法来估计它们的相对重要性：（1）简单相关系数（ryxi）；（2）以斜率为基础的指标如标准回归系数（βi）等；（3）方差降低指标如半偏相关系数（ry(xt|x1…xj)）等[9]。 然而当自变量之间存在相关性时，上述方法的模型依赖性将十分严重。鉴于此，Johnson[10]提出了相对权重估计法用以估计自变量相对重要性。相对权重法需要分别建立原始变量对正交变量以及因变量对正交变量的线性回归方程，其中，自变量的相对重要性即为两组回归系数平方的积和[11-12]。Chao Y E等[13]通过相对权重法对影响公共健康的主要因素的相对重要性进行了分析，结果表明相对权重法比优势度指数法具有计算量更小更稳定的特点。代鲁燕等[14]基于相对权重

法对肝病手术病人预计存活时间的影响因素进行了评价，并指出当自变量间存在相关性时，

采用相对权重法对自变量的相对重要性进行评价，其结果更加科学、稳定，与实际情况更为贴切。

综上所述，相对权重法在对自变量的相对重要性评价中具有很强的适用性，因此本文将其应用到福建省交通工程材料价格的各定价来源相对重要性评价中。

2 相对权重法

（1）相对权重法的基本原理

图1表示的是包含三个自变量的相对重要性示意图[9]。各自变量和因变量之间的关系可以通过两个独立的回归方程进行表示。

以自变量X1为例，通过式（1）描述原始变量Xi和正交变量Zk的关系：

图1 自变量的相对重要性示意图

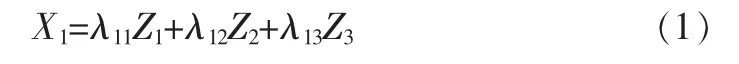
其中，λik为 Xi关于 Zk的回归系数。 通过式（2）描述正交变量Zk和因变量Y之间的关系：

其中，βk为Y关于Zk的回归系数。因此，X1的相对权重 ε1可以通过式（3）求出：

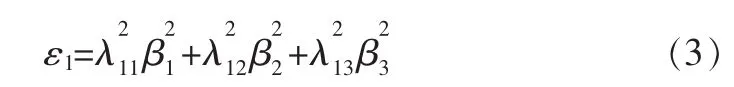
（2）相对权重法的数学原理

假设因变量y为n×1列矩阵，自变量n×p为满秩的阶矩阵，并且所有变量均满足标准化形式，那么，原始变量矩阵X的正交转换如式（4）所示：

其中，P为矩阵XX′的特征向量，Q为矩阵X′X的特征向量。矩阵Z为彼此互不相关但与原始自变量存在高度相关性的正交变量矩阵，通过式（5）可计算出y关于矩阵Z的回归系数β：

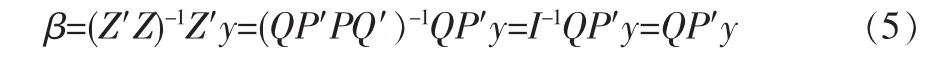
由于正交变量之间不具有相关性，则可以用β2来表示正交变量矩阵Z占因变量y的贡献比例的大小。β2可以大致地表达出原始变量矩阵X中各自变量的相对重要性。为了提高相对重要性求解的精确性，通过式（6）建立原始变量对正交变量的线性回归方程：

由于矩阵Z中的正交变量彼此之间不具有相关性，则可以用 Λ2()来表示正交变量矩阵Z占原始变量矩阵X的贡献比例的大小。因此，各变量的相对权重ε可通过式（7）求出：

因为相对权重是由原始变量经过正交转换而求出的，所以，其可以更好地处理自变量间存在的多重共线性的问题。此外，相对权重法求解出的各个自变量的权重之和与整个模型的决定系数R2相等，如式（8）所示：

因此，相对权重可以表示为各自变量解释因变量变异（方差）的比例，其不仅兼顾了各个自变量的直接效应还考虑了其与回归方程中其他变量进行结合时的效应，以使得各自变量的相对重要性能够被更加直观准确的表达。

3 实证分析

（1）实证背景

为研究福建省交通工程材料价格各个定价来源的相对重要性，以2002～2015年的福建省交通工程造价站发布的数据为基础，钢材材料中的钢板价格 为例，研究福州公路局、福州交通局、TM公司、住建厅造价站、福州物价局、建材在线、网络价格等7个价格定价来源的相对重要性。

（2）结果分析

通过Stata软件首先对钢板价格的各个定价来源进行相关系数分析，各定价来源的相关系数结果如表1所示。

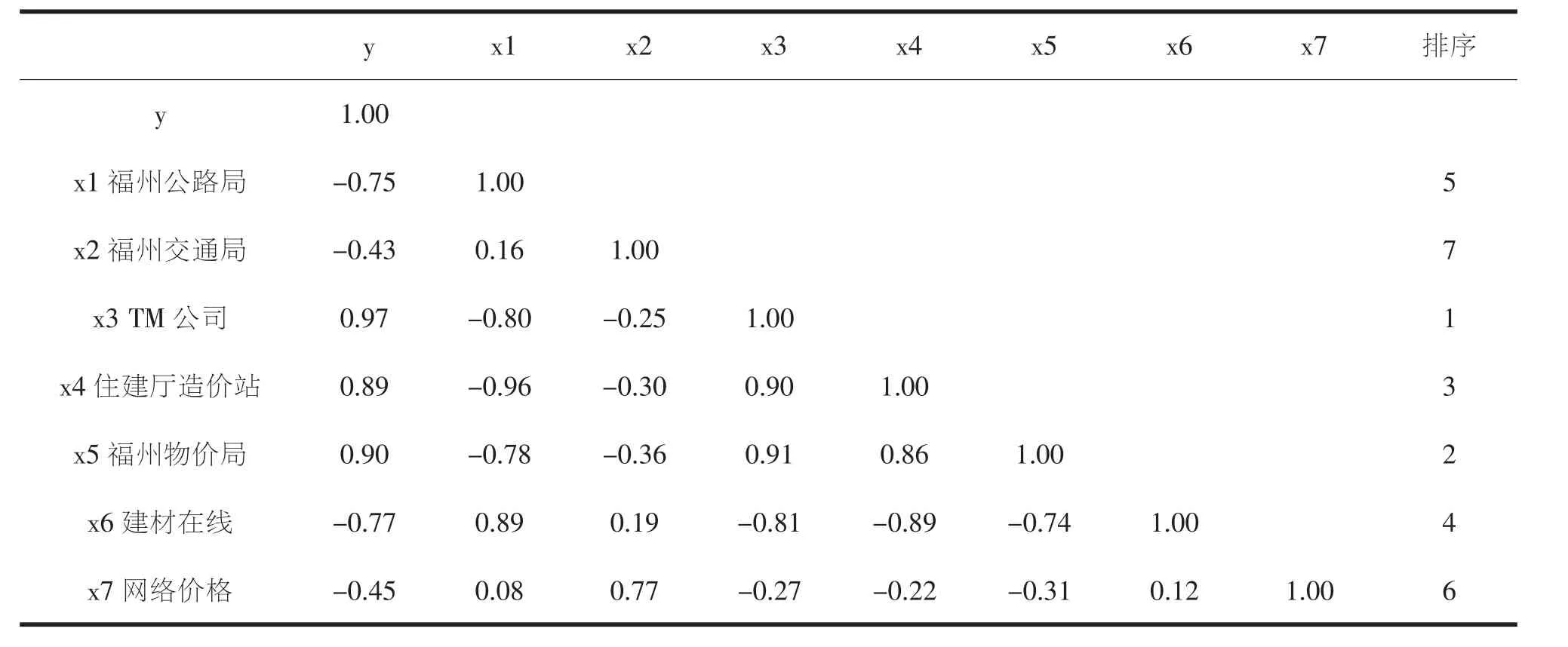
表1 钢板价格定价来源的相关系数结果

从表中可以看出，福建省交通工程造价站发布的价格数据和各个定价来源收集到的数据都存在一定的相关性。其中，TM公司具有的相关系数最大（0.97），然后是福州物价局（0.90）、住建厅造价站（0.89）等。然而，虽然相关系数分析能较准确地确定各个定价来源的相对重要性排序，但是无法精确的表达出对各定价来源的相对重要性程度。而采用相对权重法不但可以对各自变量的重要性排序进行准确估计，更能够对各自变量的相对重要性进行有效地定量估计。因此，下面利用相对权重法来考量各个定价来源对福建省交通工程材料价格的参考权重的大小，结果如表2所示。

在表2中的 同样表示钢板价格 对于各个定价来源的相关系数。此外，相对权重法估计的各定价来源的相对重要性之和等于总模型的 ，也就是表2中的sum_epsilon为0.9927即为总模型的 ，说明了模型拟合程度很高。最后，各定价来源的相对重要性可以表示为其所能解释的因变量的贡献度占已知决定系数 的百分比，因此可以得知TM公司对钢板价格的参考价值最大，相对重要性达到27.2%，接下来依次是福州物价局（19.54%）、住建厅（16.98%）、建材在线（13.12%）、福州公路局（12.09%）、网络价格（6.38%）以及福州交通局（4.69%）。

表2 钢板价格定价来源相对重要性评价结果

通过上述分析可以看出，无论是从传统的相关系数角度出发，还是从相对重要性PropWeights角度出发，各个定价来源对于钢板价格的参考价值的排序是一致的。由此可见，相对权重法不仅可以对各定价来源的相对重要性做出排序，还可以定量地估计各数据定价来源的相对重要性，从而使其相对重要性表达更精确、直观。

本文还分别对交通工程造价站负责制定的其他重要交通工程材料价格进行了定价来源相对重要性分析。其中，钢材类、水泥类、石油类、砂和碎石类定价来源相对重要性结果汇总如表3～表6所示，“-”表示该材料缺少这一定价来源。

表3 钢材类价格定价来源相对重要性评价结果及排序

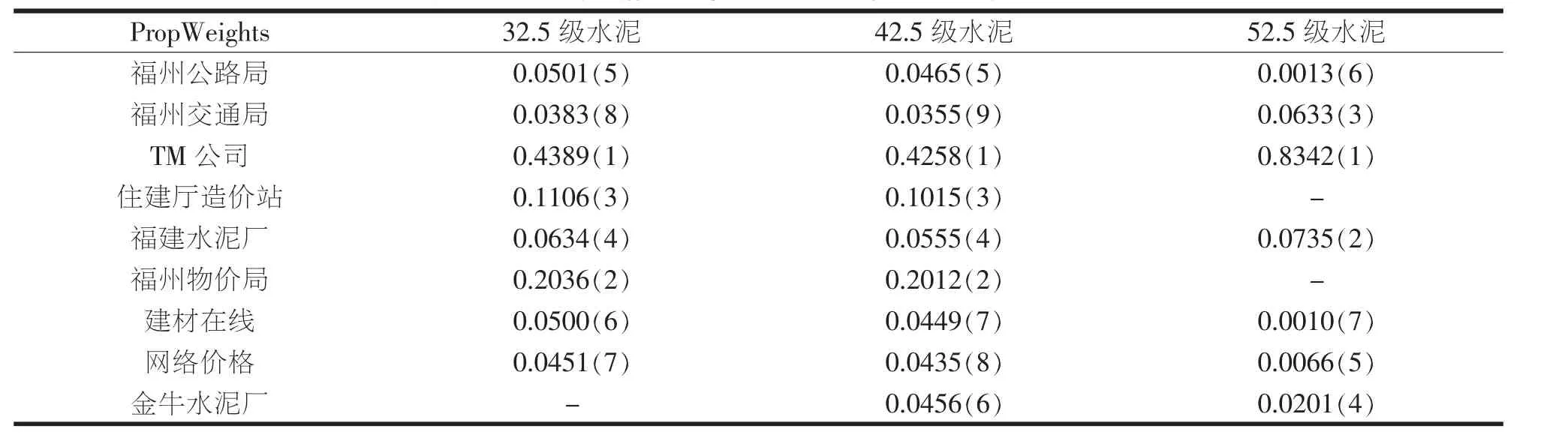
表4 水泥类价格定价来源相对重要性评价结果及排序

表5 石油类价格定价来源相对重要性评价结果及排序

表6 砂和碎石类价格定价来源相对重要性评价结果及排序

根据表3～表6的结果，可以发现相同的定价来源对于不同的交通工程材料价格，其相对重要性的排序和PropWeights往往是有所不同的，所以每一种材料价格的制定都需要进行具体分析。同时，通过观察TM公司的相对重要性排序和PropWeights值，可以发现其往往都排在较为靠前的位置，说明了该渠道的价格数据相对来说最为精确、完整、科学。

4 结论

在市场经济条件下，交通工程造价站是否能对各定价来源进行有效的相对重要性评价，决定了其能否准确、迅速的对各定价来源的参考价值进行科学区分，并制定出最具有实际指导意义的交通工程材料价格。由于相对权重法相比于传统的相关系数分析能更好地求解自变量存在相关性时的相对重要性问题，所以本文将其应用到了福建省交通工程材料价格各定价来源的相对重要性评价当中，证明了该方法的可行性。通过实例研究，得出各定价来源对于钢板价格的相对重要性排序依次是TM公司、福州物价局、住建厅、建材在线、福州公路局、网络价格以及福州交通局；而其他材料价格的定价来源相对重要性评价结果则各有不同。总体来说，TM公司的影响作用较强，在交通工程造价站今后制定交通工程材料价格时，可重点参考TM公司的价格数据。

[1]张波,黄启风,代鲁燕,等.Logistic回归模型中自变量的秩优势比图[J].统计与决策,2008（24）:87-89.

[2]施庆生,翟文斌,邓晓卫.基于PLS的江苏省房地产价格影响因素的实证研究[J].数学的实践与认识,2013,43（17）:19-26.

[3]马金辉,田菲,陈璐.基于优势分析法的泥石流影响因子相对重要性分析——以白龙江流域为例[J].兰州大学学报（自然科学版）,2014,50（5）:722-727.

[4]于松青,林盛.基于偏最小二乘回归的山东省电力需求预测分析[J].干旱区资源与环境,2015,29（2）:14-20.

[5]杨卫兵,丰景春,张可.农村居民水环境治理支付意愿及影响因素研究——基于江苏省的问卷调查[J].中南财经政法大学学报,2015（4）:58-65.

[6]楼狄明,胡磬遥,胡志远,等.基于PLS的喷油参数对共轨柴油机颗粒物排放特性影响研究[J].内燃机工程,2015,36（5）:56-62.

[7]Admassu N L,Jan A O.The Relative Importance of Health,Income and Social Relations for Subjective Well-being:An Integrative Analysis[J].Social Science&Medicine,2016,152:176-185.

[8]Tso M,Zha Y Y,Yeh J,et al.The Relative Importance of Head,Flux,and Prior Information in Hydraulic Tomography Analysis[J].Water Resources Research,2016,52（1）:3-20.

[9]Johnson J W,Lebreton J M.History and Use of Relative Importance Indicesin OrganizationalResearch [J].OrganizationalResearch Methods,2004,7（3）:238-257.

[10]Johnson J W.A Heuristic Method for Estimating the Relative Weight of Predictor Variables in Multiple Regression[J].Multivariate Behavioral Research,2000,35（5）:1-19.

[11]James M.Multivariate Relative Importance:Extending Relative Weight Analysis to Multivariate Criterion Spaces[J].Journal of Applied Psychology,2008,93（2）:329-345.

[12]Johnson J W.Determining the Statistical Significance of Relative Weights[J].Psychological Methods,2009,4（1）:387-399.

[13]Chao Y E,Zhao Y,Kupper L L,et al.Quantifying the Relative Importance of Predictors in Multiple Linear Regression Analyses for Public Health Studies[J].Journal of Occupational and Environmental Hygiene,2008,5（8）:519-529.

[14]代鲁燕,沈其君,张波.相对权重法在线性模型自变量相对重要性中的估计及其应用[J].中国卫生统计,2013,30（1）:19-22.