磁性硅烯超晶格中电场调制的谷极化和自旋极化∗
侯海燕1) 姚慧1) 李志坚1)2) 聂一行1)2)
1)(山西大学理论物理研究所,量子光学与光量子器件国家重点实验室,太原 030006)
2)(山西大学极端光学协同创新中心,太原 030006)(2018年1月11日收到;2018年2月2日收到修改稿)
1 引 言
自实验室成功制备硅烯以来[1,2],其理论和实验研究引起了人们极大的兴趣[3,4].硅烯的晶体结构是由单层硅原子合成的二维蜂窝状,与石墨烯的六角蜂窝状结构十分类似,且硅与合成石墨烯的碳又为同主族元素,因此硅烯几乎具有石墨烯所有的物理性质和量子现象.但与石墨烯相比,硅烯的晶体结构为非共面的翘曲结构,这使得硅烯还具备许多优于石墨烯的物理性能.例如,硅烯具有较强的自旋轨道耦合能和外场可调的能隙[5],在硅烯系统中通过外电场的调节可以实现能带绝缘体和拓扑绝缘体之间的拓扑相变[6]及各种量子自旋霍尔效应[7]等.另外,硅烯更容易与硅基半导体电子技术相结合[8].
在二维六角晶格材料中,电子除了电荷和自旋自由度外,还具有谷自由度[9]和晶格赝自旋自由度[10].所谓谷就是能谷,即固体材料中能带结构的极值点.在硅烯中,谷为六角布里渊区K和K′点处两个不等价的狄拉克锥,与石墨烯中谷的定义类似.与电子的自旋自由度类似,也可以利用电子的谷自由度作为信息载体,通过对谷自由度的调控进行信息处理、设计相关的谷电子功能器件、实现量子计算和量子通讯[11,12]等.对电子谷自由度的相关研究称为谷电子学[9,13].赝自旋实际上起源于二维六角结构中的两种子晶格,赝自旋的极化代表电子在A子晶格中运动或B子晶格中运动[14].
自超晶格的概念提出以来,其结构在控制二维半导体中电流的输运性能方面表现得非常成功[15−19].目前,有关石墨烯超晶格的理论研究已经非常成熟[15],且实验室已经成功合成石墨烯超晶格[16].然而,鲜有关于硅烯超晶格中的电子、自旋、谷和赝自旋的输运性质以及极化调控的理论和实验研究[17−19].最近,理论预言可以利用磁性超晶格的相关参数调控热电输运性质,提高自旋依赖和谷依赖的塞贝克系数[20].文献[21]利用磁矢势在硅烯上形成磁超晶格,研究了其中的自旋和谷输运性质,以及自旋-谷退耦合机理.本文考虑一个磁性硅烯超晶格系统,研究了交换场、化学势和外加电场对谷极化、自旋极化以及赝自旋极化输运的影响.结果表明,在超晶格中可以通过调控电场实现谷极化、自旋极化以及赝自旋极化,只要超晶格中的晶格数超过10,就可以实现完全极化,并且通过改变电场的方向和大小实现极化翻转.
2 哈密顿量及计算
如图1所示,本文研究的模型是处于x-y平面的一个具有周期性磁场调制的二维硅烯超晶格,该模型可以看作由长度为L的磁性硅烯区域和长度为D的正常硅烯区域依次排列,最后连接两个半无限的正常硅烯电极.假设硅烯超晶格有N个周期,则超晶格中共有N个磁性硅烯区域、(N−1)个正常硅烯区域和两个半无限的正常硅烯电极.图1中h1和h2为硅烯片上表面和下表面的磁性绝缘膜,EZ为外电场.
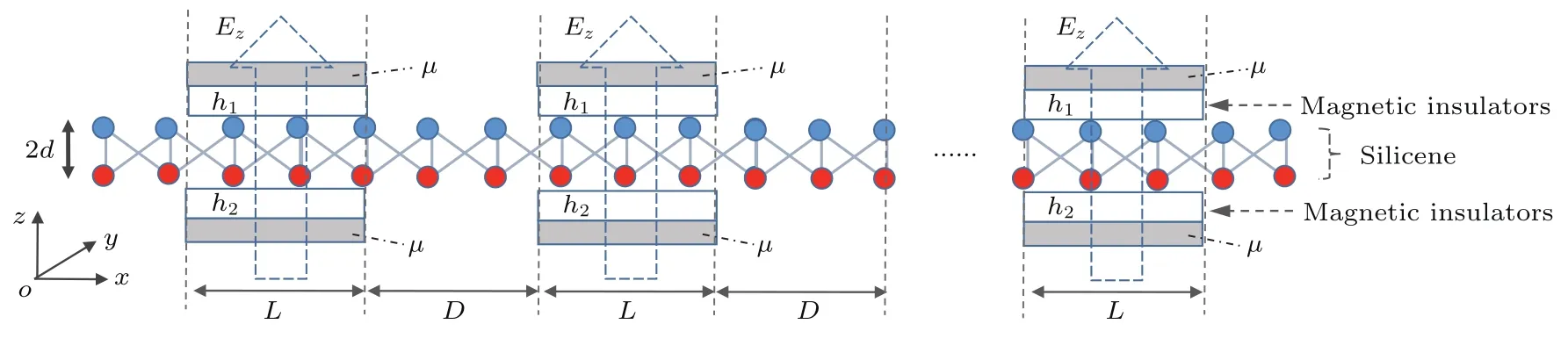
图1 磁性硅烯超晶格的示意图Fig.1.Schematic diagram of a magnetic silicene superlattice.
硅烯超晶格中电子的低能有效哈密顿量可以表示为[5,7,22−24]
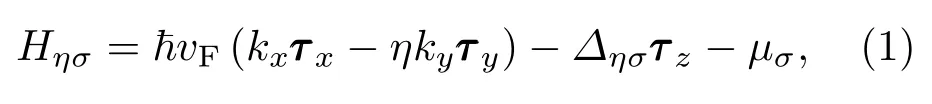
式中µσ=µ+δσhF为自旋依赖的化学势,µ为由门电压引起的化学势,δ↑(↓)=±1对应于自旋向上(向下);kx和ky分别为超晶格中电子的动量波矢在x轴和y轴的分量;τ x,τ y和τ z为晶格赝自旋空间中的泡利矩阵;~为普朗克常数;vF≈5.5×105m/s为狄拉克点附近电子的费米速度;∆ησ=ηδσ∆SO−∆Z+δσhAF,其中∆SO为硅烯固有的自旋-轨道耦合能,∆Z=edEZ为垂直于硅烯片的外电场在A和B子格之间诱导的电势差,可通过外电场EZ进行调控,2d为A和B子格所在平面的垂直间隔距离;η=±1对应于K谷和K′谷;hF/hAF为超晶格中磁性区域的铁磁/反铁磁交换场,其中磁性区域的磁交换场由位于硅烯片上表面和下表面磁性绝缘膜的近邻效应所引起[25],而磁性区域的铁磁/反铁磁性由磁性绝缘膜的磁化方向平行/反平行决定.在正常硅烯区域,∆Z=hF=hAF=µ=0;在铁磁区,hF̸=0,hAF=0;对于反铁磁情况,hF=0,hAF̸=0.
在正常区域和磁性区域哈密顿量的能量本征值分别为:
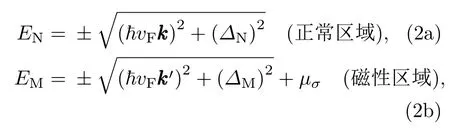
式中∆N=ηδσ∆SO为正常区的能隙,∆M=ηδσ∆SO−∆Z+δσhAF为磁性区的能隙,二者都依赖于自旋和谷.如果类比于相对论性的质量,∆M等价于硅烯超晶格中电子在磁性区的自旋和谷依赖的狄拉克质量[24],而且此质量可以通过电场和交换场调控.分别为正常区域和磁性区域的动量波矢.设定x轴垂直于分界面且电子沿x轴方向运动,在y轴方向上电子的动量保持不变.当左侧电极注入能量为E、谷和自旋分别为η和σ的电子时,电子经中间区域透射到右侧电极,根据狄拉克方程HησΨ=EΨ,可以得到左侧电极、中间磁性区域、中间正常区域和右侧电极中电子的波函数的矩阵形式分别为:

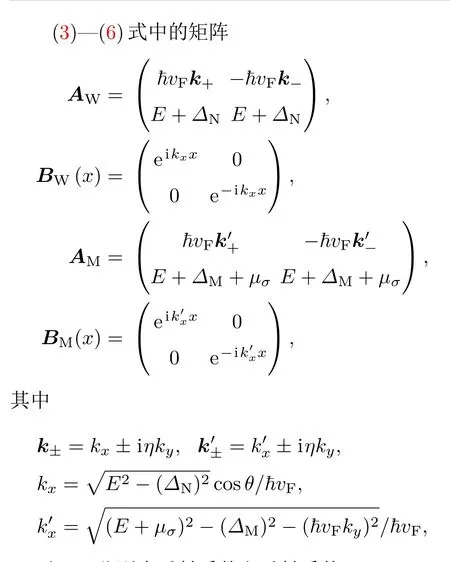
rησ和tησ分别为反射系数和透射系数.
波函数在分界面处的连续性给出
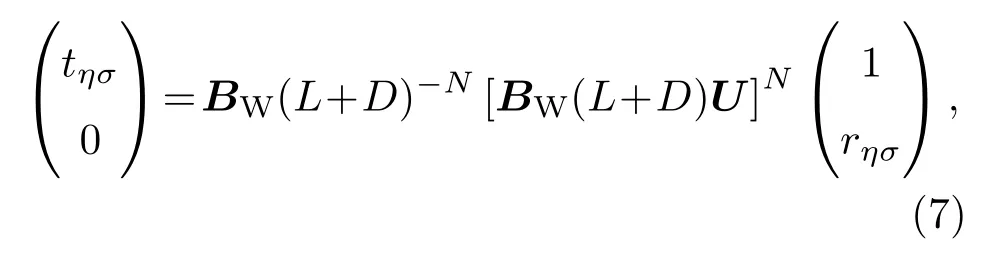
根据Landauer-Buttier公式并考虑各种可能的入射方向,谷自由度为η、自旋为σ的电子在零温下的输运电导Gησ可以表示为:
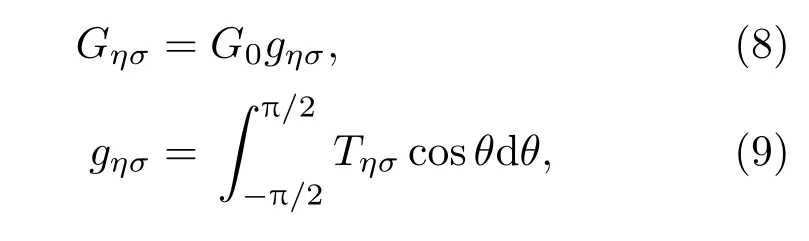
式中θ为电子的入射方向与x轴之间的夹角;为单位电导,gησ为无量纲的电导,W为硅烯片的宽度,kF为费米波矢.利用(9)式,可以定义谷电导和自旋依赖的电导于是谷极化率PV和自旋极化率PS分别定义为:
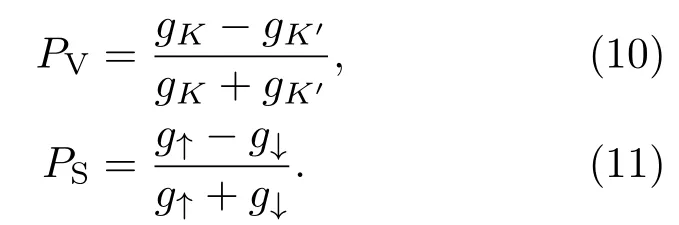
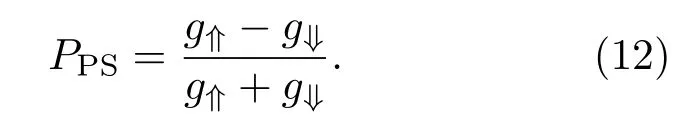
借助于(12)式可以描述赝自旋极化的量子输运.
3 数值结果与分析
3.1 静电势超晶格
首先考虑硅烯超晶格中hF=hAF=0的情况,只有电场EZ存在,即超晶格是由垂直于晶格平面的N个电场区和N-1个无场区组成.硅烯中的自旋轨道耦合能[3,6]∆SO=3.9 meV,设L=D=50 nm.当hF=hAF=0时,不存在自旋极化和谷极化的情况.但是,如果电子入射能量取为E=4 meV,由于E→∆SO,晶格赝自旋是极化的.图2给出了对于几种不同的晶格数,赝自旋极化的电导和赝自旋极化率对电势差∆Z的依赖.在图2(a)中赝自旋极化的电导劈裂成两个峰,这是由于对于给定的∆Z,A和B两个子晶格中的电子感受的静电势不同,于是当电子隧穿超晶格时,共振隧穿发生在不同的∆Z(势能)处.共振峰的位置由dgησ/d∆Z=0决定,即对于赝自旋⇑(⇓),赝自旋极化的电导峰位于∆Z∼µ(−µ)附近,两个峰关于∆Z=0是对称的,赝自旋极化的电导峰劈裂宽度为2µ.随着晶格数增加(N=1,N=2,N=5,N=10),类似于多光束干涉,赝自旋极化的电导峰变得越来越尖锐,使赝自旋极化的电导的峰完全分开.硅烯超晶格的这种透射性质可以用于赝自旋选择器,通过调节外电场EZ选择透射出来的赝自旋.赝自旋极化率PPS随电势差∆Z的变化如图2(b)所示,超晶格的输运特性使得赝自旋极化在零场处发生翻转,晶格数越多翻转越明显,而且在零场两侧附近很宽的范围内赝自旋是完全极化的.
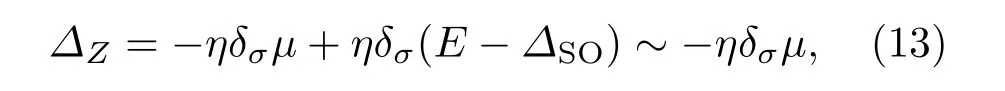
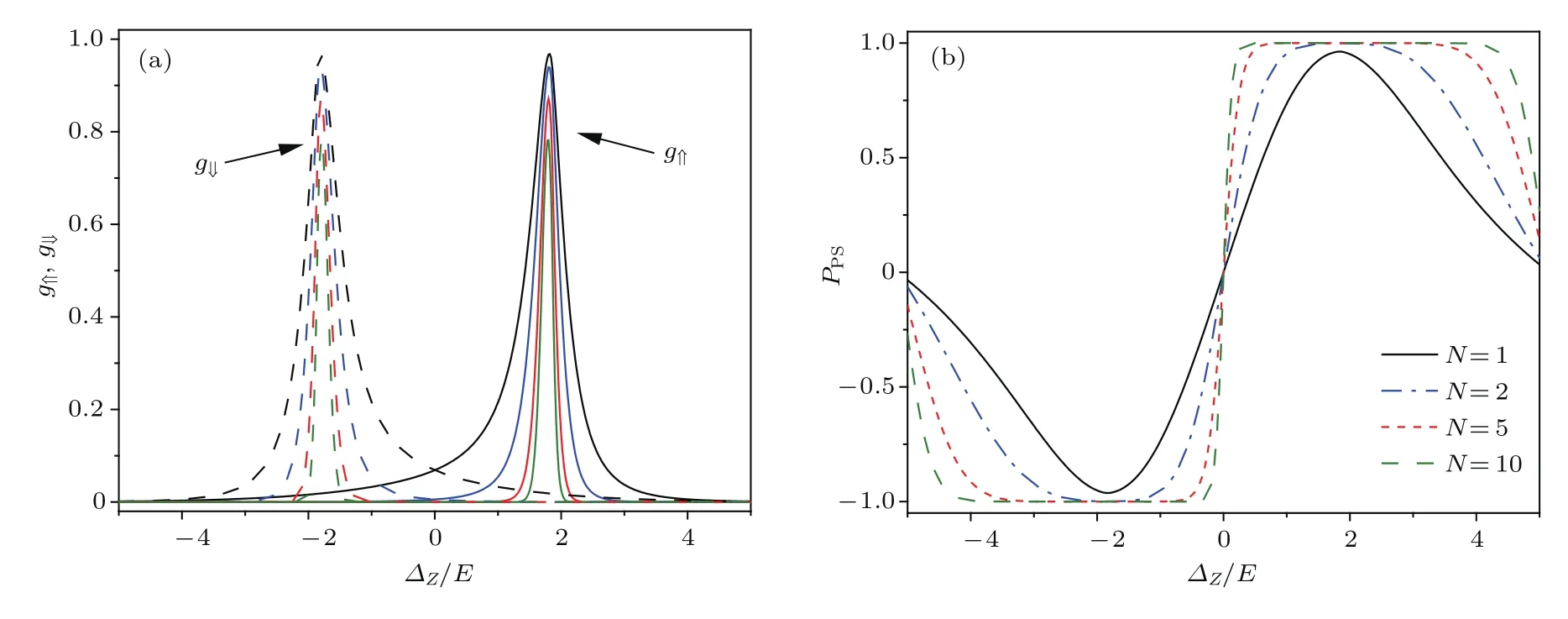
图2 (a)赝自旋极化电导g⇑(实线)和g⇓(虚线)随电势差∆Z的变化关系;(b)赝自旋极化率PPS随电势差∆Z的变化关系.参数选取∆SO/E=0.975,L/l=0.53,µ/E=1.8,hF/E=hAF/E=0Fig.2.(a)Pseudospin polarized conductance g⇑ (solid line)and g⇓ (dashed line);(b)pseudospin polarization PPS as a function of the on-site potential dif f erence∆Z.Parameters are∆SO/E=0.975,L/l=0.53,µ/E=1.8,hF/E=hAF/E=0.
3.2 铁磁硅烯超晶格
对于铁磁硅烯超晶格,即hF̸=0,hAF=0.磁场的存在不仅可使自旋依赖的电导峰劈裂,也可以使谷电导劈裂.图3给出了hF/E=1.25,hAF/E=0,µ/E=0时,谷电导以及谷极化率随电势差∆Z的变化(此时不存在自旋极化和赝自旋极化).谷电导是由自旋向上和自旋向下的电子电导组成的,于是磁场的存在也可以使谷电导劈裂,如图3(a)所示.此时谷电导峰的位置由
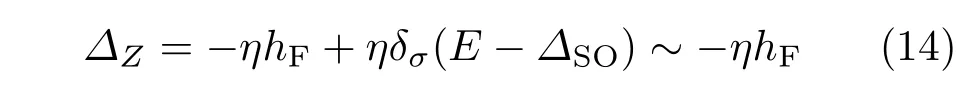
决定.谷电导峰关于∆Z=0也是对称的,劈裂的宽度为2hF,而且随着晶格数增加,谷电导峰变得越来越尖锐,谷电导gK和gK′的峰完全分开.这种透射性质可以用于选择电子的谷自由度,即基于磁性硅烯超晶格通过调节外电场EZ选择透射出来的电子的谷自由度.谷极化率PV随电势差∆Z的变化如图3(b)所示,随着晶格数增加,谷极化率接近100%,这是由于超晶格增强了谷电导的共振透射特性.从图3(a)可以发现,随着晶格数增加,gK和gK′的峰重叠范围越来越小,当晶格数达到10时,gK和gK′的峰在∆Z=0附近已经完全分开,不再重叠.因此在零场两侧谷自由度完全极化,即在零场两侧谷极化率PV=±1.如果用谷自由度存储信息,这种谷极化率随着外场电场反向而翻转的特性非常有利于信息的存储与读取.
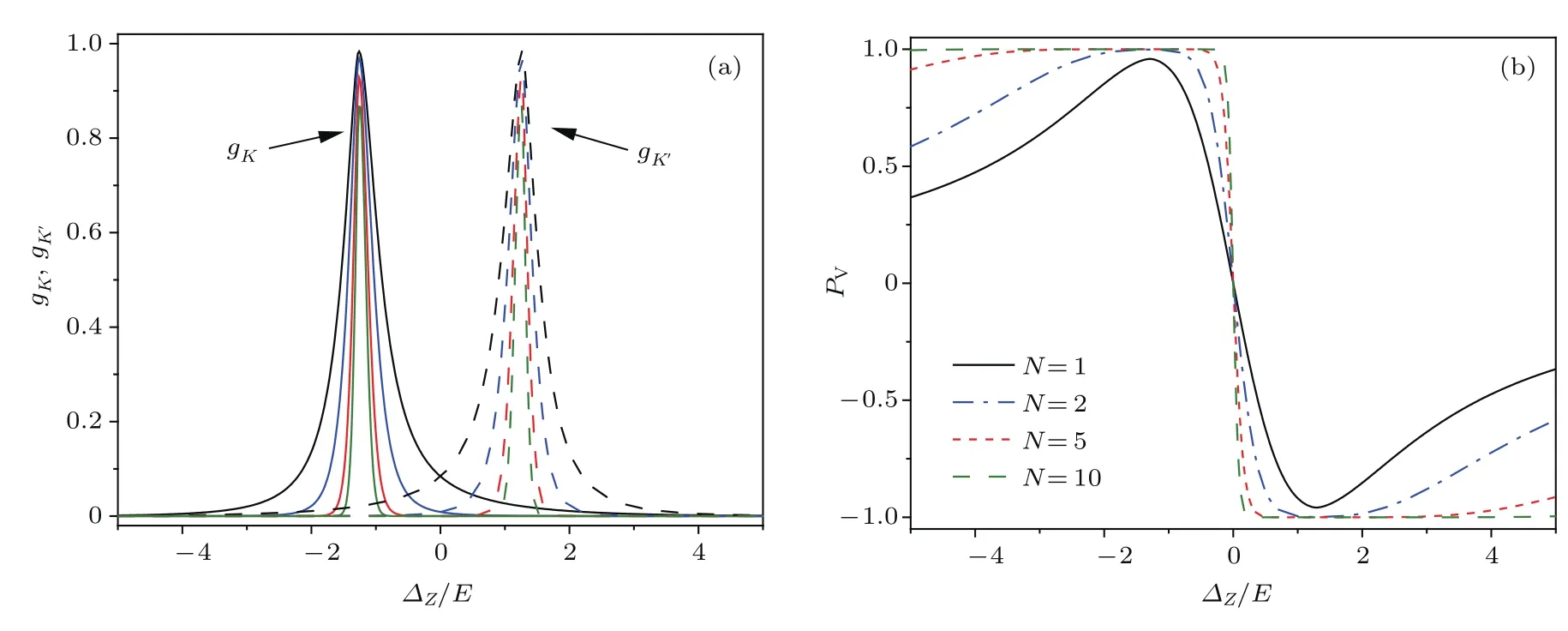
图3 (a)谷电导gK(实线)和gK′(虚线)随电势差∆Z的变化;(b)谷极化率PV随电势差∆Z的变化;参数µ/E=0,hF/E=1.25,hAF/E=0,其他参数与图2中的相同Fig.3.(a)Valley conductance gK(solid line)and gK′(dashed line);(b)valley polarization PVas a function of the on-site potential dif f erence∆Z.Parameters areµ/E=0,hF/E=1.25,hAF/E=0,other parameters are the same as in Fig.2.
谷电导实际上来自同一谷中不同自旋电子的贡献.当磁性超晶格中磁场和化学势同时存在时,即hF̸=0,µ̸=0时,电导gησ的峰位于
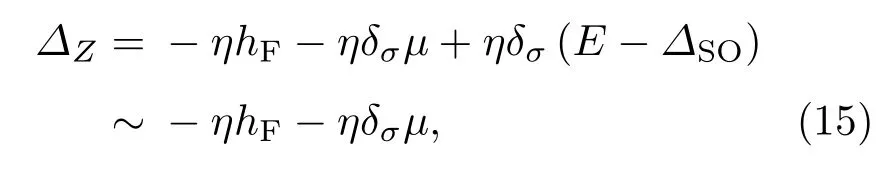
可见电导峰的位置不仅是谷依赖的,而且是自旋依赖的.因此,不仅谷电导gK与gK′分裂开,而且同一谷中的电导也会劈裂为两个峰.gK的两个峰位于∆Z∼−hF−µ(K谷中自旋↑的电子的贡献)和∆Z∼−hF+µ(K谷中自旋↓的电子的贡献);gK′的两个峰位于∆Z∼hF+µ(K′谷中自旋↑的电子的贡献)和∆Z∼hF−µ(K′谷中自旋↓的电子的贡献).图4给出了hF/E=1.25,hAF/E=0,µ/E=2.5时,谷电导和自旋依赖的电导随电势差∆Z的变化.在图4(a)中,实线和虚线分别代表K和K′谷电导,每一类谷电导中包含相距2µ的两个峰.随着晶格数的增加,这些电导峰变得越来越尖锐.图4(b)为谷极化率PV随电势差∆Z的变化,随着晶格数的增加,谷极化增强,当晶格数达到10时,谷极化率可以达到100%.由于µ̸=0,谷电导劈裂为双峰结构,而且只要µ̸=hF,两种谷电导峰就不会重合,结果当∆Z从负到正逐渐增加时,谷极化率发生3次翻转,其极化的顺序为K→K′→K→K′.
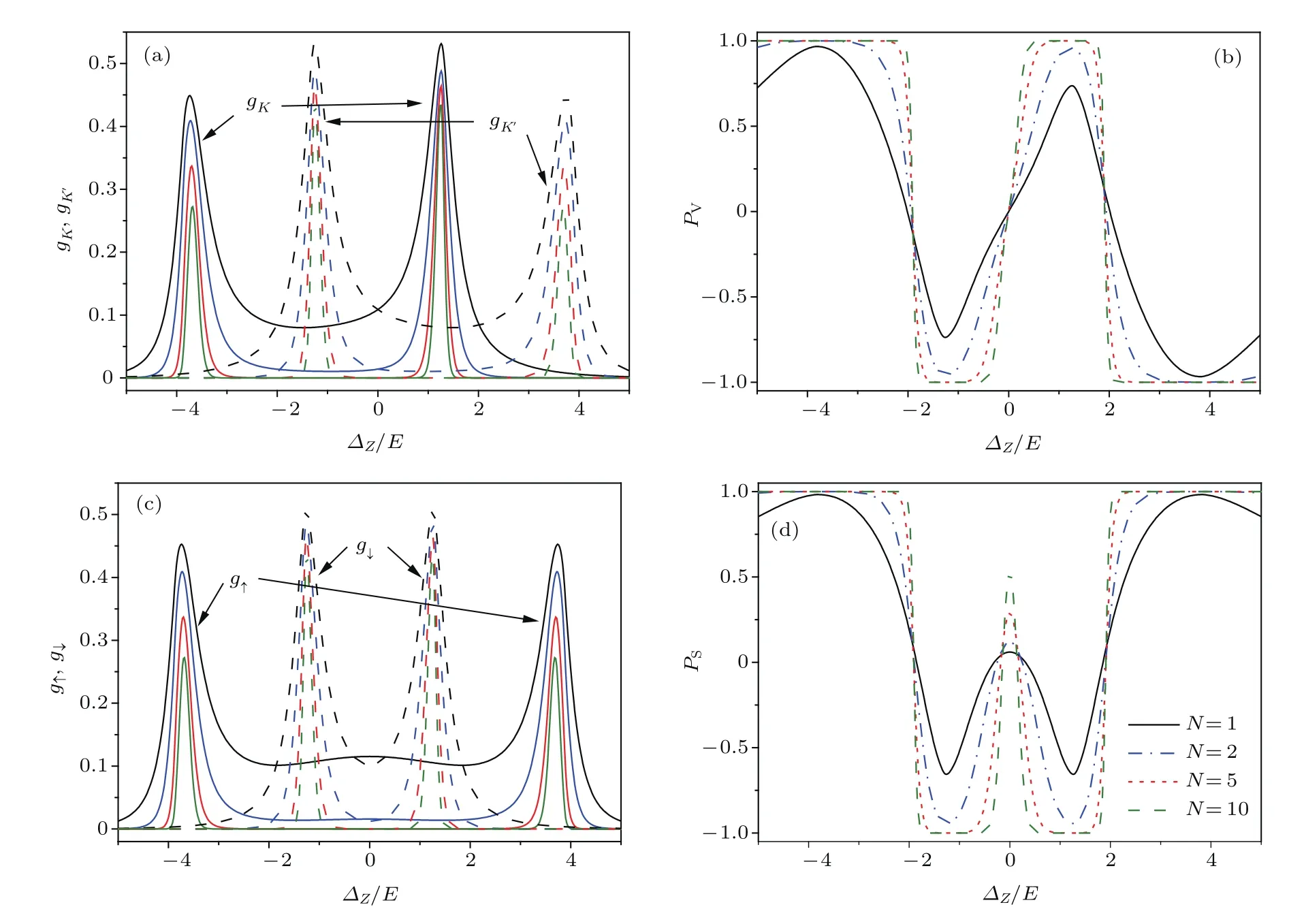
图4 (a)谷电导gK(实线)和gK′(虚线)和 (c)自旋依赖电导g↑(实线)和g↓(虚线)随电势差∆Z的变化;(b)谷极化率PV和(d)自旋极化率PS随电势差∆Z的变化;参数µ/E=2.5,hF/E=1.25,hAF/E=0,其他参数与图2中的相同Fig.4.(a)Valley conductance gK(solid line)and gK′(dashed line)and(c)spin resolved conductance g↑(solid line)and g↓(dashed line)as a function of the on-site potential dif f erence∆Z;(b)Valley polarization PVand(d)spin polarization PSas a function of the on-site potential dif f erence∆Z.Parameters areµ/E=2.5,hF/E=1.25,hAF/E=0,other parameters are the same as in Fig.2.
自旋依赖的电导来自不同谷中自旋相同电子的贡献.从(15)式可以发现,自旋依赖的电导也有两个峰,而且关于零场对称,g↑的两个峰位于∆Z∼−hF−µ(K谷中自旋↑的电子的贡献)和∆Z∼hF+µ(K′谷中自旋↑的电子的贡献);g↓的两个峰位于∆Z∼−hF+µ(K谷中自旋↓的电子的贡献)和∆Z∼hF−µ(K′谷中自旋↓的电子的贡献).图4(c)中,实线和虚线分别代表自旋↑和↓的电导.自旋↑的两个自旋依赖电导峰间距为2|hF+µ|,自旋↓的两个自旋依赖电导峰间距为2|µ−hF|,而且它们关于∆Z=0都是对称的.图4(d)是自旋极化率随电势差∆Z的变化,对于10个周期的铁磁硅烯超晶格,很容易达到100%的自旋极化,随着∆Z从负到正的逐渐增加,自旋极化率发生4次翻转,其极化的顺序为↑→↓→↑→↓→↑.
3.3 反铁磁硅烯超晶格
当磁性区的两个磁场方向相反时,即hF=0,hAF̸=0,称为反铁磁硅烯超晶格.在这种情况下,K谷电导峰与K′谷电导峰重合,没有谷极化,但输运电子的自旋是极化的.图5给出了hF/E=0,hAF/E=1.25,µ/E=0时,自旋依赖的电导以及自旋极化率随电势差∆Z的变化.自旋依赖的电导只有一个峰,其位置由
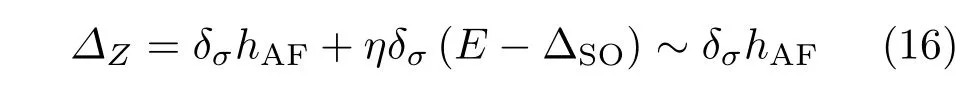
决定,g↑和g↓的峰距为2hAF,如图5(a)所示.反铁磁硅烯超晶格中自旋依赖电导峰的劈裂,是由电子在铁磁区的类狄拉克质量∆M中自旋依赖的δσhAF项引起的.随着晶格数的增加,自旋极化更加完美,图5(b)给出了自旋极化率随电势差∆Z的变化,当晶格数N=10时,零场两边PS=±1.
当hAF̸=0,µ̸=0时,反铁磁硅烯超晶格中可以同时出现自旋极化和谷极化,而且自旋依赖的电导和谷电导都劈裂为双峰结构,峰的位置由
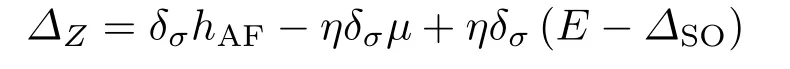

决定.图6给出了hF/E=0,hAF/E=1.25,µ/E=2.5时,自旋依赖的电导和谷电导以及自旋极化率和谷极化率随电势差∆Z的变化.图6(a)为自旋依赖的电导随电势差∆Z的变化,g↑的两个峰位于∆Z∼hAF−µ(K谷中自旋↑的电子的贡献)和∆Z∼hAF+µ(K′谷中自旋↑的电子的贡献);g↓的两个峰位于∆Z∼−hAF+µ(K谷中自旋↓的电子的贡献)和∆Z∼−hAF−µ(K′谷中自旋↓的电子的贡献).当晶格数达到10时,g↑和g↓的峰已经完全分开,因此当电势差∆Z从负到正逐渐增加时,自旋极化率可以发生3次翻转,如图6(b)所示,自旋极化的顺序为↓→↑→↓→↑.
反铁磁硅烯超晶格中谷极化的情况与铁磁硅烯超晶格中自旋极化类似,除了gK与gK′分裂开,同一谷中的电导也会对称地分裂为两个峰.如图6(c)所示,gK的两个峰位于∆Z∼hAF−µ(K谷中自旋↑的电子的贡献)和∆Z∼−hAF+µ(K谷中自旋↓的电子的贡献);gK′的两个峰位于∆Z∼hAF+µ(K′谷中自旋↑的电子的贡献)和∆Z∼−hAF−µ(K′谷中自旋↓的电子的贡献).超晶格的干涉特性可以使这些电导峰完全分开,从而使谷极化率达到100%(见图6(d)).当电势差∆Z从负到正逐渐增加时,谷极化率经过两次翻转,其极化的顺序为K′→K→K′,与铁磁半导体超晶格的情况完全不同.
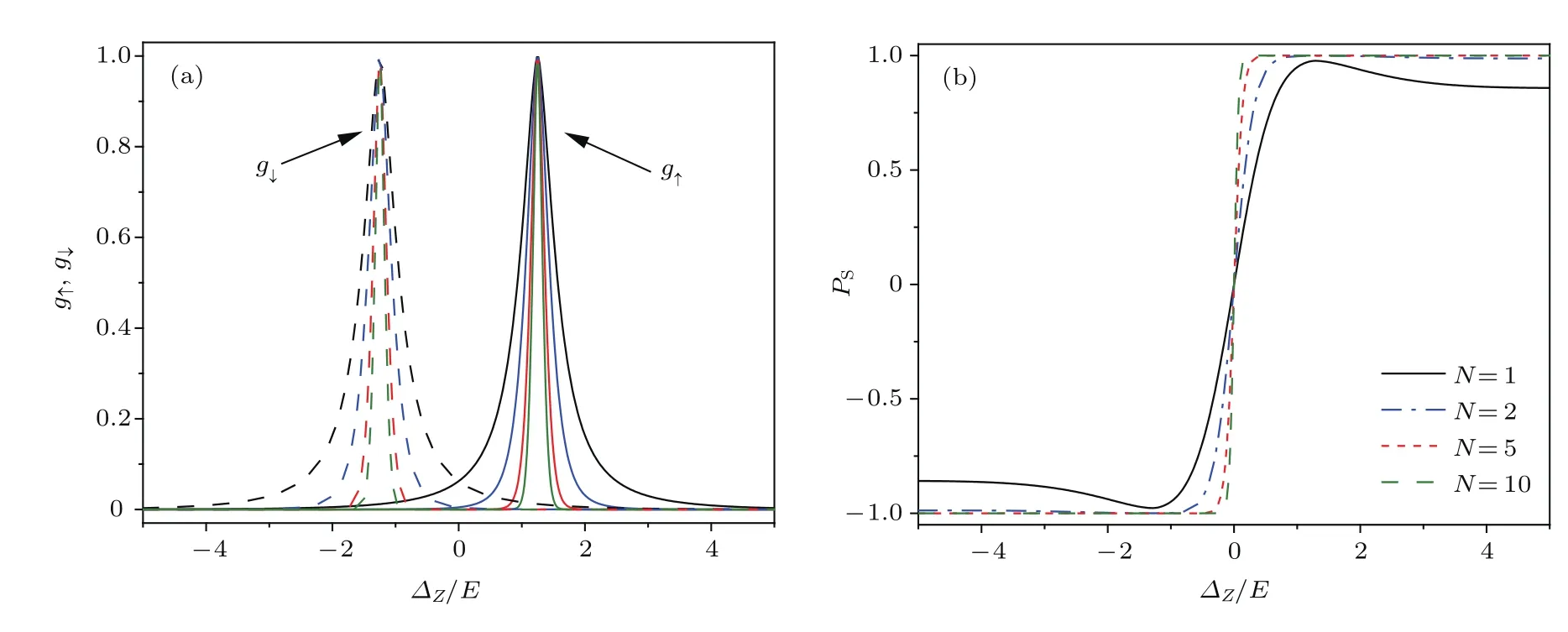
图5 (a)自旋依赖电导g↑(实线)和g↓(虚线)随电势差∆Z的变化;(b)自旋极化率PS随电势差∆Z的变化.参数µ/E=0,hF/E=0,hAF/E=1.25,其他参数与图2中的相同Fig.5.(a)Spin resolved conductance g↑ (solid line)and g↓ (dashed line)and(b)spin polarization PSas a function of the on-site potential dif f erence∆Z.Parameters areµ/E=0,hF/E=0,hAF/E=1.25,other parameters are the same as in Fig.2.
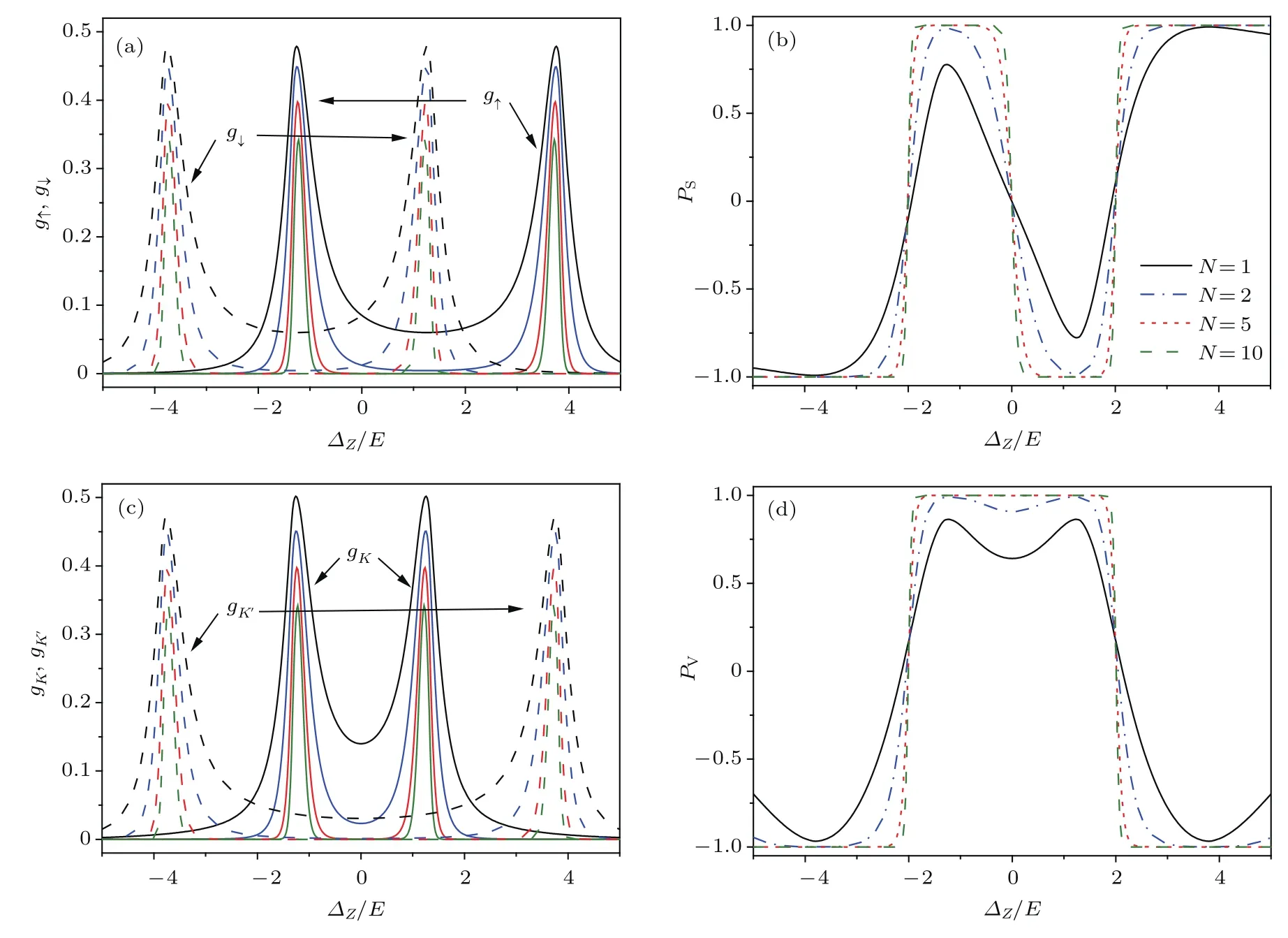
图6 (a)自旋依赖电导g↑(实线)和g↓(虚线)和(c)谷电导gK(实线)和gK′(虚线)随电势差∆Z的变化;(b)自旋极化率PS和(d)谷极化率PV随电势差∆Z的变化;参数µ/E=2.5,hF/E=0,hAF/E=1.25,其他参数与图2中的相同Fig.6.(a)Spin resolved conductance g↑ (solid line)and g↓ (dashed line)and(c)valley conductance gK(solid line)and gK′(dashed line)as a function of the on-site potential dif f erence∆Z;(b)spin polarization PSand(d)valley polarization PVas a function of the on-site potential dif f erence∆Z.Parameters areµ/E=2.5,hF/E=0,hAF/E=1.25,other parameters are the same as in Fig.2.
4 结 论
研究了3种硅烯超晶格中谷极化、自旋极化以及赝自旋极化的输运性质,分析了基于硅烯超晶格的电场调控机理与优势.铁磁硅烯超晶格会导致磁性区的化学势依赖于铁磁交换场,而反铁磁硅烯超晶格中磁性区电子的类狄拉克质量依赖于反铁磁交换场和自旋.本文考虑了入射电子能量接近于自旋轨道耦合能(硅烯的固有能隙)的情况下,外电场对3种极化的调控.对于静电势超晶格,只有赝自旋极化,不存在自旋极化和谷极化,赝自旋⇑和⇓的电导峰完全分开,赝自旋极化率在零场附近发生从−1到+1的翻转,在零场两侧附近很宽的范围内赝自旋是完全极化的.对于铁磁硅烯超晶格,铁磁交换场和化学势导致谷极化和自旋极化同时存在,而且谷电导和自旋依赖的电导随电势差变化出现4个峰.不仅K谷和K′谷的电导峰完全分开,而且每一个谷电导又劈裂为自旋依赖的两个峰.类似地,不仅自旋↑和↓的电导峰完全分开,而且每一种电导峰又劈裂成谷依赖的两个峰.通过调节外电场可以实现谷极化率(或自旋极化率)从−1到+1的翻转.当电势差从负到正逐渐变化时,谷极化的顺序是K→K′→K→K′,自旋极化的顺序是↑→↓→↑→↓→↑.对于反铁磁硅烯超晶格,反铁磁交换场和化学势也可以导致谷极化和自旋极化,谷电导和自旋依赖的电导类似于铁磁硅烯超晶格,也都劈裂成4个峰,而且通过调节外电场也可以实现谷极化率(或自旋极化率)从−1到+1的翻转.但是,当电势差从负到正逐渐变化时,谷极化和自旋极化的顺序与铁磁硅烯超晶格不同,谷极化的顺序是K′→K→K′,自旋极化的顺序是↓→↑→↓→↑.硅烯超晶格使自旋极化、谷极化以及赝自旋极化很容易达到100%,而且利用外加电场就可以操控极化的翻转,这为硅烯在信息存储与读取方面提供了十分有利的条件.
[1]de Padova P,Quaresima C,Ottaviani C,Sheverdyaeva P M,Moras P,Carbone C,Topwal D,Olivieri B,Kara A,Oughaddou H,Aufray B,Lay G L 2010Appl.Phys.Lett.96 261905
[2]VogtP,dePadova P,Quaresima C,Avila J,Frantzeskakis E,Asensio M C,Resta A,Ealet B,Lay G L 2012Phys.Rev.Lett.108 155501
[3]Liu C C,Jiang H,Yao Y 2011Phys.Rev.B84 195430
[4]Chen L,Liu C C,Feng B,He X,Cheng P,Ding Z,Meng S,Yao Y,Wu K 2012Phys.Rev.Lett.109 056804
[5]Ezawa M 2012New J.Phys.14 033003
[6]Ezawa M 2012Phys.Rev.Lett.109 055502
[7]Ezawa M 2013Phys.Rev.B87 155415
[8]Fleurence A,Friedlein R,Ozaki T,Kawai H,Wang Y,Yamada-Takamura Y 2012Phys.Rev.Lett.108 245501
[9]Rycerz A,Tworzydo J,Beenakker C 2007Nat.Phys.3 172
[10]Xu X D,Yao W,Xiao D,Heinz T F 2014Nat.Phys.10 343
[11]Tikhonenko F V,Horsell D W,Gorbachev R V,Savchenko A K 2008Phys.Rev.Lett.100 056802
[12]Wu G Y,Lue N Y,Chen Y C 2013Phys.Rev.B88 125422
[13]Castro Neto A H,Guinea F,Peres N M R,Novoselov K S,Geim A K 2009Rev.Mod.Phys.81 109
[14]Chantngarm P,Yamada K,Soodchomshom B 2016Superlattices and Microstructures94 13
[15]Pham C H,Nguyen V L 2015J.Phys:Condens.Matter27 095302
[16]Meyer J C,Girit C O,Crommie M F,Zettl A 2008Appl.Phys.Lett.92 123110
[17]Zhang Q,Chen K S,Li J 2016Sci.Rep.6 33701
[18]Missault N,Vasilopoulos P,Vargiamidis V,Peeters F M,Duppen B V 2015Phys.Rev.B92 195423
[19]Missault N,Vasilopoulos P,Peeters F M,Duppen B V 2016Phys.Rev.B93 125425
[20]Niu Z P,Zhang Y M,Dong S H 2015New J.Phys.17 073026
[21]Zhang Y,Sun J,Guo Y 2018J.Phys.D:Appl.Phys.51 045303
[22]Yokoyama T 2013Phys.Rev.B87 241409
[23]Yokoyama T 2014New J.Phys.16 085005
[24]Soodchomshom B 2014J.Appl.Phys.115 023706
[25]Haugen H,Daniel H H,Arne B 2008Phys.Rev.B77 115406

