Hargreaves法在滇中地区的应用及改进

杨 蕊，伍靖伟，王 龙，余 航

(1.云南农业大学水利学院，云南 昆明 650201；2.武汉大学水利水电学院，湖北 武汉 430072)

0 引 言

参考作物需水量(ET0)是确定作物需水量和作物灌溉制度的基础，是灌排工程规划、设计、管理和水资源合理开发利用的基本依据。参考作物需水量的计算方法众多，目前国内外普遍认为联合国粮农组织FAO推荐的Penman-Monteith法(简称P-M法)物理意义明确，计算精度高[1]，但P-M法需要较多的气象资料，在气象资料不齐全时其应用受限。目前主要的简化参考作物需水量计算方法有Hargreaves法(温度法)、 Priestley Taylor法(辐射法)和Irmark-Allen法(经验公式法)等。Hargreaves法(简称H-S法)是联合国粮农组织FAO推荐的气象资料不齐全时计算参考作物需水量的方法，其计算基础为温度，资料来源较为容易、可靠，H-S法在云南地区具有一定的精度和稳定性，但空间变异性较大，使用前需进行修正和改进[2-4]。

近年来，国内学者对H-S法进行修正和改进，提高了其计算精度和适用性。李晨等[5]利用贝叶斯原理对川中丘陵区H-S法的温度指数、温度系数和温度常数进行改进；左德鹏等[6]将渭河流域的H-S法和P-M法计算结果进行回归分析，以修正H-S法的温度常数项；胡庆芳等[7]利用洗牌复合形进化算法对H-S法进行了全局校正；范文波等[8]在玛纳斯河流域对H-S法进行改进；杨永红等[9]在拉萨地区考虑相对湿度对H-S模型进行改进；贾悦等[10]在川中丘陵区考虑辐射的影响对H-S模型进行改进，李丹阳等[11]对H-S法和P-M法的计算结果进行线性拟合从而修正H-S法。

滇中地区包括昆明、曲靖、玉溪、红河、楚雄、大理、丽江7个地(州)市，是云南省国民经济和社会发展的核心区域，简单、精确的参考作物需水量计算方法可为滇中地区的作物灌溉制度制定提供重要基础，对区内水资源综合开发、可持续发展具有重要意义。为提高气象资料不齐时H-S法在滇中地区的精确性，本文引入相对湿度气象要子，应用回归分析及主成分分析对H-S法进行改进，以期提高H-S法在滇中地区的适用性。

1 数据与方法

1.1 数据基础

本文以滇中地区昆明、沾益(曲靖)、玉溪、蒙自(红河)、楚雄、大理、丽江7个气象站56年(1958-2013年)的逐日气象资料作为数据基础，包括平均气温、最高气温、最低气温、平均相对湿度、平均风速、日照时数、平均气压7个逐日气象数据。

1.2 P-M法

P-M法以能量平衡和水汽扩散理论为基础，通过对农田热量的平衡计算求出作物蒸发蒸腾所消耗的热量，把热量换算为水量即为作物需水量。计算公式如下[2]：

式中：ET0为参考作物需水量；Δ为饱和水汽压与温度关系曲线的斜率；Rn为参考作物的冠层净辐射量；G为土壤热通量；γ为干湿表常数；T为平均温度；u2为2 m高处风速；es为饱和水汽压；ea为实际水汽压。

用P-M法计算参考作物需水量最少需要7个气象参数：平均气温、最高气温、最低气温、平均相对湿度、平均风速、日照时数、平均气压。

1.3 H-S法

H-S法是根据蒸渗仪的实验数据得到的基于最高气温、最低气温的参考作物需水量计算方法。计算公式如下[2-4]：

ET0=0.002 3(T+17.8) (Tmax-Tmin)0.5Ra

式中：ET0为参考作物需水量；T为平均温度；Tmax为最高温度；Tmin为最低温度；Ra为大气边缘太阳辐射。

用H-S法计算参考作物需水量只需要3个气象参数：平均气温、最高气温、最低气温。

1.4 主成分分析

为消除气象资料之间存在的复共线性，减少参考作物需水量计算所需的气象资料，简化参考作物需水量计算方法，可利用主成分分析从多元随机的气象资料中提取主成分，在保留原有气象资料大部分信息的同时消除复共线性。

2 H-S法改进

2.1 主成分分析

利用滇中地区7个气象站56年(1958-2013年)的逐日气象资料作为数据，将原始数据进行标准化处理，计算标准化气象数据的相关系数矩阵，求相关系数矩阵的特征值及特征向量。根据计算结果，7个气象站第一主成分的方差贡献率均大于50%，第一主成分包含了原7个气象因子一半以上的信息，因此，取第一主成分替代原7个气象因子的关系。

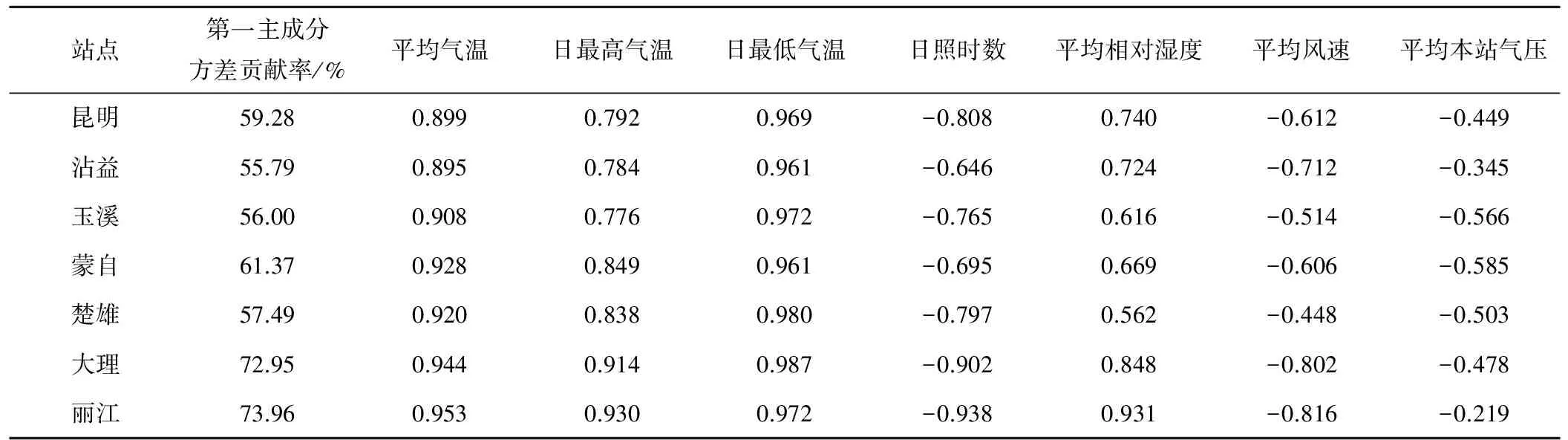
表1 第一主成分方差贡献及特征向量

从第一主成分方差的特征向量(表1)可看出，除沾益外的其他6个站的平均温度、最高温度、最低温度、日照时数、平均相对湿度5个气象因子具有较高的相关性，且包含了大多数信息，沾益平均温度、最高温度、最低温度、平均风速、平均相对湿度5个气象因子具有较高的相关性，且包含了大多数信息。考虑到H-S法计算中的大气边缘太阳辐射参数和日照时数具有相关性，且为了统一引入因子，引入相对湿度气象因子改进H-S法。

2.2 H-S法改进

利用滇中地区7个气象站56年(1958-2013年)的逐日气象资料，分别采用P-M法、H-S法计算昆明的逐日ET0和多年平均逐日ET0，对计算结果进行回归分析。P-M法计算的ET0多记为ET0PM，H-S法计算的ET0值记为ET0HS。以相对湿度RH为自变量，以P-M法和H-S法计算结果的差值ET0PM-ET0HS为因变量进行回归分析，得到回归方程ET0PM-ET0HS=a·RH2+b·RH+c，因此引入相对湿度气象因子后的改进H-S法计算公式为：ET0=0.002 3(T+17.8)(Tmax-Tmin)0.5Ra+a·RH2+b·RH+c。

3 计算结果及对比

3.1 逐日ET0分布

利用滇中地区7个气象站56年(1958-2013年)的逐日气象资料，采用P-M法、H-S法和改进H-S法计算逐日ET0和多年平均逐日ET0，以P-M法计算结果为基础对改进前后H-S法进行对比分析。

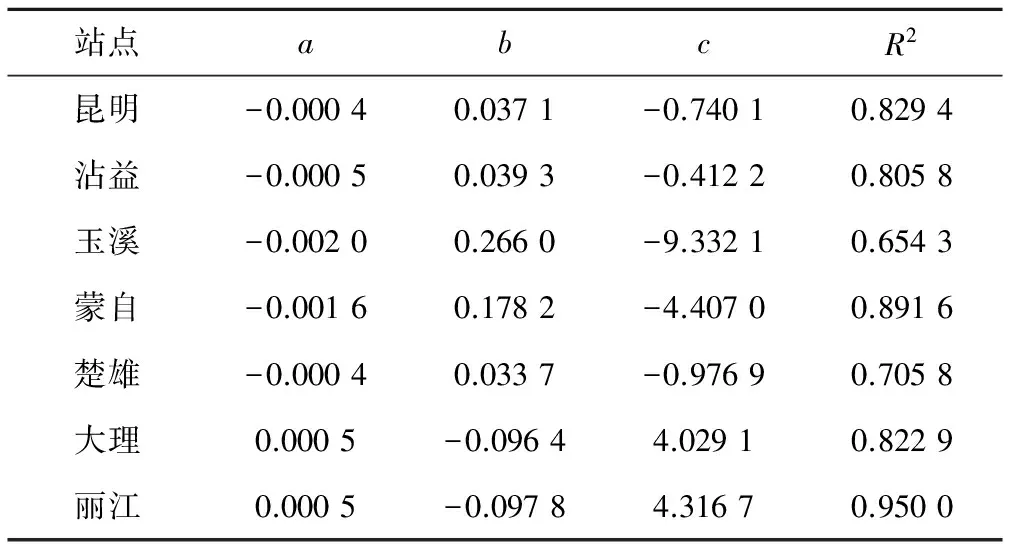
表2 改进H-S法经验参数

改进前后的各站逐日ET0分布曲线见图1。在4-5月之前，昆明、沾益、蒙自、大理和丽江5个站改进前H-S法逐日ET0值比标准值偏小，玉溪和楚雄2个站比标准值偏大，而全部7个站在4-5月后，随着湿度的增大，H-S法普遍呈现出比标准值偏大的结果。随着引入相对湿度气象因子改进H-S法，可有效地改善4-5月后的下半年计算值偏大的缺点。

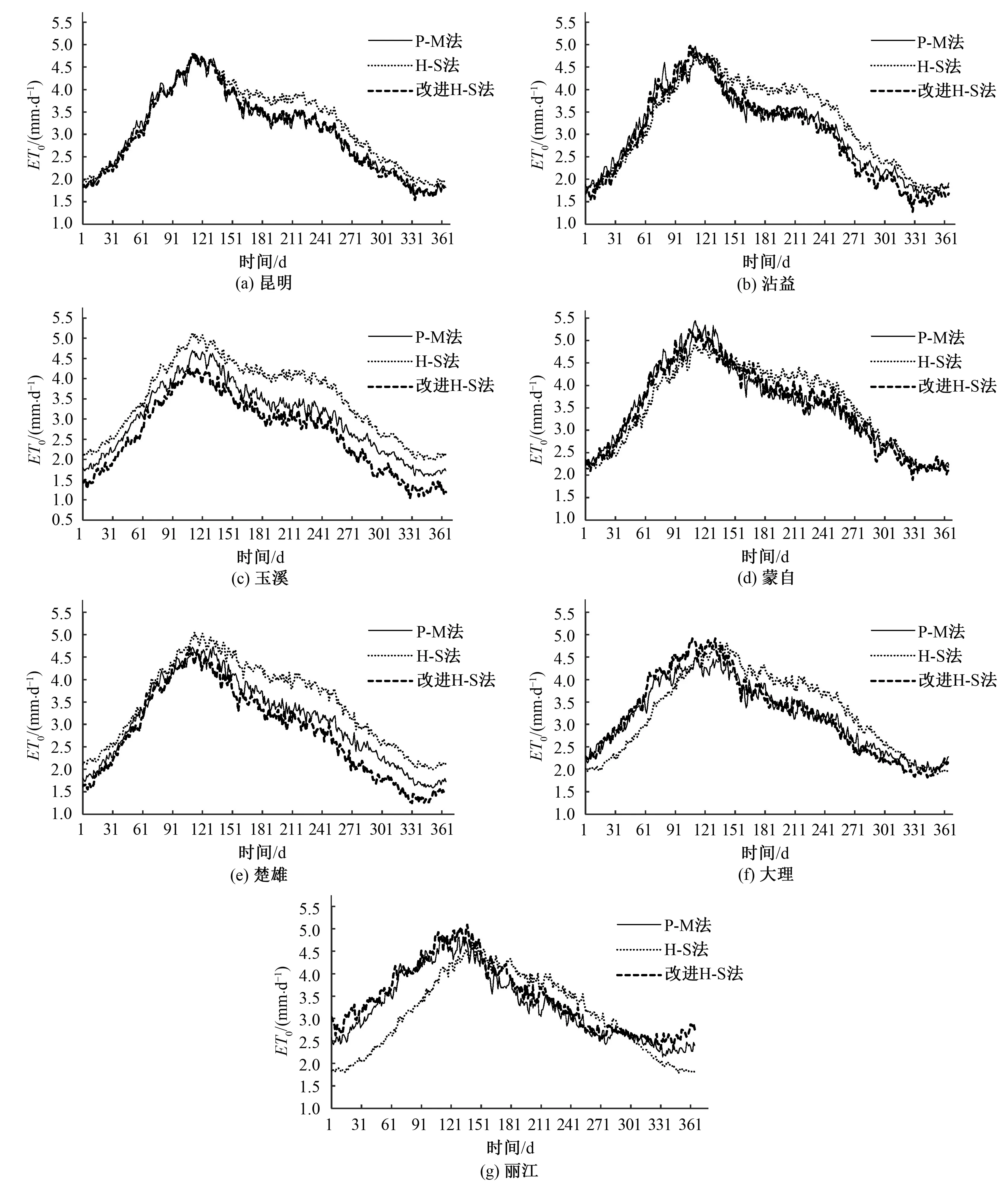
图1 P-M法、改进前后H-S法逐日ET0分布

3.2 逐日ET0偏差

以P-M法计算的多年平均逐日ET0为标准，采用改进H-S法计算多年平均逐日ET0的绝对偏差和相对偏差均得到了不同程度的降低，计算精度得到了不同程度的提高。见表3和图2。

7个站中昆明的精度提高幅度最大，偏差由0.61 mm/d降低到0.27 mm/d，偏差率由20.43%减小到8.91%，改进后偏差率小于5%的天数占全年的90.68%；沾益、玉溪、楚雄、大理、丽江5个站的精度提高幅度相差不大，蒙自的精度提高幅度最小。7个站均可在不同程度上提高4-5月后的计算精度，解决4-5月后计算值偏大的问题；大理和丽江除可解决4-5月计算值偏大的问题，还可解决4-5月前计算值偏小的问题。

3.3 逐日ET0相关性

利用改进H-S法计算多年平均逐日ET0，以P-M法计算的多年平均标准值为基础，得到改进前后H-S法与P-M法计算结果的相关性见表4和图3。改进H-S法的趋势线斜率更接近1，R2均得到提高，改进H-S法和P-M法的逐日ET0计算结果相关性提高，计算结果更为接近。

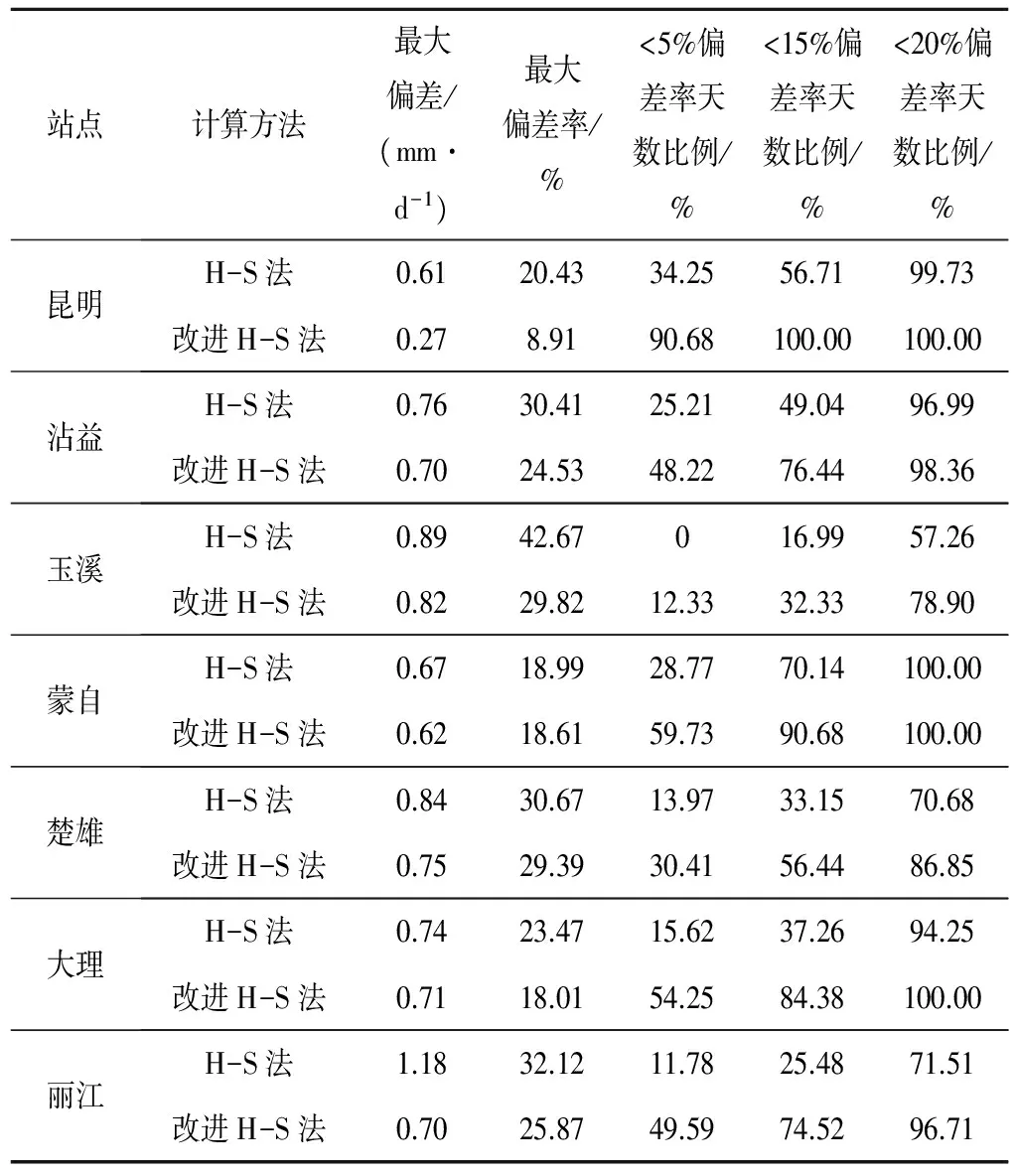
表3 改进前后H-S法计算精度对比

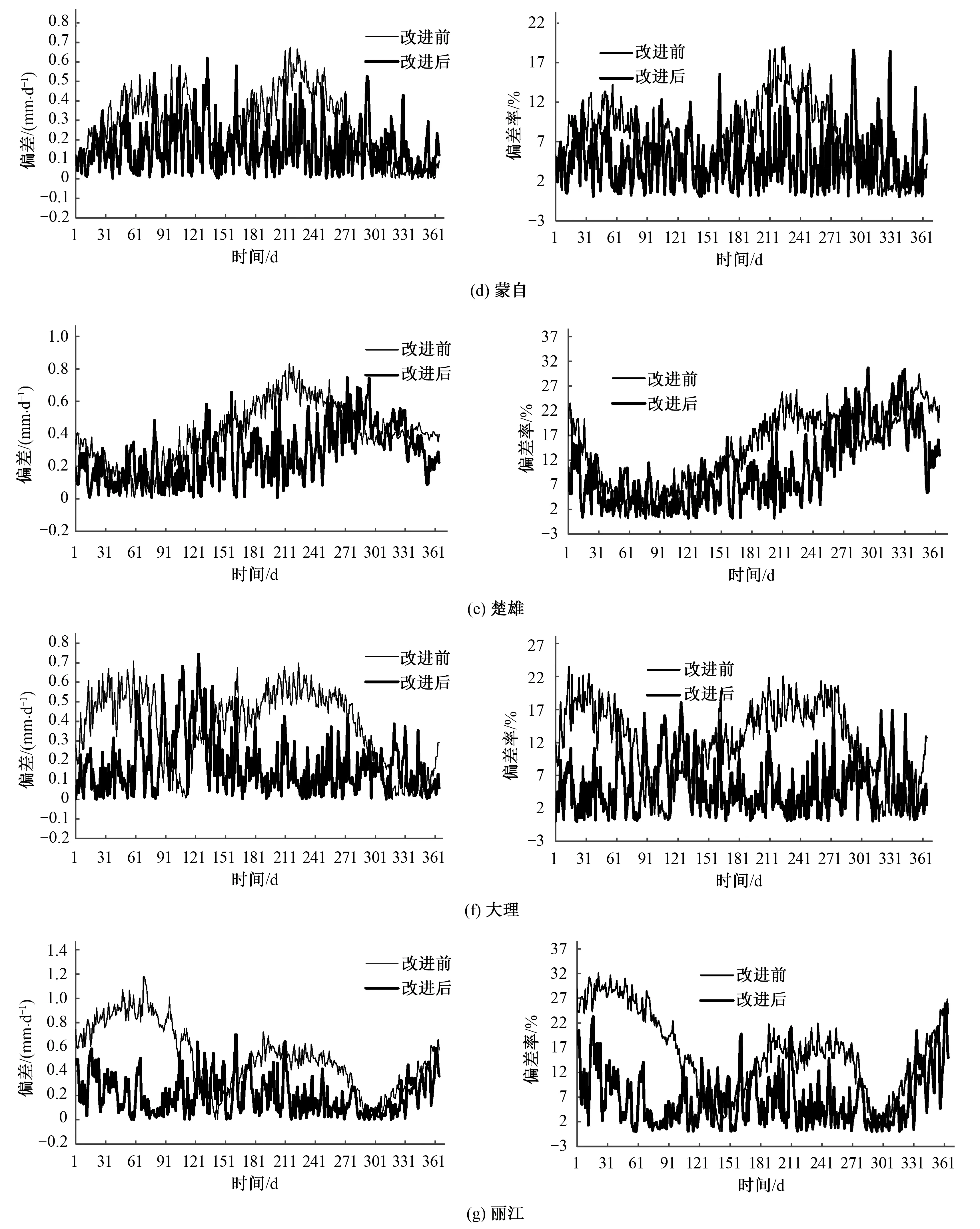
图2 改进前后H-S法偏差和偏差率

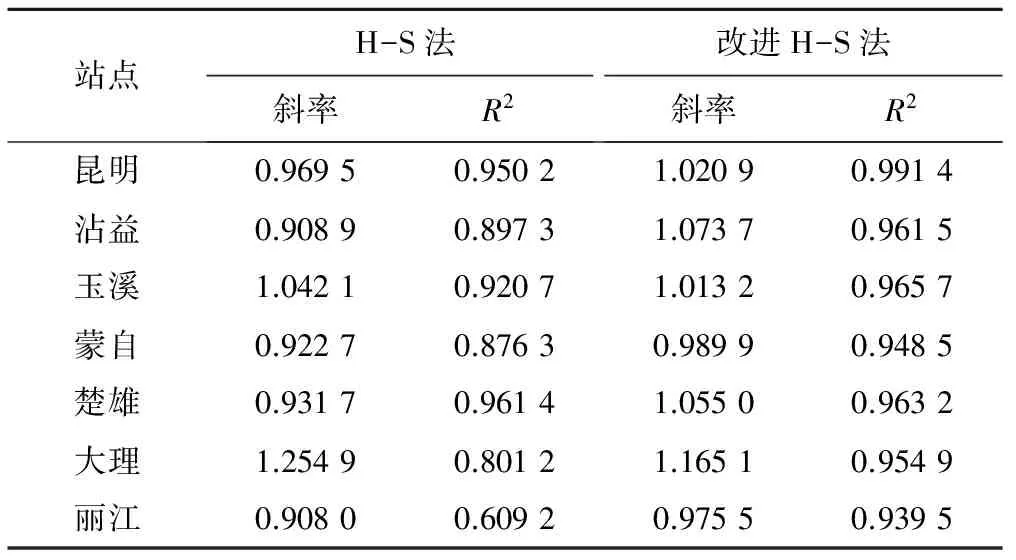
站点H-S法斜率R2改进H-S法斜率R2昆明0．96950．95021．02090．9914沾益0．90890．89731．07370．9615玉溪1．04210．92071．01320．9657蒙自0．92270．87630．98990．9485楚雄0．93170．96141．05500．9632大理1．25490．80121．16510．9549丽江0．90800．60920．97550．9395

3.4 典型年改进结果

以P-M法计算的各站逐年ET0为基础，选取P=75%的年份为典型年，以P-M法计算的逐日ET0为标准，采用改进H-S法计算逐日ET0的误差得到了降低，见表5。由于H-S法适用于计算5 d或更长时间步长的ET0[13]，因此日计算精度提高程度稍低于多年平均逐日ET0精度，但基本可满足滇中地区灌溉制度制定等实际生产设计需要。

4 结果和讨论

在传统回归法的基础上，利用主成分分析法，以滇中地区7个气象站56年(1958-2013年)的逐日气象资料作为数据基础，引入相对湿度气象因子改进H-S法，以P-M法计算的ET0为标准评价改进H-S法的计算精度与适应性。得到如下结论：

(1)改进H-S法和P-M法计算的多年平均逐日ET0值，绝对偏差、相对偏差均得到了降低，改进后H-S法计算精度得到提高。

(2)改进H-S法和P-M法的逐日ET0计算结果相关性提高，计算结果更为相近。

(3)改进H-S法可有效地改善4-5月后计算值偏大的缺点，具有较高的精度。

本文在传统回归法的基础上，利用主成分分析法，引入平均温度气象因子改进H-S法，改进后的H-S法使ET0计算精度得到了提高。改进 H-S法计算结果为日尺度结果，可满足滇中地区ET0研究要求，也可用于该地区灌溉制度的制定等设计需要，可作为滇中地区参考作物需水量ET0的计算方法。

参考文献：

[1] 彭世彰,徐俊增. 参考作物蒸发蒸腾量计算方法的应用比较[J]. 灌溉排水学报,2004,(6):5-9.

[2] 顾世祥,李远华,何大明,等. 参考作物需水量计算方法在纵向岭谷区的应用对比[J]. 灌溉排水学报,2007,(4):21-27.

[3] Hargreaves G H，Allen R G. History and evaluation of Hargreaves evapotranspiration equation [J]. Journal of Irrigation andDrainage Engineering，2003，129(1):53-63.

[4] Allen R G, Pereira L S, Raes D, Smith M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirement[M]. Rome:Food and Agriculture Organization of the United Nations,1998.

[5] 李 晨,崔宁博,魏新平,胡笑涛,龚道枝. 改进Hargreaves模型估算川中丘陵区参考作物蒸散量[J]. 农业工程学报,2015,31(11):129-133,135,134.

[6] 左德鹏,徐宗学,李景玉,等. 气候变化情景下渭河流域潜在蒸散量时空变化特征[J]. 水科学进展,2011,22(4):455-461.

[7] 胡庆芳,杨大文,王银堂,等. Hargreaves公式的全局校正及适用性评价[J]. 水科学进展,2011,22(2):160-167.

[8] 范文波,吴普特,韩志全,等. 玛纳斯河流域ET0影响因子分析及对Hargreaves法的修正[J]. 农业工程学报,2012,28(8):19-24.

[9] 杨永红,张展羽. 改进Hargreaves方法计算拉萨参考作物蒸发蒸腾量[J]. 水科学进展,2009,20(5):614-618.

[10] 贾 悦,崔宁博,魏新平,等. 考虑辐射改进Hargreaves模型计算川中丘陵区参考作物蒸散量[J]. 农业工程学报,2016,32(21):152-160.

[11] 李丹阳,张 涵,王 与,等. 基于Hargreaves的四川地区参考作物蒸发蒸腾量研究[J]. 节水灌溉,2017,(6):85-89.

[12] 魏凤英.现代气候统计诊断与预测技术[M]. 2版. 北京:气象出版社,2007.

[13] Jensen D T，Hargreaves G H，Temesgen B，et al. Computation ofET0under nonideal conditions[J]. Journal of Irrigation and Drainage Engineering，1997，123( 5) : 394-400.