基于SPEI及游程理论的云贵地区1960—2014年干旱时空变化特征

芦佳玉，延军平*，李英杰

(1.陕西师范大学 地理科学与旅游学院， 陕西 西安 710062； 2. 地理学国家级实验教学示范中心(陕西师范大学)， 陕西 西安 710062)

0 引 言

随着全球气温的不断升高，陆地存在不同程度的干旱化趋势，其中欧亚大陆、非洲大陆干旱化趋势最为严重[1]. 近年来，我国干旱事件发生频率有所上升，且持续时间长、影响范围广、造成危害大. 现有研究中，针对云贵地区干旱的研究较少，大多学者都将研究区放大至整个西南地区[2-4]，或缩小至以省为单位[5]. 而云贵两省大部分地处云贵高原，因此，将云贵两省相结合进行研究十分必要. 云贵地区同时受南亚季风和东亚季风的影响，对气候变化较为敏感，且云贵地区是全球典型的低纬高原区之一，地理区位特殊[6]， 其在全球变暖的气候背景下，气象灾害更为突出. 如2005年春季云南异常干旱、2009—2010年西南遭受罕见的三季连旱、2009年秋后云南遭受了持续4 a的干旱[7-8]. 因此研究云贵地区长时间序列的干旱变化规律，可对云贵地区干旱灾害进行预警，对云贵地区粮食安全、生态建设及经济发展有重要意义.

大多数学者主要从干旱历时及干旱强度两方面对干旱事件进行分析[9-13]，而对于防旱抗旱来说，需要关注的是干旱发生的频率，只有了解干旱发生的频率及其周期性才能有效防备干旱的发生. 因此，对于干旱频率的分析是目前急需解决的问题[14].现有的频率分析中，常常使用Copula函数来构造多维变量间的联合分布[15-16]. 这种分布虽在一定程度上取得了进展，但受主观干扰的影响较大[17].而游程概率理论则不必假定变量所服从的分布概率，无论独立与否均能从简单的统计游程现象入手，揭示游程现象发生的概率[18]. 马秀峰等[19]将游程理论运用到水文干旱中，提出了可用于干旱研究的游程重现期公式. 标准化降水蒸散发指数(SPEI)是VICENTE-SERRANO等[20]在标准化降水指数(SPI)的基础上通过引入潜在蒸散量构建的，融合了SPI和帕尔默干旱指数(PDSI)的优点，SPEI用水分亏缺量和持续时间2个因素来描述干旱，可以很好地表示干旱的程度. 所以本文运用SPEI指数结合游程理论及经验正交函数(EOF)等，对云贵地区近55 a不同干旱历时及不同干旱强度的干旱重现期的变化规律及特征进行研究.

1 研究资料与方法

1.1 研究区概况

云贵地区包含云南省及贵州省，总面积达57.02×104km2. 该区主体为云贵高原，受南亚季风影响，干湿季分明，属典型的低纬高原气候.年平均降水量分别为749～1 068 mm和682～1 134 mm，年均气温分别为15～17 ℃和14～16 ℃，云贵地区气候一致性较高. 由于受季风及地势的影响，该地区6～8月降水量可达全年降水量的60%[20]，其他3季降水量较少，蒸发量较多；且降水量空间分布也不均匀，大致呈现沿纬度带由南向北逐渐减少的趋势, 导致干旱事件频发，尤其是秋、冬、春3季连旱，对当地的生产生活造成极大影响.

1.2 资料来源

气象资料来源于中国气象科学数据共享服务平台(http： //data.cma.cn/site/index.html ). 选取1960—2014年中国地面气候资料月值数据集，为保证数据的完整性和连续性，采用监测数据较为完整的49个台站的气象数据(贵州省19个，云南省30个). 数据基本完整，对个别台站的缺失数据采用SPSS21.0最大期望算法(EM估计)进行插补，经处理后的数据具有良好的连续性和代表性(见图1).

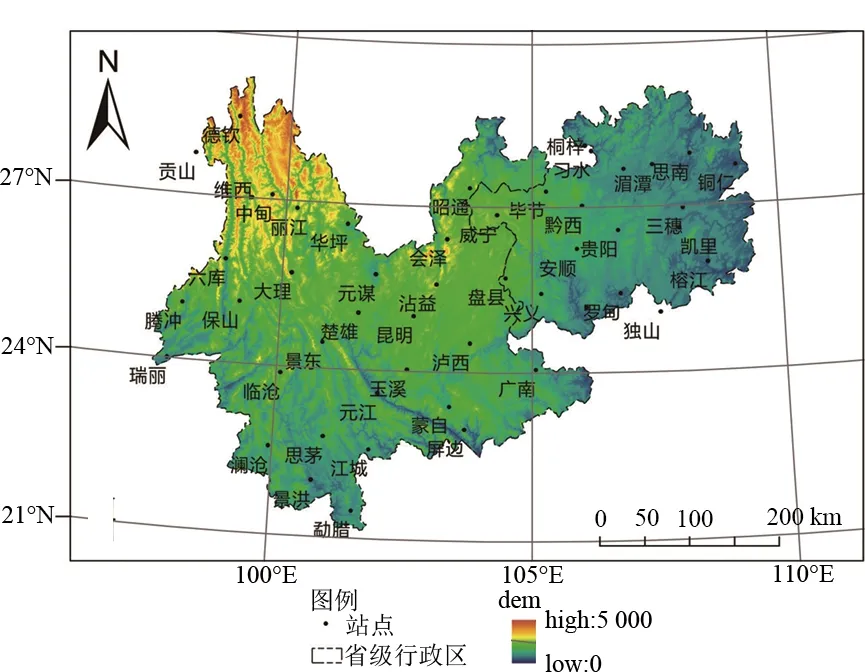
图1 云贵地区49个气象站点空间分布Fig.1 Spatial distribution of 49 meteorological stations in Yun-Gui area

1.3 研究方法

1.3.1标准化降水蒸散发指数

标准化降水蒸散发指数(SPEI)是在标准化降水指数(SPI)的基础上发展而来的，该指数不仅考虑了温度及降水的影响，还综合考虑了蒸散作用，继承了PDSI对蒸散量的敏感性和SPI的长序列尺度及计算的简便性，是较为理想的干旱指标[21]. 同时与SPI一样，SPEI可以计算多尺度即月尺度(SPEI1)、季节尺度(SPEI3)、半年尺度(SPEI6)、年尺度(SPEI12)的SPEI值. 计算方法如下：

首先计算水汽平衡：

Di=Pi-PETi,

(1)

其中，Pi为降水，PETi为潜在蒸发量，可通过Thornthwaite方法[21]求得.

然后采用3参数的log-logistic概率分布函数对Di数据序列进行正态化，计算每个数值对应的SPEI指数：

(2)

(3)

参数α，β，γ 的计算公式如下：

(4)

(5)

γ=ω0-αΓ(1+1/β)Γ(1-1/β)，

(6)

其中，ω0，ω1，ω2为数据序列Di的概率加权矩,

(7)

(8)

其中，N为参加计算的月份数.

接着对累积概率进行标准化，当P≤0.5时，P=F(x)；当P>0.5时，P=1-F(x)，且SPEI的符号逆转：

(9)

(10)

其中,常数C0=2.515 517，C1=0.802 853，C2=0.010 328，d1=1.432 788，d2=0.189 269，d3=0.001 308. 干旱分类标准见表1[21].

表1 SPEI值干旱等级分类标准

1.3.2 游程理论

运用游程理论对干旱事件进行识别，给定一个截取水平k(k=SPEI对应的干旱等级),截取随时间变化的离散系列Xt(t=1,2,…,n).当随机变量在一个或多个时间内连续大于截取水平时，出现正游程，反之则出现负游程[18]. 在干旱研究中，负游程的长度称为干旱历时，干旱强度为干旱历时与截取水平包含的面积. 根据游程理论计算游程长度的重现期，计算步骤如下：

首先计算某个游程长度(干旱历时)发生的平均概率P：

(1)

其中，x为指定截取水平下的干旱历时；n为多年逐月降水系列月数；g(x)为干旱历时为x的发生次数.

接着计算该状态游程的期望长度E：

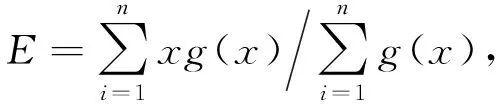
(2)

式中，g(x)为期望次数，计算公式为

(3)

将式(3)代入式(2), 可得：

E=n/[1+(n-1)(1-P)].

(4)

然后，为了消除非独立作用的影响，由式(4)反推出游程长度的迁移概率Pz：

Pz=n(E-1)/[E(n-1)].

(5)

根据式(5)得到涵盖历时与强度在内的一维带参数的游程概率分布函数：

(6)

游程长度重现期[18]定义为： 若连续进行T(x)次随机试验，其中出现一次游程长度不小于x的事件，就称为T(x)游程长度不小于x的重现期，

T(x)=x+(Pz-x-1)/(1-Pz).

(7)

T(x)通常用年来分析重现期.本文选取月尺度降水系列分析重现期，即将T(x)转换为T′(x)：

T′(x)=T(x)/12.

(8)

1.3.3 经验正交(EOF)

经验正交函数(简称EOF)是针对气象要素进行的，其基本原理是把包含Q个空间点(变量)的场随时间变化进行分解.

将各气象台站观测资料作距平处理或标准化距平处理，可得描述该区域气象要素场的资料矩阵Xm×n. 设有m个台站，每个台站有n个样本值，每个样本值表示为xji，i=1,2,…,m，j=1,2,…,n，xj为第j个台站：

经验正交函数分解是将X分解为空间函数V和时间函数Z：

X=VZ，

其中，

分解步骤如下：

(2) 求∑的特征值和特征向量.

(3) 特征值为λ1≥λ2≥…≥λm，对应的特征向量为v1≥v2≥…≥vn，并组成矩阵V=(v1,v2,…vm)，V是空间上的函数，每一列表示一个空间典型场，且只与空间有关.

(4) 根据Z=VTX求Z，Z是时间上的函数，其

值由典型空间场V和实际空间场X唯一确定. 将时间函数Z看作典型场的权重系数，不同时间的要素场是若干个典型场按不同权重线性叠加的结果.

(5)X=VTZ即为最终的展开结果.

2 结果分析

2.1 干旱指数年及四季变化特征

通过分析云贵地区近55 a干旱指数的年及四季变化特征(见图2)可知，云贵地区年(图2(a))和四季SPEI指数均呈下降趋势，干旱化趋势明显，且下降趋势年(-0.14 a-1)>秋季(-0.012 a-1)>冬季(-0.01 a-1)>夏季(-0.009 a-1)>春季(-0.004 a-1). 除春季外，其他季节的变化趋势倾向率均通过90%的显著性水平检验.

图2 云贵地区年及四季SPEI值及趋势图Fig.2 SPEI values of the four seasons and trend in Yun-Gui area

从图2(a)的滑动平均曲线可以看出，20世纪60—70年代，SPEI的年变化与季节变化(除春季外)都呈小幅波动或逐渐上升趋势，而60年代春季(见图2(b))发生了2次较为严重的干旱事件，分别为1963和1967年，其SPEI所显示的等级也均在严重干旱及中等干旱之间. 70—80年代，SPEI年及季节变化都有小幅上升，且在此期间均无严重干旱事件发生，说明此时期云贵地区呈变湿趋势，1979年虽发生了春旱，但不影响整体的变化趋势. 80—90年代，除秋季(见图2(d))SPEI值基本无变化外，其他3季及年SPEI均呈下降趋势，且在1987年出现春旱现象. 90年代至21世纪初，春季、夏季(见图2(d)、(c))及年SPEI值均呈上升趋势，而秋季和冬季(见图2(d)、(e))SPEI值分别呈缓慢下降和小幅波动趋势，没有出现极端干旱事件. 21世纪初至今，四季及年SPEI值均呈下降趋势，且年尺度SPEI值下降趋势最为明显，2009年及2011年发生了严重干旱现象. 综上所述，20世纪80年代前及21世纪后，年变化与季节变化一致性较强，而20世纪80年代至21世纪初，年变化与季节变化一致性较弱.

2.2 干旱强度变化特征

本文选取各站点中等以上干旱事件之和建立云贵地区55 a来年干旱强度指标[26]，SPEI<-1，即中等干旱以上的事件与干旱历时d围城的面积之和称干旱强度s，详见图3，数值越高说明干旱强度越大.

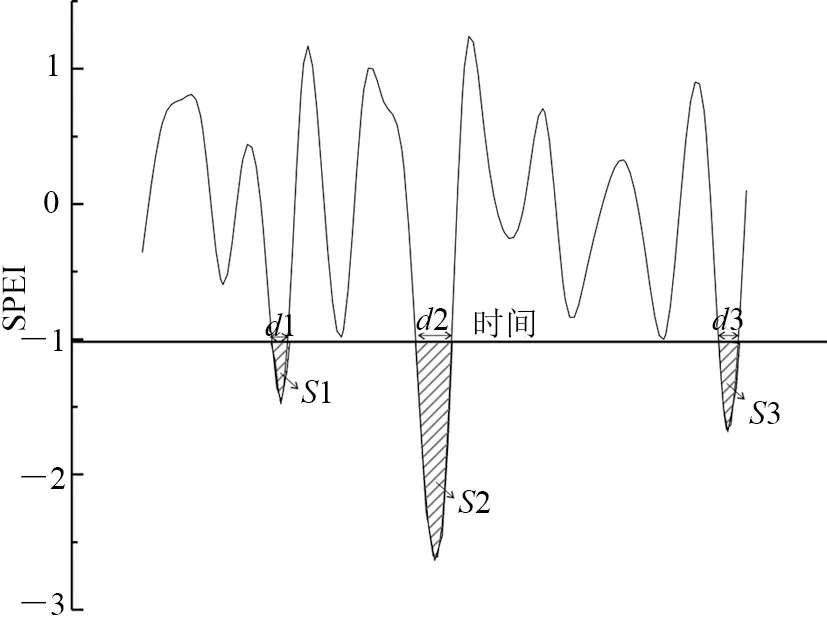
图3 干旱强度识别过程Fig.3 Identification process of the drought intensity

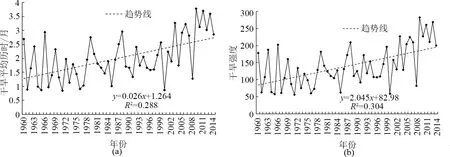
图4 云贵地区1960—2014年干旱强度及干旱历时变化Fig.4 Annual drought intensity and temporal sequence of drought in Yun-Gui area during 1960 to 2014

1960—2014年云贵地区年干旱强度及干旱历时变化如图4所示. 干旱历时与干旱强度在一定程度上可以反映干旱的强弱.从图4可以看出，干旱历时与干旱强度变化趋势基本一致，云贵地区近55 a来干旱化趋势明显，发生严重干旱的年份历时较长，干旱强度相应也较大. 干旱强度以2.045 a-1的速率增强，最强值出现在2009年，之后在最强值附近波动，这与云贵地区实际发生严重干旱的年份相符，说明SPEI在云贵地区能很好地反映实际干旱情况，有较强的适应性.

2.3 干旱重现期

干旱重现期是指某次干旱强度(历时)大于给定强度(历时)值的时间间隔. 间隔越长，干旱发生的频率越小；间隔越短，发生的频率越大. 运用游程理论及SPEI干旱等级分布给定截取水平k，令k=-0.5(轻旱及以上)，-1(中等干旱及以上)，-1.5(严重干旱及以上)分别对云贵地区49个站点干旱历时的迁移概率进行统计.

勐腊站所在气候分区为北热带，贵阳站所在气候分区为中亚热带，故选取勐腊站及贵阳站作为代表站. 以勐腊站(图5(a))及贵阳站(图5(b))为例，选取不同干旱等级下的干旱历时，利用其与理论概率分布的关系，得到不同气候分区站点的干旱历时与理论概率分布的趋势大致相同，随着干旱历时的增加，理论概率密度均呈指数递减；在同一干旱等级下，当干旱历时达到或超过最大统计长度时，理论概率密度就会无限接近于0. 同一干旱历时在不同干旱等级下，当干旱等级越高时其曲线越靠下，也就是说，在干旱历时相同的情况下，干旱等级越高，其理论概率分布越小.

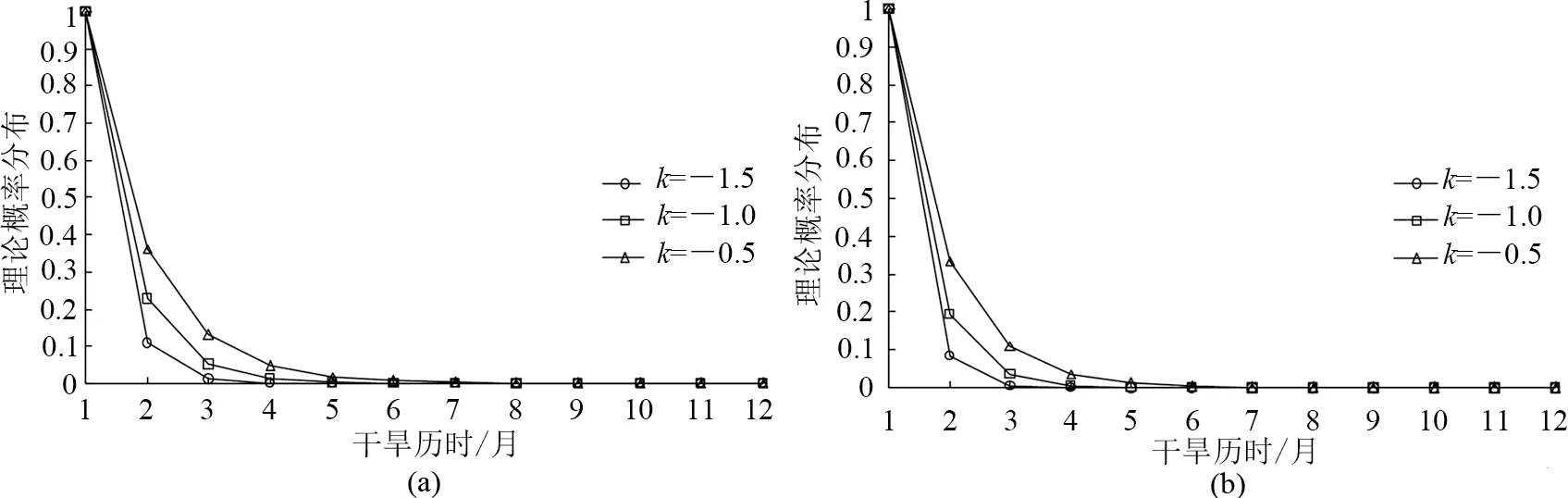
(a) 勐腊 Mengla (b) 贵阳Guiyang图5 勐腊站及贵阳站干旱历时与理论概率分布Fig.5 Drought duration and theoretical probability distribution of Mengla and Guiyang station

干旱等级越小对人类影响越小，持续时间为2～5个月的干旱对人类生产生活的影响较大，持续时间大于5个月的干旱对人类的影响巨大，但出现的概率较小[18]. 所以选取k= -1(中等及以上干旱等级)，绘制2～5个月各站点干旱重现期的空间分布图(见图6). 由图6可知，云南省干旱重现期小于贵州省，且27°N以北地区干旱重现期较长.

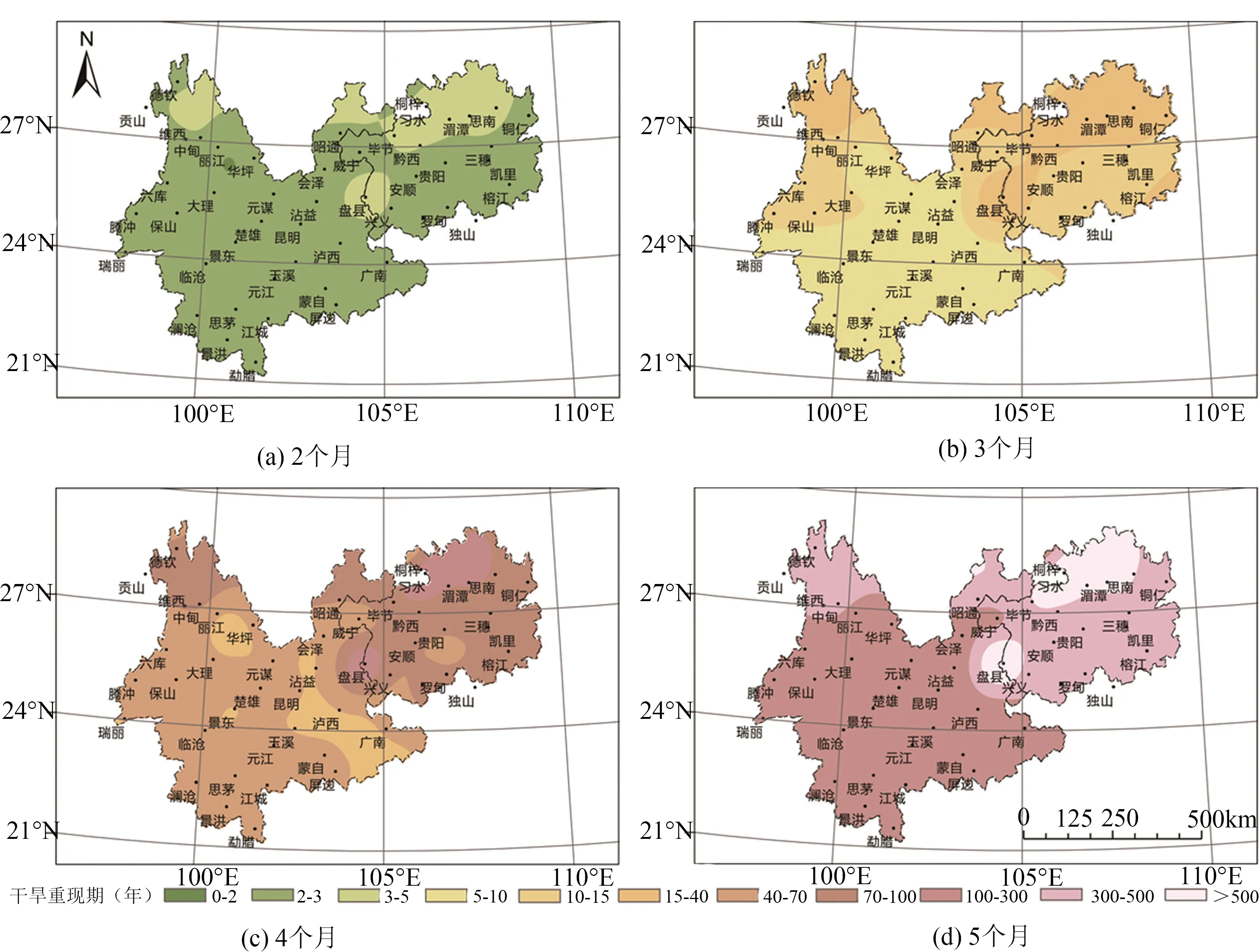
图6 云贵地区干旱历时2～5个月的重现期分布图Fig.6 Return period distribution of drought duration which in 2-5 months in Yun-Gui area

由图6(a)可知，云贵地区干旱历时为2个月的干旱重现期整体呈现“全区一致，南北略有差异”的分布特征. 大部分为2～3 a，在云贵地区的北部及云贵地区交界处盘县一带重现期为3～5 a. 分析图6(b)可知，云贵地区干旱历时为3个月的重现期的空间分布大致可以分为三部分，第一部分为云南省南方大部，重现期为5～10 a；第2部分为贵州省南部及云南省中西部，重现期为10～15 a；第3部分为贵州省北部及云贵地区交界处及云南省德钦一带，重现期为15～40 a. 由图6(c)可知，干旱历时为4个月的重现期分布较为分散，但大致以云贵两省为分界线. 云南省大部分地区重现期为40～70 a，其中玉溪、昆明、沾益、泸西一带及大理、景东重现期为15～40 a；贵州省大部分地区及云南省中甸德钦一带重现期为70～100 a，在云贵交界处的盘县一带及北部的习水、遵义一带，重现期可达100～300 a. 由图6(d)可知，历时为5个月的严重干旱重现期呈现以省界为分界线，云南地区的干旱重现期均小于贵州地区，云南省大部分干旱重现期在100～300 a，而贵州省大部分干旱重现期在300～500 a.

综合上述分析，云贵地区干旱历时不同，干旱重现期分布也不相同，且干旱历时越长，干旱重现期越长. 而干旱历时也可以反映一个地区的干旱严重程度，即在同等干旱等级情况下，历时越长，干旱程度越严重. 干旱重现期表示的是干旱发生的频率，在同等干旱等级和同等历时长度的情况下，重现期越短说明干旱发生的次数越多，越容易受干旱的影响. 从图6所示的所有干旱重现期的空间分布来看，云南省比贵州省更易受到干旱的影响，这与实际情况较为吻合. 其原因在于降水集中程度不同[22]，云南省有明显的雨季，其6—8月的降水量占全年降水总量的60%. 贵州省的降水量则没有如此集中，所以，云南省比贵州省更易干旱，且易发生春旱及秋旱. 从纬度上看，贵州省的纬度高于云南省，低纬度地区蒸散量大于高纬度地区，同时降水量也呈现贵州省大于云南省的分布状态[23]. 再次出现干旱时间间隔最长处位于云贵交界一带，因交界处由乌蒙山阻隔，主峰位于盘县一带，地势高、蒸散量少，且印度洋及大西洋的水汽输送都会聚集于此，使其降水量增加，故此处较少发生干旱.

2.4 干旱空间分布特征(EOF分解展开)

为进一步分析云贵地区近55 a的干旱空间分布特征，对该地区SPEI 12进行EOF分解，前5个特征值累计贡献率达到60.04%(见表2)，其中前2个特征值的贡献率较大，分别为30.83%和12.35%，特征较为明显，基本可以反映云贵地区干旱的时空分布特征，而剩余的特征值贡献率较小，特征不明显.

将前2个特征值对应的特征向量运用样条插值法进行空间分析(见图7和图8). 由第1空间模块可知，云贵地区第一特征向量值均为正值，表明云贵地区干旱变化在空间分布上有良好的一致性. 但这种变化在不同区域表现的强烈程度不同，云南省东部及保山大理一带第一特征向量数值较大，是第一模态的主要控制中心. 而在云贵交界处的盘县一带，形成低值中心，第一模块对此地区的控制较弱，由此向外控制能力逐渐增强. 从第一模块对应的时间系数中可以看出，20世纪60年代到21世纪初，干旱与洪涝交替变化，21世纪后，时间系数大多在负值区波动，说明该区域在此时段普遍处于干旱状态. 这与韦小雪等[24]的东亚夏季风强度明显减弱的时间点一致，说明东亚季风偏弱时，云贵地区降水量偏少，干旱事件较多. 由此看来，第一空间模块实际上反映的是云贵地区全区的干旱平均状态.

表2 云贵地区SPEI 12的EOF特征值

第二特征贡献率只占12.35%，可作为分析云贵干旱空间分布的参考. EOF展开的第二空间模块与第一空间模块有明显不同，由第二模块的空间分布可知，云南省中部大部分区域为正值中心，逐渐向两边扩散，基本呈经向分布，揭示了两省干旱呈反相位变化. 结合第二模块时间系数，20世纪60年代，云南与贵州交替进入湿润期或干旱期；70年代，时间系数几乎为负值，表明这段时间云南省处于湿润期，而贵州省处于干旱期；20世纪80年代至21世纪初，时间系数在正负之间波动，表明云南省与贵州省交替进入干旱期；21世纪初至2010年，时间系数几乎为正，与70年代特征相反，说明云南省在湿润期后经历了一段时间震荡后转为干旱期，而贵州省在经历了一段时间干旱期震荡后转为湿润期. 云贵地区第二模态的干湿转变与东亚及南亚夏季风边界变化有关[25].20世纪60年代前，边界处于偏东年，云南省受南亚季风影响，降水较多，干旱现象不明显；70—90年代，季风边界处于东西振荡状态，所以云贵地区处于干湿振荡转变时期；90年代后，边界偏西，云南几乎接收不到由南亚夏季风带来的水汽，同时，由于山脉的阻隔，东亚季风对云南的控制较弱，水汽输送不足，导致云南地区干旱现象严重.

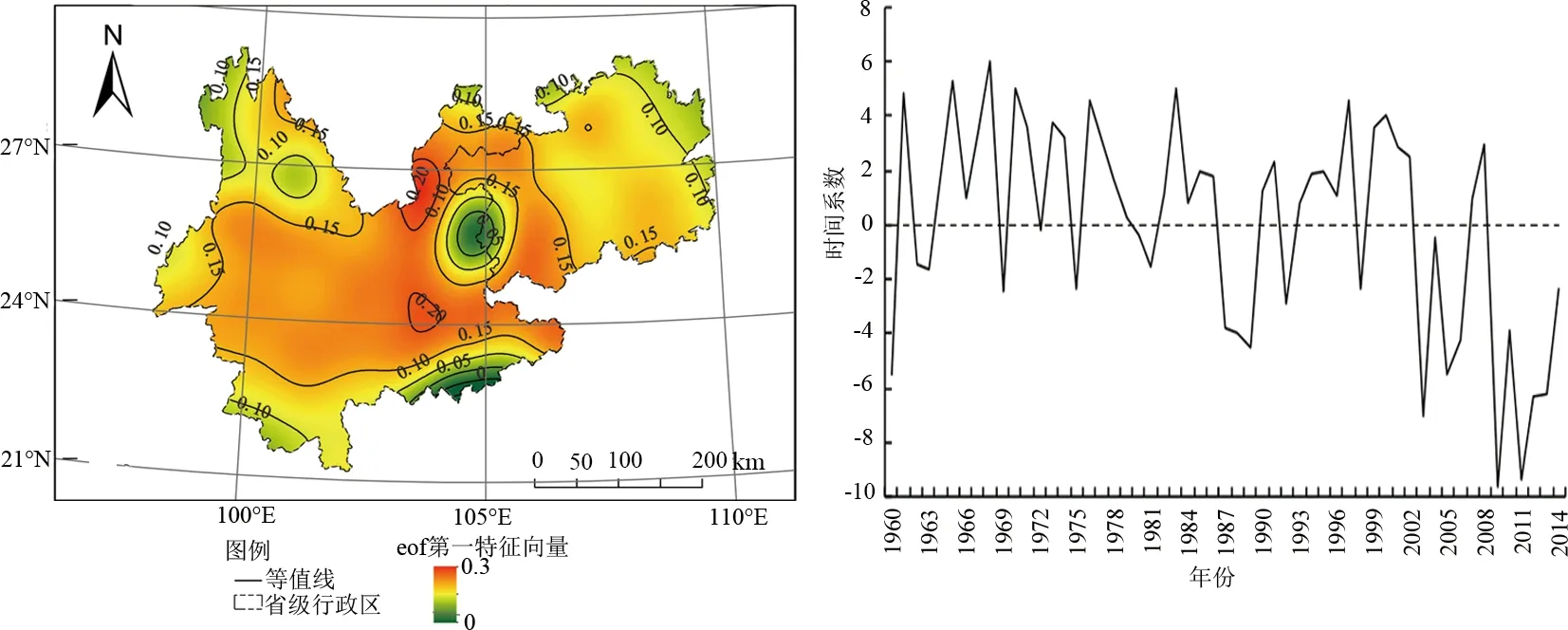
图7 云贵地区EOF展开第一空间模态及时间系数Fig.7 The first spatial mode of EOF and temporal coefficients in Yun-Gui area

图8 云贵地区EOF展开第二空间模态及时间系数Fig.8 The second spatial mode of EOF and temporal coefficients in Yun-Gui area

3 结论与讨论

运用标准化降雨蒸散量指数(SPEI)、游程理论及经验函数正交法对云贵地区干旱化的时空特征进行了分析，得到以下结论：

3.11960—2014年云贵地区以21世纪初为界限，无论是年尺度或季尺度都存在由湿转干的趋势. 年尺度干旱趋势明显大于季尺度；四季中，秋季的干旱趋势最为明显，虽然春、冬季干旱趋势并不明显，但发生重大干旱的次数较多. 未来春旱和秋旱仍是关注的重点，而冬季旱灾也应有所重视.

3.2近55 a来云贵地区不仅干旱趋势明显，强度也在逐渐增强，且在2009年达到最强值. 而2009年也是云贵地区发生严重干旱时期，干旱持续时间和干旱严重程度都较大，这与干旱强度监测结果一致，说明SPEI在监测云贵地区干旱中有较好的指示作用.

3.3云贵地区在同一干旱历时、不同干旱等级下发生干旱事件的概率不同，干旱等级越小时，发生的概率越大，反之亦然. 在同一干旱等级、不同干旱历时，干旱事件发生的概率不同，历时越长发生的概率越小.

3.4一定干旱等级下，历时越长，干旱重现期越长. 在空间分布上，云南省干旱重现期小于贵州省，且在27°N以北地区重现期较长，即云南省干旱事件多于贵州省，27°N以北地区干旱事件发生次数较少.

3.5EOF展开的第一模块反映的是云贵地区受季风系统控制，干旱变化一致性较好. EOF展开的第二模块反映了由于地形差异及受乌蒙山的阻隔，云南省与贵州省干旱变化基本呈反相位. 即整体呈一致性，局部存在微弱差别.

基于SPEI对近55 a云贵地区干旱指数变化趋势、干旱强度、干旱重现期及SPEI的EOF空间展开模块进行了分析研究， 揭示云贵地区干旱化趋势明显，且均在21世纪初出现由湿转干的迹象. 分析发现，云贵地区干旱化是在我国气候变化的大背景下产生的，其干旱特征与全国大部分地方的趋势相似. 研究发现，季风边缘的变化对云贵地区干旱有影响，在今后的研究中应更加关注云贵地区干旱的成因和机制，比如与季风环流的关系，以及与ENSO事件之间的联系，从而从根本上对干旱进行控制，降低干旱给云贵地区的经济和生产造成的损失.

参考文献(References)：

[1] 张勃, 张耀宗, 任培贵,等. 基于SPEI法的陇东地区近50 a干旱化时空特征分析[J].地理科学, 2015, 35(8)： 999-1006.

ZHANG B, ZHANG Y Z, REN P G, et al. Analysis of drought spatial-temporal characteristics based on SPEI in Eastern Region of Gansu in recent 50 years [J].ScientiaGeographicaSinica, 2015, 35(8)： 999-1006.

[2] 李奇临, 范广洲, 周定文,等. 综合气象干旱指数在2009～2010年西南干旱的应用[J].成都信息工程学院学报, 2012, 27(3)： 267-272.

LI Q L, FAN G Z, ZHOU D W，et al. Application of meteorological drought composite index in Southwest China in 2009—2010[J].JournalofChengduUniversityofInformationTechnology, 2012, 27(3)： 267-272.

[3] 王东, 张勃, 安美玲,等. 基于SPEI的西南地区近53 a干旱时空特征分析[J].自然资源学报, 2014(6)： 1003-1016.

WANG D, ZHANG B, AN M L. Temporal and spatial distributions of drought in Southwest China over the past 53 years based on standardized precipitation evapotranspiration index[J].JournalofNaturalResources, 2014(6)： 1003-1016.

[4] 杨金虎, 张强, 王劲松,等. 近60 a来西南地区旱涝变化及极端和持续性特征认识[J].地理科学, 2015, 35(10)： 1333-1340.

YANG J H, ZHANG Q, WANG J S, et al. Extreme and persistent feature of drought and flood of Southwest China in past 60 years[J].ScientiaGeographicaSinica,2015, 35(10)： 1333-1340.

[5] 杨晓静, 左德鹏, 徐宗学. 基于标准化降水指数的云南省近55年旱涝演变特征[J].资源科学, 2014, 36(3)： 473-480.

YANG X J, ZUO D P, XU Z X. Characteristics of droughts and floods analyzed using the standardized precipitation index in Yunnan province during the past 55 years[J].ResourcesScience, 2014, 36(3)： 473-480.

[6] 方兰.云贵地区旱涝变化时空结构及趋势判断[D]. 西安： 陕西师范大学, 2013.

FANG L.Yunnan-GuizhouRegionChangesinTimeandSpaceStructureandtheTrendofFloodandJudgment[D]. Xi’an： Shaanxi Normal University,2013.

[7] 熊光洁, 张博凯, 李崇银,等. 基于SPEI的中国西南地区1961—2012年干旱变化特征分析[J].气候变化研究进展, 2013, 9(3)： 192-198.

XIONG G J, ZHANG B K, LI C Y, et al. Characteristics of drought variations in Southwest China in 1961-2012 based on SPEI [J].AdvancesinChimateChangeResearch, 2013, 9(3)： 192-198.

[8] 民政部国家减灾中心. 全国自然灾害基本情况分析(2013年上半年)[J].中国减灾, 2013(8)： 61-62.

NDRCC. The national natural disasters basic situation analysis (In the first half of 2013)[J].DisasterReductioninChina, 2013(8)： 61-62.

[9] 陈少勇, 郭俊瑞, 吴超. 基于降水量距平百分率的中国西南和华南地区的冬旱特征[J].自然灾害学报, 2015(1)： 23-31.

CHEN S Y, GUO J R, WU C. Characteristics of winter drought in Southwest-South China based on precipitation anomaly percentage[J].JournalofNaturalDisasters, 2015(1)： 23-31.

[10] 王明田, 王翔, 黄晚华,等. 基于相对湿润度指数的西南地区季节性干旱时空分布特征[J].农业工程学报, 2012, 28(19)： 85-92.

WANG M T, WANG X, HUANG W H, et al. Temporal and spatial distribution of seasonal drought in Southwest of China based on relative moisture index[J].TransactionsoftheChineseSocietyofAgriculturalEngineering, 2012, 28(19)： 85-92.

[11] 赵海燕, 高歌, 张培群,等. 综合气象干旱指数修正及在西南地区的适用性[J].应用气象学报, 2011(6)： 698-705.

ZHAO H Y, GAO G, ZHANG P Q, et al. The modification of meteorological drought composite index and its application in Southwest China[J].JournalofAppliedMeteorologicalScience, 2011(6)： 698-705.

[12] 袁云, 李栋梁, 安迪. 基于标准化降水指数的中国冬季干旱分区及气候特征[J].中国沙漠, 2010, 30(4)： 917-925.

YUAN Y, LI D L, AN D. Winter aridity division in China based on standardized precipitation index and circulation characteristics[J].JournalofDesertResearch, 2010, 30(4)： 917-925.

[13] 苏宏新, 李广起. 基于SPEI的北京低频干旱与气候指数关系[J].生态学报, 2012, 32(17)： 5467-5475.

SU H X, LI G Q. Low-frequency drought variability based on SPEI in association with climate indices in Beijing[J].ActaEcologicaSinica, 2012, 32(17)： 5467-5475.

[14] 程亮, 金菊良, 郦建强,等. 干旱频率分析研究进展[J].水科学进展, 2013, 24(2)： 296-302.

CHENG L, JIN J L, LI J Q, et al. Advance in the study of drought frequency analysis[J].AdvancesinWaterScience, 2013, 24(2)： 296-302.

[15] 李计, 李毅, 贺缠生. 基于Copula函数的黑河流域干旱频率分析[J].西北农林科技大学学报(自然科学版), 2013(1)： 213-220.

LI J, LI Y, HE C S. Frequency analysis of drought in Heihe river basin using Copula function[J].JournalofNorthwestA&FUniversity(NaturalScienceEdition), 2013(1)： 213-220.

[16] 张强, 李剑锋, 陈晓宏,等. 基于Copula函数的新疆极端降水概率时空变化特征[J].地理学报, 2011, 66(1)： 3-12.

ZHANG Q, LI J F, CHEN X H, et al. Spatial variability of probability distribution of extreme precipitation in Xinjiang[J].ActaGeographicaSinica, 2011, 66(1)： 3-12.

[17] 李计.基于ArchimedeanCopulas函数的多变量干旱频率及空间分析[D]. 杨凌： 西北农林科技大学, 2012.

LI J.MultivariateFrequenciesandSpatialAnalysisofDroughtEventsbasedonArchimedeanCopulasFunctions[D]. Yangling： Northwest A & F University,2012.

[18] 杨好周, 梁忠民, 胡义明,等. 游程理论在云南省干旱重现期分析中的应用[J].水电能源科学, 2013(12)： 8-12.

YANG H Z, LIANG Z M, HU Y M, et al. Application of run-length theory to drought return period analysis of Yunnan province[J].WaterResourcesandPower, 2013(12)： 8-12.

[19] 马秀峰,夏军.游程概率统计原理及其应用[M]. 北京： 科学出版社,2011.

MA X F,XIA J.PrincipleofTravelProbabilityandItsApplication[M]. Beijing： Science Press, 2011.

[20] VICENTE-ERRANO S M, BEGUERA S, LPEZMORENO J I. A multiscalar drought index sensitive to global warming： The standardized precipitation evapotranspiration index[J].JournalofClimate, 2010, 23(7)： 1696-1718.

[21] THORNTHWAITE C W. An approach toward a rational classification of climate[J].GeographicalReview, 1948, 38(1)： 55-94.

[22] 刘永林, 延军平, 岑敏仪. 中国降水非均匀性综合评价[J].地理学报, 2015, 70(3)： 392-406.

LIU Y L, YAN J P, CEN M Y. Comprehensive evaluation of precipitation heterogeneity in China[J].ActaGeographicaSinica, 2015, 70(3)： 392-406.

[23] 韩兰英, 张强, 姚玉璧,等. 近60 a中国西南地区干旱灾害规律与成因[J].地理学报, 2014, 69(5)： 632-639.

HAN L Y,ZHANG Q,YAO Y B,et al. Characteristics and origins of drought disasters in Southwest China in nearly 60 years[J].ActaGeographicaSinica, 2014, 69(5)： 632-639.

[24] 韦小雪, 周渭, 黄远盼,等. 东亚季风对西南地区秋冬春连旱的影响分析[J].安徽农业科学, 2015(28)： 154-156.

WEI X X, ZHOU W, HUANG Y P, et al. The east Asian monsoon impact analysis of the autumn/winter spring drought in southwest [J].JournalofAnhuiAgriculturalSciences, 2015(28)： 154-156.

[25] 宋超辉.东亚和南亚热带夏季风的关系及影响研究[D]. 南京： 南京信息工程大学, 2014.

SONG C H.StudyontheRelationshipbetweentheEastAsiaandSouthAsiaSummerMonsoonandItsInfluence[D]. Nanjing： Nanjing University of Information Science & Technology, 2014.

[26] 左冬冬, 侯威, 颜鹏程,等. 基于游程理论和两变量联合分布的中国西南地区干旱特征研究[J].物理学报, 2014, 63(23)： 45-56.

ZUO D D,HOU W,YAN P C,et al. Research on drought in southwest China based on the theory of run and two-dimensional joint distribution theory[J].ActaPhysicaSinica, 2014, 63(23)： 45-56.