模糊C均值聚类在光伏阵列故障样本数据识别中的应用

陆灵骍，朱红路，连魏魏，戴松元，姚建曦

（华北电力大学可再生能源学院，北京市 昌平区 102206）

0 引言

在全球气候环境日益恶化和化石能源日益枯竭的背景下，大力发展可再生能源已经成为世界各国的共识[1-2]。在政府的大力支持下，我国可再生能源发展迅速，预计到2020年和2030年，非化石能源占一次能源消费比重分别达到 15%和20%左右[3-4]，其中太阳能以其清洁、安全、取之不尽、用之不竭的显著优势，已经成为发展最快的可再生能源。光伏阵列作为光伏(photovoltaic，PV)系统中最为重要的组成部分[5-6]，因复杂的生产工艺和艰苦的工作环境，发生故障难以避免，这将会降低光伏电站的发电效率，减少其服用寿命，甚至造成火灾，引发安全问题[7]。因此，研究光伏阵列直流侧故障的诊断方法具有重要意义。

光伏阵列常见的故障包括短路故障、开路故障、异常老化、阴影遮挡、旁路二极管失效等，故障种类繁多[8]。随着光伏发电装机容量的扩大，近几年来，光伏系统的智能诊断技术越来越受到大家的关注，常用的方法包括人工神经网络[9]、支持向量机[10]、决策树[11]等。该类智能诊断方法主要通过人工利用先验知识划分并标识故障样本，通过训练诊断模型进行故障诊断。但人工筛选故障样本容易出现漏选、错选等现象，而故障样本的选取直接影响诊断模型的判别精度。因此，针对光伏系统直流侧样本数据智能筛选的研究很有必要。

本文提出一种基于模糊 C均值(fuzzy C-means，FCM)聚类的方法对样本数据进行智能筛选。FCM算法是一种基于目标函数模糊划分的柔性聚类算法，其思想是使得被划分到同一类的对象之间相似度最大，而不同簇之间的相似度最小。其迭代中心可以根据预定义的簇数更新与数据点相对应的隶属度值，更容易达到全局最优，因此十分适合用于样本数据的筛选。本文通过分析不同故障条件下光伏阵列的出力特性，提取故障特征向量；基于 FCM 算法良好的模糊处理功能，成功地将数据样本聚类划分；最后，通过实验验证了该方法的有效性和可靠性。

1 光伏阵列典型故障的仿真和分析

1.1 故障模型仿真

因工作环境艰苦恶劣，光伏阵列发生故障难以避免，本文的主要研究对象包括短路故障、开路故障、异常老化故障、阴影故障。但在实际生活中，往往并不允许光伏阵列工作于故障条件，因此有必要进行不同条件下光伏阵列输出特性的建模仿真。为了得到含有正常的、不同故障条件下光伏系统直流侧输出的数据库，基于文献[12]的方法，在Matlab 2015a环境下建立光伏阵列工程仿真模型。该模型共有3条支路，每条支路包含5个光伏组件，仿真模型如图1所示。该模型仅需出产商提供的参数(如表 1所示)，就能在一定度下还原光伏系统在不同条件下的输出特性，满足工程适用的精度。其中，Uoc为开路电压，Isc为短路电流，Um为最大工作点电压，Im为最大工作点电流，Pm为最大工作点功率。

图1 光伏阵列仿真模型Fig. 1 Simulation model of PV array

表1 光伏组件基本参数Tab. 1 Basic parameters of PV module

1.2 故障条件下阵列的电气特性分析

研究了光伏系统4种典型故障下的电气参数分布特征，对开路故障、短路故障、阴影故障、异常老化故障，4种故障条件进行仿真。简单起见，仿真条件均设置为标准测试条件(1000 W/m2，25℃)。通过分析不同故障条件下光伏系统的输出特性，提取故障特征向量。

不同短路故障条件下的I-V、P-V特性曲线如图2所示。当外部激励条件不变时，与正常运行的光伏阵列相比较，随着被短路组件数量的增多，光伏阵列的短路电流、最大工作点电流不变，而开路电压、最大工作点电压、最大功率逐渐下降。因此，光伏阵列的短路故障在电气参数上体现为开路电压、最大工作点电压、最大功率的减少。

不同开路故障条件下的I-V、P-V特性曲线如图3所示。可见，与正常运行的光伏阵列相比较，随着断开支路增多，光伏阵列的短路电流、最大工作点电流、最大功率逐渐下降，但最大工作点电压、开路电压保持不变。因此，开路故障在光伏阵列电气参数上的体现为短路电流、最佳工作点电流、最大功率的下降。

光伏阵列3种不同的异常老化故障下的I-V、P-V特性曲线如图4所示。可见，与正常运行的光伏阵列相比，随着电阻器阻值的增加时，最大功率点到开路电压点连线斜率的绝对值、最大工作点电压和最大功率明显降低，最大工作点电流略微下降，而开路电压、短路电流基本保持不变。因此，光伏阵列异常老化故障在电气参数上的体现为最大工作点电压，最大工作点电流和最大功率的下降。

不同阴影遮挡条件下光伏阵列的输出特性如图5所示。可见，当光伏阵列出现阴影故障时，因被挡组件带负压导致旁路二极管导通，其I-V、P-V曲线均呈现多峰值，阶梯状的特点[13]。从电气参数分布上考虑，开路电压、短路电流基本无变化，但最大工作点电压、最大工作点电流、最大功率随着被挡组件数量的增多、被挡程度的增大而增大。因此，阴影遮挡在电气参数上的体现为最大工作点电压、最大工作点电流、最大功率减少。

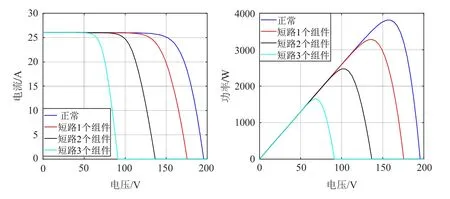
图2 不同短路故障条件下光伏阵列的I-V、P-V特性曲线Fig. 2 I-V and P-V characteristic curves of PV arrays under different short-circuit fault conditions

图3 不同开路故障条件下光伏阵列的I-V、P-V特性曲线Fig. 3 I-V and P-V characteristic curves of PV arrays under different open-circuit fault conditions

图4 不同老化故障条件下光伏阵列的I-V、P-V特性曲线Fig. 4 I-V and P-V characteristic curves of PV arrays under different abnormal aging fault conditions

图5 不同阴影故障条件下光伏阵列的I-V、P-V特性曲线Fig. 5 I-V and P-V characteristic curves of PV arrays under different shading fault conditions

1.3 故障特征提取

光伏阵列I-V、P-V特性曲线不同的非线性畸变，主要反映在 Uoc、Isc、Um、Im等电气特征参数的变化上，如表2所示。因此选取开路电压、短路电流、最佳工作点电压和电流作为故障特征向量，而每种故障均会导致最大功率的减少，故并未选择其作为故障特征向量。

表2 不同故障条件下电气特征参数变化Tab. 2 Variation of electrical characteristic parameters under different fault conditions

1.4 特征向量的标准化转换

即使光伏阵列正常工作，由于所接受的辐照度和温度不断变化，其输出特性也会存在很大差异[14]。 因此，为了消除因辐照度和温度变化而带来的影响，本文提出了如式(1)—(4)所示的转换方法。

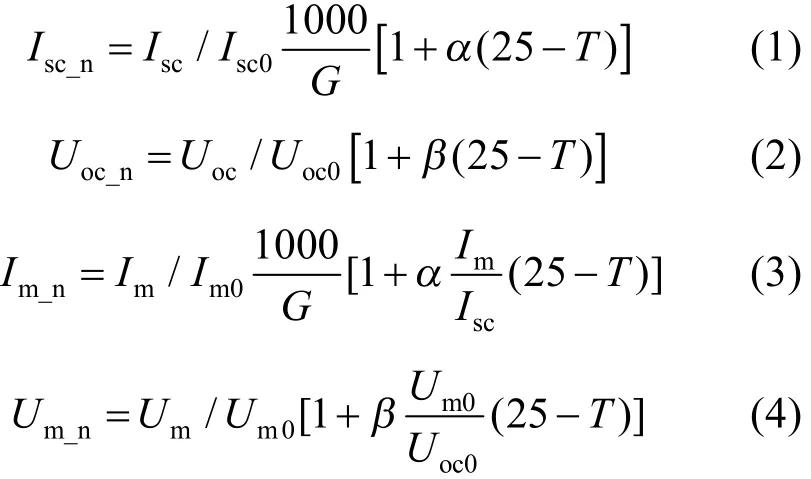
式中：G和T分别为光伏阵列实际接收的辐照度和温度；Uoc0、Um0、Isc0、Im0分别为标准测试条件(standard test condition，STC)下光伏阵列的参数；Uoc_n、Um_n、Isc_n、Im_n分别表示标准化后的参数值。

将特征向量标准化后，所有数据均为0-1之间，仅代表光伏阵列不同故障下的电气特征属性。FCM 算法通过计算欧式距离而使得划分到同一类的数据相似度最大，不同簇之间的相似度最小。因此，标准化故障特征向量可有效解决因外部环境参数变化导致 FCM 算法无法识别故障样本的困难。

2 基于FCM算法的故障样本聚类

模糊C均值聚类算法是一种基于目标函数模糊划分的柔性聚类算法，在模糊聚类应用中最广泛且较为成功。它的思想是使得被划分到同一类的对象之间相似度最大，而不同簇之间的相似度最小。它通过迭代优化目标函数并得到每个样本点对各聚类中心的隶属度，从而决定样本点的类属以达到自动对样本数据进行分类的目的。因此，十分适合用于故障样本数据的智能分类。

设n个数据样本为 X =| xi,i = 1 ,2,3...n |，把 xi分为 C个组类，计算出 C个聚类中心为V={v1,v2, v3,...,vC}，并使得该分类能产生最小的目标函数值，然后计算每个数据点与聚类中心的隶属度。隶属度可以是[0,1]区间内的任意值，它要求一个样本对于各个聚类中心的隶属度总和为 1，即必须满足以下2个原则：

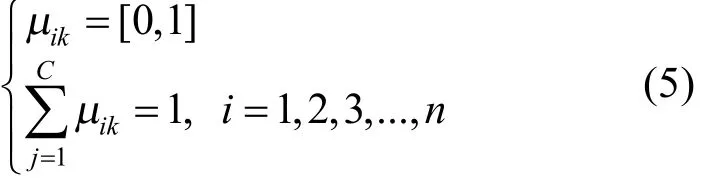
式中：n为样本个数；C为聚类中心个数，即目标分类数；μik为样本xi对于第k类聚类中心的隶属度。

其目标函数Jb一般可表述为

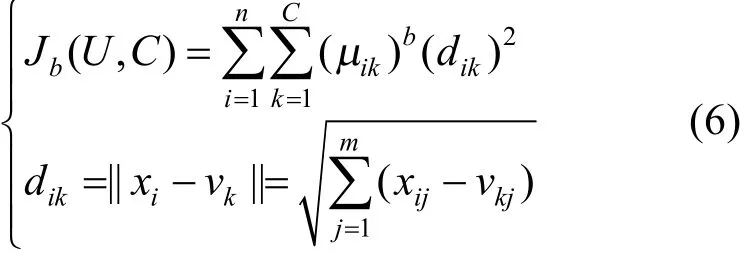
式中：dik为欧式距离，用来度量第i个样本xi与第k类聚类中心的距离；m为样本特征数；b为加权参数，b∈[1,]∞。

使式(6)有最小值的目标函数表达式为

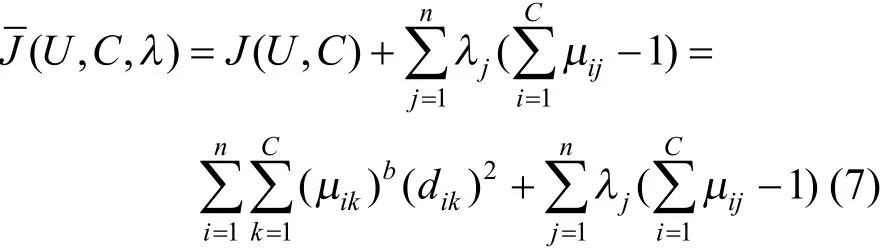
式中λ为拉格朗日乘数。

对所有输入参量求导，使式(6)达到最小值的必要条件为：

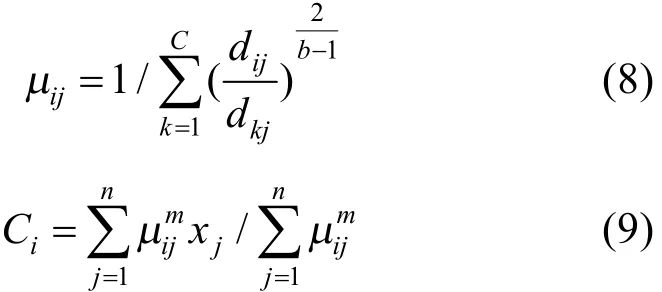
FCM 算法的输出是 C个聚类中心点向量和一个C×n的隶属度矩阵，这个矩阵表示每个样本点属于每个类的隶属度。根据这个矩阵按照模糊集合中的最大隶属原则就能确定每个样本点的分类。相比较于其他聚类算法，FCM具有以下优点：

1）可能会导致不确定性，这有助于在确定边界时产生更适合的结果。

2）计算复杂程度最小。当使用模糊集间隔值时，将进一步减小计算复杂程度。

3）它对初始化相对不敏感。

4）使用模糊规则的数量最少。

5）断点和相似性概念的使用，使得分类更为精确且用时更短。这种量化的相似性概念使得变量的聚类与其他方法相比更有效。

FCM算法流程图如图6所示，默认情况下，ε取值为0.000 01。首先根据样本数据和预分类的故障类别数，计算各类别的聚类中心；然后计算各个数据对于聚类中心的隶属度大小；最后计算目标函数值。如果目标函数的差值ΔJ小于设定的阈值ε，则完成迭代，输出隶属度矩阵。通过比较隶属度的大小，即可完成样本数据的智能筛选。

图6 FCM流程图Fig. 6 FCM algorithm flowchart

3 方法验证

通过仿真数据及实证平台的实际运行数据对提出的故障数据提取方法的有效性进行验证。

3.1 实证平台的搭建

图7 光伏阵列实证平台Fig. 7 Photovoltaic array empirical platform

搭建实证测试平台如图7所示，包括：3×13的光伏阵列，组件基本参数如表1所示；高精度的水平和倾斜面辐照仪；温度传感器；IV扫描仪等。通过该平台，分别对短路、开路、阴影遮挡、异常老化4种不同的故障进行实验研究，并采集阵列运行数据。

表3 各类故障的聚类中心Tab. 3 The cluster centers of different faults

3.2 FCM聚类结果分析

图8 聚类结果误差分析Fig. 8 Error analysis of cluster results

基于第 1.1节和 3.1节建立的仿真和实际运行数据库，通过式(1)—(4)转换后，本节使用FCM算法将样本数据划分为 12类。仿真数据库共有1476组数据，其中每种类型的故障各123组数据；实际运行数据库共有984组数据，其中每种类型的故障各82组数据。通过FCM算法得到12组数据及各组的聚类中心，如表3所示。

聚类使得被划分到同一类的数据相似度最大，而不同簇之间的相似度最小，而每一类数据的聚类中心代表着该类的电气特性。以短路故障为例，从表3可以看出，与正常情况相比，随着短路组件数量的增多，开路电压(仿真结果)由0.936 pu逐渐跌落到0.584 pu，最大工作点电压(仿真结果)由0.861 pu逐渐跌落到0.512 pu。此时，FCM算法能够有效的识别出此类故障数据。

仿真数据聚类结果的分类模糊矩阵如图 8(a)所示，红色和绿色的子矩阵分别表示分类错误和正确的样本数量。例如，目标分类为‘1’的样本的数量为123个，占总样本的8.3%。基于FCM算法聚类后，实际分类为‘1’的样本数为123个，正确率为100%。同理，目标分类为2、3、4、5、6、11、12的样本经FCM算法聚类后，分类正确均为 100%。可以看到，错误聚类主要发生于目标分类为7、8、9、10之间。有6个原属于类别7的样本却被错误的分到了类别 9，正确率为95.1%；有7个原属于类别8的样本却被分到了类别9，正确率为94.3%；最后有4个原属于类别10的样本被分到了类别7，正确率为96.7%。右下角蓝色的子矩阵表示算法整体的正确率和错误率分别为98.8%和1.2%。

实际运行数据的聚类结果如图8(b)所示，算法的聚类正确率为 97.2%。样本错误聚类主要发生于目标分类为 7、8、9、10、11、12，即阴影故障和异常老化故障之间，其主要是因为该2种故障均影响光伏阵列的最大工作点电压和最大工作点电流。

4 结论

针对从光伏阵列的运行数据中有效提取故障样本的问题，提出了基于模糊C均值聚类算法对样本数据智能聚类的方法，通过仿真和实验得到以下结论：

1）不同的故障条件对光伏阵列的输出特性有不同的影响。开路故障主要影响光伏阵列的短路电流、最大工作点电流；短路故障主要影响光伏阵列的开路电压、最大工作点电压；阴影故障和异常老化故障主要影响光伏阵列的最大工作点电流、电压。

2）标准化故障特征向量，能有效解决因外部环境参数变化而导致 FCM 算法无法有效识别样本数据的困难。

3）该方法能简单、快速、高效的对样本数据进行聚类划分，为后期光伏阵列的故障诊断提供技术支持。

[1] 孔德同，贾思远，王天品，等．基于振动分析的风力发电机故障诊断方法[J]．发电与空调，2017，38(1)：54-58．

[2] 张钟平，宣施超．分布式光伏设计要点分析[J]．发电与空调，2015(1)：10-13．

[3] 国务院办公厅．能源发展战略行动计划(2014-2020年)(摘录)[J]．上海节能，2014(12)：1-2．

[4] 刘保松，刘晓光，刘庆超．现行条件下我国光伏发电盈利分析[J]．发电与空调，2015(1)：43-45．

[5] Madeti S R，Singh S N．Online fault detection and the economic analysis of grid-connected photovoltaic systems[J]．Energy，2017，134(1)：121-135．

[6] 唐治平，周璐，魏超．光伏电站智能清洗模型及实例分析[J]．发电与空调，2015(1)：25-29．

[7] Triki-Lahiani A，Abdelghani B B，Slama-Belkhodja I．Fault detection and monitoring systems for photovoltaic installations：A review[J]．Renewable &Sustainable Energy Reviews，2017，82(3): 2680-2692.

[8] Hazra A，Das S，Basu M．An efficient fault diagnosis method for PV systems following string current[J]．Journal of Cleaner Production，2017，154(15)：220-232．

[9] 王元章，李智华，吴春华，等．基于BP神经网络的光伏组件在线故障诊断[J]．电网技术，2013，37(8)：2094-2100．

[10] Yi Z，Etemadi A H．A novel detection algorithm for Line-to-Line faults in Photovoltaic (PV) arrays based on support vector machine (SVM)[C]//Power and Energy Society General Meeting，Boston，MA，USA，2016：1-4．

[11] Zhao Y，Yang L，Lehman B，et al．Decision tree-based fault detection and classification in solar photovoltaic arrays[C]//Applied Power Electronics Conference and Exposition，Orlando，FL，USA，2012：93-99．

[12] 傅望，周林，郭珂，等．光伏电池工程用数学模型研究[J]．电工技术学报，2011，26(10)：211-216．

[13] Youssef A，El-Telbany M，Zekry A．The role of artificial intelligence in photo-voltaic systems design and control：A review[J]．Renewable & Sustainable Energy Reviews，2017，78(10)：72-79．

[14] 钟天宇，刘庆超，杨明．并网光伏电站光伏组件支架最佳倾角设计研究[J]．发电与空调，2013，34(1)：5-7．

陆灵骍